今回の記事では通過算をトピックとして扱うシリーズの2本目として,受験問題を引用しながら応用的な解答法・攻略法についてご紹介していきます。通過算という文章題は,道のり・速さ・時間という受験生が苦手としがちな要素が登場するだけあって,多くの人がつまずきやすい単元です。しかし,その分しっかり理解しておくだけで大きな得点源になるでしょう。よろしければ一読してみてください。
Contents
基礎編の復習!通過算とは?
それでは最初は基礎編でお教えしたことの復習といきましょう。そもそも通過算とは,あるものがあるものを通過するというシチュエーションにおける文章題のことを指しました。そのため道のり・速さ・時間といった要素が必ず登場してくるわけです。
そんな通過算ですが,出題形式には3つのパターンが存在しましたね。そのうち1つ目は止まっているモノを通り過ぎる通過算,2つ目は動いているモノを追い越す通過算,3つ目は動いているモノがすれ違う通過算になります。それぞれのパターンについて若干攻略法や図の書き方・注目する要素などが異なりますが,基本的な攻略法は同じです。その手順とは答えとなっている要素から逆算して必要な情報を洗い出し,電車の先頭がどこからどこまで動いたかを考えて道のり・速さ・時間を求めていき,単位に気をつけながら計算を進めていく,というものでした。詳しくは基礎編に書いていますのでそちらをご参照ください。今回の記事ではこれらの攻略法に基づいて,受験問題の解き方をご紹介していきます。
問題① パターンを見分けよう!基本的な通過算
基本編で確認したことを振り返ったところで,本題の問題演習に移りましょう。まずはありきたりな通過算の問題をご紹介いたします。この問題がどのパターンに該当するのかなどを慎重に考えながら,ウォーミングアップがてら解き進めてみましょう。
長さ84mの電車が,長さ312mの鉄橋を渡り始めてから,渡り終わるまでに24秒かかりました。この電車の速さは,時速何kmですか。
(東京学芸大学附属竹早中学校(2014),一部改題)
解説①
いかがでしたでしょうか。ここからは解説に移りたいと思います。問題の攻略法は基本編で既にお教えしていますので,その手順に沿って一緒に確認していきましょう。まず大切なことがパターンの判別や答えとして求められている要素の確認です。今回は「電車」という動いているモノが鉄橋という動かないモノの上を通過しているので,パターンとしては1つ目の止まっているモノを通り過ぎる通過算になりますね。そして今回は電車の速さが求められているので,電車がどれくらいの道のりをどれくらいの時間で走っていたのかを計測すれば無事答えが導かれそうです。なお今回は渡り終わるまでにかかった時間が24秒と与えられているので,電車が何m走ったのかを考えていきましょう。
ここで引っかかりがちなのが,道のり=鉄橋の長さだと勘違いしてしまうことです。電車が鉄橋を渡ったと言われるとついそのように考えてしまいますが,渡り始め・渡り終わりの意味に注目すると何がいけないのかが見えてくるかと思われます。ここでの渡り始めとは電車の先頭が鉄橋に差し掛かったときであり,渡り終わりとは電車のお尻が鉄橋から出たときを指します。つまり渡り終わるまでに電車が走った距離は鉄橋の距離よりも長くなってしまうのです。それでは電車は一体どれくらいの距離を走ったのでしょうか。先程ご説明した「渡り始め・渡り終わり」の定義に基づくと,電車の走った距離は次のように図示できます。
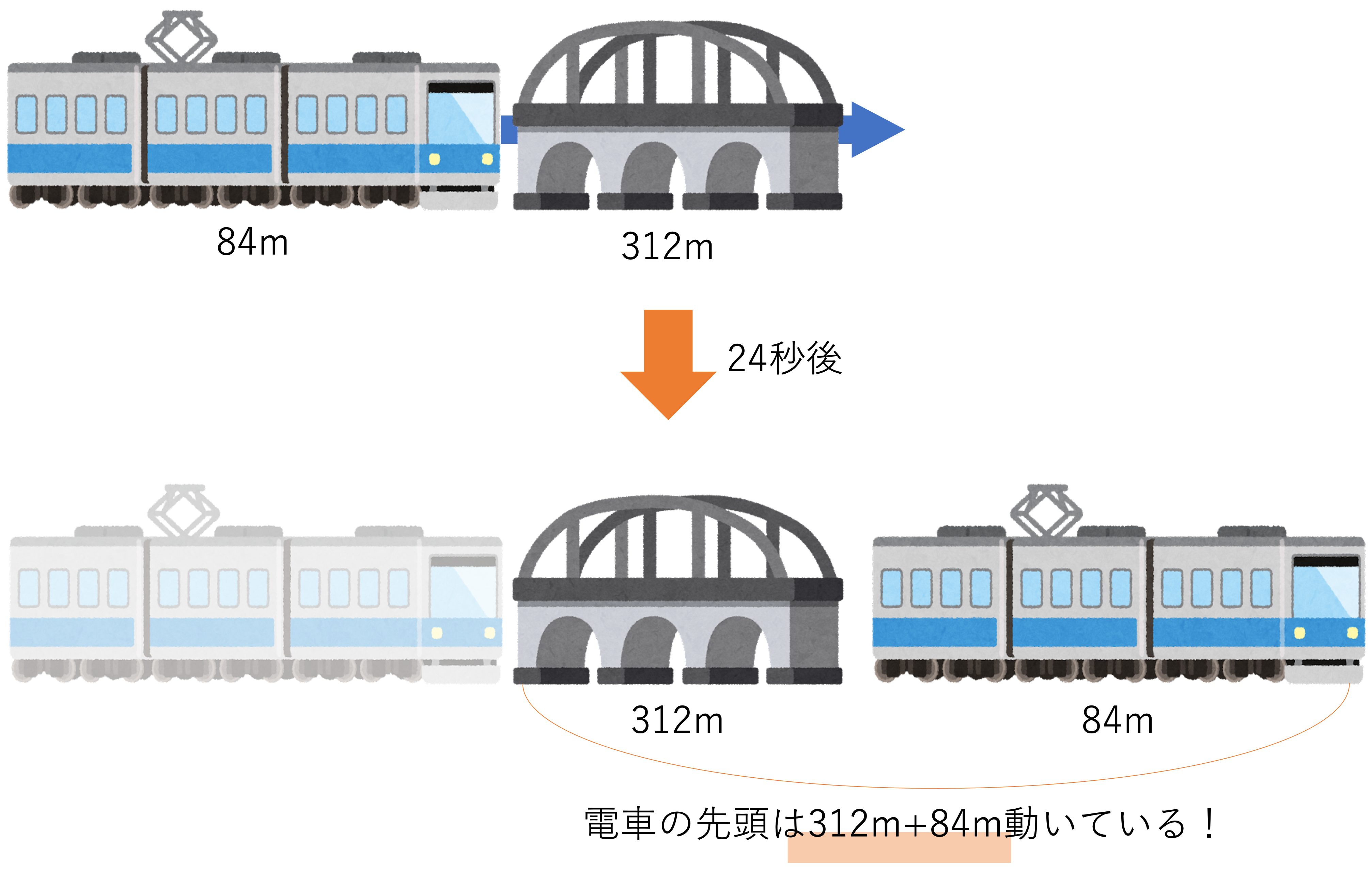
この図から,電車は鉄橋の長さ+電車自身の自身の長さを走ったことがわかります。ここでは鉄橋が312m,電車の長さが84mだったので,合計で396m走っていることになります。このように正確に道のりを計算するために電車の先頭が動いた距離に注目する必要があるのですね。さて,ここで電車の進んだ道のりと時間が分かったので無事速さを計算できそうです。今回問われている単位は時速□kmなので,その形に単位を揃えることを意識して進めていくことを忘れずに考えると,下のような答えが導かれます。mをkmに直すときは1000で割る,秒を分に・分を時間に直すときは60で割る,といったテクニックを思い出しながら計算してみましょう。
396[m]÷24[秒]=速さ[秒速・m]
(396÷1000 [km])÷(24÷60÷60[時間])=59.4[時速・km]
A.時速59.4km
問題② 比が登場する通過算!
続いては比が登場する通過算について扱っていきたいと思います。道のり・速さ・時間が直接与えられない分,計算がやや複雑になるかと思われますが,基本の解き方を抑えておけば無事解くことができるかと思われます。
次の□にあてはまる数を答えなさい。
長さ160mの普通列車を,長さ200mの特急列車が追いついてから追いこすまでに24秒かかります。普通列車と特急列車の速さの比が6:11のとき,特急列車の速さは毎秒□mです。
(法政大学中学校(2016),一部改題)
解説②
ここからは解説に移ります。まずは1問目と同様に,問題文の整理や分析を行なっていきましょう。この問題でも「列車」という動くモノが登場していますが,今回注目すべき点は2つの電車が登場しているということです。そして特急列車が普通列車を追い越すということは,基本編で触れたパターンの2つ目である動いているモノが動いているモノを追い越す場合の問題に当てはまりますね。そのため,パターン②の攻略法を思い出しながら進めてみましょう。またこの問題では特急列車の速さが求められています。そのため特急列車の動いた道のりや速さを考えていけば答えに辿り着けそうだと予想が立てられますが,それと同時に普通列車の長さや進む速さのことも忘れずに考えていきましょう。ここで普通列車の速さを秒速○m・特急列車の速さを秒速□mとすると,問題の情報は次のような図にまとめられます。
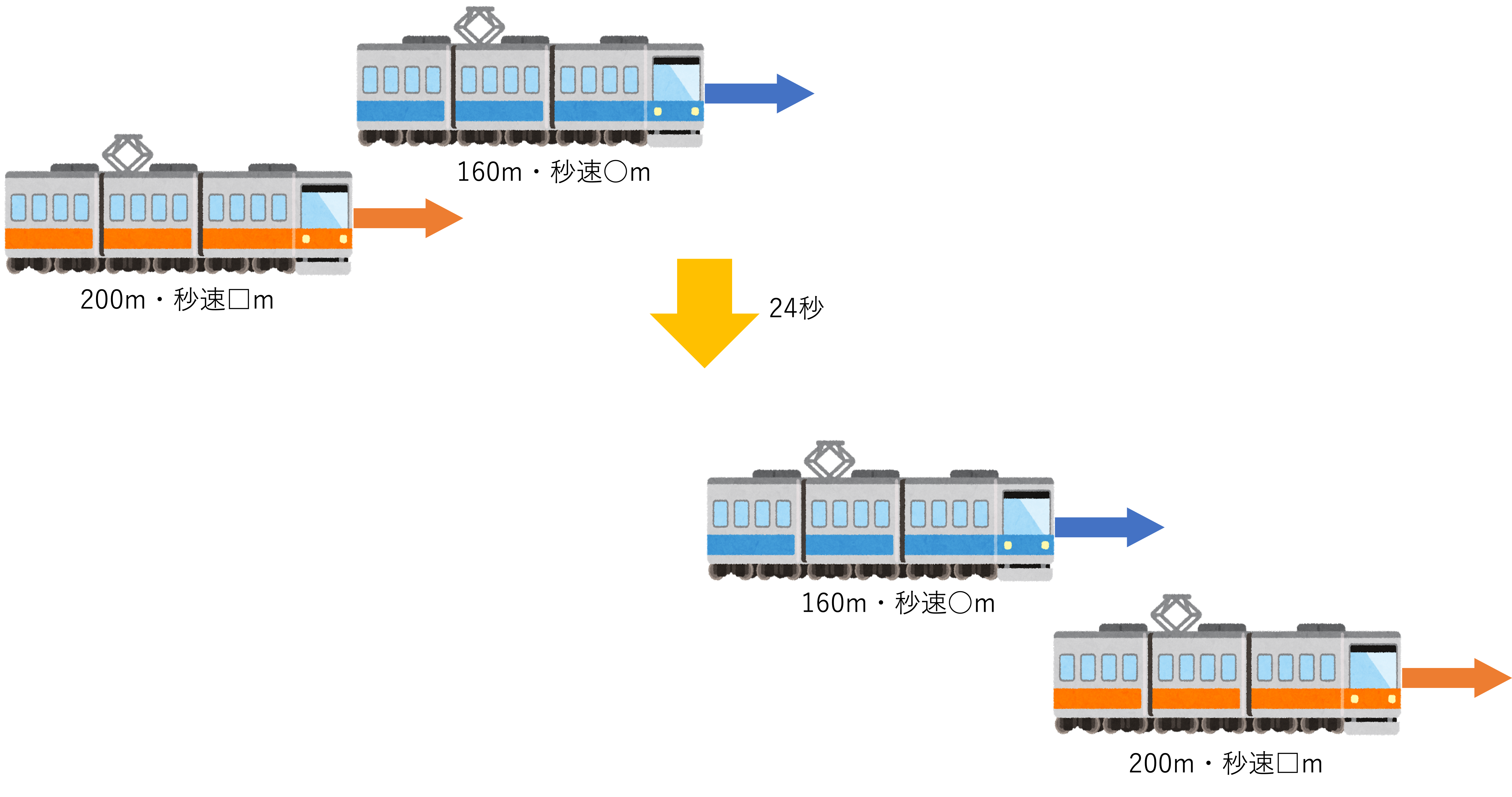
この図から分かることは,2つの列車は24秒をかけて距離を縮めて追い抜いていったということです。そして列車の走る速さが一定である以上,2つの列車の距離は一定のスピードで変化していくことになります。いま普通列車の速さが秒速○m・特急列車の走る速さが秒速□mと設定したので,ここでは1秒間につき距離が□-○[m]変化していくと判断できます。
次に進んだ道のりについて考えましょう。今回の問題では2つのモノが両方動いているので,どこからどこまで走ったかを正確に計算することはできません。しかし,特急列車の先頭が普通列車のお尻に接しる状態から特急列車のお尻が普通列車の先頭に接する状態まで,要するに特急列車が普通列車よりも普通列車の長さ+特急列車自身の長さ分多く走ることができればいいわけです。そして今回の問題ではそもそも動きの差について考えてきました。つまり列車それ自体ではなく,「ズレ」がどれくらい動いているのか・どれくらいのスパンで生じているのかを見てきたわけです。このことから道のりも,相対的な距離のことを指すと思って計算してしまいましょう。
加えて本問題では,特急列車が普通列車のことを24秒で追い越したという呪法が与えられています。したがって次のような式が成立することがわかり,このことから1秒間に2つの列車の距離は15mずつ変化していくということがわかります。
(□-○)[秒速・m]×24[秒]=360[m]
(□-○)[秒速・m]=15
ここで今回は普通列車の速さを秒速○m・特急列車の速さを秒速□mとおいて計算を進めてきたことに立ち返りましょう。問題文を改めて確認すると,普通列車と特急列車の速さの比は6:11であることがわかります。そのため△という記号を使うと速さの比は次の世に書き換えられるのです。
普通列車の速さ:特急列車の速さ=○:□=6:11=6×△:11×△
そしていま2つの列車の速さの差である□-○[秒速・m]の値が15であることから,△の値は次のように求められ,単位に注意して回答すると答えとなる特急列車の速さは秒速33mであると導かれます。
11×△-6×△=15
5×△=15
△=3
特急列車の速さ=11×△=33[秒速・m]
A.秒速33m
問題③ 2つのパターンが関係する通過算!
続いてチャレンジしていただくのは,問題②と同様少し複雑な文章題です。複雑といっても今回は計算が難しいのではなく,問題文の中身の整理に手間取ってしまうかもしれません。パターンがどうであろうと,攻略の基本は問題の分析・先頭への注目・単位の変換の3点です。その辺りを意識しながら解いてみましょう。
長さ216mの快速列車と長さ126mの普通列車がすれちがうとき,出会ってからはなれるまでに9秒かかります。また,この快速列車と普通列車が同じ向きに進むとき,快速列車が普通列車に追いついてから追いこすまで57秒かかります。
このとき,快速列車は時速何kmですか。
(明治大学付属中野中学校(2015),一部改題)
解説③
それではここからは解説に移ります。まずは攻略の手順にしたがって問題の整理・分析から始めていきたいのですが,今回は快速列車・普通列車という2つの動くモノが登場していました。しかしここで重要なのが追い越しとすれ違い,つまり2つの出題パターンが結び付けられて出題されているということです。そのためこれまでと勝手が違うかもしれませんが,まずは図などに情報を整理して,内容をきちんと把握することに努めましょう。
また今回の問題は快速列車の速さを問うものでした。そのため道のりと時間が分かれば無事解けそうですね。ここでは普通列車の速さを秒速○m・快速列車の速さを秒速□mと設定して,計算を進めていきましょう。なお秒速・mで単位を定めたのは,与えられている電車の長さ(m)や進んだ時間(秒)と数値を合わせるためです。このように柔軟に単位を定めて計算を簡単にすることを意識して進めてみるといいでしょう。以上の事柄をまとめると,下のような図に整理できます。
あとはこの図のそれぞれの場合について道のり・速さ・時間に関する式を立てていけば,□と○の関係を明らかにすることができ,答えに辿り着くことができそうです。まずは左側の追い越すときの場合ですが,こちらは先程解いた2問目の問題と同じように進めてみましょう。ここでの速さとは列車それ自体の速さではなく差異の変化の速さ,つまりはどれくらいのスピードで列車間の距離が変化するかということです。今回の問題では快速列車が秒速□m・普通列車が秒速○mだったので,追い越しが発生するとき2つの列車は1秒間に□-○[m]ずつ変化していくことになります。また次は道のりに関してですが,こちらも2問目で触れたように,快速列車が普通列車より普通列車の長さ+快速列車自身の長さ分,つまりは216[m]+126[m]=342[m]多く走れば指示通り追い越すことができますね。今回の問題ではズレ・差異がどれくらいの期間・距離・速さで発生するのかを確認していくことが大切なので,なかなか理解しがたいところもあるでしょうが,少しずつ慣れてきましょう。これらのこと及び文中で登場した時間をまとめると下のような計算式が出来上がります。
(□-○)[秒速・m]×57[秒]=342[m]
□-○[秒速・m]=6
次は右側のすれ違いについての場合について確認していきましょう。こちらは前回の基礎編で紹介したパターン③に該当するシチュエーションですね。このような問題でも大切なことは列車同士の差異やズレに注目することです。まずは列車の距離の差異の変化に注目してみましょう。快速列車が秒速□m・普通列車が秒速○mで走るとき,そしてそれらが別々の向きに進んでいるとき,2つの列車の距離は1秒間に□+○[m]ずつ変化していくことが分かります。また道のりについては,こちらも分かりにくくはありますが,快速列車と普通列車の先頭と先頭が重なってから快速列車と普通列車のお尻とお尻が重なるまでの距離を指すことから,その大きさは普通列車の長さ+快速列車自身の長さ分,つまりは342mになると判断できます。この道のりの求め方は実はパターン②と③とで全く同じです。動いているモノ同士の通過算における距離とは全長の総和なのだと覚えてしまうといいでしょう。これらのことに文中で登場した時間の要素を組み合わせると,下のような式が完成します。
(□+○)[秒速・m]×9[秒]=342[m]
□+○[秒速・m]=38
以上の2つの計算式から,快速列車の速さである□と普通列車の速さである○の関係が見えてきましたね。□と○は足すと38・引くと6になる2つの数字のことを指します。そしてこの条件を満たす数字は22と16のペアしかありません。このことから快速列車は秒速22mで,普通列車は秒速16mで進むことが分かりました。ここで今回聞かれているのは快速列車の時速だったので,あとは秒速22mという値を問題文で聞かれている形に変化させていけば,正しい答えに辿り着けそうです。このとき単位をきちんと揃えてあげることを忘れずに計算を進めていくと,下のような回答が得られます。
快速列車の速さ[時速・km]=22[秒速・m]×60×60÷1000=79.2[時速・km]
A.時速79.2km
問題④
ここからは入試問題の中でも難しめなものの演習に移ります。計算や図表がややこしくなるので,その分情報の整理にゆっくりとりかかることを意識して進めてみましょう。
長さ3609mのトンネルの何mか先に長さ306mの鉄橋があります。
いま,長さ81mの電車の先頭がトンネルに入ってから,鉄橋を渡り始めるまでに4分4秒かかりました。また,電車の先頭がトンネルを出た時から,電車が完全に鉄橋を渡り終えるまでに1分41秒かかりました。次の問いに答えなさい。
(1)この電車の速さは,時速何kmか求めなさい。
(2)トンネルの出口から鉄橋までの距離は何mか求めなさい。
(城北中学校(2009),一部改題)
解説④
では解説に移りましょう。まずは大前提として,今回の問題では電車という動くモノが鉄橋・トンネルという動かないモノを通り越すときの計算でした。つまりパターン①に該当することになりますね。通常であればこのことを踏まえて攻略法の通り,求められているものの確認・先頭が動いた距離の計算などと進めていくのですが,今回はトンネルと鉄橋の両方を渡ることから少々勝手が違います。そのためいつも以上に正確に図にまとめることを意識してみるといいでしょう。トンネルと鉄橋の間の距離を□mとし,この問題で与えられている要素をまとめると,次の図のように情報を整理できます。
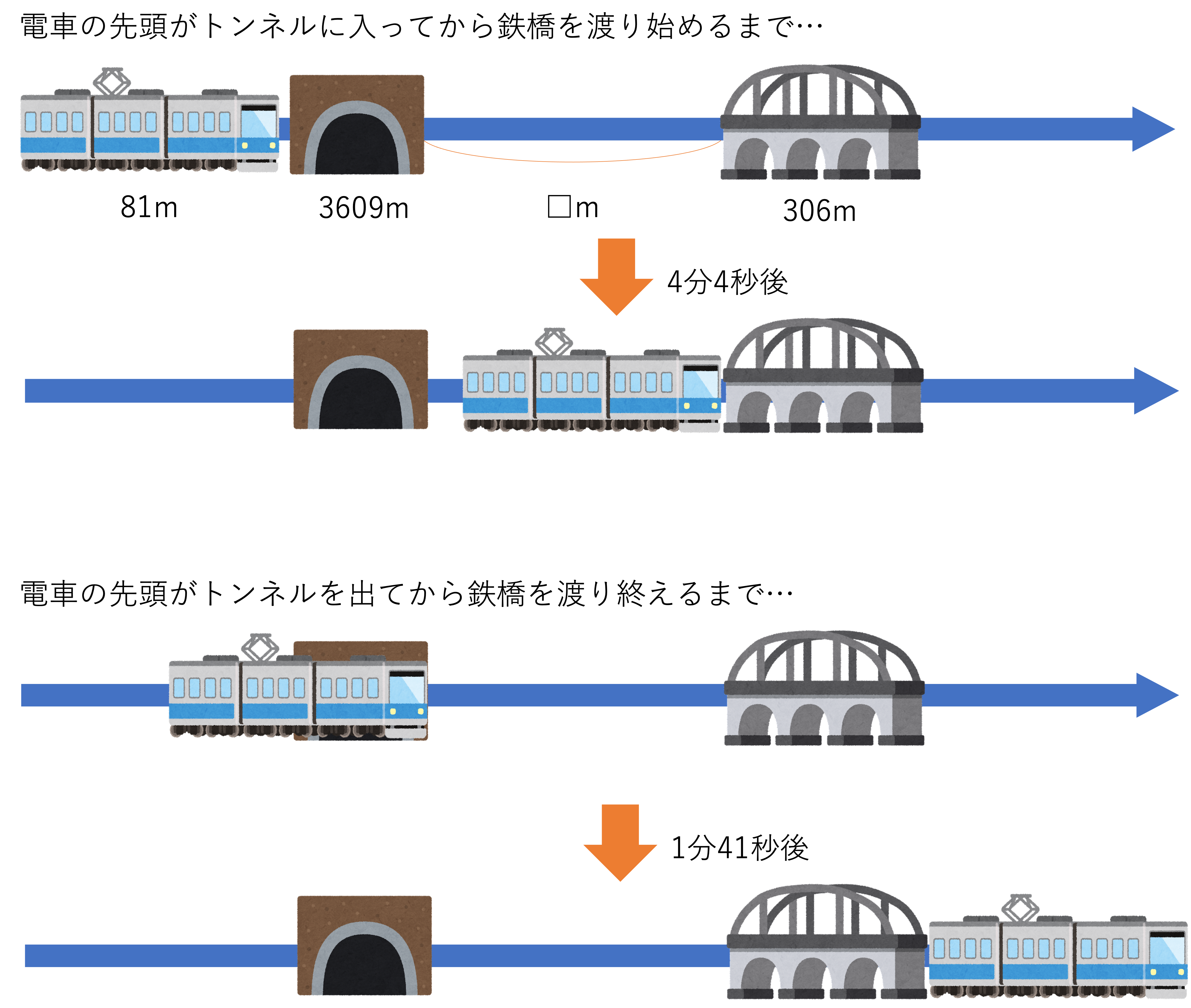
このような図を書くことすら難しく感じてしまうような問題ですが,3問目と同じようにそれぞれの場合をじっくり考えれば答えに辿り着くことができます。中学受験の算数で大切なことは予想をつけながらもとりあえず手を動かすということです。頭で考えても分からないことが,図表や計算式の形になるとすんなり理解できたりするものです。
今回の問題でも上の場合から順番に考えていきましょう。まず先頭がトンネルに入ってから鉄橋を渡り始めるまでに関してですが,このとき電車が走った道のりはどれくらいでしょうか。電車はトンネル及びトンネルと鉄橋の間にある線路を通っているので3609+□[m]進んだことになります。このときかかった時間が4分40秒=280秒でした。
他方下の場合,電車の先頭がトンネルを抜けてから鉄橋を通り抜けるまでに関してですが,こちらにおける道のりは,電車の先頭が動いた距離に気をつけて計算すると,トンネルと鉄橋の間の線路の長さ・鉄橋の長さ・電車自身の長さを足したものになります。そのため道のりは□+306+81=387+□[m]になりますね。このときかかった時間が1分41秒=101秒でした。
以上のことから,これらの道のりと時間の差を計算することで,電車が何秒で何m進んだかというのを□を使わずに表すことができるようになります。上の場合と下の場合とでは道のりに(3609+□)-(387+□)=3222[m]の差があり,時間に280-101=179[秒]の差があります。このことから電車の速さは次のように計算できます。このとき,今回は電車が1時間に何m進むかが聞かれていることに注意して単位をきちんと揃えましょう。
3222[m]÷179[秒]=18[秒速・m]
18[秒速・m]×60×60÷1000=64.8[時速・km]
A.(1)時速64.8km
続いてここで計算したことを活かしてトンネルと鉄橋の間の距離を求めましょう。ここで再び図の下の場合,つまりは電車の先頭がトンネルを抜けてから鉄橋を通り抜けるまでの場合を考えていきましょう。上の場合にしなかったのは,道のりは4けたの数字であり,計算に時間がかかりそうだからです。些細なところでも計算を簡単にしていく工夫を重ねていきましょう。この場合における道のり・時間・速さをまとめると下の式が出来あがります。なお先ほど時速に変換した電車の速さですが,ここでは速さが秒・道のりがmで登場しているので,秒速18mのまま使ってあげましょう。
道のり=速さ×時間
387+□[m]=18[秒速・m]×101[秒]
この式は□と数字とで構成されています。そのため上の計算式を解いていけば□の中身であるトンネルと鉄橋の間の距離が求められそうです。かけ算や引き算を間違えてしまうといったケアレスミスに注意して計算していくと,以下のような答えが導かれます。
387+□[m]=18[秒速・m]×101[秒]
387+□[m]=1818[m]
□=1431[m]
A.(2)1431m
終わりに
本記事ではこれまで受験問題を引用しながら,通過算の攻略法についてご紹介していきました。ここで取り上げた問題は一部のものに過ぎませんが,大体の通過算は記事中で引用した程度の難易度の問題ばかりです。そのため,よろしければ何度も読み直したり解き直したりして,受験本番でしくじらないように学力を伸ばしていきましょう。おすすめ記事や参考書籍でも通過算について学ぶことができますので,そちらも是非ご参照ください。本記事は今後の学習のお役に立てば幸いです。