今回は集合算について取り扱う記事の2本目である応用編です。基礎編で覚えた考え方や問題の解き方をベースに,応用力を養うことを狙いとした記事になっています。そのため「集合算って何?」という初見の方は前の記事を参考にしてください。集合算は意外と受験でも登場しやすいので,ぜひ引用する問題を解きながら学力を伸ばしていきましょう。
Contents
集合とは?
ではまずは問題に取り掛かる前に,集合算の基本について軽くおさらいしておきましょう。詳しくは前回の記事をご覧頂ければ幸いです。
はじめに,集合というのは何かしらの特徴を持った数字のグループのことを意味しましたね。整数とか小数とか,あるいは偶数や奇数といった具合に,数字はグループを作ることができます。そしてこの集合が2つ以上登場し,片方に属するもの・両方に属するもの・両方に属さないもの,といったような事柄を考えていくのが集合算というものです。
集合算には2種類の解き方がありました。それが,表を作る解き方とベン図を作る解き方ですね。それぞれどんなものかは基礎編の記事で触れているのですが,今回もこのどちらかの解き方で解いていけば,基本的にはきちんとした回答にたどり着けるでしょう。
今回の問題は全てベン図を作って進めていきますが,それをなぞって解いてみるのも表を作るやり方で解いてみるのもいい勉強になるでしょう。
問題① まずは典型問題!
まずは肩慣らしに,前回の例題のような典型的な問題を解いていくことにしましょう。とはいってもこれも入試問題からの引用ですので,本番のような心持ちで考えていけるといいでしょう。
次の□にあてはまる数を答えなさい。
45人のクラスで,通学で利用する交通機関を調べました。電車を利用する生徒は22人,バスを利用する生徒は□人でした。電車もバスも利用しない生徒は,少なくとも5人いることになります。
(鎌倉学園中学校(2018),一部改題)
解説①
それでは解説に移ります。前述したように,この問題では復習の意味も込めてベン図での解き方をご紹介します。まずは全体を表す大きな長方形と,各グループを示す円2つを描いて,問題文で与えられている人数を書き表しましょう。条件を図に起こすと,次のようなベン図に整理できます。
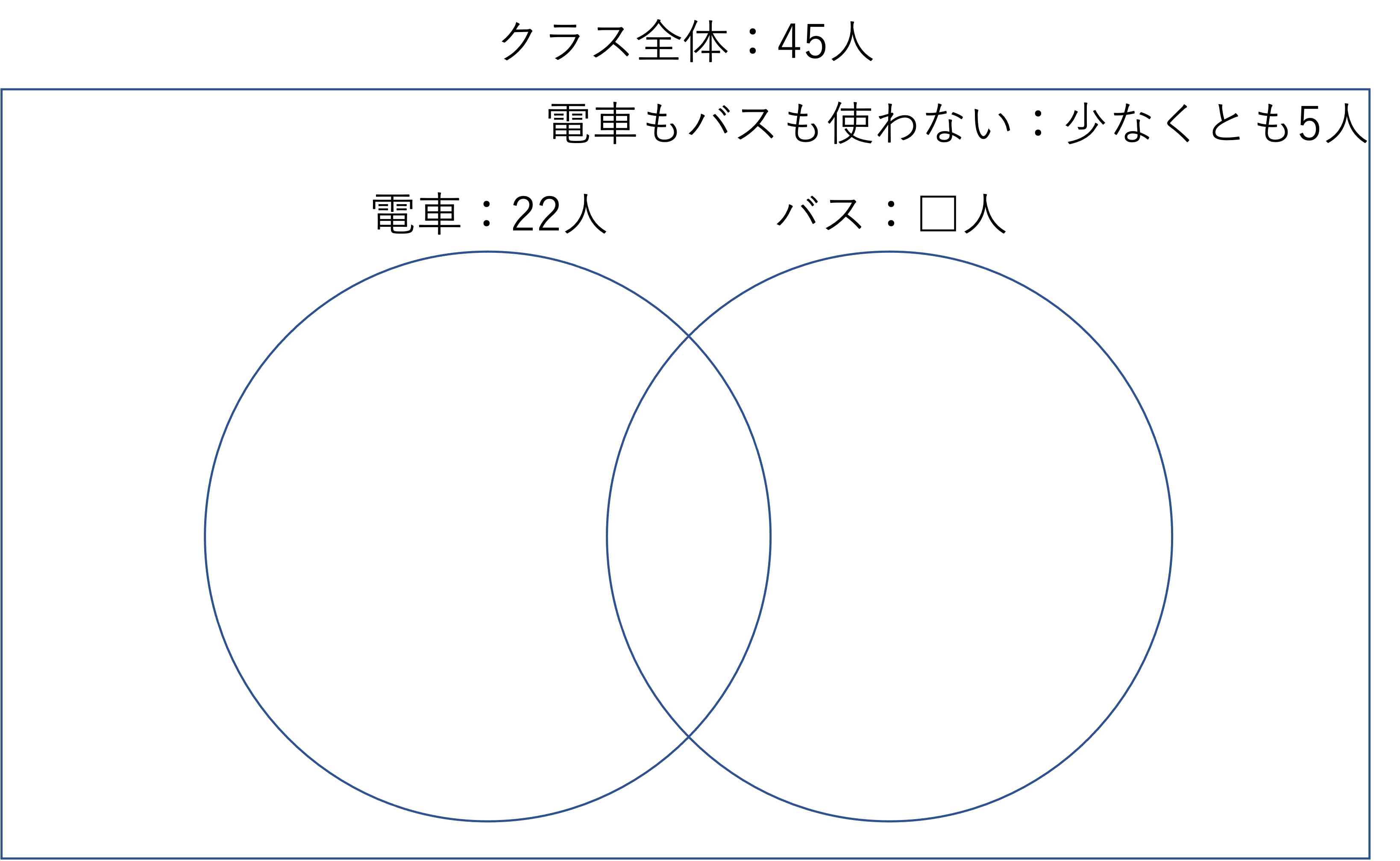
ここまで書くことが集合算の第一ステップです。あとは問題文で聞かれていることを考えていけばいいのですが,今回はバスに乗る人の数が求められているので,そのことについて検討していきましょう。
ここで注目するのが,電車にもバスにも乗らない人が少なくとも5人いるということです。これは裏を返せば,電車またはバス,もしくはその両方に乗る人が最大で40人いるということですね。
いま電車に乗る人は22人です。ここで電車に乗る人の内訳は,①電車には乗るけどバスには乗らない人,②電車にもバスにも乗る人に分けられます。おなじようにバスに乗る人についても,②電車にもバスにも乗る人,③バスには乗るけど電車には乗らない人に分けられます。
今回の問題でこの内訳は明らかになっていませんが,「電車またはバス,もしくはその両方の乗る人」が最大になるのは,②電車にもバスにも乗らない人が0人のときですね。
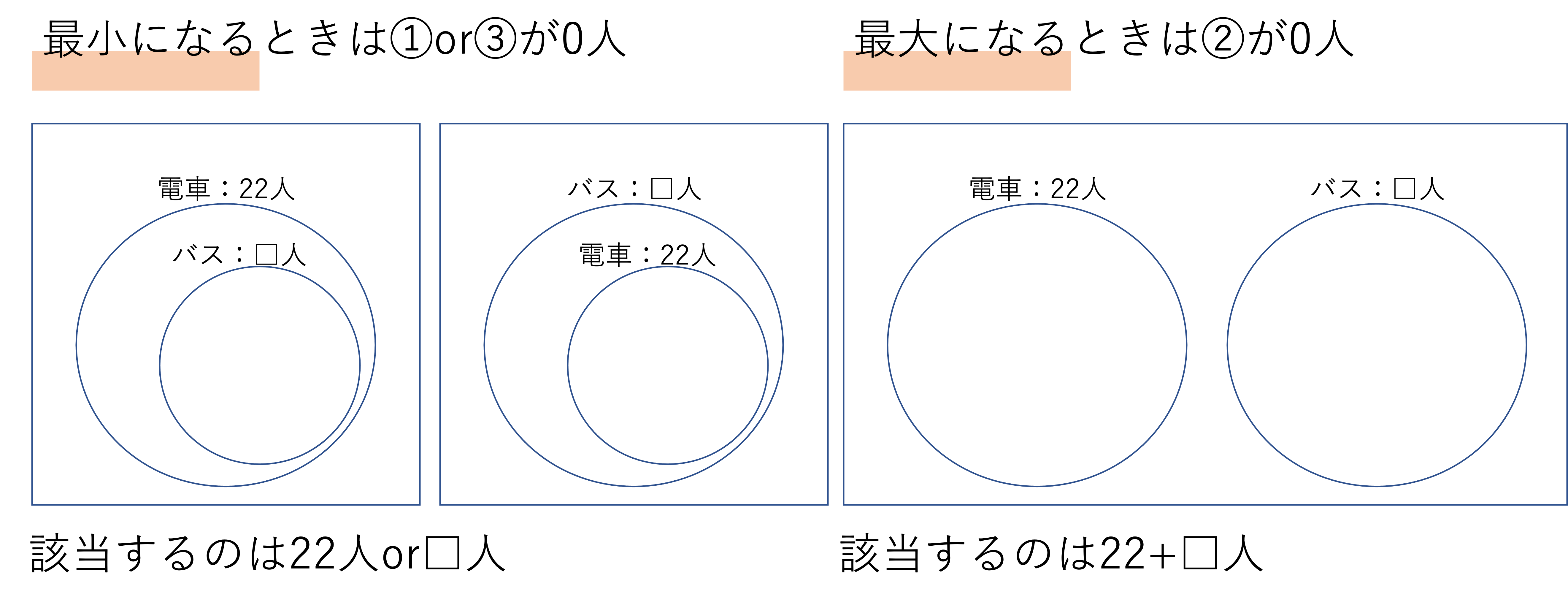
そのため「電車またはバス,もしくはその両方の乗る人」の合計は22+□人になるということです。ここで,このグループに属さない「電車にもバスにも乗らない人」が少なくとも5人以上いるということでしたから,右の最大の場合の図において,2つの円の外側には5人が存在するということがわかります。そのため,45-(22+□)=5という式が成立し,これを解くと答えは18人だと導けます。
A.18人
このようにベン図には,円を動かしたり重ねたりすることで2つのグループの関係をいじれる,という長所があります。最大最小・以下以上という単語に馴染みのない人もいるかもしれませんが,いくつも図を作りながら丁寧に解いていきましょう。
問題② 以下・以上が絡んでくる集合算!
それでは続いて以下・以上が絡む集合算を解いていきます。先程の問題でも「少なくとも」といった語句が出ましたが,こちらの問題の方がやや難しいかと思われます。それでも気合を入れてチャレンジしてみましょう。
40人の生徒にサッカー,テニスが好きかどうか聞いたところ,サッカーが好きだと答えた生徒は32人,テニスが好きだと答えた生徒は26人でした。どちらも好きではない生徒は,何人以下ですか。
(田園調布学園中等部(2015),一部改題)
解説②
ここからは答え合わせに移ります。やや難しい,とは言いましたがこの問題②も典型的な集合算です。まずは今回の問題で登場した,サッカーが好きかどうか・テニスが好きかどうかに関する人の数をベン図に書き起こしましょう。
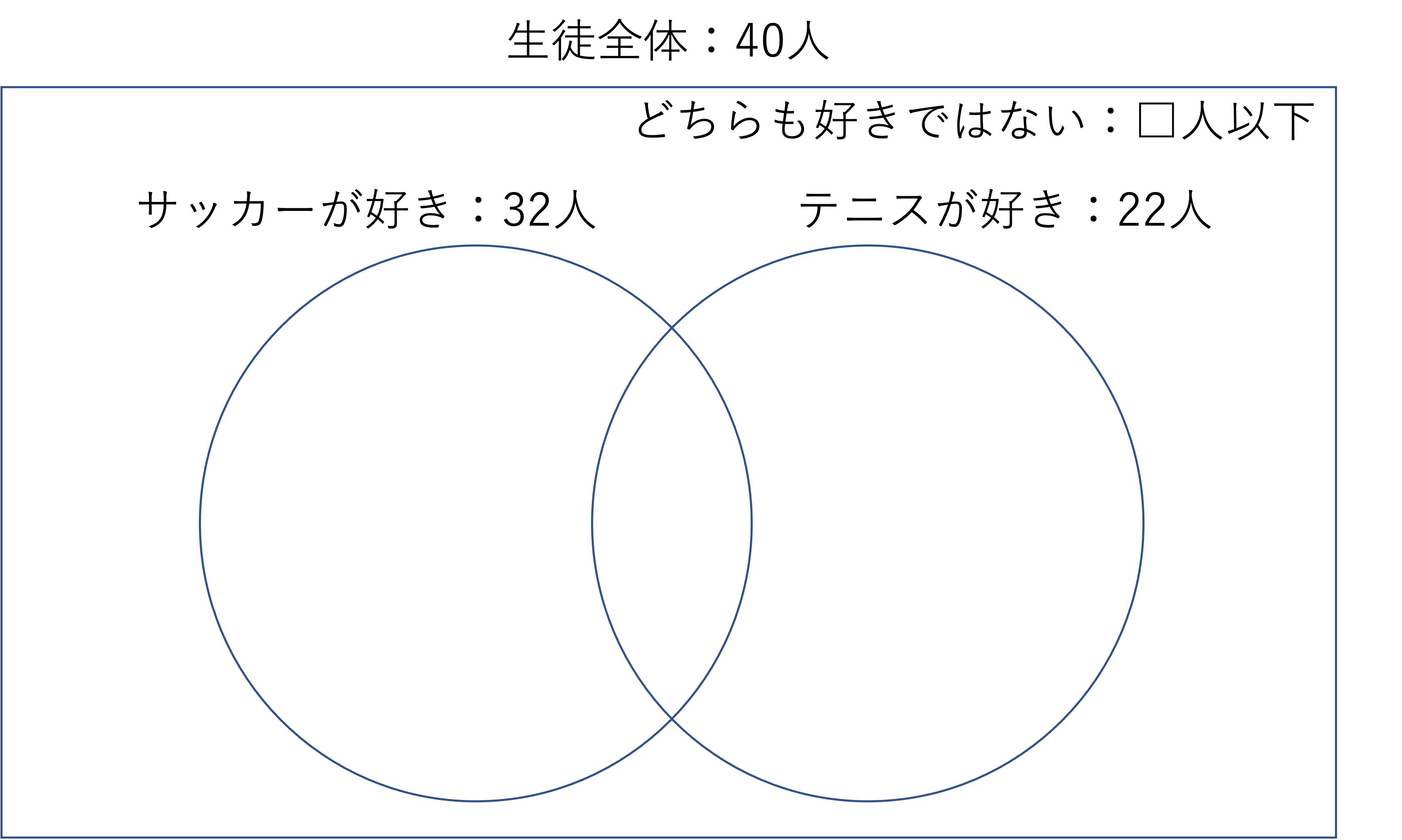
ここまで描き終わったら今回聞かれているものに注目します。今回出すべき答えはどちらも好きでない人が何人以下か,ということでした。ここで①で見出した解き方と同じ考え方をとってみましょう。○人以下というのは最大で○人というのと同じ意味を指します。そしてこのどちらも好きではない人が最大の人数であるとき,サッカーまたはテニス,もしくはその両方が好きな人の数は最小になります。
いまサッカーまたはテニス,もしくはその両方が好きな人=2つの円の内側に当てはまる人たちが最小のとき,片方の円の中にもう片方がすっぽり収まる形になります。今回で言うと,「サッカーが好き」が「テニスが好き」の中に入るか,「テニスが好き」が「サッカーが好き」の中に入るかの2択です。
しかし人数に注目すると,サッカーが好きな人の方が多いですよね。集合が重なるときは大きいものが小さいものを含むようになりますので,今回は「サッカーが好き」が外側に来ます。このときサッカーまたはテニス,もしくはその両方が好きな人の数は32人です。

そして先ほど説明したように,このときどちらも好きではない人の数が最大になります。そのときの人数は40-32=8人になりますので,生徒のうちサッカーもテニスも好きではない人の数は最大で8人,つまりは8人以下ということになります。
A.8人以下
この2問のように以下・以上を最大・最小と読み換えて解くテクニックは身に付けておくと集合山以外の問題でも活きてくることが多いです。ぜひ覚えてみてください。
問題③ 値が「人」じゃない集合算!
次はもう少し特殊な,値が人じゃない問題を解いてみましょう。値が人ではないというのは,グループに当てはまる人の数が示されるわけではないということを意味しますが,おそらく問題を見てもらったほうが早いでしょう。早速解いてみてください。
次の□にあてはまる数を答えなさい。
200人の中学生のうち,犬を飼っている人が全体の44%,ねこを飼っている人が全体の23%,犬とねこの両方を買っている人が全体の11%であるとき,犬とねこのどちらも飼っていない人は□人です。
(三田国際学園中学校(2018),一部改題)
解説③
それでは解説に移ります。いきなり数値が割合に変わって解きづらさを感じた人も多いかもしれませんが,それでもベン図に書く情報や考え方・解き方はこれまでの集合算と同じです。まずは文章中で挙げられている情報を整理するところから始めてみましょう。
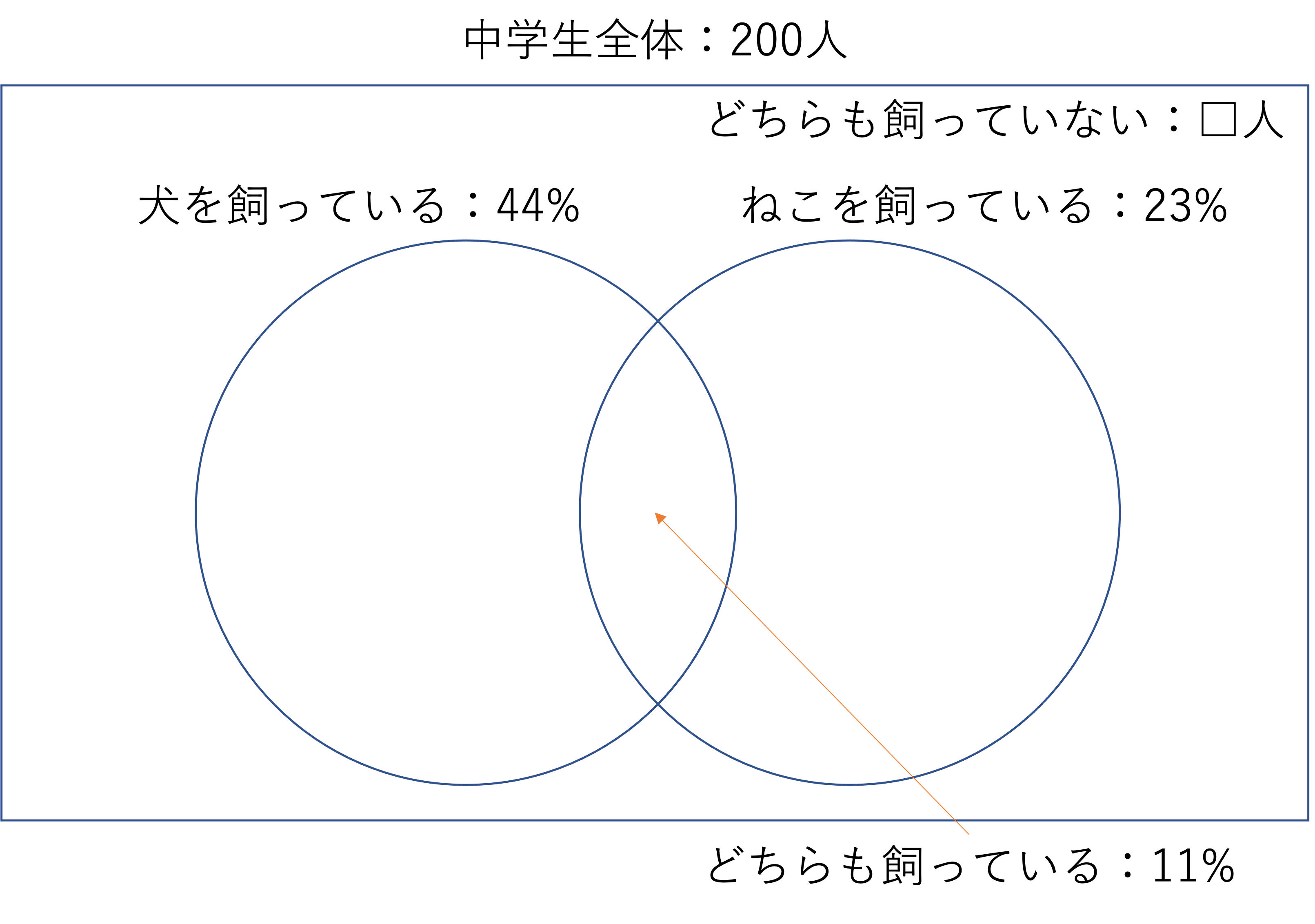
ここまで整理できたら後は①・②で解いた集合算と同じように進めていきましょう。今回求めるべき「どちらも飼っていない人」は,2つの円の外側に位置します。この部分の人の人数は,全体の200人に割合をかければ求められそうです。したがってまずは,2つの円の外側の人数の割合を考えていきましょう。
ここで2つの円の外側の割合は,全体から2つの円の内側に属する人の割合を引くことで求められます。2つの円の内側,つまり犬またはねこ,もしくはその両方を飼っている人の割合は,左側の欠けた円の部分+真ん中の重なった部分+右側の欠けた円の部分で求められます。いま真ん中の「両方飼っている人」の割合が11%であることから,左側の欠けた部分の割合は44-11=33%,右側の欠けた部分の割合は23-11=12%だと計算できるので,2つの円の内側は全体の56%を表すことが分かります。
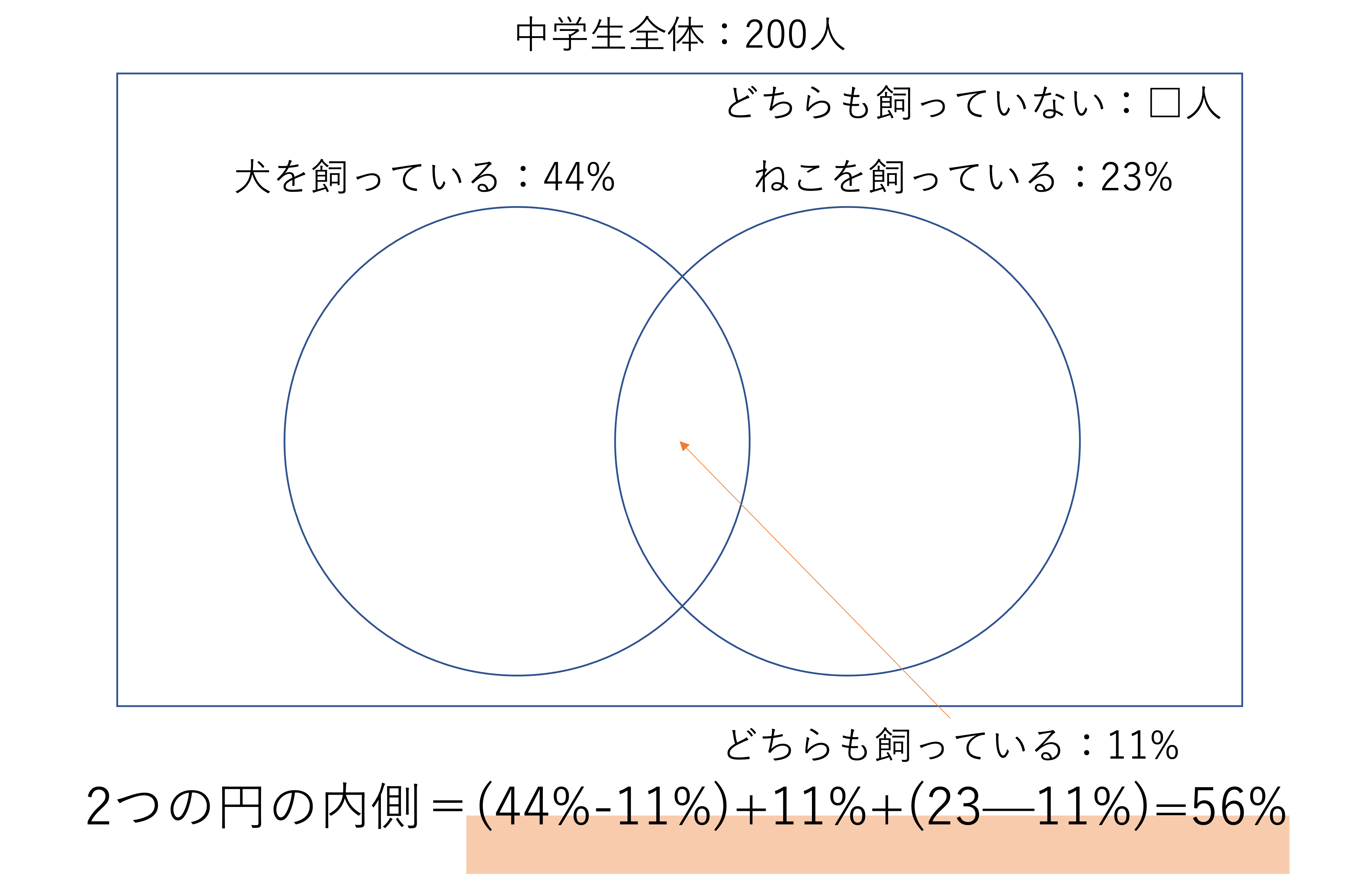
このことから,どちらも飼っていない人,すなわち2つの円の外側に該当する人の割合は100%-56%=44%になります。そして今回はどちらも飼っていない人の数を答えればいいので,正解は200×44÷100=88人となります。
A.88人
こんな風に,問題文と描いた図形を照らし合わせて考えていくと集合算は解きやすかったりします。円の内/外という説明がわかりづらかったかもしれませんが,そのような場合は手を動かしながら計算していくといいでしょう。
問題④ 分数の割合が登場する集合算!
続いても割合に関する集合算です。今回は分数が登場するのでやや手強いでしょう。計算ミスに気をつけて進めてみてください。
次のア,イにあてはまる数を答えなさい。
ある中学校では,運動部の生徒は全体の4/7,文化部の生徒は全体の1/3,運動部と文化部のどちらも入っていない生徒は全体の5/21,運動部と文化部の両方に入っている生徒は144人でした。この学校の全校生徒は(ア)人で,運動部のみに入っている生徒は(イ)人です。
(青山学院中等部(2020),一部改題)
解説④
ここからは4番目の問題の解説に移ります。そろそろベン図の描き方にも慣れてきた頃合いかと思われます。焦らずに情報を整理しながら進めていきましょう。
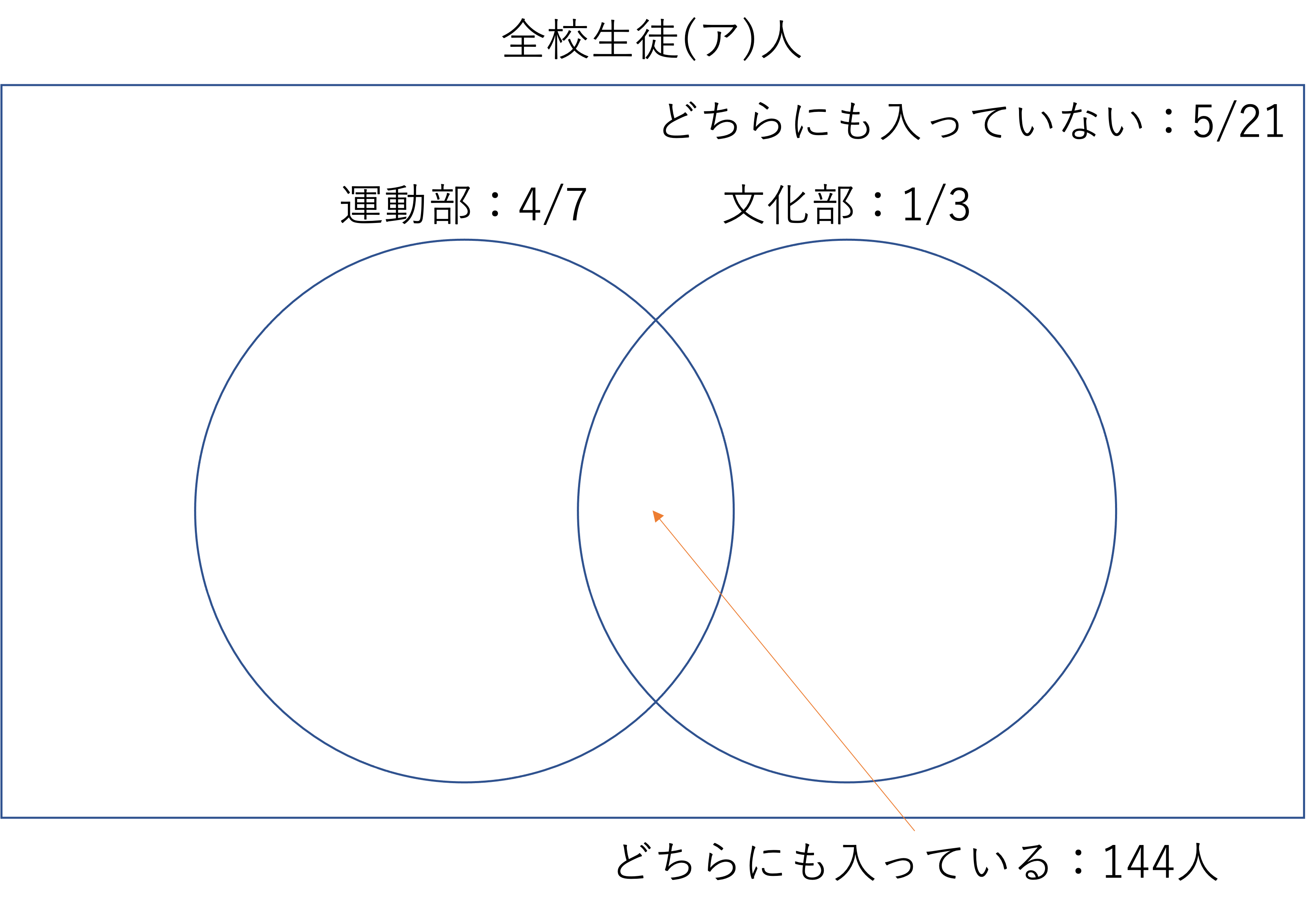
今回求めるべき数字は,全校生徒が何人かということと運動部のみに入っている人は何人かということです。全校生徒は四角の中全体を,運動部のみに入っている生徒は右の円のうち欠けた部分を指すので,そこに当てはまる人の数や割合を考えていきましょう。
まずは全体からです。いま,運動部にも文化部にも入っていない生徒の割合が全体の5/21だと問題文で提示されています。そのため運動部または文化部,もしくはその両方に入っている生徒の割合は1-5/21=16/21だということが分かります。
ここで,運動部または文化部,もしくはその両方に入っている生徒を別の方法で表してみましょう。このような生徒は2つの円の内側に該当します。上の問題で見たように,この2つの円の内側の割合や人数は,
左の欠けた円の部分+中央の重なった部分+右の欠けた円の部分
で計算することができます。いま真ん中の部分の割合がわからないので□で表すと,2つの円の内側に当てはまる生徒の割合は,(4/7-□)+□+(1/3-□)=19/21-□となります。ここでこれまで計算したことから,16/21=19/21-□という式が成立します。これを解くと□=3/21となるので,運動部にも文化部にも入っている人の割合は全体の3/21ということがわかります。いま,両方に入っている人の数は144人だったので,(ア)×3/21=144という式が成り立ちます。これを分数のかけ算に注意して計算していくと,(ア)=1008になりますので,全校生徒の人数は1008人になります。
続いて運動部だけに所属している人の数を考えていきましょう。前述したように,運動部のみに入っている人は左の欠けた円に該当します。そのため「文化部に入っている・いないにかかわらず運動部に入っている人」の数から「運動部にも文化部にも入っている人」の数を引くことで,(イ)の値を求めていきましょう。
いま全校生徒が1008人,運動部に入っている人の割合が4/7であることから,その人数は1008×4/7=576人だと分かります。そして問題文の中で登場した,両方に入っている人の数が144人だということを用いると,(イ)の数は576-144=432人だと計算できます。
A.(ア)1008人,(イ)432人
このようにある部分の大きさや割合を2通りで表して考えていくというのは中学受験で頻出するパターンの一つだと言えます。集合算に限らず頭に入れておくといいでしょう。
練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>
まとめ
今回は集合算に関する記事の応用編として,実際に入試で登場した問題を5つご紹介し,それを解説しながら集合算への理解を深めていくというものでした。5つの問題は全てベン図で解説してしまいましたが,表を使ったやり方でも計算できるでしょう。問題の答えそのものはどのやり方でも変わらないので,チャレンジしてみてもいいかもしれませんね。本記事が今後の学習の手助けとなれば幸いです。