皆さんは「てこと力のつり合い」の問題と聞いてどのようなことを思い浮かべますか? 「支点・力点・作用点は覚えてるけど、計算問題は難しそう……」「複雑な問題が多くて何から勉強を始めればいいかわからない……」という人が多いのではないでしょうか。実際、「てこと力のつり合い」は複雑な問題が簡単に作れてしまうので、さまざまな種類の問題があります。それぞれに解きやすい解法があり、そのすべてをいっぺんに覚えようとするのは大変ですし、混乱のもととなります。今回は、 棒 を使って説明していきます。
だからこそ、てこと力のつり合いの問題に関してわからないところを一つひとつ解決し、混乱がおきないようにしましょう。てこと力のつり合いについて基礎的な問題は以下の記事で解説しているので、「てこについて全く分からない!」という人はぜひ参考にしてみてください。

今回はそんな「てこと力のつり合い」の中でも苦手意識を持っている人が多いであろう「太さが一様でない棒」が使われる問題を中心に解説していきます。例えば、次のような問題です。
問題
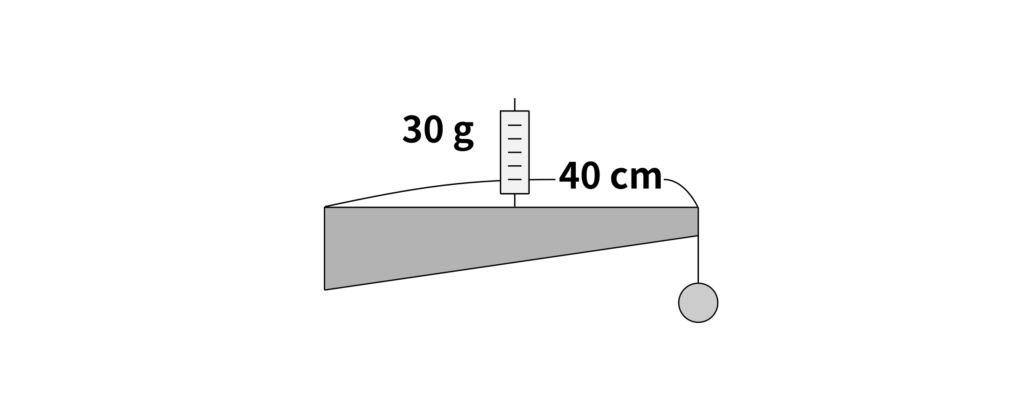
長さが\(40\,\mathrm{cm}\)で、重さが\(20\,\mathrm{g}\)の太さが一様でない棒がある。この棒の右端に、以下のようにおもりをつるし、中心をばねばかりで支えた。ばねばかりが示す値は\(30\,\mathrm{g}\)であった。棒は水平になっている。このとき、以下の問題に答えなさい。
(1) 棒の右端につるしたおもりの重さは何\(\,\mathrm{g}\)でしょうか。
(2) 棒の重心は、棒の左端から何\(\,\mathrm{cm}\)のところにあるでしょうか。
この記事では以下のことを説明します。
- 力のつり合いには「上下の力のつり合い」と「モーメントのつり合い」の二つがある
- モーメントの大きさは、「支点」の位置を決めた上で、(モーメントの大きさ)=(支点からの距離)×(重さ)で求める
- 棒の太さが一様ではない場合、力のつり合いから重心の位置を求める
- 棒の太さが一様でない場合は、重さを無視できる一様な棒に、もとの棒の重さと同じおもりを棒の重心につるした場合と同じ
では解説に入ります。
Contents
まずは 棒 の重さが一様のときの問題を解いてみよう!
まずは、棒の重さが一様である場合の注意点を復習しましょう。次の問題の答えを考えてみてください。
問題
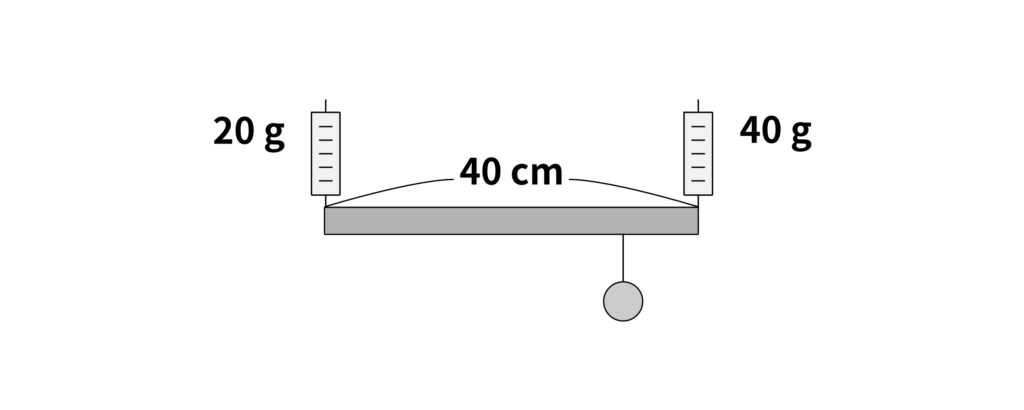
長さが\(40\,\mathrm{cm}\)で、重さが\(20\,\mathrm{g}\)の太さが一様な棒がある。この棒に、以下のようにおもりをつるし、両端をばねばかりで支えた。ばねばかりが示す値はそれぞれ\(20\,\mathrm{g}\)、\(40\,\mathrm{g}\)であった。棒は水平になっている。このとき、以下の問題に答えなさい。
(1) 棒につるしたおもりの重さは何\(\,\mathrm{g}\)でしょうか。
(2) おもりは棒の左端から何\(\,\mathrm{cm}\)の場所につるされているでしょうか。
解答
力のつり合いには「上下の力のつり合い」と「モーメントのつり合い」の二つがあります。「モーメントのつり合い」は「回転する力のつり合い」とよばれることもあります。モーメントの大きさは、「支点」の位置を決めた上で、
(モーメントの大きさ)=(支点からの距離)×(重さ)
で求めることができます。「上下の力のつり合い」と「モーメントのつり合い」という二つが成立してはじめて、物体は静止するのです。はじめに「支点」の位置を決めることが必要です。このことを念頭に問題を解いてみましょう。
(1) まずは、「上下の力のつり合い」を考えます。ばねばかりにかかっている力は合計で
\(20\,\mathrm{g} + 40\,\mathrm{g} = 60\,\mathrm{g}\)
です。これが「上向きの力」になります。次に、棒の重さとおもりの重さの合計を考えます。おもりの重さを仮に□\(\,\mathrm{g}\)とすると、
\(20\,\mathrm{g} + \text{□}\,\mathrm{g}\)
です。これが「下向きの力」になります。最後に、「上下の力のつり合い」を考えると、
\(60\,\mathrm{g} = 20\,\mathrm{g} + \text{□}\,\mathrm{g}\)
となります。したがって、おもりの重さは
\(60\,\mathrm{g} – 20\,\mathrm{g} = 40\,\mathrm{g}\)
と求めることができます。
(2) 次に、「モーメントのつり合い」を考えます。棒の左端を支点と考え、おもりの左端からの距離を\(\text{□}\,\mathrm{cm}\)とすると、棒とおもりによるモーメントは
\(20\,\mathrm{g} \times 20\,\mathrm{cm} + 40\,\mathrm{g} \times \text{□}\,\mathrm{cm}\)
となります。これが「支点を中心に時計回りに回転する力」です。ここで、太さが一様な棒の重さは、重さを無視していい棒の中心に、もとの棒の重さのおもりをつり下げるのと同じです。なので、左端から\(50\,\mathrm{cm} \div 2 = 25\,\mathrm{cm}\)の位置に\(20\,\mathrm{g}\)のおもりをつり下げたと想定してモーメントを考えています。
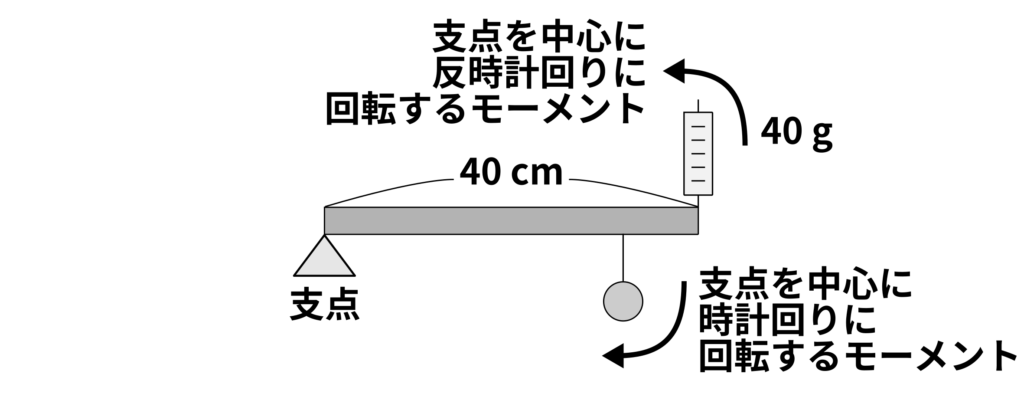
次に、右端のばねばかりによるモーメントは
\(40\,\mathrm{g} \times 40\,\mathrm{cm}\)
となります。これが「支点を中心に反時計回りに回転する力」です。
最後に、「モーメントのつり合い」を考えると、
\(20\,\mathrm{g} \times 20\,\mathrm{cm} + 40\,\mathrm{g} \times \text{□}\,\mathrm{cm} = 40\,\mathrm{g} \times 40\,\mathrm{cm}\)
となります。したがって、おもりの左端からの距離は
\(40\,\mathrm{cm}\)
と求めることができます。「上下の力のつり合い」と「モーメントのつり合い」の両方を考えるということや、太さが一様で重さのある棒は、同じ重さのおもりを中心につりさげたのと同じということを思い出すことができたでしょうか?
棒 の重さが一様でないときはどうするの? 棒の重心がどこかを考えてみよう
次は、棒の太さが一様でない場合の問題について考えます。棒の太さが一様なときと一様でないときで、どのような違いがあるでしょうか?
その違いは「棒の重心の位置」です。棒の太さが一様な場合は、重さを無視できる棒に、もとの棒の重さと同じおもりを棒の中心につるした場合と同じだということを先程の問題で確認しましたね。一方、棒の太さが一様でない場合は、もとの棒の重さと同じおもりを用意するのは同じですが、そのつるす位置が必ずしも中心ではなくなります。物によっては極端に右、あるいは左にかたよっているかもしれません。

棒の太さが一様ではない場合、重心の位置を求めてから問題を解くことが重要になります。では、この重心の位置をどのようにして調べたらよいのでしょうか? それは先ほども解説した「上下の力のつり合い」と「モーメントのつり合い」によってわかります! つまり棒の太さが一様でない場合でも、この二つのつり合いをもとに問題を解けばよいことになります。
原理は理解できたでしょうか? では、次の問題を解いてみましょう。
問題
長さが\(40\,\mathrm{cm}\)で、重さが\(20\,\mathrm{g}\)の太さが一様でない棒がある。この棒の右端に、以下のようにおもりをつるし、中心をばねばかりで支えた。ばねばかりが示す値は\(30\,\mathrm{g}\)であった。棒は水平になっている。このとき、以下の問題に答えなさい。
(1) 棒の右端につるしたおもりの重さは何\(\,\mathrm{g}\)でしょうか。
(2) 棒の重心は、棒の左端から何\(\,\mathrm{cm}\)のところにあるでしょうか。

解答
前の問題と同じように、「上下の力のつり合い」と「モーメントのつり合い」をもとに問題を解いていきましょう。
(1) まずは、「上下の力のつり合い」を考えます。ばねばかりにかかっている力は問題文で与えられているように、\(30\,\mathrm{g}\)です。これが「上向きの力」になります。次に、棒の重さとおもりの重さの合計を考えます。おもりの重さを仮に\(\text{□}\,\mathrm{g}\)とすると、
\(20\,\mathrm{g} + \text{□}\,\mathrm{g}\)
です。これが「下向きの力」になります。最後に、「上下の力のつり合い」を考えると、
\(30\,\mathrm{g} = 20\,\mathrm{g} + \text{□}\,\mathrm{g}\)
となります。したがって、おもりの重さは
\(30\,\mathrm{g} – 20\,\mathrm{g} = 10\,\mathrm{g}\)
と求めることができます。
(2) 次に、「モーメントのつり合い」を考えます。棒の左端を支点と考え、棒の重心の左端からの距離を\(\text{□}\,\mathrm{cm}\)とすると、棒とおもりによるモーメントは
\(20\,\mathrm{g} \times \text{□}\,\mathrm{cm} + 10\,\mathrm{g} \times 40\,\mathrm{cm}\)
となります。これが「支点を中心に時計回りに回転する力」です。ここで、太さが一様な棒の重さは、重さを無視していい棒の中心に、もとの棒の重さのおもりをつり下げるのと同じです。なので、左端から\(50\,\mathrm{cm} \div 2 = 25\,\mathrm{cm}\)の位置に\(20\,\mathrm{g}\)のおもりをつり下げたと想定してモーメントを考えています。
次に、ばねばかりによるモーメントは
\(30\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。これが「支点を中心に反時計回りに回転する力」です。最後に、「モーメントのつり合い」を考えると、
\(20\,\mathrm{g} \times \text{□}\,\mathrm{cm} + 10\,\mathrm{g} \times 40\,\mathrm{cm} = 30\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。したがって、おもりの左端からの距離は
\(10\,\mathrm{cm}\)
と求めることができます。おもりの重さが一様でないときも、「上下の力のつり合い」と「モーメントのつり合い」という二種類のつり合いを考えればよいことがわかったでしょうか? 棒の太さが一様な場合と一様でない場合の本質的な違いは「重心の位置」だけなので、解法に大きな違いがあるというわけでもありません。難しく考えずに、棒の重心の位置がどこなのかに焦点をあてて考えてみましょう!
太さが一様でない 棒 を使った入試問題に挑戦!
では、ここまでで学習した知識を使って入試問題に挑戦してみましょう。
問題
長さが\(40\,\mathrm{cm}\)で重さが\(50\,\mathrm{g}\)の棒Aと長さが\(60\,\mathrm{cm}\)で重さが\(50\,\mathrm{g}\)の棒Bがある。図1のように、棒の両端を糸で支えると、棒Aの左の糸には\(20\,\mathrm{g}\)、右の糸には\(30\,\mathrm{g}\)の重さがかかり、棒Bの左の糸には\(10\,\mathrm{g}\)、右の糸には\(40\,\mathrm{g}\)の重さがかかった。(愛光中学校2019年 一部改題)

(1) 棒A、Bをそれぞれ1本の糸で支えて水平にするには、棒の左端から何\(\,\mathrm{cm}\)のところを支えればよいか。
解答 (1)
「1本の糸で支えて水平にする」には、棒の重心を糸で支える必要があります。なので、それぞれの棒の重心を求めましょう。
棒Aの左の糸には\(20\,\mathrm{g}\)、右の糸には\(30\,\mathrm{g}\)の重さがかかっています。今、棒Aの重心が左端から\(\text{□}\,\mathrm{cm}\)のところにあるとします。この重心を支点としたとき、左の糸によるモーメントは
\(20\,\mathrm{g} \times \text{□}\,\mathrm{cm}\)
となります。これが「支点を中心に時計回りに回転する力」です。次に、右の糸によるモーメントは
\(30\,\mathrm{g} \times 40 – \text{□}\,\mathrm{cm}\)
となります。これが、「支点を中心に反時計回りに回転する力」です。最後に、「モーメントのつり合い」を考えると、
\(20\,\mathrm{g} \times \text{□}\,\mathrm{cm}\) = \(30\,\mathrm{g} \times (40 – \text{□}\,\mathrm{cm}) \)
となります。したがって、棒Aの重心の左端からの距離は
\(24 \,\mathrm{cm}\)
と求めることができます。
棒Bに対してもおなじように、棒Bの重心を左から\(\text{□}\,\mathrm{cm}\)としたうえで、左の糸によるモーメントと右の糸によるモーメントのつり合いを考えると、
\(10\,\mathrm{g} \times \text{□}\,\mathrm{cm}\) = \(40\,\mathrm{g} \times (60 – \text{□}\,\mathrm{cm}) \)
となります。したがって、棒Bの重心の左端からの距離は
\(48\,\mathrm{cm}\)と求めることができます。
(2) 図2のように、棒Aの真ん中と右端を糸で支えて水平にすると、右の糸が支える重さは何\(\,\mathrm{g}\)になるか。

解答 (2)
支点を棒の中心として「モーメントのつり合い」を考えましょう。
棒Aの中心は左端から\(24\,\mathrm{cm}\)のところにあるので、左端から\(20\,\mathrm{cm}\)のところにある棒の中心からの距離は
\(24\,\mathrm{cm} – 20\,\mathrm{cm} = 4\,\mathrm{cm}\)
となります。これより、棒Aによるモーメントは
\(50\,\mathrm{g} \times 4\,\mathrm{cm}\)
となります。次に、右端の糸が支える重さを\(\text{□}\,\mathrm{g}\)とすると、右の糸による力のモーメントは
\(\text{□}\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。最後に、「モーメントのつり合い」を考えると、
\(50\,\mathrm{g} \times 4\,\mathrm{cm} = \text{□}\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。したがって、右端の糸が支える重さは
\(10\,\mathrm{g}\)
と求めることができます。
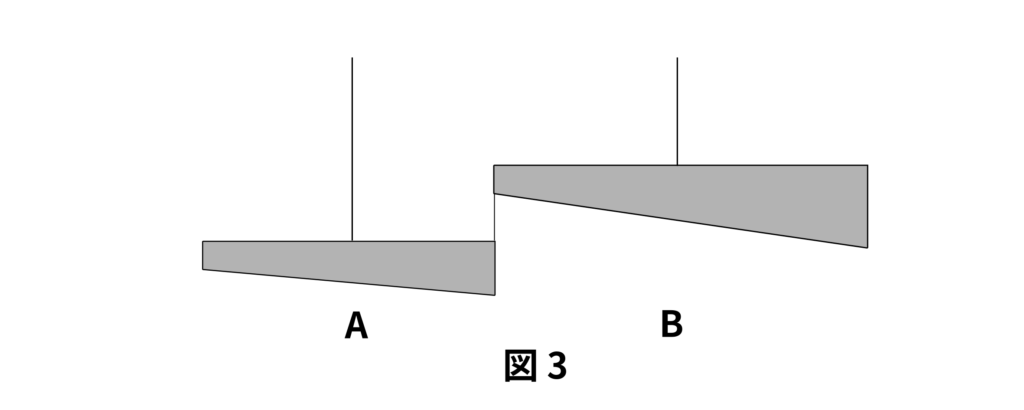
次に、図3のように、棒A、Bの真ん中をそれぞれ糸で支えながら、棒Aの右端と棒Bの左端を糸で繋ぐ。このままでは棒Bは右にかたむいてしまうので、次の2つの方法で水平にしたい。
(3) 棒Bに重さが\(30\,\mathrm{g}\)のおもりをつるすとき、左端から何\(\,\mathrm{cm}\)のところにつるせばよいか。
(4) 棒Bを支えている糸をずらすとき、糸を左端から何\(\,\mathrm{cm}\)の位置にずらせばよいか。
解答 (3)
一見複雑に見えますが、問題(2)の結果を使えば簡単な形になります。問題(2)を思い出してみると、棒Aの中心と右端をそれぞれ糸で支えており、棒Aは水平になっています。一方で今の問題を見てみると、棒Aの中心と右端がそれぞれ糸で支えられており、棒Aと棒Bを水平にすることが目標です。つまり、「棒Aを水平にする」という目標は問題(2)の状況で達成されています。なので、棒Aに関しては問題(2)の状況をそのまま当てはめれば大丈夫です。これより、棒Aの右端の糸にかかる重さは問題(2)の答えより、
\(10\,\mathrm{g}\)
となります。よって、棒Bは左端に\(10\,\mathrm{g}\)のおもりがつるされた状況と同じになります。この状況で、さらに\(30\,\mathrm{g}\)のおもりをつるすことで、「モーメントのつり合い」を実現し、棒を水平にします。支点を棒Bの中心とすると、棒Bの重心は左端から\(48\,\mathrm{cm}\)のところにあるので、左端から\(30\,\mathrm{cm}\)のところにある棒の中心からの距離は
\(48\,\mathrm{cm} – 30\,\mathrm{cm} = 18\,\mathrm{cm]}\)
となります。これより、棒Bによるモーメントは
\(50\,\mathrm{g} \times 18\,\mathrm{cm}\)
となります。次に、棒Bの右端の糸によるモーメントは
\(10\,\mathrm{g} \times 30\,\mathrm{cm}\)
となります。また、おもりをつるす位置を左端から\(\text{□}\,\mathrm{cm}\)の位置とすると、このおもりによるモーメントは
\(30\,\mathrm{g} \times (30\,\mathrm{cm} – \text{□}\,\mathrm{cm}) \)
となります。最後に、「モーメントのつり合い」を考えると
\(50\,\mathrm{g} \times 18\,\mathrm{cm} = 10\,\mathrm{g} \times 30\,\mathrm{cm} + 30\,\mathrm{g} \times (30\,\mathrm{cm} – \text{□}\,\mathrm{cm}) \)
となります。したがって、棒Bにつるすおもりの左端からの距離は
\(10\,\mathrm{cm}\)
と求めることができます。
解答 (4)
この問題は(3)と同じように「モーメントのつり合い」から求めることができます。棒Aが水平になるためには棒Bの左端に\(10\,\mathrm{g}\)の力がかかります。支点を糸の位置として、この糸の位置を左端から\(\text{□}\,\mathrm{cm}\)の位置とすると、棒Bの重心の支点からの距離は
\(48\,\mathrm{cm} – \text{□}\,\mathrm{cm}\)
となります。これより、棒Bのモーメントは
\(50\,\mathrm{g} \times (48\,\mathrm{cm} – \text{□}\,\mathrm{cm}) \)
となります。次に棒Bの右端の糸によるモーメントは
\(10\,\mathrm{g} \times \text{□}\,\mathrm{cm}\)
となります。最後に、「モーメントのつり合い」を考えると
\(50\,\mathrm{g} \times (48\,\mathrm{cm} – \text{□}\,\mathrm{cm}) – 10\,\mathrm{g} \times \text{□}\,\mathrm{cm}\)
となります。したがって、棒Bを支える糸の左端からの距離は
\(40\,\mathrm{cm}\)
と求めることができます。
太さが一様でない棒についての便利なサイト→https://www.e-voyage.net/entry/spring18
まとめ……の前に


















