今回は集合算について取り扱って行きます。集合というのは高校で詳しく習う単元であるため,中学入試レベルで完璧に理解するのは難しいかと思われますが,どの中学校で出題されてもおかしくないのできっちり対策しておきたいところです。そこで今回は解き方を中心に集合算を解説していきたいと思います。
Contents
集合とは?
そもそも集合とは何を指すのでしょうか。集合とは簡単に言ってしまえば,あるモノをたくさん集めたグループのことです。この集合というのは,別に算数に限って使われる用語ではありません。学年やクラスやクラブ活動だって,同じ年齢で・同じ趣味で,という区分がなされた1つの集合です。
算数に絞って説明するならば,3桁の数とか偶数奇数といった数の集まりを集合と呼ぶことが可能です。学校の授業などで集合という単語そのものは登場しないかもしれませんが,このようなグループに基づいた問題を解いたり仲間分けをしたりする機会はこれまでたくさんあったのではないでしょうか。「集合」と言う単語にとらわれず,何かしらの特徴がある数字の集まりなのだ,ゆるく捉えていただけるといいでしょう。

集合算の例題を見てみよう!
それではここからは例題を取り上げながら,どんな問題が集合算なのか確認していきましょう。下のような問題が典型例になります。
30人のクラスで算数のテストをしました。問題は2問で,1問目が正解の人は14人,1問目が正解で2問目が不正解の人は8人,1問目も2問目も不正解の人は4人でした。
なんだかちゃんとした算数というよりは頭の体操みたいな問題ですよね。ここからは少し問題の分析を行い,その上で2つの解き方をご紹介します。
例題を分析してみると…
さて上で引用した例題を解く前に,この例題を使いながら集合算に出くわしたら確認するべきポイントをご紹介します。それは2つの軸の存在です。
上の問題に注目してみましょう。色々な情報が登場していますが,テストの1問目に解けたか解けなかったか・2問目に解けたか解けなかったか,という2つの区分がなされていることが分かりますね。そしてそれぞれの区分に応じて解けた/解けなかったという評価が与えられていることから,ここでは軸と読んでいます。もしかしたら難しい問題だと3つ・4つと軸が増えるかもしれませんが,基本的には集合算では2つの軸が提示されていることがほとんどです。問題に出会ったら,評価軸はどこかと目を凝らしてみるといいでしょう。
そしてより重要なことが,2つの軸によって4種類のグループが生まれているということです。今回であれば,
- 1問目も2問目も解けた人
- 1問目だけ解けた人
- 2問目だけ解けた人
- 1問目も2問目も解けなかった人
という4つにクラス全員が振り分けられますね。このような2つの軸の存在,そしてそこから生まれる4つのグループの存在が必ず集合算では示唆されています。その点に注意して解いていくといいでしょう。
解き方① 表を作ろう!
それでは集合算の大まかな構造を理解したところで,上で挙げた2つの軸または4つのグループをもとに問題を解いていく方法をご紹介します。その方法の1つ目は,表を作るというものです。表というのは2つの軸で構成されていますね。例えばカレンダーなども,第何週か+何曜日か,という2つの軸で作られています。そのため集合算の答えを出すのにぴったりだというわけです。集合算では下のような表を作るといいでしょう。このような表を作成すると,1問目・2問目という軸が存在すること,その軸によって4つのグループが作られることが一目瞭然です。
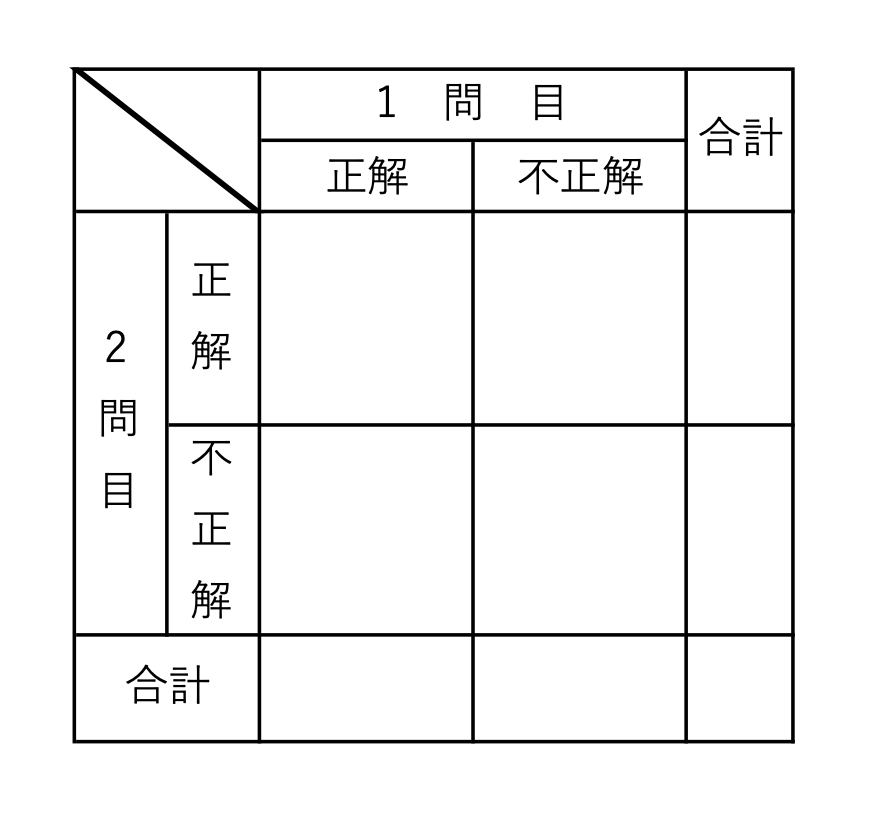
そしてこの表の中に数字を書き込むことで問題の答えを導いていきます。書き込むといってもどこから手をつければいいのかわからない人が多いかと思いますが,そこまで深く考えず,問題に出てくる数字を順番に適切なところに入力していくだけで大丈夫です。
例えば今回は初めに,30人のクラスということばが登場していました。このことは1問目を解いた人の合計が,また2問目を解いた人の合計が30人であることを意味しますので,次のように埋めることができます。
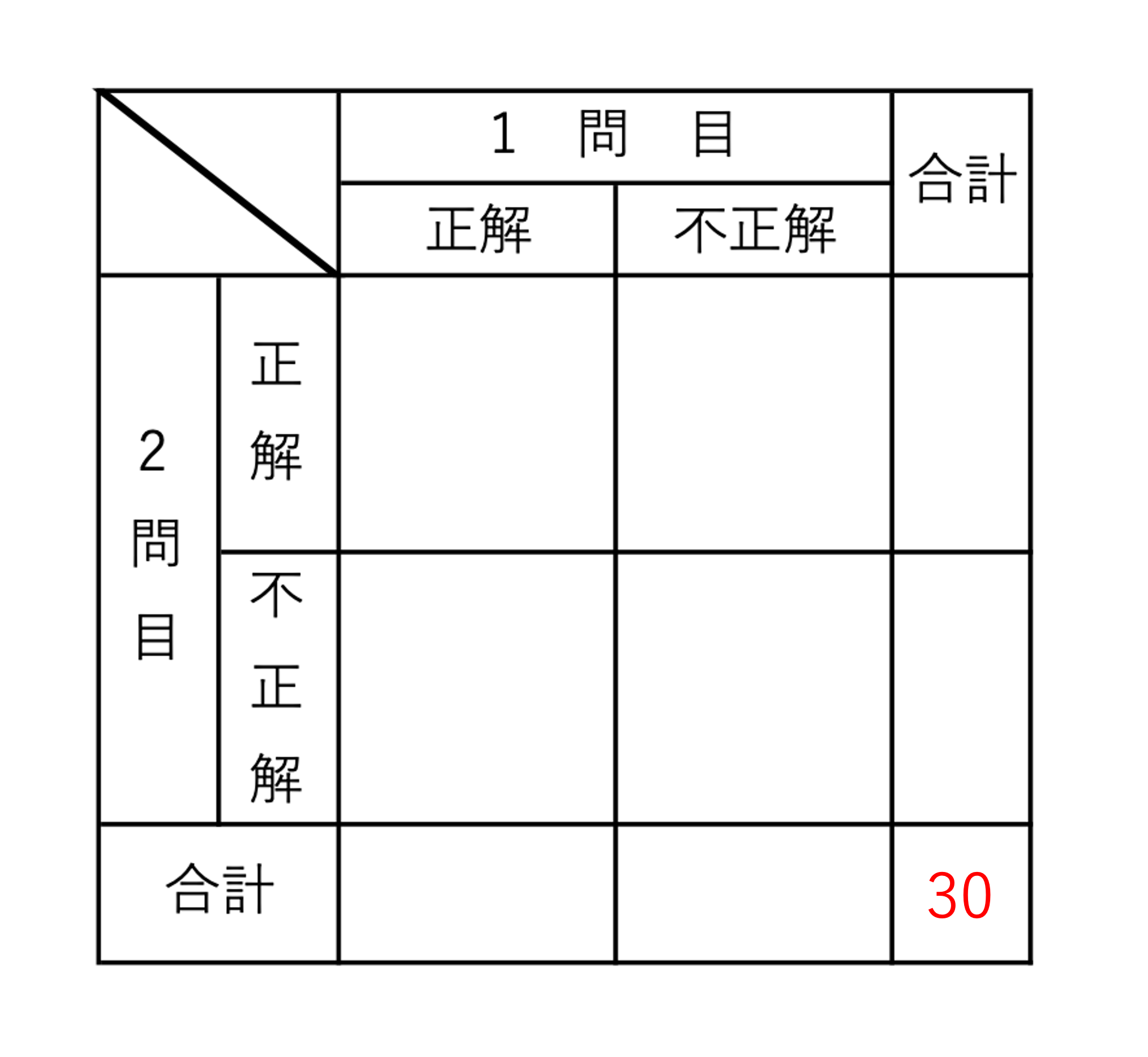
どんどんいきましょう。次に登場する言葉は,1問目が正解の人は14人というものです。ここで注意したいことが,1問目が解けただけであって2問目が解けたかどうかは分からない,ということです。そのため2問目の結果にかかわらず1問目を解けた人の合計という意味で次のように14という数字を書きます。集合算を解く上で,どこに書くかという部分には注意していきたいところです。
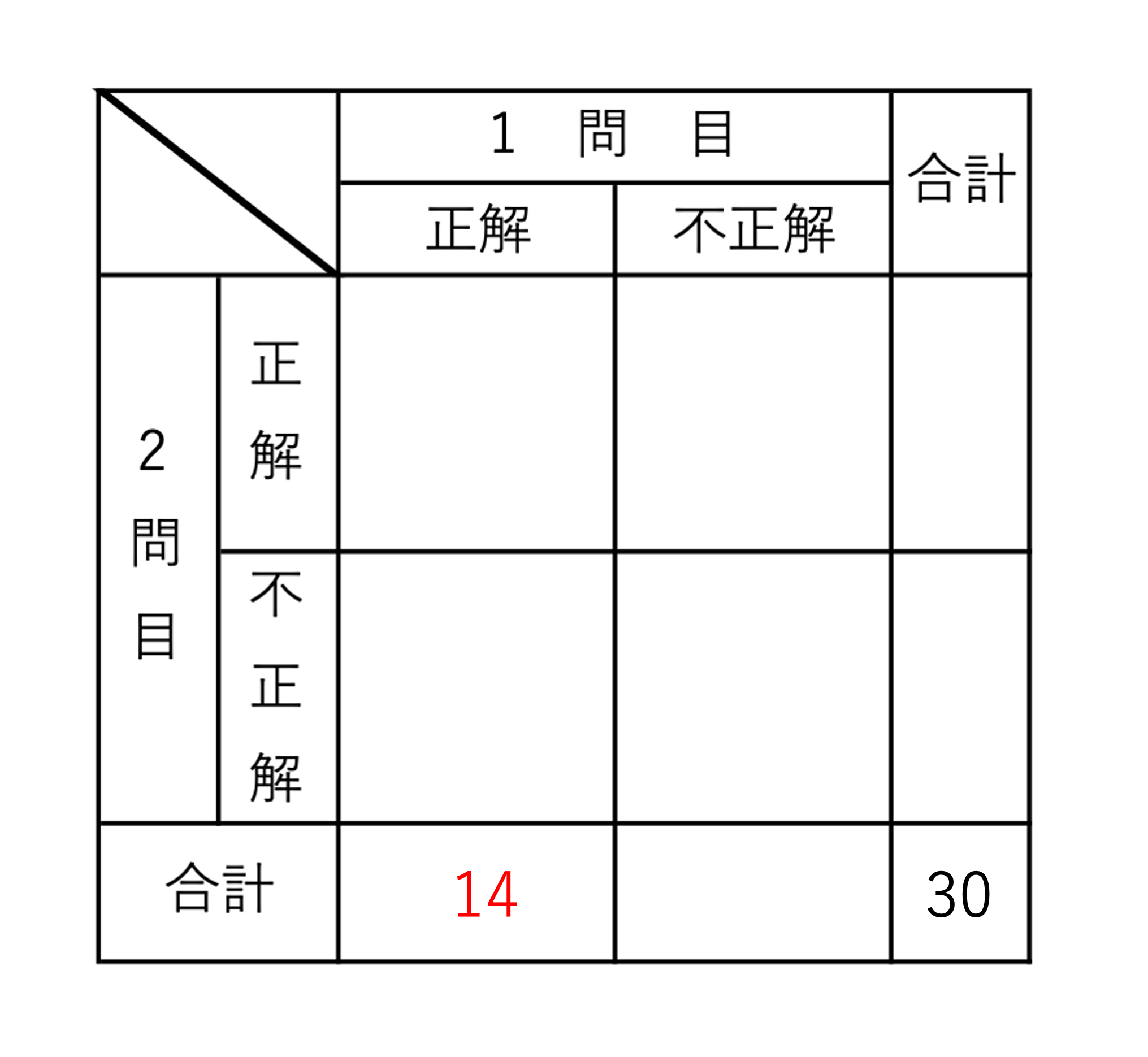
同じようにして,1問目が正解で2問目が不正解の人は8人・1問目も2問目も不正解の人は4人という数字も書き込んでいきます。こちらは先程の14人の箇所より,どこに記入すればいいかが分かりやすいですね。
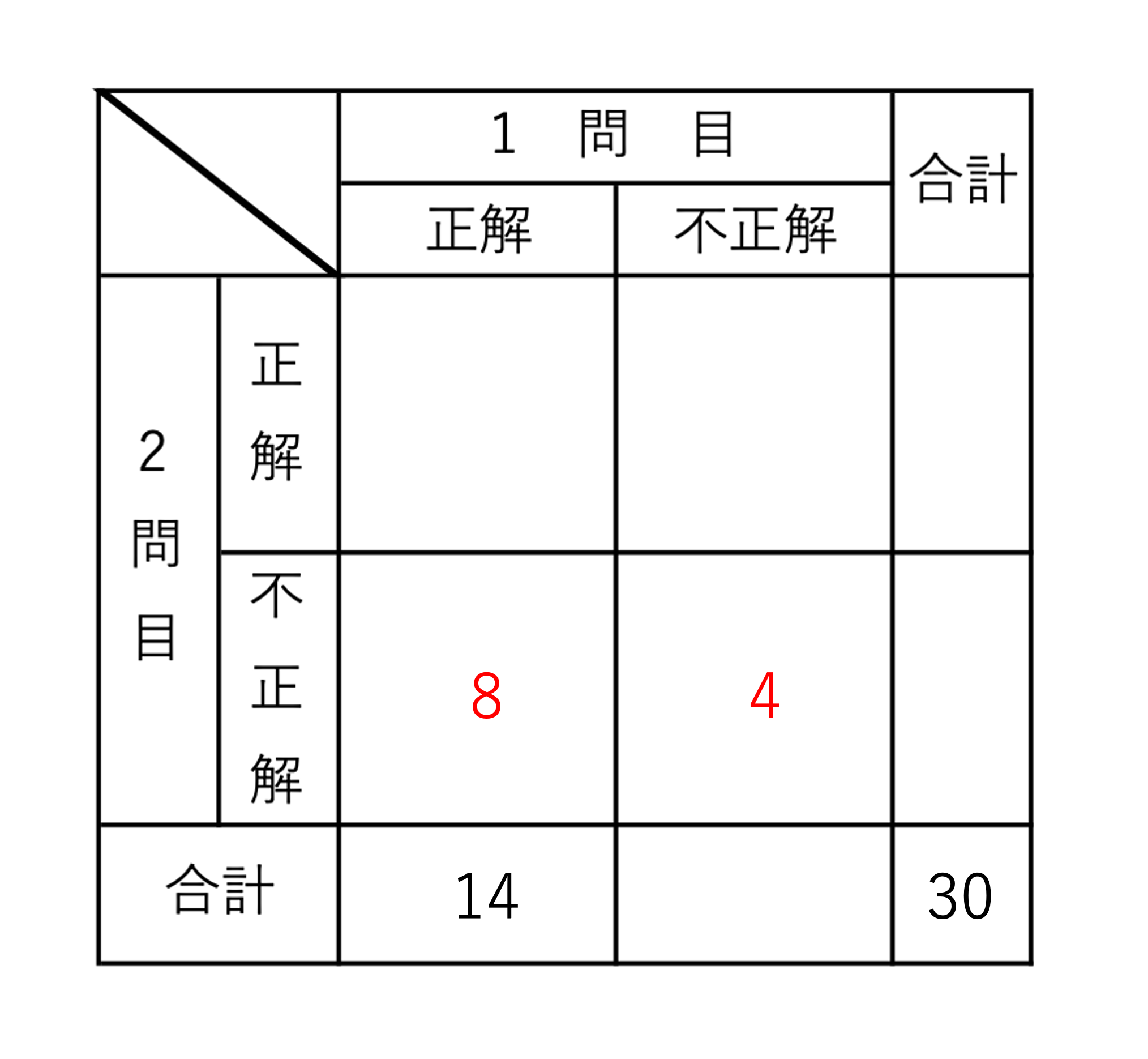
これにて問題文で登場した数値を埋め込む作業は完了です。あとはここからそれぞれの数値を導き出すことが集合算のよくあるパターンになります。そのためこの章では表を埋め切るところまで進めてしまいましょう。上の表で空欄は5箇所ありますが,まずは1問目が不正解だった人の欄に数字を書き込めそうですね。クラスの全ての人は1問目が解けたか解けなかったかのいずれかになり,解けた人が14人ということは解けなかった人は30-14=16人いるということです。
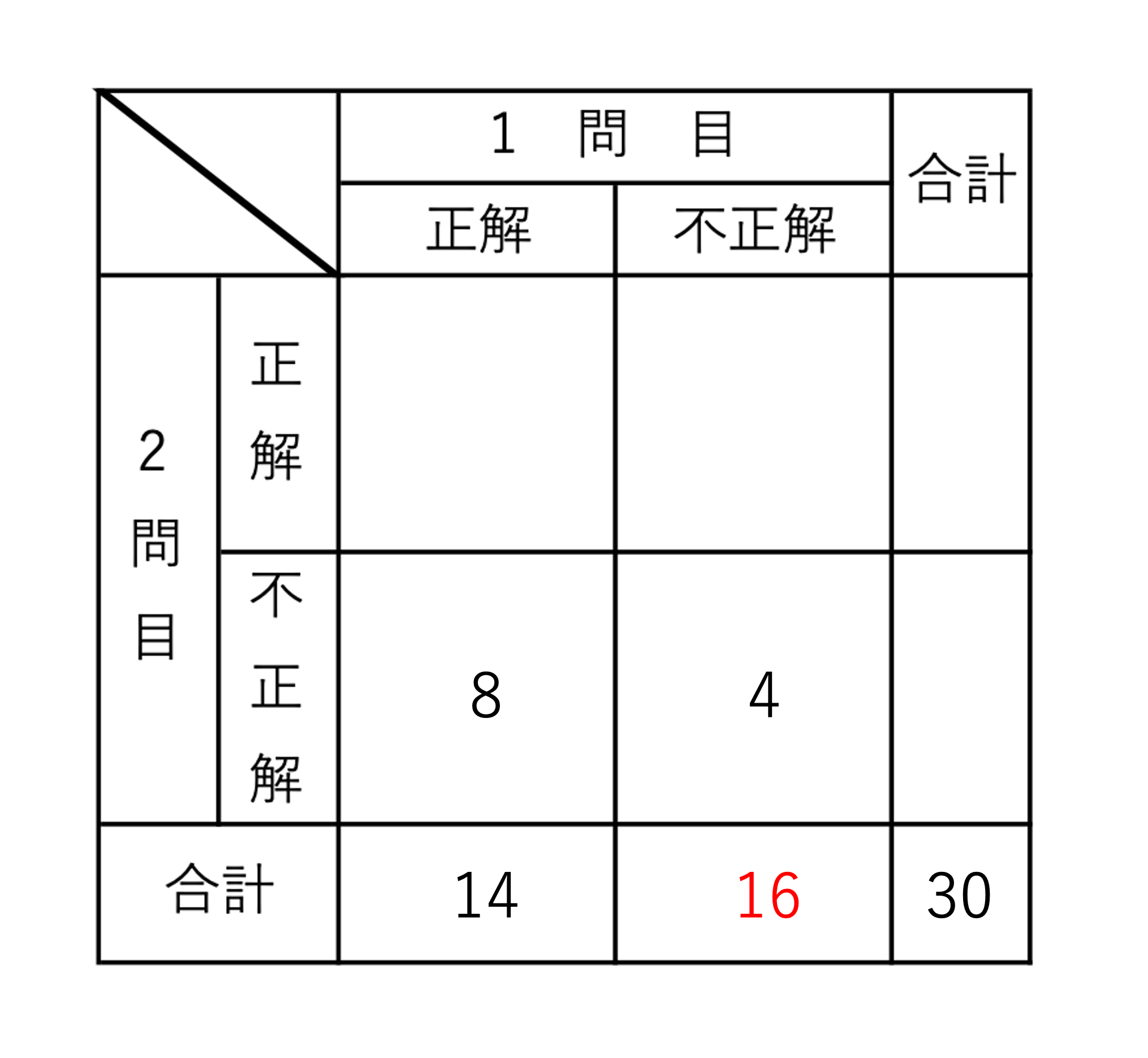
このように考えていくとなんだかパズルみたいですよね。このように問題文の解読さえしてしまえば,残りは遊び感覚で溶けるのが集合算の特徴です。ということで,残りの数字は一気に埋めてしまいましょう。どの順番で考えてもいいのですが,2問目の不正解者の合計をまずは見ていきましょう。2問目が不正解だった人には,1問目で正解だった人と不正解だった人が存在します。いま前者が8人,後者が4人だったことから,不正解者の合計は8+4=12人だとわかります。
このようにしていくと,2問目の正解者の合計も導き出せますね。クラス全体が30人,うち12人が2問目で不正解ということは,2問目の正解者は30-12=18人です。続いて1問目・2問目のどちらともに正解した人に注目します。1問目で正解した人は14人で,うち8人が2問目では不正解だったということなので,両方に正解したのは14-8=6人になります。最後に1問目に不正解・2問目に正解の人を埋めましょう。いま1問目に不正解だった人の合計は16人でした。このうち4人が2問目でも不正解だったということなので,当てはまる数字は16-4=12人だとわかります。
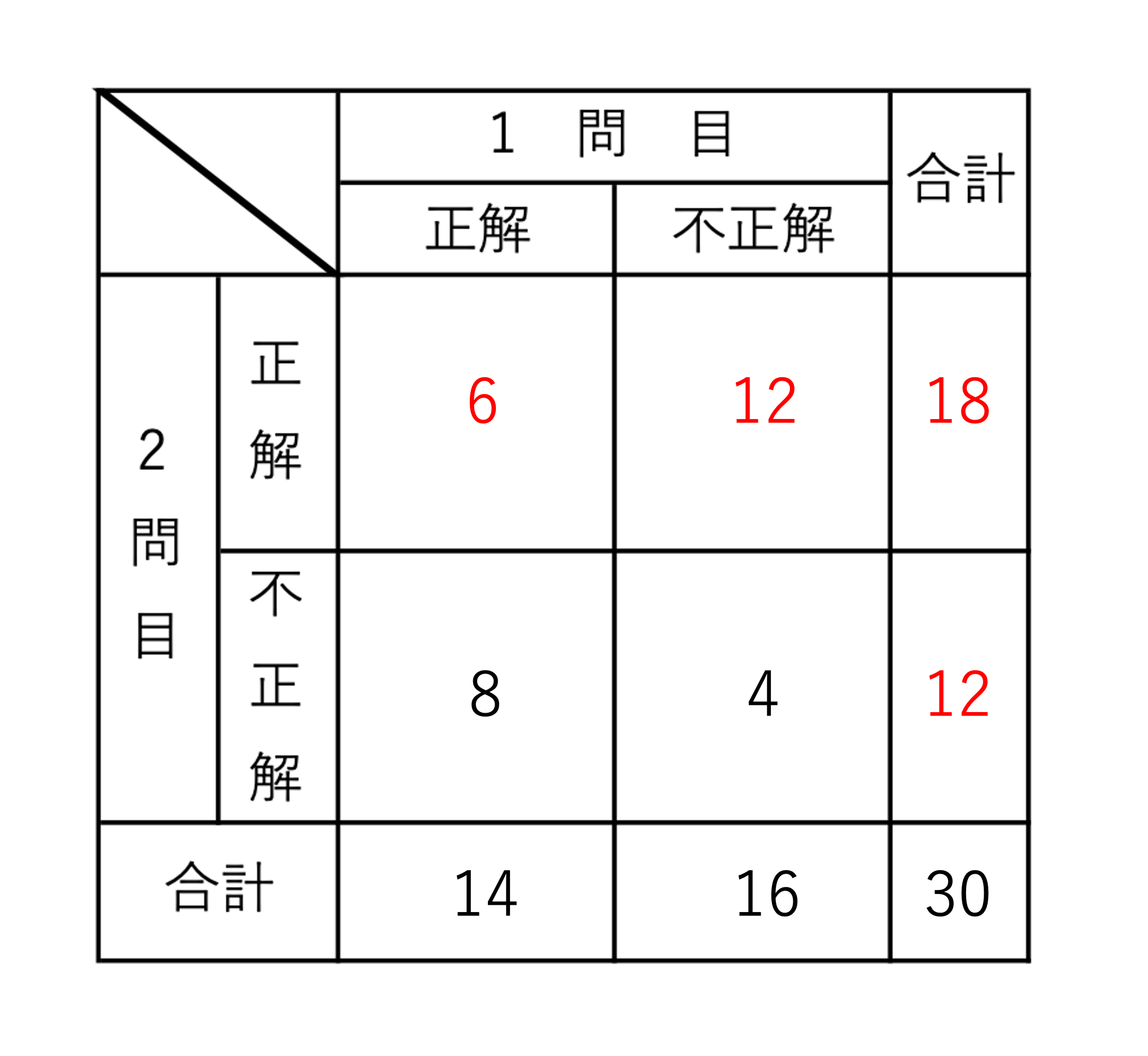
以上のように考えるとこのような表が完成します。表のスタイルだけ作ってしまえば残りは意外と簡単だ,ということがお分かりいただけたかと思います。
解き方② ベン図を作ろう!
続いてはベン図を作る方法をご紹介します。ベン図とは集合の重なり合いに注目した得方の一つです。集合というのは,いくつか集まったときに重なり合う部分があります。例えば上でご紹介した偶数・5の倍数・3桁の整数,という3つの集合において,100という数字が全てのグループに該当していました。そのため集合の図は実は下のように整理できるのです。
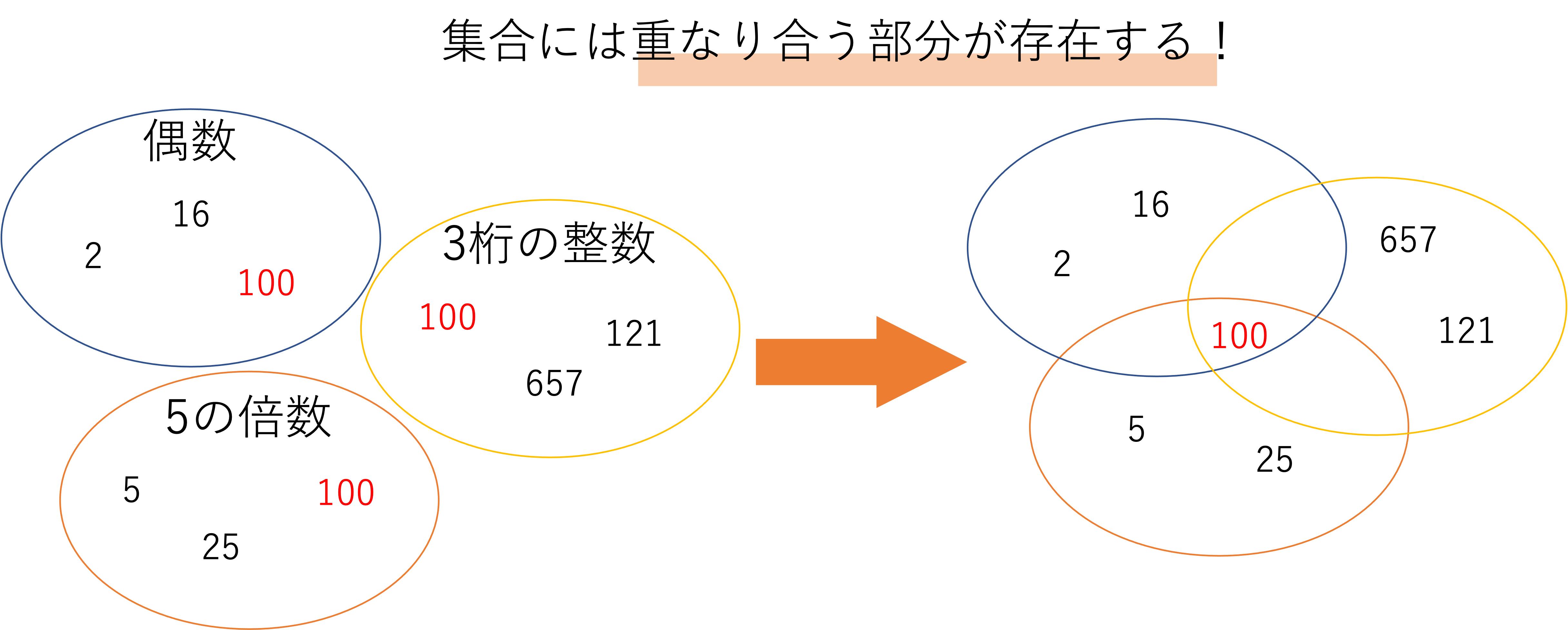
ちなみに100という数字は全てに当てはまっていましたが,2つに当てはまるけど残りの1つには当てはまらないものもあります。10などがいい例でしょう。10は偶数かつ5の倍数ですが,3桁ではないですよね。その他だと105などが,5の倍数かつ3桁だけど偶数ではない数として挙げられます。
そしてこの集合の重なり合いを1問目・2問目という軸に沿って表せば,今回の問題を解く手がかりにできますね。まずは大まかな書き方をご紹介します。ベン図とは長方形と円とで構成されます。長方形が全体を表し,それぞれの円が前述した軸に対応しています。今回のクラス全体,そして1問目・2問目という軸を表現すると次の図のようになります。

この図を作ることで,4つのグループが視覚的にわかりやすくなります。長方形の内側で2つの円の外側にある部分は2問とも不正解の人,2つの円が重なる部分は2問とも正解の人,左の円だけに含まれる部分は1問目だけ正解の人,右の円だけに含まれる部分は2問目だけ正解の人を表します。

この図を基に問題を解いていきます。といっても,後は表を使った解き方と同じように数字を埋め込んでいけばいいですね。同じ要領なので大部分は省略しますが,まずは問題文に出てきた数字を書き込みましょう。
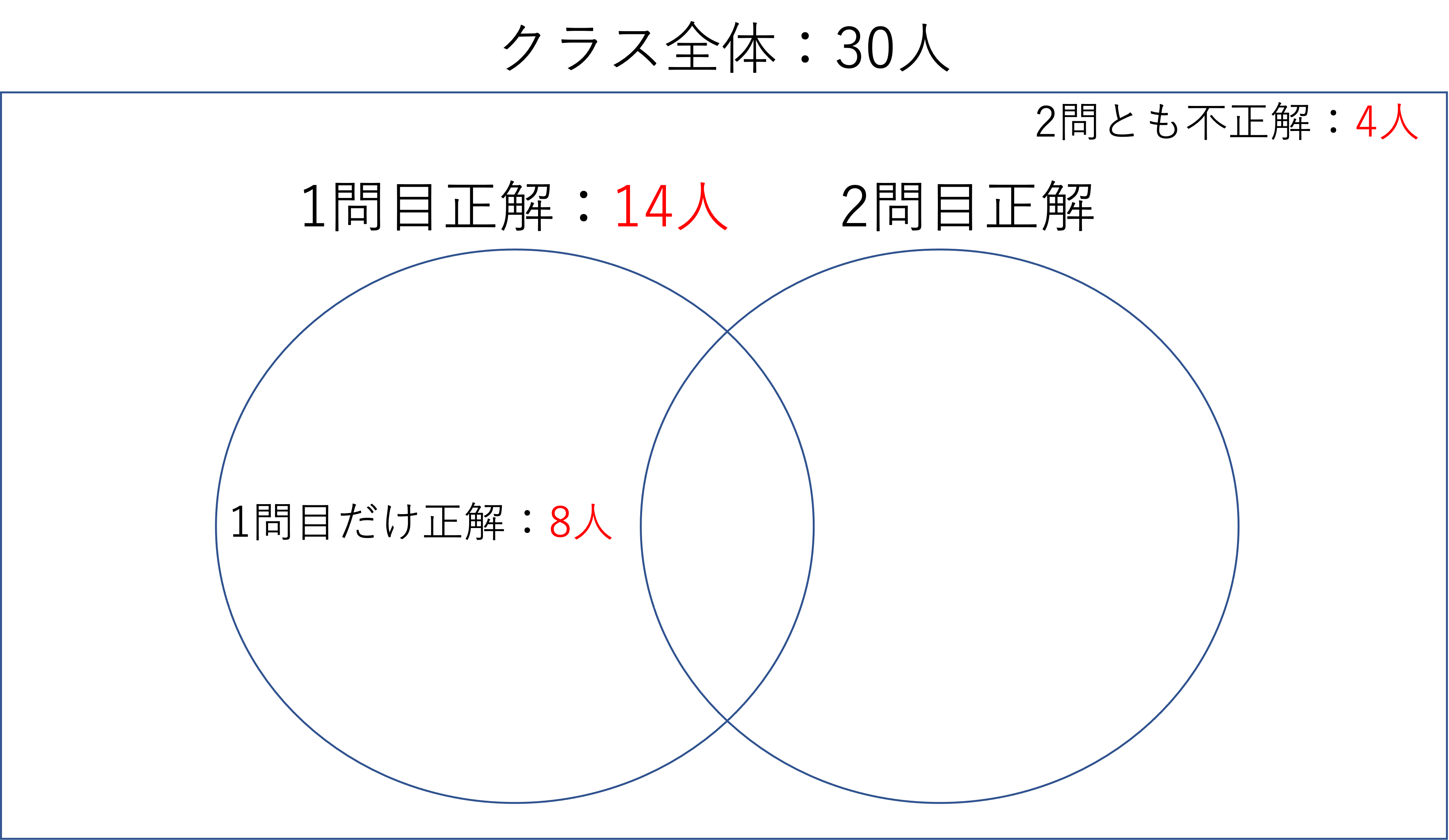
そして残りの空欄,今回だと2問とも正解の部分と2問目だけ正解の部分を埋めていきましょう。まず2問とも正解の人の数ですが,これは1問目正解の部分に注目すると求められますね。いま1問目に正解した人の合計は14人で,うち8人は2問目で不正解でした。ということは,残った14-8=6人は両方ともに正解した人だとわかります。
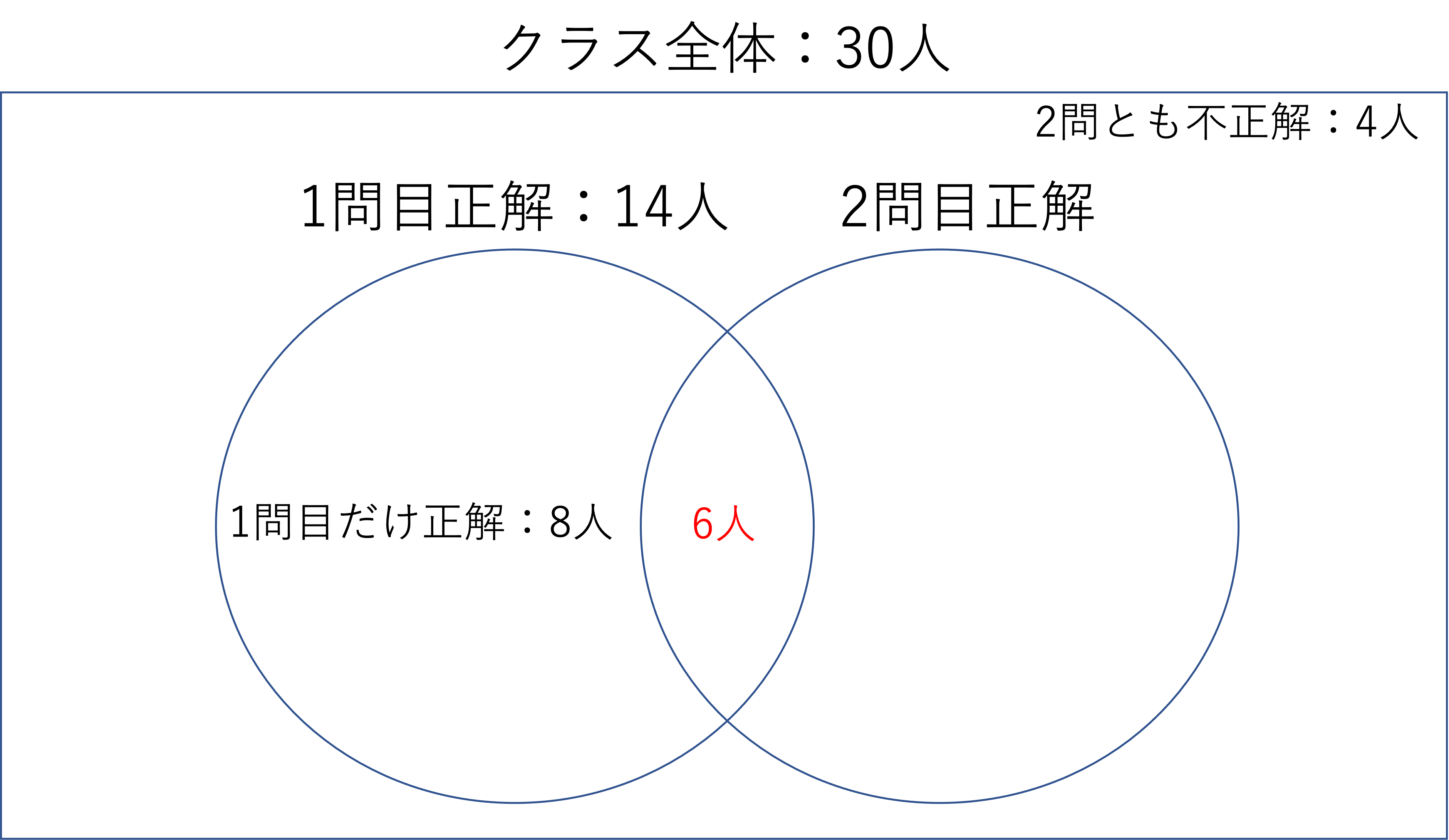
では残った2問目だけに正解した人の数を求めましょう。この部分を求めるためには,まず1問目の結果にかかわらず2問目に正解した人の数を計算しなければいけません。しかし,これもベン図を使えば一発でわかります。2問目に正解した人,つまり右の円に属する人の数は,全体の長方形から,両方に不正解だった人と1問目にだけ正解した人の数を引くことで求められます。つまり30-(4+8)=18人だということです。そしてこのうち6人が両方に正解したということでしたので,18-6=12人が2問目だけに正解した人だ,ということですね。
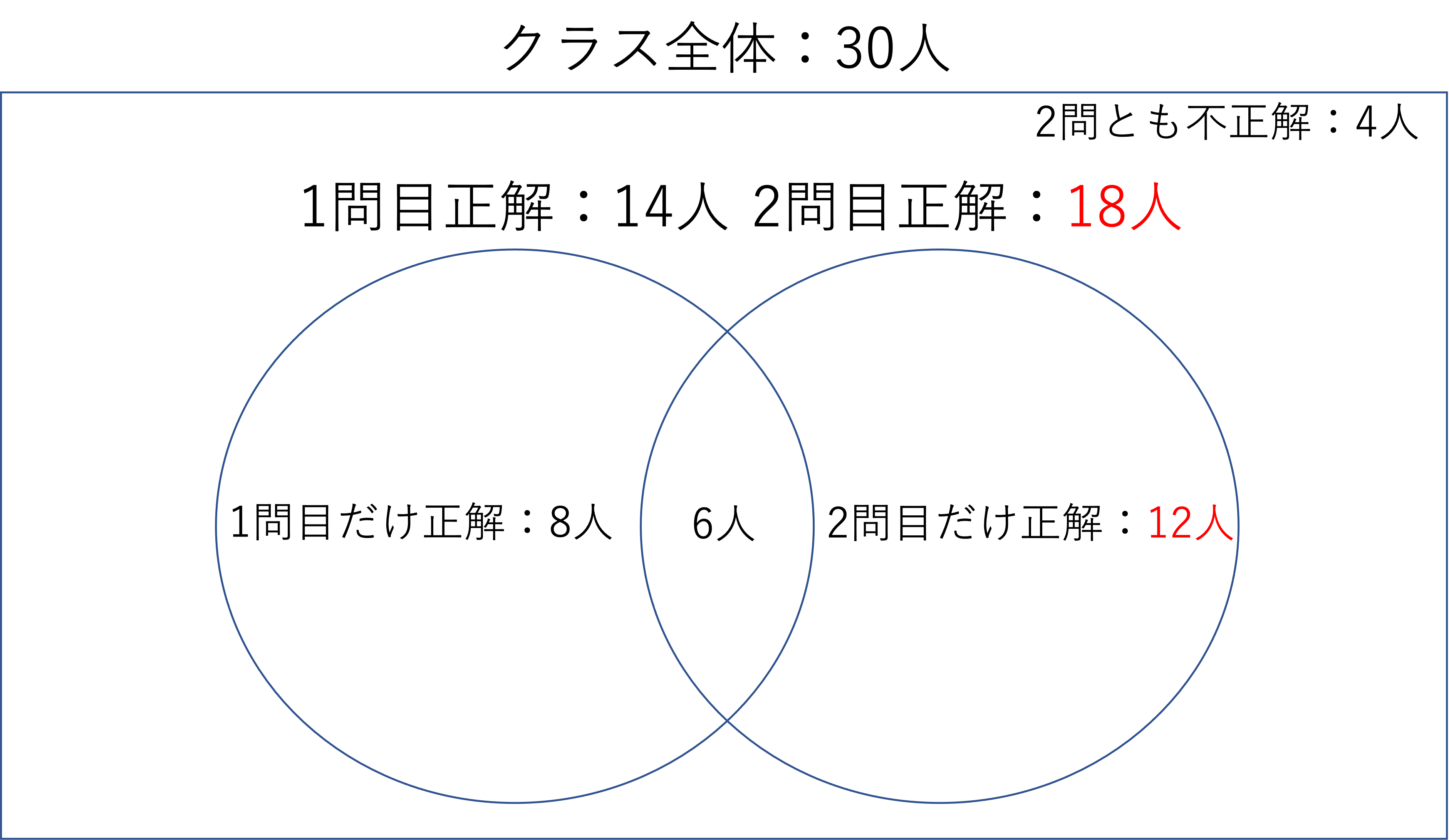
以上のように考えるとこのような図が完成します。図形が何を表すか,に最初のうちは戸惑うかもしれませんが,慣れてしまえば計算の数は表を作るより少なく済みます。考え方はこちらもパズルと一緒なので,難しく考えすぎないことがコツですね。
それぞれのメリットとデメリット!
2つの解き方を紹介したところで,「表を作ったらいいのかベン図を作ったらいいのかどっちなの?」と感じる人もいるでしょう。そこで,最後にそれぞれの方法のメリットとデメリットをご紹介して締めくくります。
まず表を作る方法についてですが,こちらは何といっても馴染み深いことがメリットとして挙げられるでしょう。1年生のころから色々なシーンで表を使ってきたことから,悩まずに作成・計算ができることが強みです。しかし,計算するところがやや多いことがデメリットとして存在します。もちろんベン図の方でも計算が必要になるためさして変わらないようにも思えるでしょうが,一刻を争う中学受験では遅れを取る一因となる可能性があります。
他方ベン図を作る方法については,計算や作図が楽なことがメリットとして挙げられるでしょう。□と○を書いて作図は完成,6箇所に数字を書き込めば計算も終わり,とスムーズに進められれば大幅な時間短縮が見込めます。しかし,書き方への慣れが必要なことがデメリットとして存在します。慣れていないとむしろ計算が長引いたり正しい答えを導き出せなかったりします。
そのため,受験まで余裕がある人はベン図をたくさん書いて慣れていくことを,余裕が無かったり他の科目・単元に力を入れたかったりする人は表を書いて完結させることをオススメします。参考にしてみてください。
まとめ
今回の記事では集合算の解き方について取り扱いました。冒頭でも述べたように,集合算というのは本来高校で習う単元であるため,もしかしたら理解が難しいかもしれません。しかし本質を理解できなくても,解き方そのものは遊び感覚で身に付けられると思いますので,ぜひこの記事を参考に理解を深めていただけますと幸いです。次回の記事では問題集形式で集合さんの解き方に慣れよう,という内容を扱う予定ですので,そちらもご参考ください。
(ライター:大舘)