理科の化学分野,水溶液についての問題の1つに再結晶についてのものがあります.
再結晶の問題は,水溶液の濃度や溶解度についてしっかり理解していることが前提となります. 計算も小数の数字を多く扱うことになるため,間違いや計算ミスが多くなる傾向があります.
しかし水溶液について理解しておくことは理科の勉強について非常に重要なことです.基礎がしっかり理解できていれば,計算が複雑な問題であっても解くことができます.
ここでは再結晶の問題について,その考え方や解き方を丁寧に紹介していきます.
Contents
再結晶の問題の解き方
まずは再結晶について簡単に復習しましょう.
実際に問題を解く前に,まずはしっかり復習しておきたいという方は,下の記事を参考にしてください.
『溶解度と再結晶 ~物質が水に溶ける量には限界があることや、それを利用した綺麗な物質の回収方法について知ろう~』
https://chugaku-juken.com/solubility-recrystallization/
再結晶は,温度が高いことで溶質が多く溶けている水溶液から,水溶液の温度を下げることで溶解度を下げて,溶けきれなくなった溶質が出てくるようにする操作です.
溶けきれなくなった分だけが出てくるわけですから,水溶液に溶けていた溶質の全てを回収できるわけではありません.
ここで,回収できる溶質の重さが何gかを求める問題が多く出てきます.
まずは実際に出てくる問題の例を見てみましょう.
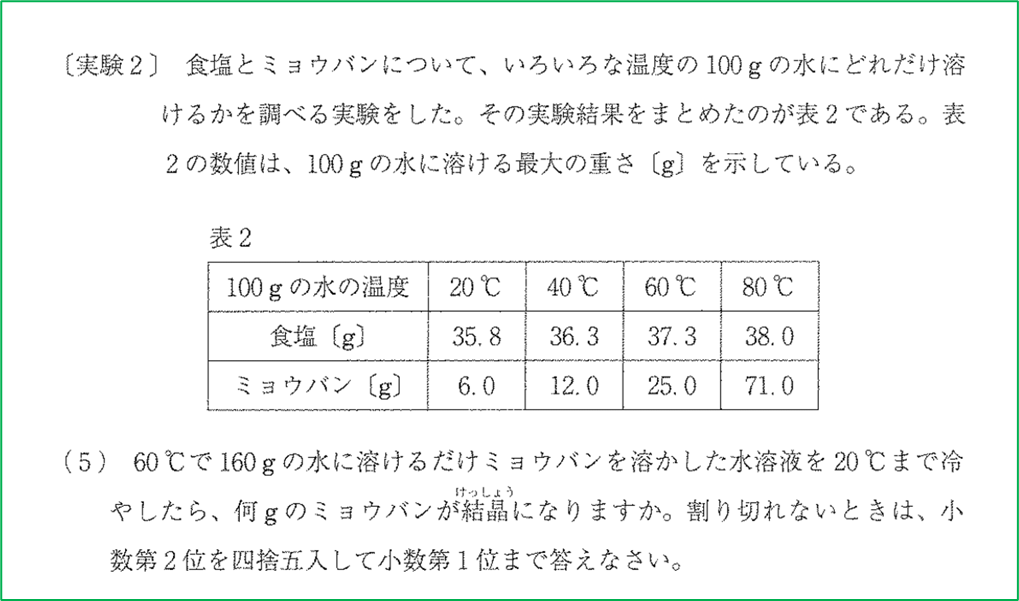
① まず温度が高い状態で溶質が何g溶けているかを考える
まずは,水溶液の中に溶質(ここではミョウバン)が何g存在しているのかを知るのが第一です. これを知ることで,最大何g出てくる可能性があるのかをまずは明らかにします.
溶媒の温度が高いときに,溶質が何g溶けているかを確認しましょう.
ほとんどの場合は,この問題のように,温度が高い水に最大まで溶かしてあり,溶解度から溶質の重さを計算させる場合が多いです。
しかし,必ずしも最初の状態が飽和水溶液になっている,つまり限界まで溶質を溶かしたとは限りません.
必ず問題文をよく読んで,溶質が何g溶けているのかをハッキリさせましょう!
ここでは問題のように,最初の状態が飽和水溶液の場合について解説していきます.
ここでは最初に「□℃で〇gの水に(ミョウバンを)溶かせるだけ溶かした水溶液」があります.
この場合,溶けている溶質の量は直接書かれていません.
つまり,溶けているミョウバンの重さを,自分で計算して明らかにする必要があります.
ここでポイントになるのが「溶解度」です. 溶解度の値を使うことで,飽和水溶液に溶けている溶質の量を計算することができます。
ここで溶解度について簡単におさらいしておきましょう.
溶解度とは,「100gの水に溶ける最大の重さ(g)」のことです. この問題では表に書かれている値のことになります.
温度の違いによって溶解度,つまり溶ける最大の重さが変わる点にも注目です!
それでは実際に,この溶解度の値を使って,水溶液の中に溶けているミョウバンの重さを計算してみましょう.
ここで溶解度について,もう1つの性質が重要になります.
それは「水に溶ける最大の量は,元の水の量に比例する」という点です.
つまり今,100gの水に最大で10gまで溶ける物質があると考えてみましょう.
元々の水が,2倍の量である200gあったとすると,この物質は,200gの水に,10gの2倍の20gまで溶かすことができます.
逆に,もともとの水が,100gの半分の50gしかなかったとすると,この物質は,10gの半分の5gまでしか,50gの水に溶かすことができません.
これを踏まえて,60℃の水160gに,ミョウバンが最大で何gまで溶かせるかを考えていきましょう.
今,水は60℃なので,ミョウバンの60℃における溶解度を確認します.
表2から,ミョウバンは60℃の水100gに25.0gまで溶かすことができると分かります.
これが60℃の水に対するミョウバンの溶解度となります.
そして今,水は160gあり,これは100gの1.6倍です.
つまり,水160gに溶けるミョウバンの最大の量は25.0gの1.6倍になるはずです.
よって水160gに溶けるミョウバンの最大の量を計算すると次のようになります.
25.0×1.6=40.0
つまり,今問題では,水160gの中に,ミョウバンが40g存在していることになります.
これで,温度が高い状態での水の中に溶けている溶質の量が分かりました.
② 温度を下げたときの水の量を考える
次に考えるのは,水溶液の温度を下げた時点で,溶媒としての水がどれだけ残っているかを考えます.
何を言ってるのかと思う方もいるかもしれませんが,問題によってはまず水を蒸発させることで水の量を減らすこともあります.
再結晶では水に溶け残る分の溶質が必ず出てきます.
だからこそ,溶け残る分の溶質の量を知るために,まずは溶かしている水の量をしっかり把握するのです.
問題をよく読んで,最初の水の量と,最終的な水の量をしっかり把握しましょう.
この問題では,水の量は温度が高い状態と低い状態で変化していないため,160gのままとなります.
③ 最終的な水の条件で溶質が最大どれだけ溶けるかを考える
次に考えるべきことは,冷やした後の,最終的な水の条件で溶質が最大どれだけ溶けるかを考えます.
ここで求める溶質の量は,再結晶の操作をしても,水に溶けたままで出てこない量となります.
この問題については,冷やした後の水の条件は,20℃で160gの水となります.
ここに溶けるミョウバンの最大の量を考えましょう.
考え方は①と同じです. まずは20℃の水におけるミョウバンの溶解度から考えていきましょう.
表2より,ミョウバンは,20℃の水100gに対して,最大6.0gまで溶けます.
そして今,水は160gあるので,ここには最大何gまで溶けるかを考えます.
溶質が溶ける最大の量は,水の量に比例し,水は100gの1.6倍の160gあるので,20℃の水160gに溶けるミョウバンの最大の量は,次のように計算できます.
6.0×1.6=9.6
よってミョウバンは20℃の水160gに対して,最大9.6gまで溶けます.
これで溶け残る分の溶質の量を計算することができました.
④ 再結晶によって出てくる溶質の量を計算する
それでは最後に,再結晶によって出てくる溶質の量を計算しましょう.
ここでは最初に出した,「温度が高い状態の溶媒に溶けている溶質の量」と,「温度が低い状態の溶媒に溶け残る溶質の量」の差を考えます.
これは最初に溶けていた溶質の量のうち,温度の低い溶媒の中に溶け残らずに出てくる量を求めることになります.
つまり,①で求めた量と,③で求めた量の差を考えればいいのです.
最初に水溶液の中にあったミョウバンは40gであり,温度を下げた状態の水に溶けるミョウバンの最大の量は9.6gだから,再結晶によって出てくるミョウバンの量は次のように計算できます.
40-9.6=30.4
したがって,この問題の答えは30.4gとなります.
ここまでの流れをまとめてみましょう.
- まず温度が高い状態で溶質が何g溶けているかを考える
- 温度を下げたときの水の量を考える
- 最終的な水の条件で溶質が最大どれだけ溶けるかを考える
- 再結晶によって出てくる溶質の量を計算する
くり返し復習して,再結晶の問題もしっかり得点源にしていきましょう.
入試実践演習
それでは,上で学んだことを活かして,実際の入試問題2つに挑戦してみましょう.
ただし,上の考え方に加えて少し考えないとどちらも正しく解けないので気を付けて解きましょう.
問題1
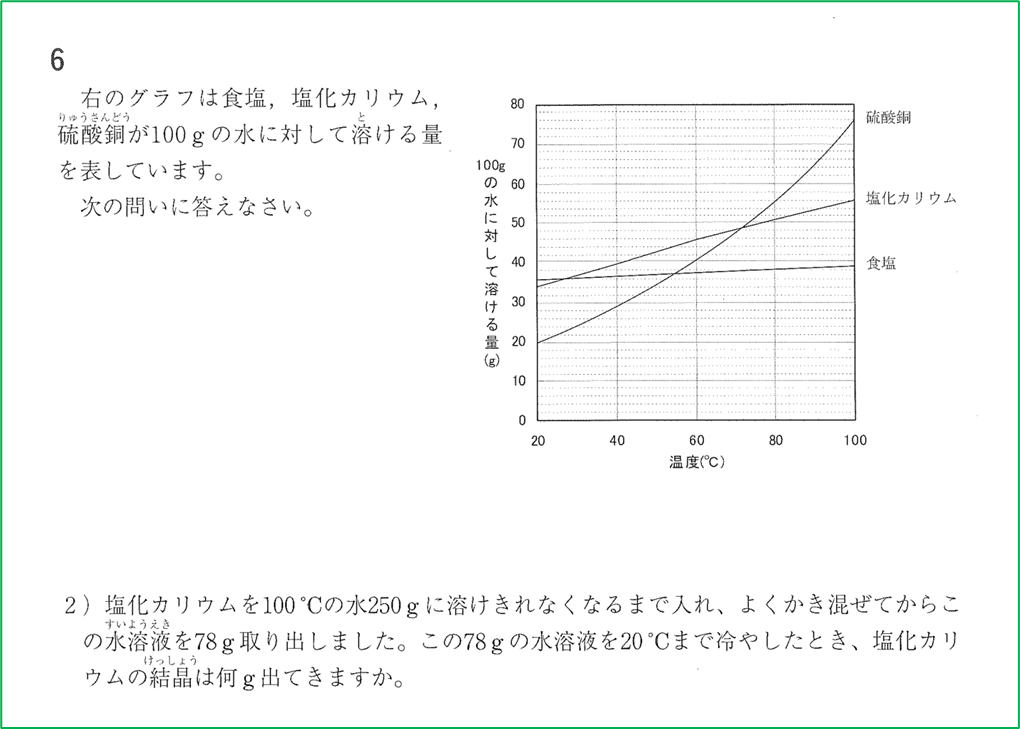
解説
まずは100℃の水250gに溶ける塩化カリウムの最大の量を考えましょう.
この問題の場合,溶解度はグラフで書かれているので,ここから読み取る必要があります.
グラフにおける塩化カリウムの曲線の100℃のところを見ると,塩化カリウムは,100℃の水100gに56g溶けることが読み取れます.
これを水250gは100gの2.5倍だから,100℃の水250gに溶ける塩化カリウムの最大の量は,
56×2.5=140
つまり,問題の最初に溶かした塩化カリウムの量は140gということになります.
さて,ここから少し考える必要があります.
今,この水溶液から78gを取り出しました.
これは今作った水溶液のどのくらいの割合になるかを考えてみましょう.
まずは今できた水溶液の全体の重さを考えます.
水250gに対して140gの塩化カリウムを入れたのですから,水溶液全体の重さは,
250+140=390 より、
390gということになります.
さて78gが390gの何倍かを計算してみましょう.
78÷390=0.2
つまり,全体の0.2倍,または1/5の水溶液を取り出したことになります.
このとき,水溶液中に含まれる塩化カリウムの量も,元の140gの0.2倍だけ取り出されたことになります.
つまり取り出された水溶液に含まれる塩化カリウムの量は,
140×0.2=28
よって水溶液78gのうち,28gは塩化カリウムの重さです.
ここで同時に,残りの重さ,
78-28=50より,
78gのうち50gは水の重さということになります.
これを20℃まで冷やします.
水の量は50gですから,次に冷やした後の20℃の水50gに溶ける塩化カリウムの最大の量を考えます.
グラフにおける塩化カリウムの曲線の20℃のところを見ると,塩化カリウムは,20℃の水100gに34g溶けることが読み取れます.
そして今,水50gは100gの0.5倍だから,ここに溶ける塩化カリウムの最大量は次のように計算できます.
34×0.5=17
よって,塩化カリウムは,20℃の水50gに最大17gまで溶けます.
冷やす前にあった塩化カリウムの量は,上で計算した通り28gですから,17gとの差をとると,
28-17=11より,
出てくる塩化カリウムの量は11gとなることが分かります.
問題2
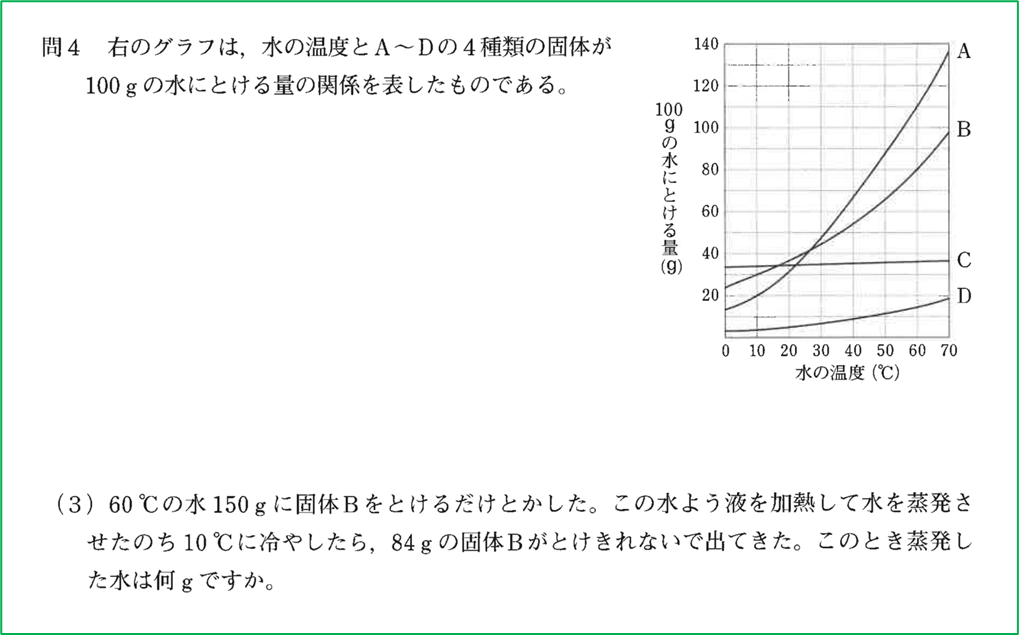
解説
こでは出てくる溶質の量ではなく,途中で蒸発させた水の量を考えます.
全体の流れは上で説明したものと同じように考えて,逆算すればいいのです.
まずは順番に考えていきます.
今,60℃の水150gに固体Bを最大まで溶かすことを考えます.
問題のグラフより,60℃における水への固体Bの溶解度は80gであることが分かります.
つまり,固体Bは,60℃の水100gに対して80gまで溶けます.
水150gは,100gの1.5倍だから,
80×1.5=120より,
この問題では,固体Bを,60℃の水150gに120g溶かしたことになります.
さて,ここで蒸発させた後の水の量が分からないので,今度は後ろから考えましょう.
この水溶液から水を蒸発させた後,冷やすことによって84gの固体Bが出てきました.
逆に溶け残っている固体Bの量を計算すると,
120-84=36より,
残った10℃の水の中に36gの固体Bが溶け残っていることになります.
そしてここで,これは10℃の水に最大まで溶けた状態であることに気付かなければいけません.
10℃で固体Bが最大36g溶けるためには水が何gあればいいのかを考えましょう.
グラフから,10℃の水100gに対する固体Bの溶解度を考えると,30gですから,
固体Bは10℃の水100gに対して,最大30g溶けることが分かります.
ここで,水に溶ける溶質の最大量は水の量に比例することを利用すると,固体Bが最大36g溶ける水の量を計算することができます.
36gが30gの何倍かを考えます.
36÷30=1.2より,
36gは30gの1.2倍だから,今冷やした後の水の量は,
100×1.2=120より,
120gであることが分かります.
つまり,蒸発することで減っている水の量は,
150-120=30より,
30gであることが分かります.
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

まとめ
再結晶の問題を解く基本的なポイントを改めて確認します.
- まず温度が高い状態で溶質が何g溶けているかを考える
- 温度を下げたときの水の量を考える
- 最終的な水の条件で溶質が最大どれだけ溶けるかを考える
- 再結晶によって出てくる溶質の量を計算する
問題2のように,途中の値を出す時には,最後から逆算するとよいでしょう.
水溶液や再結晶の問題は複雑であり,苦手なイメージが持たれやすいですが,その考え方を理解すれば解き方が見えてくるはずです.
必要に応じて図やグラフをうまく活用しながら,正確に解けるように繰り返し練習しましょう.