皆さんは「カロリー計算」と聞いてどのようなことを思い浮かべるでしょうか? 「カロリー」といえば、お菓子の袋のうらに書いてあったりするあれが思い浮かべやすいのではないでしょうか? では、この「カロリー」とは何かを説明できることはできるでしょうか。身近な言葉ではありますが、カロリーとは何なのか、考えたことのある人は少ないと思います。
今回はそんな「カロリー計算」について解説していきます! 分野としては「熱の移動と温度変化」にあたりますね。主に水の温度を上昇させるのにどの程度のカロリーが必要になるのか計算させるような問題が多く出題されています。
「熱の移動と温度変化」の分野に関しては、必ずしも頻出の内容とは言えないので、電球やてこの問題に比べて、これまであまり勉強してこなかったという人も多いと思います。熱量を計算する以前の基礎的な内容に関しては、以下の記事でも解説していますので、興味のある人は参考にしてください。
今回の記事では以下のことを解説します。
- 「カロリー」とはエネルギー(熱量)の単位のこと
- \(1\,\mathrm{cal}\) =(水\(1\,\mathrm{g}\)を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要なエネルギー)
- 熱が2つの物体の間のみを移動するとき(物体Aが失った熱量)=(物体Bが得た熱量)
- 物体を同じように加熱する時間と、物体が得る熱量は比例する
最後には練習問題も用意していますので、カロリー計算について基礎を理解することができたら、問題を解いて知識をアウトプットしていきましょう! それでは解説に入ります。
Contents
カロリーとは何か? 具体的なイメージをつかもう!
カロリーと食品の関係
「カロリー」と聞くと食品を思い浮かべますよね。このカロリーとはいったい何なのでしょうか?
厚生労働省が策定する「日本人の食事摂取基準」によれば、カロリーはエネルギーの単位とあります。生き物は、エネルギーを体外から摂取し、最終的に熱として身体から放出しています。このエネルギーや熱量のもとになるのが主に食品であり、食品を体内に摂取したときのエネルギー量をカロリーという単位で表示しているということです。ちなみに、エネルギーは\(\mathrm{J}\)(ジュール)という単位が使われることが多いですが、食品などには\(\mathrm{kcal}\)(キロカロリー)が使われることが慣習になっています。エネルギーと熱量は同じものと考えて良いですが、熱量といったときにはカロリーの単位を使うことが多いことに注意しましょう。
これも余談ですが、カロリーとは単に単位を指すので、「カロリー計算」ではなく、「熱量計算」という方が正確なのでしょう。もっとも、一般的に「カロリー計算」とよばれているので、間違いではないと思いますが……

1カロリーはどれくらいの量?
さて、「カロリー計算」というくらいですから、熱量には具体的な値があります。それは、次のように求められます。
\(1\,\mathrm{cal}\) =(水\(1\,\mathrm{g}\)を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要なエネルギー)
たとえば、\(500\,\mathrm{g}\)の水の温度を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要な熱量と\(250\,\mathrm{g}\)の水の温度を\(2\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要な熱量は同じです。
水以外の物体ではこの計算式は成り立たないので注意しましょう。\(1\,\mathrm{g}\)の鉄の温度を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要な熱量は\(1\,\mathrm{cal}\)ではありません。一般に、ある物質\(1\,\mathrm{kg}\)の温度を\(1\,\mathrm{C}^\circ\)あげるのに必要な熱量のことを「比熱」とよびます。比熱の大きい物体ほど、温度を上昇させるのに必要な熱量が大きいので、「温まりにくい」物質といえます。水の比熱は\(1\,\mathrm{kcal}\)です。ちなみに、鉄の比熱は水の10分の1ほどなので、水よりも「温まりやすい」物質といえます。
以上のことを具体的な計算式であらわすと、以下のようになります。
\(\text{水が得た(失った)熱量}\,\mathrm{cal} = \text{水の重さ}\,\mathrm{g} \times \text{温度変化}\,{}^\circ\mathrm{C} \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} \)
この式は熱量計算で何度も使うことになります。注意するのは「温度」ではなく「温度変化」となっている点です。物質が\(30\,{}^\circ\mathrm{C}\)から\(40\,{}^\circ\mathrm{C}\)に変化するのと、\(80\,{}^\circ\mathrm{C}\)から\(90\,{}^\circ\mathrm{C}\)に変化するのとでは同じ熱量しか移動しないということです。
熱量に関する重要な事実
2つの物体AとBの間で熱が移動し、Aの温度が低下し、Bの温度が上昇するとき、次のような関係が成り立っています。
(物体Aが失った熱量)=(物体Bが得た熱量)
この関係式はカロリー計算の問題を解くときに必要となりますので、しっかりと理解しておきましょう。「熱」や「熱の移動」を直接観測することはできませんが、「熱量」の値の変化は物体の温度を測定することで明らかになります。
外からヒーターで加熱したり、熱が空気中に逃げてしまったりしない限りはこの関係は成り立ちます。この、移動した熱量(エネルギー)の値は同じという事実は非常に重要なので、ぜひ覚えておきましょう。
また、次の事実も重要です。物体(多くは水)に熱量を与える問題では、物体を加熱するという方法をとることが多いです。そこで、物体を同じように加熱する時間と熱量の関係を考えましょう。それは、次のようになります。
物体を同じように加熱する時間と、物体が得る熱量は比例する
つまり、加熱時間を2倍、3倍……と変化させたとき、熱量も2倍、3倍……と増えていくということです。もちろんこれは「同じように」加熱したという条件付きであり、途中で加熱するためのエネルギーを大きくするなどの変化を加えた場合は熱量と加熱時間は変化しません。
練習問題をといてカロリー計算をマスターしよう!
では、これまで勉強した知識を使って練習問題を解いてみましょう。一度で解くことができなくても、何度も挑戦して記憶を定着させることが重要です!
問題1
(1) \(300\,\mathrm{g}\)の水を加熱したところ、温度が\(30\,{}^\circ\mathrm{C}\)上昇しました。このとき、水が得た熱量は何\(\,\mathrm{cal}\)ですか。このとき熱は水以外の物体に移動しないものとする。
(2) \(300\,\mathrm{g}\)、\(90\,{}^\circ\mathrm{C}\)の水を放置しておいたところ、水の温度が\(60\,{}^\circ\mathrm{C}\)になっていました。このとき、水が失った熱量は何\(\,\mathrm{cal}\)ですか。
(3) \(300\,\mathrm{g}\)、\(50\,{}^\circ\mathrm{C}\)の水に\(1500\,\mathrm{cal}\)の熱量を与えました。このとき、水の温度は何\(\,{}^\circ\mathrm{C}\)になりますか。このとき熱は水以外の物体に移動しないものとする。
(4) \(300\,\mathrm{g}\)、\(30\,{}^\circ\mathrm{C}\)の水を\(45\,{}^\circ\mathrm{C}\)になるまで1分間温めました。このとき、水が得た熱量は何\(\,\mathrm{cal}\)ですか。このとき熱は水以外の物体に移動しないものとする。
(5) (4)と同じような方法で\(300\,\mathrm{g}\)、\(30\,{}^\circ\mathrm{C}\)の水を30秒間温めました。このとき、水の温度は何\(\,{}^\circ\mathrm{C}\)になりますか。
解説
(1) カロリーの定義を思い出しましょう。「水\(1\,\mathrm{g}\)を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要なエネルギー」が\(1\,\mathrm{cal}\)です。この定義から、水の量が多ければ多いほど、上昇する温度が高ければ高いほど、必要な熱量は大きくなることがわかりますね。(1)を計算式にあらわすと、
\(300\,\mathrm{g} \times 30\,{}^\circ\mathrm{C} \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 9000\,\mathrm{cal}\)
と答えが求まります。ここで、\(1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}}\)と書いたのは、先ほども紹介した水の比熱です。この水の比熱を省略して書く場合も多いですが、重さと温度が熱量に変わるのをわかりやすくするために、この記事では毎回書くことにします。
(2) この問題では、熱が空気(や水の入れ物)に逃げている状況をあらわしています。熱量の計算では「温度」ではなく、「温度変化」を計算に使うということを紹介しましたね。ここでも温度変化を考えて、
\(300\,\mathrm{g} \times (90\,{}^\circ\mathrm{C} – 60\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 9000\,\mathrm{cal} \)
と答えを求めることができます。
(3) これまでの問題は、熱量を求める問題でしたが、今度は水を求める問題です。熱量の計算式では「温度変化」しか求めることができませんので、まず「温度変化」を求めた後、もとの「温度」と合計して、最終的な「温度」を計算します。温度変化を□\(\,{}^\circ\mathrm{C}\)とすると、
\(300\,\mathrm{g} \times \text{□}\,{}^\circ\mathrm{C} \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 1500\,\mathrm{cal} \)
となります。したがって、温度変化は
\(\text{□} = 5\,{}^\circ\mathrm{C}\)
となります。もとの温度が\(50\,{}^\circ\mathrm{C}\)だったので、求める温度は
\(50\,{}^\circ\mathrm{C} + 5\,{}^\circ\mathrm{C} = 55\,{}^\circ\mathrm{C}\)
となります。
(4) 再び基本的な問題です。熱量の計算式を使うと、
\(300\,\mathrm{g} \times (45\,{}^\circ\mathrm{C} – 30\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 4500\,\mathrm{cal} \)
と求めることができます。
(5) この問題は、「物体を同じように加熱する時間と、物体が得る熱量は比例する」という関係式を使います。(4)で、水を1分間加熱したときに得た熱量は\(4500\,\mathrm{cal}\)でした。いま、水の量、加熱する前の温度、加熱の仕方のすべてが同じ条件で、加熱時間だけが半分になっています。したがって、
\(4500\,\mathrm{cal} \div 60\,\text{秒} \times 30\,\text{秒} = 2250\,\mathrm{cal}\)
と求めることができます。
最後に、問題文の「熱は水以外の物体には移動しないものとする」という文言の意味について考えてみましょう。もし、水以外の物体(例えば空気中)に熱が移動してしまった場合、どうなるでしょうか。例えば、\(300\,\mathrm{g}\)の水に\(9000\,\mathrm{cal}\)の熱量を与えたとき、このうちの\(1500\mathrm{cal}\)が空気に移動したとしましょう。熱が空気に逃げなければ
\(9000\,\mathrm{cal} \div 300\,\mathrm{g} \div 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 30\,{}^\circ\mathrm{C}\)
だけ温度が上昇するところですが、実際は
\( (9000\,\mathrm{cal} – 1500\,\mathrm{cal}) \div 300\,\mathrm{g} \div 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 25\,{}^\circ\mathrm{C}\)
だけしか温度が上がりません。つまり、水以外に熱が移動してしまうとそもそも問題を解くことができなくなってしまうため、このような文言がついているのです。熱が水以外の物体に移動しないようにするためには、例えば発泡スチロールなどの断熱材の容器を使って実験をする必要があります。実際に水以外の物体に熱を移動させないということは難しいですが、問題では実際の環境よりも解きやすさが優先されているのです。
問題2
以下の問題では、熱は水以外の物体には移動しないものとする。
(1) \(300\,\mathrm{g}\)、\(30\,{}^\circ\mathrm{C}\)の水と、\(100\,\mathrm{g}\)、\(70\,\mathrm{g}\)の水を混ぜました。このとき、水の温度は何\(\,\mathrm{g}\)になりますか。
(2) \(300\,\mathrm{g}\)、\(30\,{}^\circ\mathrm{C}\)の水に、\(200\,\mathrm{g}\)で温度のわからない水を混ぜました。このとき、水の温度が\(50\,{}^\circ\mathrm{C}\)になりました。加えた水の温度は何\(\,\mathrm{g}\)でしたか。
(3) \(100\,\mathrm{g}\)、\(90{}^\circ\mathrm{C}\)の水に、\(30\,{}^\circ\mathrm{C}\)で量のわからない水を混ぜました。このとき、水の温度が\(70\,{}^\circ\mathrm{C}\)になりました。加えた水の量は何\(\mathrm{g}\)でしたか。
解答
問題2では問題1では出てこなかった、「2つの物体同士の熱の移動」をあつかっています。この場合で重要なのは、
(物体Aが失った熱量)=(物体Bが得た熱量)
という考え方です。このことを念頭に問題を解いてみましょう。
(1) 2種類の温度の水が用意されています。それぞれ移動した熱量を求めてみましょう。混ぜ合わせたあとの水の温度を□\(\,{}^\circ\mathrm{C}\)とすると
\(30\,{}^\circ\mathrm{C}\)の水……\(300\,\mathrm{g} \times (\text{□}\,{}^\circ\mathrm{C} – 30\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 300\times(\text{□}-30)\,\mathrm{cal}\)
\(70\,{}^\circ\mathrm{C}\)の水……\((100\,\mathrm{g} \times (70\,{}^\circ\mathrm{C} – \text{□}\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 100\times (70-\text{□})\,\mathrm{cal}\)
となります。したがって、2つの水の間で移動した熱量は同じなので、
\(300\times(\text{□}-30)\,\mathrm{cal} = 100\times (70-\text{□})\,\mathrm{cal}\)
となります。したがって、2つを混ぜ合わせたときの温度は
\(40\,{}^\circ\mathrm{C}\)
と求めることができます。
この計算は面積図を用いて行うことができます。
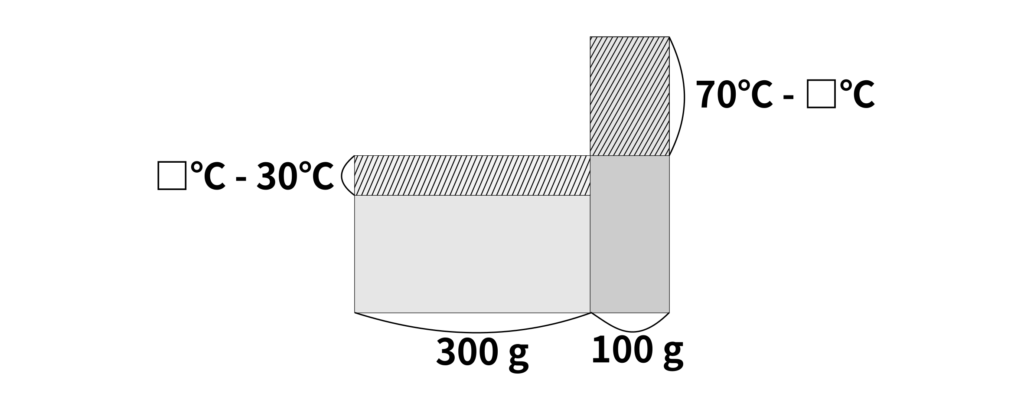
図では、2つの温度と重さをもつ水を混ぜ合わせて、等しい温度の水を作ったことを示しています。移動した熱の量は同じなので、\(30\,{}^\circ\mathrm{C}\)の水が得た熱量(左側の斜線部)と\(70\,{}^\circ\mathrm{ C}\)の水が失った熱量は同じと考えられます。これより、先ほどの計算式をみちびくことができます。
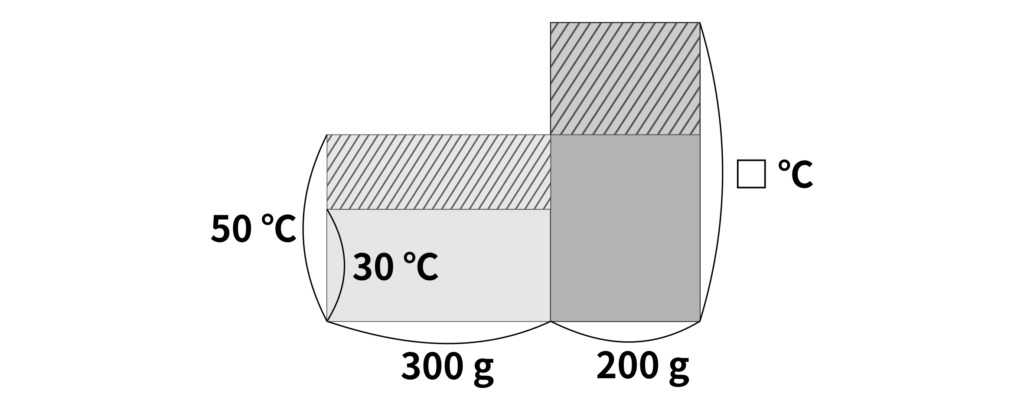
(2) この問題は、混ぜる前の水の温度がわからない状況です。加えた水の温度を□\(\,{}^\circ\mathrm{C}\)とすると、移動した熱量は
\(30\,{}^\circ\mathrm{C}\)の水……\(300\,\mathrm{g} \times (50\,{}^\circ\mathrm{C} – 30\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 6000\,\mathrm{cal}\)
\(\text{□}\,{}^\circ\mathrm{C}\)の水……\((200\,\mathrm{g} \times (\text{□}\,{}^\circ\mathrm{C} -50\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 200\times (\text{□}-50)\,\mathrm{cal}\)
となります。したがって、2つの水の間で移動した熱量は同じなので、
\(6000\,\mathrm{cal} = 200\times (\text{□}-50)\,\mathrm{cal}\)
となります。したがって、加えた水の温度は
\(80\,{}^\circ\mathrm{C}\)
と求めることができます。このときの面積図は以下の通りです。
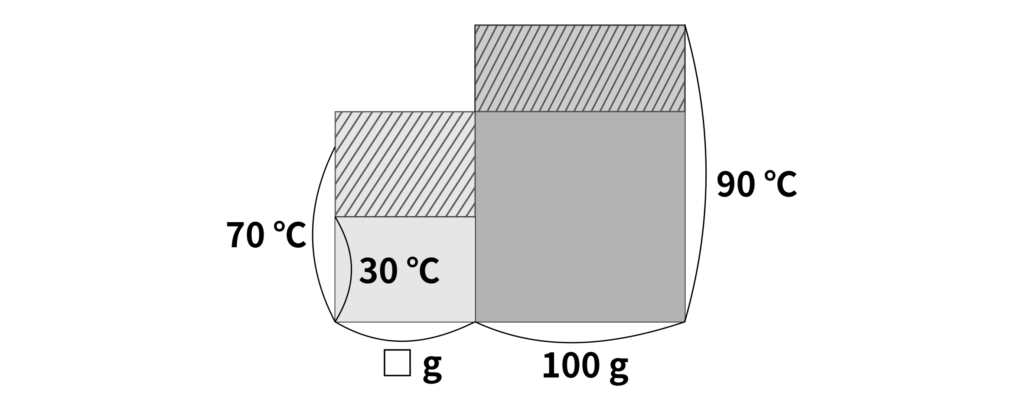
(3) この問題は、量が加えた水の量がわからない状況です。加えた水の重さを□\(\,\mathrm{g}\)とすると、移動した熱量は
\(90\,{}^\circ\mathrm{C}\)の水……\(100\,\mathrm{g} \times (90\,{}^\circ\mathrm{C} – 70\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = 2000\,\mathrm{cal}\)
\(30\,{}^\circ\mathrm{C}\)の水……\(\text{□}\,\mathrm{g} \times (70\,{}^\circ\mathrm{C} – 30\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal\,/\,\mathrm{g}\,{}^\circ\mathrm{C}} = \text{□} \times 40\,\mathrm{cal}\)
となります。したがって、2つの水の間で移動した熱量は同じなので、
\(2000\,\mathrm{cal} = \text{□} \times 40\,\mathrm{cal}\)
となります。したがって、加えた水の量は
\(50\,\mathrm{g}\)
と求めることができます。このときの面積図は以下の通りです。
問題3
図1のような装置で、\(300\,\mathrm{g}\)と\(600\,\mathrm{g}\)の水をそれぞれ加熱し、その温度変化を調べました。その結果が図2です。図2中のAとBは\(300\,\mathrm{g}\)と\(60\,\mathrm{g}\)のいずれかの加熱時間と温度変化を表わすグラフになっています。このとき、次の問題に答えなさい。
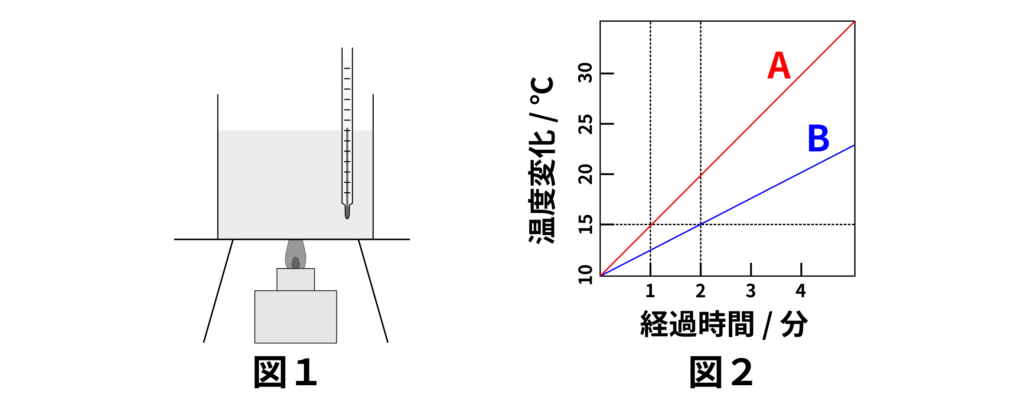
(1) \(300\,\mathrm{g}\)の水の温度上昇を表したグラフはAとBのどちらですか。
(2) \(300\,\mathrm{g}\)の水と\(600\,\mathrm{g}\)の水が同じ時間で得た熱量を比較すると、どのような関係にありますか。次のなかから選びなさい。
- \(300\,\mathrm{g}\)の水が得た熱量の方が大きい
- \(600\,\mathrm{g}\)の水が得た熱量の方が大きい
- 得た熱量はどちらも同じ
(3) 図2のAの水を10分間加熱すると何\(\,{}^\circ\mathrm{C}\)になるでしょうか。
解説
この問題は、水の温度変化と加熱時間の関係を考える問題です。応用範囲が広いとは言えないカロリー計算の問題ですが、このようなグラフを使った問題はねらわれやすいので、慣れておくとよいでしょう。
(1) この問題は水の量と温度を上げるのに必要な熱量の関係を考える問題です。カロリーの定義は
\(1\,\mathrm{cal}\) =(水\(1\,\mathrm{g}\)を\(1\,{}^\circ\mathrm{C}\)だけ上昇させるのに必要なエネルギー)
だったので、水の量が少ないほど必要な熱量が少なくなります。ここで図2を見てみると、同じ温度を上昇させるのに、Aの方はより速く温度が上昇していることがわかります。加熱の方法は同じなので、時間が短い方が水に与えている熱量は少ないです。したがって、答えは
Aのグラフ
と求めることができます。
(2) この問題は、加熱時間と熱量の関係を答える問題です。いま、水の温度について考えているのではないことに注意しましょう。同じ時間、同じ加熱方式で加熱しているので、水の量に関わらず、水が受け取る熱量は同じになります。したがって、答えは
得た熱量はどちらも同じ
となります。
(3) この問題は、図2を使って解く問題です。図2より、グラフAの水は1分間で\(5\,{}^\circ\mathrm{C}\)だけ温度上昇しています。温度変化は加熱時間に比例するので、10分間での温度上昇は
\( 5\,{}^\circ\mathrm{C} \div 1\,\text{分} \times 10\,\text{分} = 50\,{}^\circ\mathrm{C} \)
となります。図2から、もとの温度が\(10\,{}^\circ\mathrm{C}\)であることがわかるので、10分加熱後の温度は
\(10\,{}^\circ\mathrm{C} + 50\,{}^\circ\mathrm{C} = 60\,{}^\circ\mathrm{C}\)
と求めることができます。
最後に
本記事では、「カロリー計算」について解説しました! 「熱の移動と温度変化」はそもそも出題頻度は少ない分野ですが、その中ではよく見かけるのがカロリー計算の問題です。カロリーと熱量、エネルギーがそれぞれ何か曖昧だった人も、すべて同じものを指しているということが理解できたでしょうか? また。カロリー計算の基本的な知識と解き方について、ヒント無しに答えることができるようになったでしょうか? カロリー計算は比較的似たような出題が多く、パターン化して問題に取り組めるため、これらの基本的な問題を押さえておけば、受験対策としてはかなりいい線を行っていると思います。まだまだ理解が追い付いていないという人や、混乱が生じている人は、今回紹介したような基礎的な知識と練習問題を使って、頭の中を整理していきましょう! それでは引き続き中学受験理科の勉強を頑張ってください!
おすすめ記事
- 熱の移動と温度変化 ~「熱」とは何かを理解し、問題を解きながら基礎を知ろう!~【中学受験理科】
- 浮力が苦手な人必見!点数をとる方法は?
- てこのつり合いのまとめ その1
- てこのつり合いのまとめ その2
- 物理の勉強法~苦手な人への処方箋
- 【中学受験】今だからできる!理科勉強法・克服法 物理編