今回の記事では方陣算について取り扱う記事の発展編として,三角形・多角形の方陣の特徴を解説していきます。基本的な考え方は前回の基本編でご紹介したものと変わりませんが,実際に難関中学校の受験で登場されやすいのは四角形以外の方陣算です。そのため重点的に対策しておく必要があります。合格のために一読いただけますと幸いです。
基礎編の振り返り!
それではまず前回の記事でご紹介した内容を振り返っていきましょう。そもそも方陣算とは石やおはじきなどを特定の形に合わせて並べていくときの文章題を指しました。このときの配置によって問題の中身がいくつかに分類できるのですが,その中でも基礎編では四角形の方陣,とくに中身の詰まった中実方陣・中身の抜かれた中空方陣の性質についてご紹介していきました。
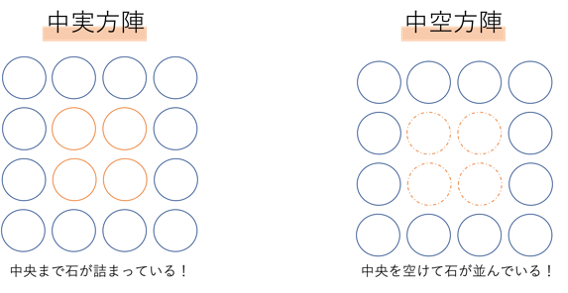
そしてそれぞれの図形において全体の石の数・外周の石の数・一辺の石の数,中空方陣の場合は列の数の関係を整理していきましたね。初めに中実方陣ですが,中実方陣では次の3つの関係の式をご紹介しました。
全体の石の数=たての辺の数×よこの辺の数
外周の石の数= (1辺に置かれている石の数×4)-4
また中空方陣で覚えておきたい3つの式もご紹介しましたね。
全体の数=隅の数×4+たての部分×2+よこの部分×2
たての部分=たての辺の数-(たての列の数×2)
よこの部分=よこの辺の数-(よこの列の数×2)
外周の石の数= (1辺に置かれている石の数×4)-4
これらの関係は実際のところ図形をプリントに書きこんで数え上げていけば別段覚える必要はないですが,毎回数えていくのは手間ですし何より時間がかかってしまいます。そのため計算の簡略化のためにも,しっかりと覚えておきましょう。なお今回の三角形・五角形の方陣算でも,四角形の方陣算と同じ考え方で性質を捉えていきます。そのため基礎編でご紹介した分割・切断などのテクニックを忘れてしまった場合にはぜひ基礎編の記事を参考にしてみてください。
三角形の方陣算!
それではここからは多角形の方陣算の性質を眺めていきましょう。今回ご紹介するのは多角形のうち,方陣算で登場されやすい三角形と五角形の方陣です。まずは三角形の法人について考えていきましょう。この三角形の方陣はピラミッド算と呼ばれることもあります。石が並べられた形がピラミッドに似ていることからこのような名前で呼ばれるのですが,配置されている石の外周の数や全体の数が問われることから方陣算の一つとして扱われます。そしてこのピラミッド算では,組み上げた段数と1辺に置かれる石の数が等しくなることが大きな特徴として挙げられます。この組み上げた段数=1辺に置かれる石の数によって,三角形は1段ピラミッド,2段ピラミッド,……と呼ばれていきます。
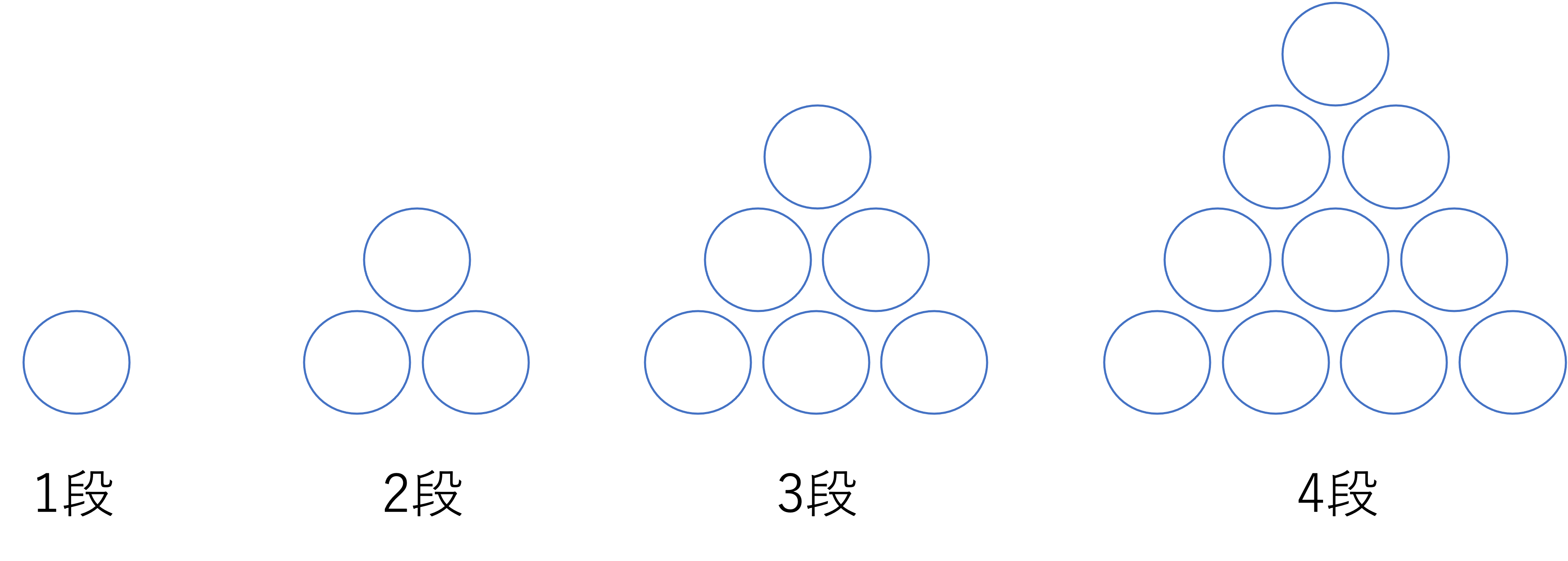
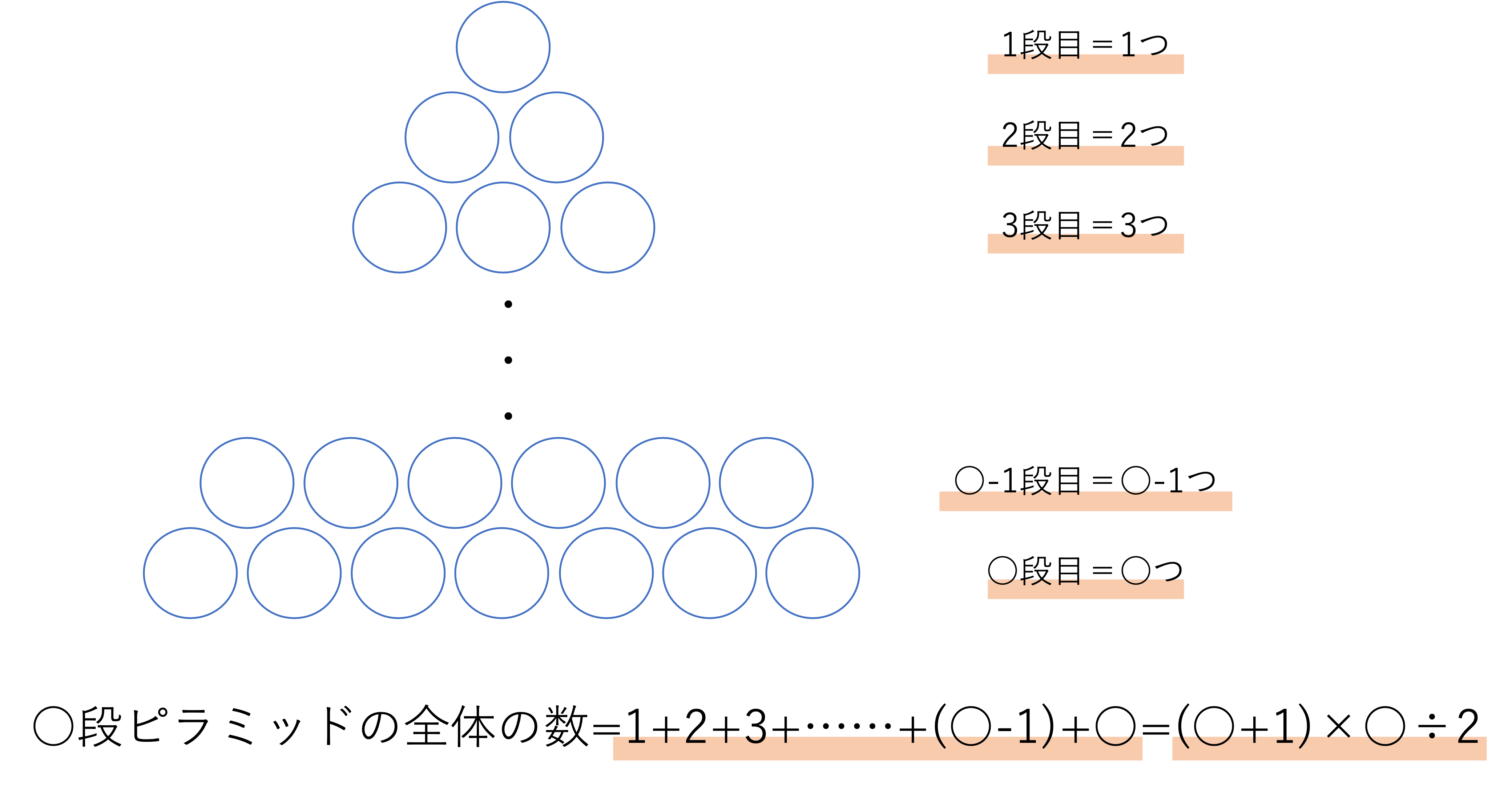
そしてこの段の数が変わるともちろん全体の数も変わってきますね。そこでまずは段の数と全体の数の関係を見ていきましょう。いま1段のときのピラミッドを見ると全体の数は1つですが,これが2段になると1段目の1つと2段目の2つを足して3つになります。そして今度は3段目を見ると,こちらは1段目に1つ・2段目に2つ・3段目に3つで合計6つになっていることがわかります。この関係から○段ピラミッドを作る石の数の合計は,1から○までの全ての数を足した値になることが分かります。これを式に表すと次のようになります。
○段ピラミッドの全体の数=1+2+3+……+(○-1)+○
そのため全体の数を問われたらこの式を使って解いてみましょう。ただこのような足し算は○の中身が小さいときは簡単にできますが,中身が大きいときはそうもいきません。加えて,例えば「全体の数が240個のときの段の数」といったような全体の数が与えられている場合は上手く計算できないという問題もあります。そこで全体の数は次の式でも数えられるということを覚えておきましょう。式の導かれ方は高校の数学などで習う難しいものなので今回は省略しますが,式の形は覚えておくと役に立つでしょう。
○段ピラミッドの全体の数=(○+1)×○÷2
次は外周の数を考えていきましょう。外周の数とは図形の一番外側に存在する石の数です。例えば上の図の4段ピラミッドだと中央以外の全ての石が外側に存在することになります。これを数えると9個だと分かるので,外周の数は9個なるわけです。このように図を書いて考えることができる問題では外周の数は数え上げるだけで答えることができますが,問題は図が書けないくらい段の中身が大きくなっていったときのことです。
このような場合,1辺の数を純粋に3倍してしまうといったような間違いをしてしまうことがあります。しかしこれでは計算は正しくできません。先ほどの4段ピラミッドの外周は9個でしたが,これも3倍しているわけではありませんよね。そのためここで計算の式を覚えてしまいましょう。
このときの関係の考え方を端的に述べてしまうと,大きなピラミッドの中に小さなピラミッドを見つけることで答えを計算することができます。例えば先ほどの4段ピラミッドでは,外周の中に1段のピラミッドが存在するようにみなすことができますよね。そのため4段ピラミッドの全体の数から1段ピラミッドの全体の数を引く,つまり10-1=9個と計算できるのです。これは次のような5段ピラミッドでも同じです。
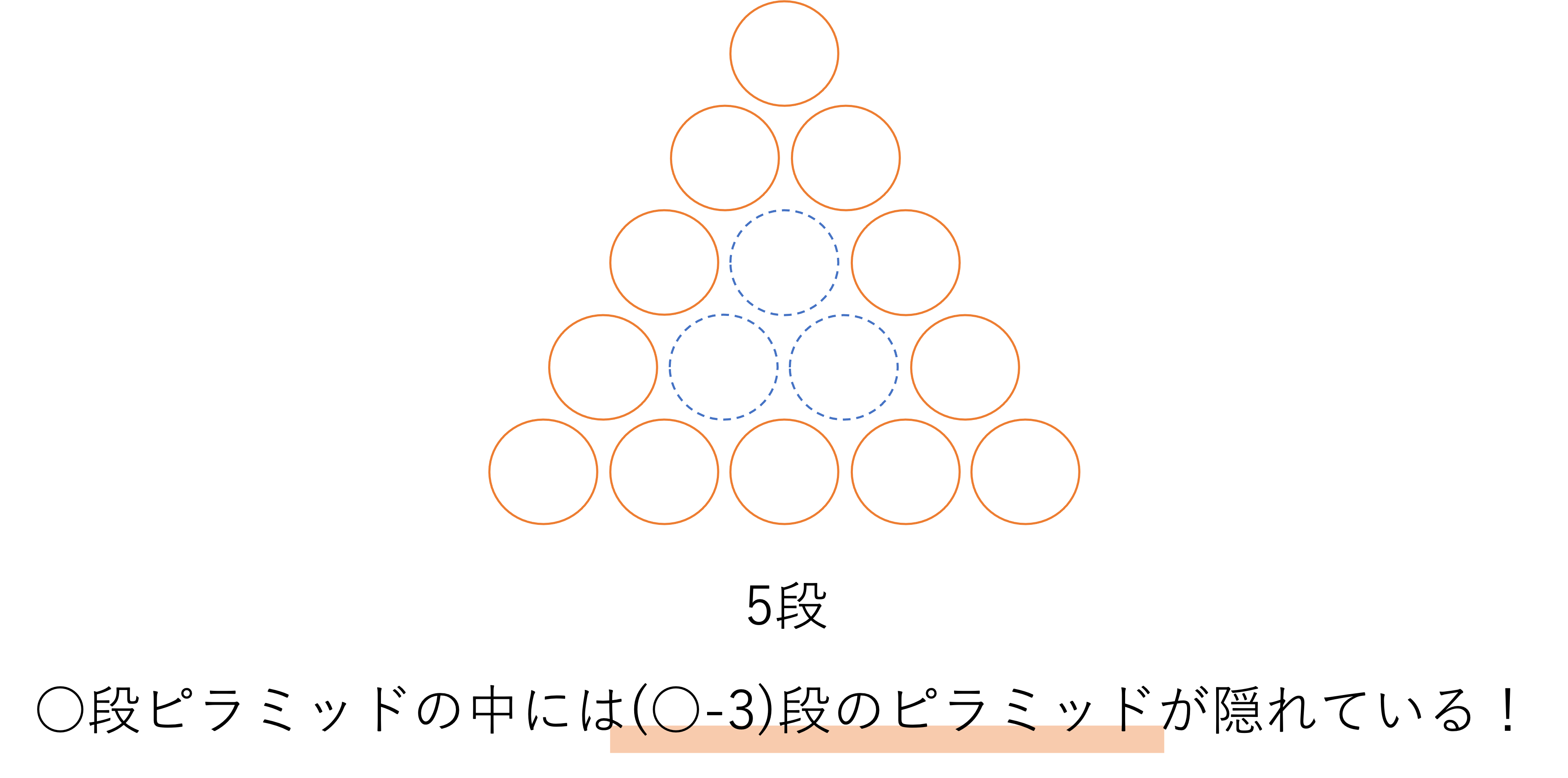
そしてこのように4段の中に1段,5段の中に2段,……と考えていくと,○段の中には(○-3)段のピラミッドが存在していると考えられますね。このことから外周の数は次のように定義することができます。「図を書かないと探しづらい,でも図を書くには面倒」という厄介な問題なので,この機会に計算式を頭に入れてしまいましょう。
○段ピラミッドの外周の数=○段ピラミッドの全体の数-(○-3段ピラミッドの全体の数)
○段ピラミッドの外周の数= {(○+1)×○÷2}-{(○-2)×(○-3)÷2}
五角形の方陣算!
続いてご紹介するのが五角形の方陣算です。前述したように方陣算では三角形以外だと五角形が頻出の問題です。そして三角形・四角形・五角形の式が分かれば,あとはその応用の考えで他の図形の問題も解くことができるようになります。そのような理由から,本章では五角形を扱いながら,同じように全体の数・外周の数・1辺の数の関係を確認していきましょう。
まず全体の数ですが,その前に五角形の方陣算の全体像をわかりやすくするために,三角形の場合と同様に1辺の数が1個のとき,2個のとき,……と数字を増やしながら五角形の方陣を作っていきましょう。図のようなイメージが登場したら,ここからご紹介する公式や関係が使えると思っていただければ幸いです。
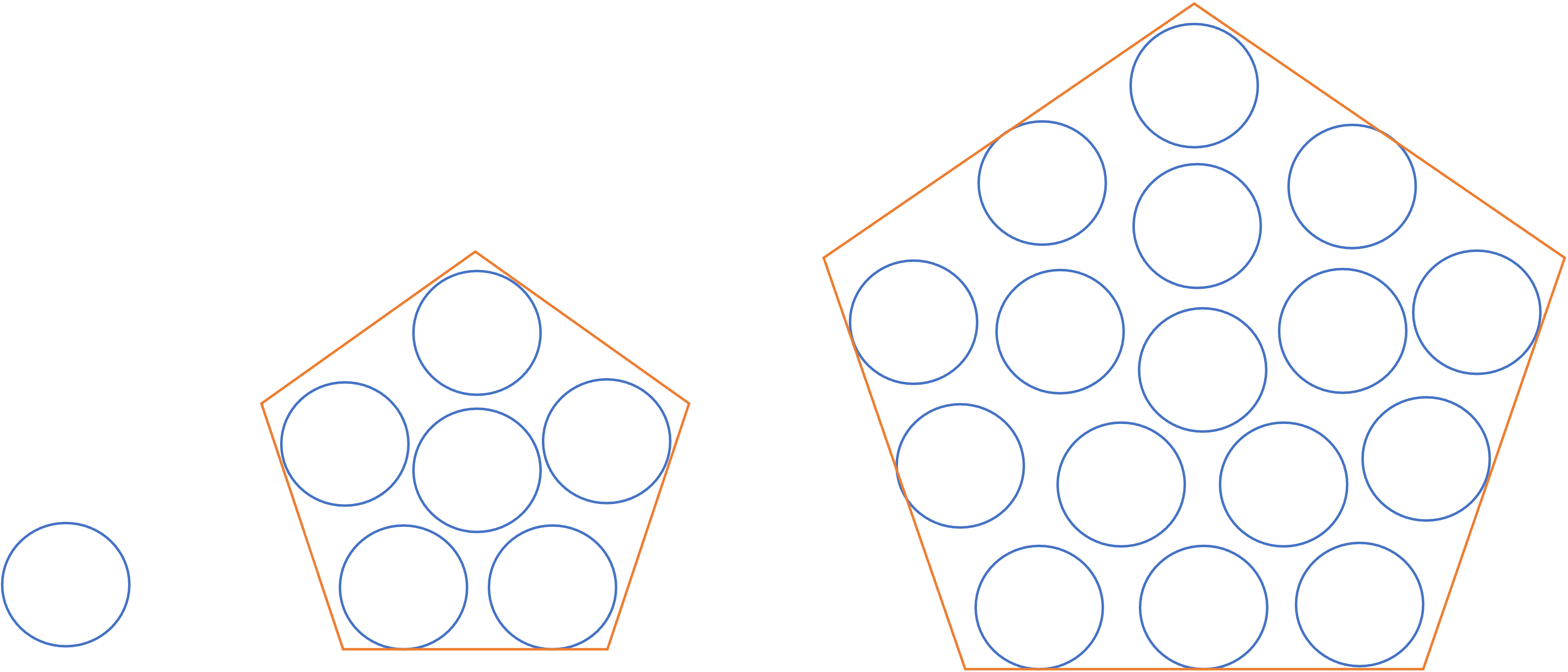
さて,まずは全体の数の計算方法からご紹介していきます。中実方陣のときは面積の求め方を応用させて個数の数え方を説明しましたが,五角形の面積の公式が存在しない以上,工夫して計算することが必要となってきます。そのため一筋縄ではいかないのですが,ここで重要になるのが分割というテクニックです。五角形の方陣はその中身を見ると,中心+いくつかのピラミッドで構成されていることが分かります。例えば上の図の3段ピラミッドだったら,中心と2段のピラミッドが5つに分割することができますね。そしてこの五角形において1辺に対して3個の石が並べられていたことを考えると,1辺に○個の石が並べられている五角形の中には(○-1)段のピラミッドが5個隠れているとみなせます。この関係は五角形の一辺が5個でも6個でもそれ以上でも成り立ちます。是非覚えておくといいでしょう。

そしてこの切断の関係から,1辺が○個の五角形の全体の数を計算するには,(○-1)段のピラミッドの全体の数を5倍して中心の1個を足せばいいということが分かります。以上のことから,関係は次の式に整理できます。
1辺が○個の五角形の全体の数=5×(○-1)段のピラミッドの全体の数+1
1辺が○個の五角形の全体の数=5×○×(○-1)÷2+1
やや計算式が複雑ですが,ピラミッドのところで登場した式をまずは完璧に覚え,その応用として理解していくといいでしょう。そして最後に外周の数ですが,こちらも三角形の方陣算の外周の数のところでご紹介したのと同じ考え方,つまり図形の中に隠れている小さな図形への注目が有効です。例として,先ほどから使用している1辺が3個の五角形を使って説明していきましょう。この中には1辺が2個の五角形を見つけることができます。このことから外周の数は元の五角形の全体の数から内側に隠れている五角形の全体の数を引くことで計算できるということができます。
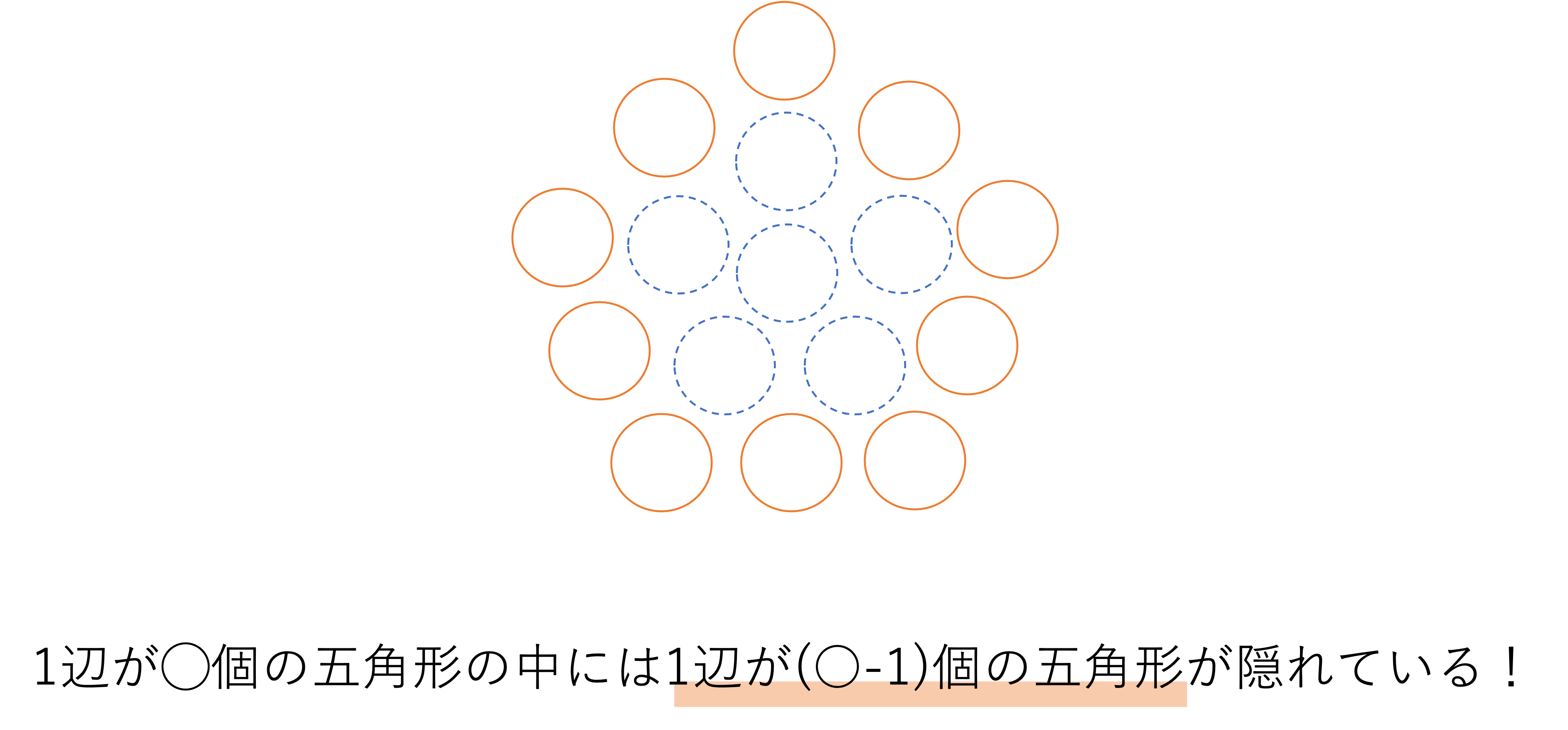
そしてこれを一般化すると,1辺が○個の五角形の外周の数は,その全体の数から1辺が(○-1)個の五角形の全体の数を引くことで求められると言えますね。算数っぽく式に表すと次のようになります,頭の片隅に入れておきましょう。
1辺が○個の五角形の外周の数=全体の数-1辺が(○-1)個の五角形の全体の数
1辺が○個の五角形の外周の数={5×○×(○-1)÷2+1)-{5×(○-1)×(○-2)÷2+1}
しかし,この式だとまだなかなか覚えづらいですね。そこで計算式を変形させて,より簡単な形で覚えてしまいましょう。外周の数は次のように整理することができます。
1辺が○個の五角形の外周の数=(○-1)×5
この式はつまるところ,外周を辺の数から1引いた個数が5個集まったまとまりと捉えていることを指します。例えば1辺が3個の五角形であれば。その外周は2個×5つとみなすことができますよね。そのため隠れている図形を見つける作業は必要ないのですが,この考え方を知っていると三角形・五角形以外の図形が登場したときに便利なので今回ご紹介しました。よろしければセットで覚えてもらえると幸いです。
終わりに
今回の記事ではこれまで三角形・五角形の方陣算の性質をご紹介してきました。先ほども述べましたが,難関校ではこのように若干取り組みづらい方陣が問題として出題されることが多いです。そのため前回の記事でご紹介した中実方陣・中空方陣はもちろんのこと,今回ご紹介した図形の特徴も覚えておきましょう。次回の発展編では受験問題を引用しながら実践的な攻略法をご紹介していきますので,そちらもよければご参照ください。本記事が今後の学習のお役に立てば幸いです。