もうすぐ新学期ですね。来年中学入試を志されている方はもちろんのこと,これを機に勉強に励んでいこうとするご家庭も多いかと思われます。
本記事ではここ数年で行われた中学入試の問題の傾向を分析していくものになります。【チャレンジ校編】,【難関校編】,【有名校編】に続いて今回は,偏差値で言うと50以下の進学校で出された算数の問題に焦点を当てていきます。このレベル帯の学校は滑り止めとして受験されるお子様も多いかと思われます。よろしければ参考にしてみてください。
Contents
1つ目の出題傾向:計算の決まりのおさらい問題
まず初めに確認できた傾向は,計算の決まりと言う分野からの出題です。算数には,問題を解くときにどこから解けばいいのかという順番が存在します。進学校ではこのような基礎的な問題も出題されています。例えば次のような問題が登場していました。
次の□にあてはまる数を求めなさい。
\(28-{28-4\div(8-2)\times9}\div11=□\)
(名古屋中学校(2020),一部改題)
次の□にあてはまる数を求めなさい。
\(9+(8+2\times8\div4)\div3\times4=□\)
(埼玉栄中学校(2020),一部改題)
一見簡単なようにも思えますが,実際の受験になるとこのような問題でも緊張して解けなくなってしまうことが多々あります。また計算の決まりからの問題は,分数や少数などと絡めて難しくすることもできますので,近年簡単な問題が多いから解いて油断することはできません。そのためきちんと対策することが必要になります。
決まりが問われる計算問題の対策法は?
では計算の決まりが問われたときに備え,どのような対策をとっておけないいのでしょうか。ここからは勉強する上で押さえておくポイントをご紹介します。
まず大事なことが,正確に決まりを抑えることです。かっこの中→かける・わる→たす・ひくの順番をきちんと覚え無ければ,解ける問題も解けません。進学校受験では,基礎をしっかり身につけておくことが重要です。
その次に,いくつもの問題を繰り返し解いて,計算のルールに慣れていく必要があります。きまりを知っているのと,実際に問題の中で思い出し活用できるのとは訳が違います。最初のうちは間違えることもあるかもしれませんが,量を積めば正答率が上がっていくと思います。また問題を解くと言うのは,四則演算に限らなくても大丈夫です。どんな問題でも計算は絶対に必要になるため,日頃から算数に触れることで計算力を上げていきましょう。
これよりレベルの高い受験校では,計算を簡単に解くための工夫なども覚える必要がありますが,まずは基礎力をしっかり自分のものにしていく意識を持って勉強していけば問題ありません。
2つ目の出題傾向:資料の調べ方に関する問題
2つ目の進学校における出題傾向は,資料の調べ方からの出題です。この範囲はグラフの読み取り能力や,平均値・中央値などの代表値を求める能力が問われます。例えば次の2つのような問題が登場していました。
下の表1は,あるクラス16人の算数のテストの点数です。次の問いに答えなさい。
63,15,44,77,47,20,84,80,62,70,61,37,96,50
(1)クラス16人の算数のテストの平均点を求めなさい。
(2)上の表1を下の表2に整理したときに(ア),(イ)に入る数字を求めなさい。
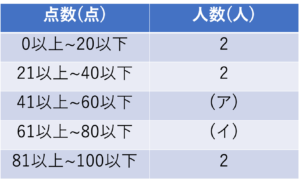
(3)算数のテストで平均点以下の点数を取って人数は,全体の何%か求めなさい。
(武南中学校(2020),一部改題)
ある学校の生徒に居住地についてアンケートをしたところ,26%が埼玉県以外の生徒でした。その内訳を見ると,東京都が最も多く35%でした。次の各問に答えなさい。
(1)問題文の内容に適した円グラフを下の図1~図4から選びなさい。
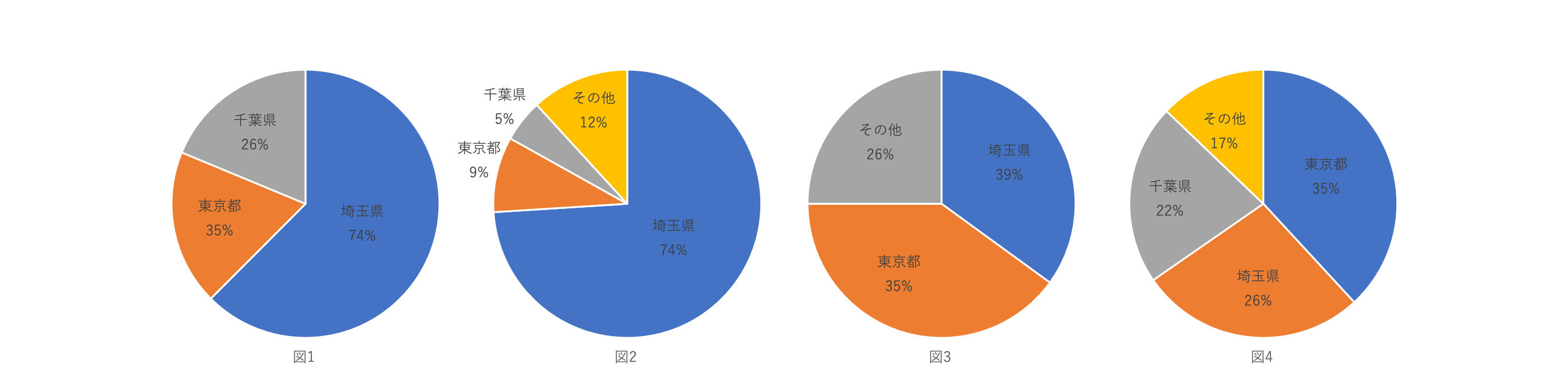
(2)東京都の生徒が182人のとき,全校生徒の人数を求めなさい。
(獨協埼玉中学校(2020),一部改題)
このようなグラフに関連する問題は,あまり応用の余地がないため難関校では出題されにくく,進学校ならではの出題傾向だと言えるでしょう。そのため受験にあたって重点的に対策する必要があるといえます。
資料問題への対策法は?
では資料が関連した問題について,どのように慣れていけば良いのでしょうか。その攻略法の一つが,グラフや表の見方をしっかりと身につけることにあります。
中学受験で登場するグラフは,棒グラフ・円グラフ,折れ線グラフに帯グラフといったところでしょうか。表にも,よく見るタイプのものに加えて度数分布表なども稀に登場します。これらのグラフは他の頭を使う計算とは違い,知らないとどうやっても読み取れないものです。そのため参考書などを使って知識として定着させる必要があります。
そして定着させた知識を使って実際にグラフを眺めてみるトレーニングも必要です。これについては,算数の問題に取り組むだけでなく,新聞やニュースを保護者の皆様と一緒に読むことも有効かと思われます。むしろ身の回りにある図表から慣れていった方が,お子様にとってスムーズに学力向上を図れるかもしれません。「算数の力を伸ばすために算数ばかり勉強する」必要はありません。柔軟に楽しく勉強していきましょう。
3つ目の出題傾向:角度を求める平面図形の問題
最後にご紹介するのは,角度を求める問題という特徴です。平面図形からの出題は,どのレベルの学校でも,そしてどの年度でも出題されがちです。そのため読者の皆様も対策しなければ,と考えているのではないでしょうか。例えば下のような問題が出題されていました。
右の印をつけた角の大きさの合計を求めなさい。

(名古屋中学校(2020),一部改題)
下の図の正九角形において,角xの大きさを求めなさい。
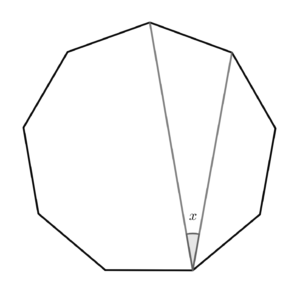
(立正大学付属立正中学校(2020),一部改題)
どれも標準的な平面図形の問題です。同じような問題を見たことある人も多いのではないでしょか。しかし,もちろん本番当日には見たことがない問題が出てくるでしょう。どんな問題が出てきても対応するために,勉強法や攻略の糸口を知っておかなければなりません。
平面図形への対策法は?
ではこのような平面図形,とりわけ角度の問題に対処するために,どのように勉強していけば良いのでしょうか。以下ではその攻略法についてご紹介いたします。
まず大事なのが,具体的な知識や公式ではなく,視点を変えて図形を眺めるための能力を伸ばすことです。平面図形の問題に関しては,見たこともない問題が次々に出てくるので,どんな図形が登場しても適応する実力が必要です。
この適応力を養うためには,いくつもの問題を解いていくというより,じっくりと時間をかけて一つの問題を解く演習が効果的でしょう。隠れた図形や補助線の弾き方はすぐ身につくものではなく,試行錯誤を繰り返していくことで初めて自分のものになります。
したがって簡単な問題や慣れている問題をいくつも解いたところで大きな意味はなく,頭を悩ませながら答えにたどり着くという経験が意味を持ちます。初めのうちは集中力がもたないかもしれません。そのような場合には休憩を挟みながら,また保護者の方がヒントを出しながら取り組むよう促すといいでしょう。
この試行錯誤の訓練は,やがては試験時間中ずっと継続する集中力を養うことにつながります。その意味でも時間をかけて演習に取り組むことは大切でしょう。是非参考にしてみてください。
まとめ
今回は進学校で出題されがちな算数の問題の傾向と,どのように対策していけばいいのかをご紹介していきました。改めて今回確認できた傾向・対策をまとめておきましょう。
- 計算の決まりという傾向→決まりを覚え,算数に継続的に触れることで対策!
- 資料の調べ方という傾向→読み取り方を学び,身の回りの図表に触れることで対策!
- 角度の計算という傾向→時間をかけて試行錯誤しながら演習することで対策!
今年進学校を受験される方は是非とも上の対策法に取り組んで,合格に向けて効率よく勉強していただけたらと思います。本記事が合格の手助けになれば幸いです。よろしければ下にご紹介する記事やテキストを活用しながら,更なる学力向上を図っていきましょう。
(ライター:大舘)
















