今回は比例と反比例について取り上げるシリーズの2回目として,グラフの書き方や読み取り方をご紹介していきたいと思います。比例と反比例の基本的な考え方については,今回の冒頭でもさらっと振り返るつもりですが,いまいち思い出せない人は前回の記事をご確認ください。比例・反比例に代表される比についての単元は中学受験でほぼ必須と言っていい知識です。早めのうちにマスターできるよう,頑張っていきましょう。
Contents
初級編のおさらい!
まずは初級編で習ったことを軽くご紹介しましょう。前回の記事とは,どんな関係を比例あるいは反比例と呼ぶのか・どのような見分け方があるのか,といったことに焦点を当てて解説していきましたね。鉛筆の問題やアメの問題を思い出しながらお読みいただけますと幸いです。
比例とは?
まず比例について復習していきましょう。そもそも比例・反比例とは2つの異なる数の間に存在する法則性のことを指します。その中でも比例と言われたら,ある数が2倍,3倍,4倍,…と増えていくと,それに伴ってもう片方の数も2倍,3倍,4倍,…と増えていく関係のことを指します。代表的なものが,ものの個数と値段の関係ですね。1個100円のものを2倍買うと値段も2倍に,3倍買うと値段も3倍に,4倍買うと値段も4倍に…と増えていきます。そのため比例と呼べるわけです。
比例の関係を見極める上で重要な要素が,数が増えていっても変わらない1つあたりの基準の有無を考えることです。例えば先程の個数と値段の例で言うならば,個数がどれほど増えようと・値段がどれだけ増えようと1個〇〇円という基本の数は変わりませんよね。このように1個・1cm・1回などの単位あたりの量が存在している場合には比例の関係が導き出せる可能性が多いです。参考にしてみてください。
反比例とは?
続いて反比例について復習していきましょう。反比例とは,ある数が2倍,3倍,4倍,…と増えていくと,それと反対にもう片方の数が2分の1,3分の1,4分の1,…と減っていく関係のことを指します。こちらは,ある数のものを分けるときの個数と人数の関係に代表されます。決まった量しかないものを分けるとき,2人で分ければ2等分,3人で分ければ3等分,4人で分ければ4等分になります。このような関係を人数と個数とで別々にみていったとき,どちらかが×2,×3,×4,…となれば,他方の数が÷2,÷3,÷4,…となります。それゆえ反比例の関係と言えるわけです。
反比例の関係を見極める上で重要なことが,問題文中で一定に設定されている量が有るか無いかを考えることです。例えば先程の個数と人数の例で言うならば,人数がどれほど増えようと・1人当たりの個数がどれだけ増えようと全体で〇〇個という一定の量は変わりません。このような変わらない数を基に考えると反比例を見つけやすくなります。覚えておきましょう。
比例のグラフの書き方
それでは本題のグラフの書き方を学習していきましょう。前回までで確認した,式の立て方や表の作り方を思い出しながら考えていきたいところです。一つ一つ手順を確認していきますが,万が一既に知っている方がいれば,読み飛ばしていただいても問題ありません。
まず重要なことが,2つの関係が比例しているかどうかの確認です。そして比例していることがわかったら,次に表を書いていきます。この辺りの作業は前回取り扱ったところなので省略します。もし思い出せない方がいましたら初級編の記事をご確認ください。ここでどれだけ表を書けばいいのか,と疑問に思うでしょうが,目安としては縦軸あるいは横軸の限界まで書くことをオススメします。
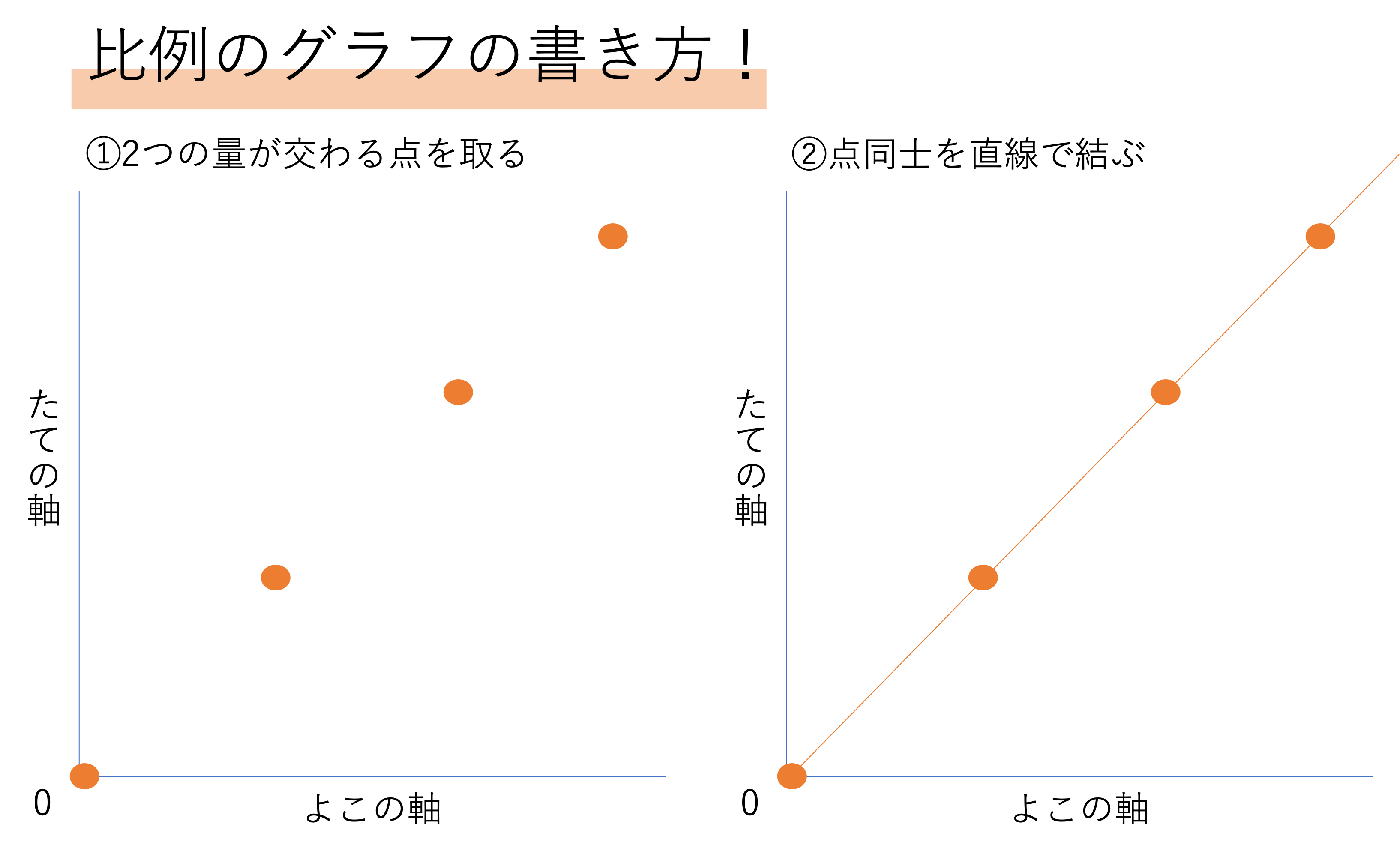
さて,表に2つの数字の関係を表せたら,次にやることは2つの量が交わる点を打つことです。たての軸のラインと横の軸のラインが交差するところを探して座標を書き込みます。例えば1個120円という2つの量の関係があったとするならば,個数の「1」というラインと値段の「120」というラインを辿り,ぶつかっているところに印をつければいいですね。ちなみにこのとき0の点を打つことを忘れないようにしましょう。0の点を打つ理由は簡単で,例えば値段と個数の例を使うのであれば0個のとき0円になるからですね。意外と忘れやすいところなので注意しておきましょう。
そして点をグラフに打ち込んだら,すべての点を通るように定規で押さえて直線を引けば完成です。ちなみにこのとき,直線は0から一番遠い点で切れるのではなく,0から一番遠い点を突き抜けるようにしましょう。それは,比例という関係が点の先でも続いていくからですね。もちろんグラフ用紙からはみ出るほど書く必要はありませんが,用紙いっぱいまで書き切ることを忘れないでください。
実際にグラフを作ってみよう!
ここからは例題を引用しながら実際に比例のグラフを作っていきましょう。使用する例題は基礎編でも出した鉛筆の値段に関するものです。前回分のメモやノートがある人はそれを持ち出してきてもいいかもしれません。
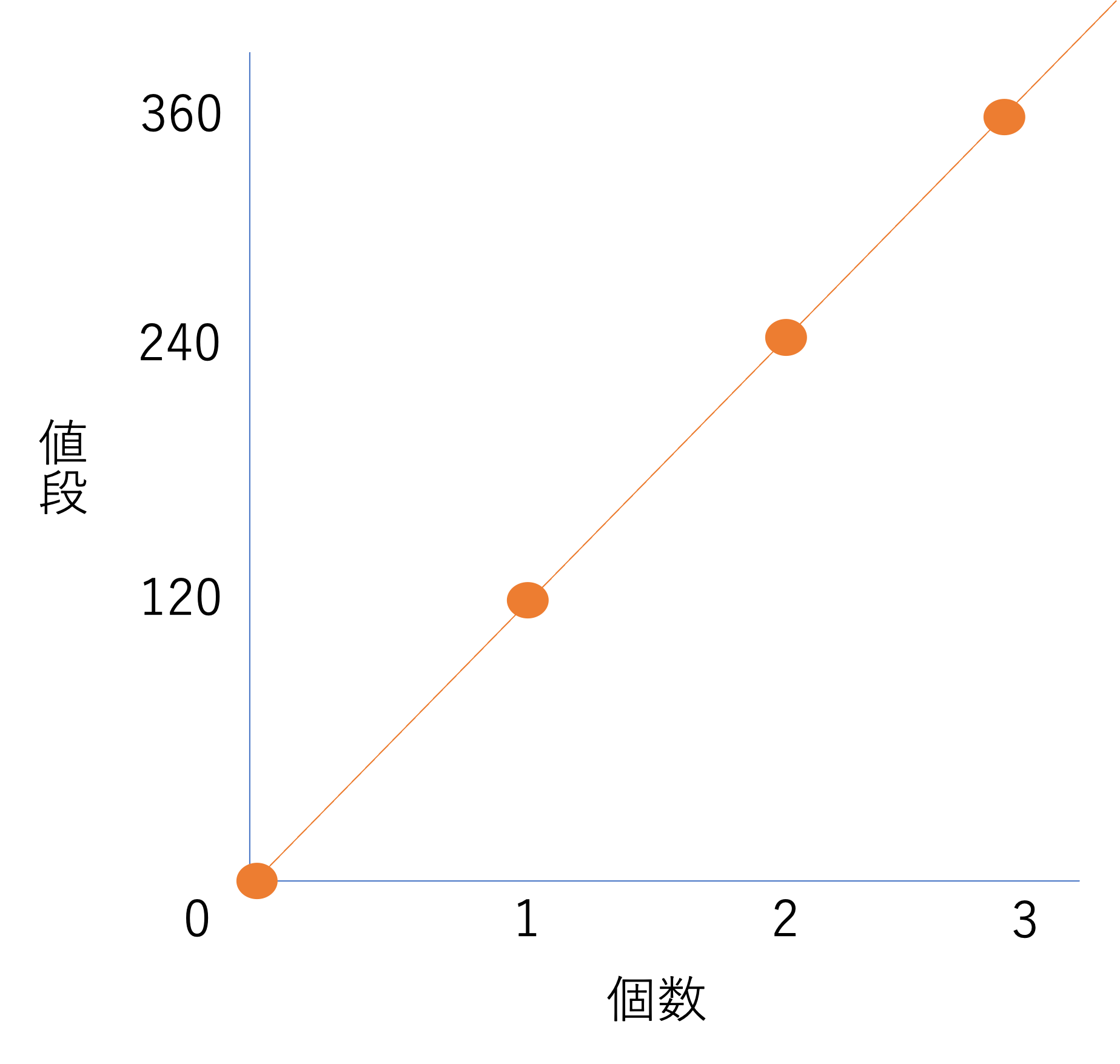
ここに1個120円で売られている鉛筆があり,それを何本か購入することにします。鉛筆の個数と値段の関係をグラフに表してください。
ではさっそくグラフの作成に移りましょう。まずは値段と個数が比例していることを確認するところから始めていきましょう。1本買うと120円,2本買うと240円,3本買うと360円,……という風に関係を眺めていくと,片方が2倍,3倍,…になるとそれに伴ってもう片方も2倍,3倍,…になることが分かります。そのため2つの数の関係は比例といえますね。そして今回は省略しますが,この関係から表を作成することもできます。ちなみに表は必ず必要なものではありません。慣れてきたらグラフに直接点を打ち込んでいってもいいでしょう。
そして個数と値段の関係を点でグラフに書き込み,その点を直線で結んでいけば完成です。おそらくここまで進めてきて,あまり難しくないように感じた人もいるかもしれません。実はグラフの作成というのは手順がやや多い・初めてだとわかりづらいだけで慣れてしまえばスラスラと解けるのです。そのため早め早めから完璧にして,余裕を持って受験に臨みたいですね。
ちなみにグラフを書く上での2つの注意点,0を通ることと最後の点から突き出ていることはお忘れないでしょうか。細かいところですが,忘れていた人はぜひ修正しておきましょう。回答例は次のようになります。このグラフは最低レベルの3個360円までしか点を取りませんでしたが,これより多くても問題はありません。
反比例のグラフの書き方
それではここからは反比例のグラフの書き方を学んでいきましょう。この章でも,前回までで確認した,反比例の式や表を思い出しながら考えていきたいところです。こちらも既にバッチリ理解できている人は読み飛ばしてしまって構いません。
はじめに大事ことが,やはり2つの関係が反比例しているかどうかの確認です。そして比例していることがわかったら,次に表を書いていきます。この辺りの作業は前回取り扱ったところなので,再確認したい方は初級編の記事をご覧ください。ここでも表のサイズは,縦軸あるいは横軸の限界を目安に書くことをオススメします。
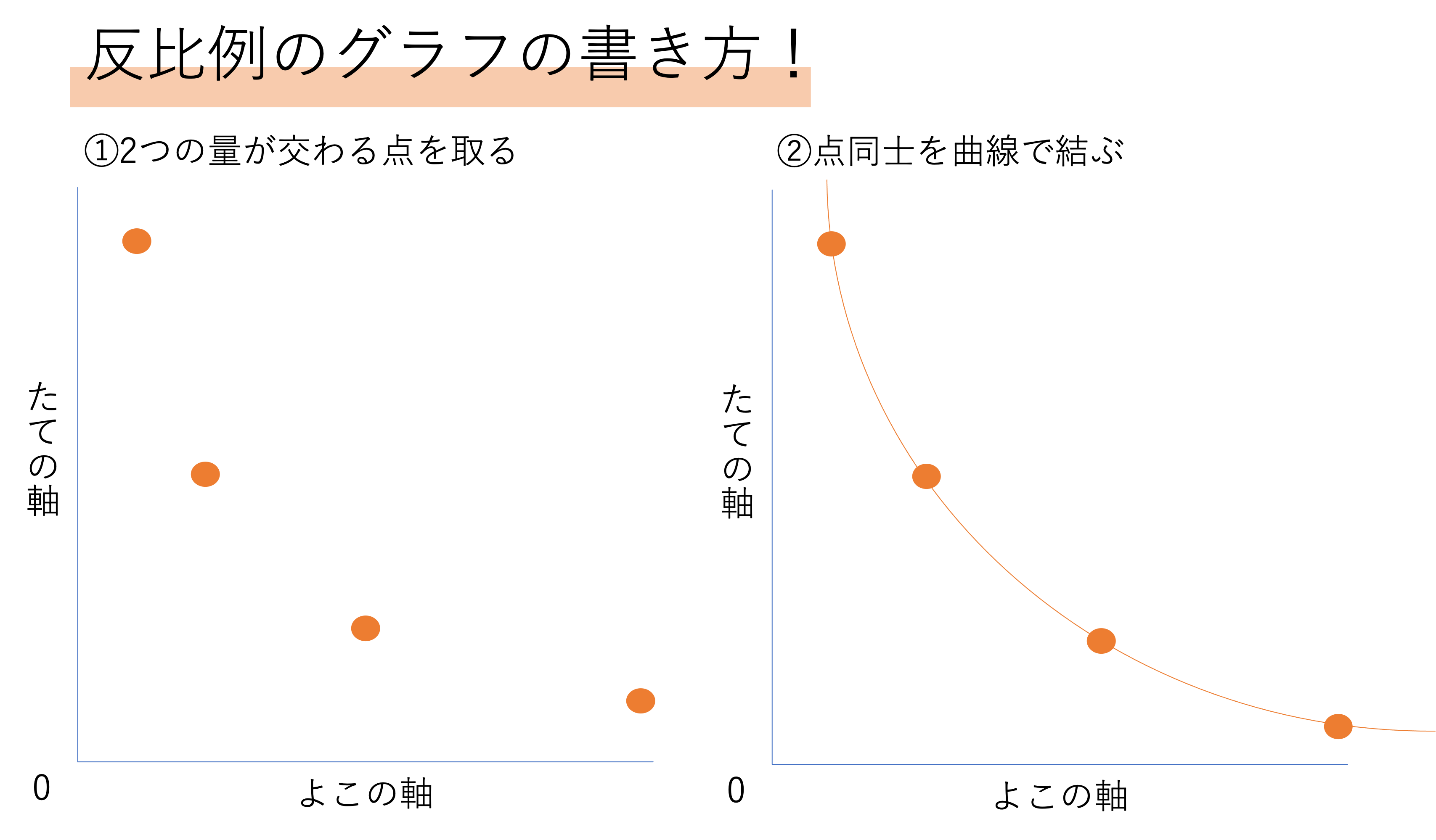
そして,表に反比例する2つの数の関係を表せたら,次にやることは2つの量が交わる点を打つことです。たての軸のラインと横の軸のラインが交差するところを探して座標を書き込みます。例えば1人5個ずつで12人に配る,という関係があったとするならば,個数の「5」というラインと人数の「12」というラインを辿り,交わる箇所に点をつければいいですね。この辺りまでは比例とやることはさして変わらないですが,大きく違うことがたての軸も横の軸も0を通らないということです。これは例えばモノを配るという場面を想定するならば,0人で分けることも0個で分けることもできないからですね。
そして点をグラフに打ち込んだら,すべての点を通るように曲線を引けば完成です。比例では直線でしたが,ここでは曲線を書くという違いがあります。コンパスなどを使う必要はありませんが,綺麗な右下がりのカーブを描くように頑張りましょう。
ちなみにこのとき,曲線は0から一番遠い点を突き抜けるようにして用紙いっぱいまで書き切るようにしましょう。その理由は比例での欄で挙げたものと同じです。そしてもう1点気をつけて欲しいことが,絶対にたての軸とも横の軸ともぶつからないようにすると言うことです。上で説明したように,反比例ではたてが0になることも横が0になることもあり得ません。減点の対象になるかも知れませんので,日頃から気をつけておきましょう。
実際にグラフを作ってみよう!
それでは反比例のグラフも実際に作ってみることにしましょう。ここで使う例題も前回の初級編で使ったものですので,過去の記事を一緒に見ながら解いてみるとわかり亜y水かも知れません。
ここに30個のアメがあり,それを□人で分けることにします。このときに1人あたりに配られるアメの数を□を使って表してください。
それではグラフの作成にとりかかりましょう。まずは人数と個数が反比例していることを確認するところから始めていきましょう。1人で分ける30個,2人で分けると15個,3人で分ける10個,……と関係を追っていくと,片方が2倍,3倍,…になるともう片方の数が2分の1,3分の1,…になることが分かります。そのため2つの数の関係は反比例といえますね。そしてこの関係から表を作成することができたら,あとは人数と個数の関係を点でグラフに書き込み,その点を曲線できれいに結んでいけば完成です。ちなみに先程の比例も今回の反比例も,どちらの数がたてでどちらの数が横かなどはそこまで気にしなくても問題ありません。
ちなみにグラフを書く上での2つの注意点,0を通らずたての軸や横の軸と交わらないことと最後の点から突き出ていることはお忘れないでしょうか。細かいところですが,忘れていた人はぜひ修正しておきましょう。回答例は次のようになります。このグラフは最低レベルの5人6個までしか点を取りませんでしたが,これより多くても問題はありません。
グラフを読み取る上で大切なこと!
これまではグラフの「書き」に注目してきましたが,最後にグラフの「読み」に焦点を当てて少しお話ししていきましょう。比例・反比例のグラフを正しく理解して読み取り問題で生かすために重要なことは,グラフの形から関係を予測することです。
比例のグラフは直線で,反比例のグラフは曲線で描けると上でご説明しましたが,これは逆のことも成立します。つまり右上がりの直線のグラフは比例,右下がりの曲線のグラフは反比例の関係を指している,ということです。このことから形と関係をある程度結びつけて考えることが可能になります。当然と言われれば当然のことですが,初めのうちは意識して覚えるといいでしょう。
また予測について,比例か反比例かを見分けた後も,グラフの形か関係の式を予測することも可能です。グラフを書く流れを紹介するときに点を打ちましょうと言いましたが,読み取り問題でも同じようにグラフ中に点が書き込まれていることがほとんどです。そしてこの点をいくつかリストアップすれば,照らし合わせることで比例あるいは反比例の表を作れますよね。表が分かれば式も立てられる,ということでグラフから式を導くことも可能です。
このようにグラフを見れば,そして書くときの手順と逆の作業で考えていけば,いろいろなことがわかります。予測がある程度導けたらそこから問題を簡単に解くヒントを得られる可能性が生まれますので,ぜひ予測するというテクニックは身につけておきたいところです。
まとめ
今回の記事では比例と反比例について解説していくシリーズの第2回中級編としてグラフの書き方や読み取り方についてご紹介していきました。受験において「グラフを書きなさい」という問題が出題される事は滅多にないですが,読み取り問題はおそらくどこの学校でもどの年度でも登場していることでしょう。そのため本記事だけでなく,参考書籍やおすすめ記事なども適宜使いながら更なる知識定着を狙っていきましょう。本記事が今後の学習のお役に立てば幸いです。

















