今回の記事では水の深さと体積について扱っていきます。この単元はそこまで難しいものとしては取り扱われませんが,中学入試ではたくさんの応用問題が出題されやすく,受験生が苦戦しやすい範囲の一つだと言えます。そのためまずは基礎をしっかりと固めることを意識しながら,問題の特徴や出題傾向について抑えていきましょう。
体積とは?容積とは?
まずは基本的な事項の確認として,そもそも体積とは・容積とは何を指すのかといったことについてお話ししていきましょう。もちろんこの記事を読んでいる人の中には体積・容積の求め方を知っている人も多いでしょうが,その意味の違いをきちんと把握できている人は実は少ないのではないでしょうか。そこでまずは語句の解説から始めていきます。
初めに体積についてですが,こちらは物体が空間に占める大きさのことを指します。他方容積についてですが,こちらは容器の中に水をはじめとした物体がどれくらいの量入るかを表す数値のことを意味します。使われる単位もそれぞれ異なり,体積であれば立法センチメートル(cm3)や立方メートル(m3)が,容積だったらミリリットル(mL)やリットル(L)がつかわれますが,これらの意味の大きな違いは物体を見るときの視点の置き方にあります。体積というのは空間上に占める大きさのことを意味するので,空間という外側から物体を眺めているわけです。ところが容積の場合,物体の中身に注目しているので視点は外側からというより物体の内側に向けられます。
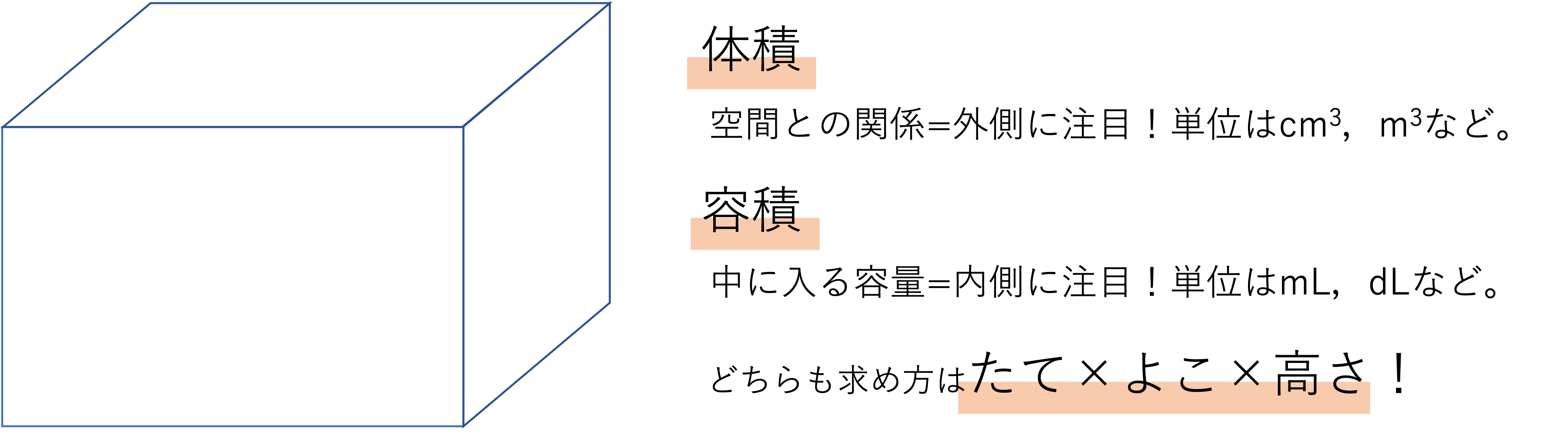
体積・容積と言われたらたて×よこ×高さという式だけを思い出す人が多いでしょうが,実はこのような違いがありました。意味の違いはさておき,使われる単位は少しでも違うと原点を食らうことがありますので注意していきましょう。その他の知識は受験に直接登場するわけではないですが,頭に入れておくと色々な問題が理解しやすくなります。参考にしてみてください。
水の深さと体積の問題の典型を覚えよう!傾き編
それではここからは水の深さと体積に関する問題の本格的な解説に移ります。初めにどのような問題が「水の深さと体積」に関するものなのか,ということを説明していきます。そえは,問題文の構造や特徴を知っておくだけで,回答スピードが大幅に向上するからです。今回はその中でも出題されがちな傾きに関する問題をご紹介しますので,まずはどこに注目すればいいのだろ・3問の共通点はどこだろう,などといったことに注目しながら目を通していただけますと幸いです。
1辺が15cmのふたのない容器ABCD-EFGHがあります。これに水を入れて,底面の頂点Hを固定して容器を傾けたところ,下の図のようになりました。このとき,容器に入れた水の体積は何cm3ですか。
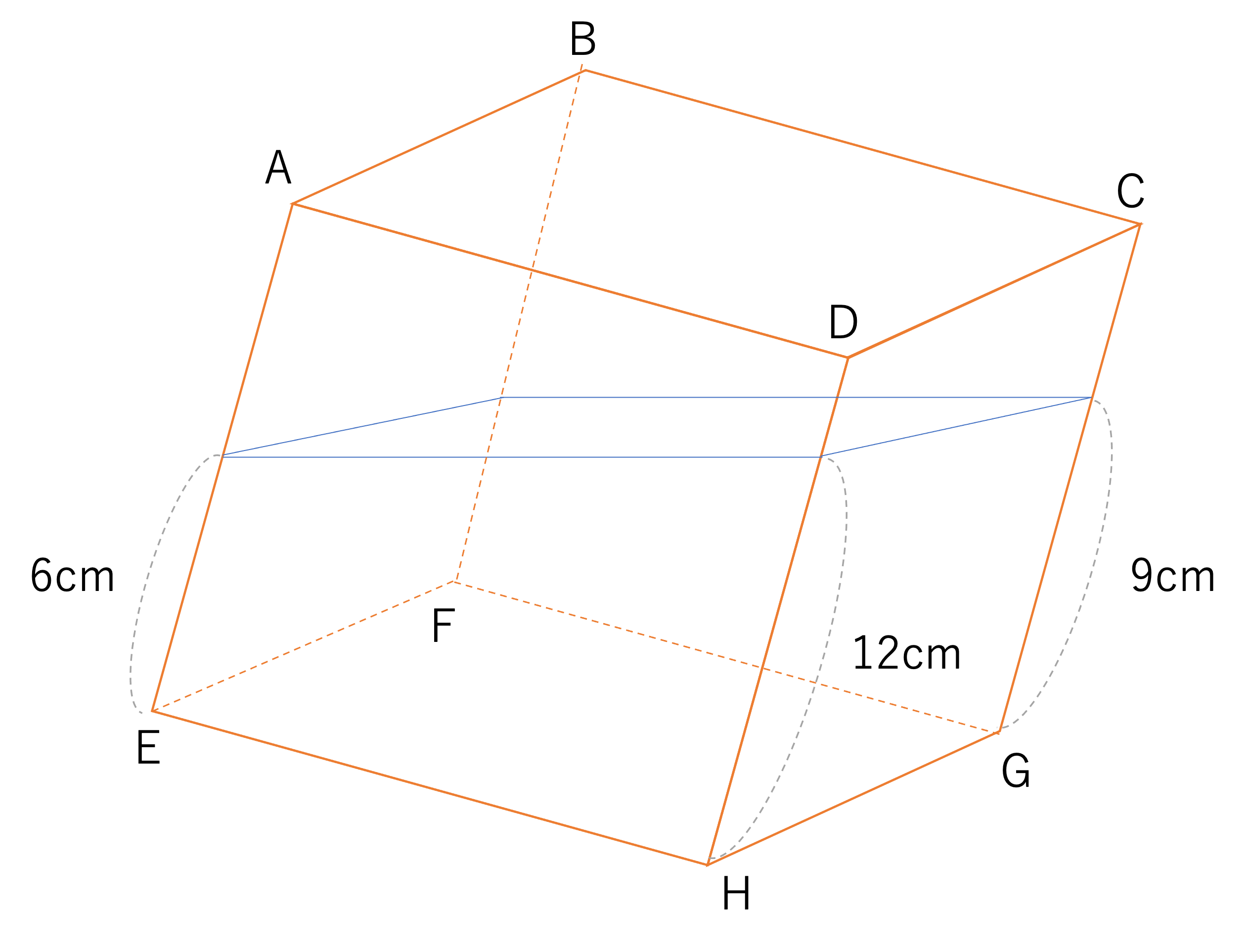
このような問題では水槽や容器が傾けられることから,一般的に水の傾きの問題と呼ばれることが多いです。今回取り扱っていくのは,このような問題の取り組み方です。このような問題の他にも,水槽に何かを沈めるときの様子だったり,L字やT字などの変な形をした水槽に水を入れる様子だったり,中にはそれらを組み合わせた問題もあります。それらの問題についても今後取り扱いますので,まずは傾きに注目して問題を解いていきましょう。
考えるポイントは立体の切断に!
さてここからは先ほどご紹介した問題を活用しながら,どうやって傾けた水の体積を考えていけばいいのかお教えしていきます。そもそも小学校で習った立体とはたて×よこ×高さで求められる直方体と立方体,底面積×高さで求められる円柱と角柱,人によっては底面積×高さ×3÷4で計算できる円錐や角錐だけでした。そのため上のような見慣れない立体が登場した場合,受験生の多くが手も足も出なくなってしまうのです。
しかし,このような立体を解く上でもいくつかの公式が存在します。今回はそれらの公式を紹介しながら,上の問題を解くことを狙いましょう。ここでご紹介するのは,ある平面で切断した立体の各辺に関する公式と,その辺を使って面積を求める公式の2つです。ある平面で切断された立体とは,わかりやすく言うならば平行な切り口がついている立体のことを指します。先ほどご紹介した図形も,よことよこの辺・たてとたての辺が平行になっていることから,平面で切断されているとみなすことができるのです。
さて,まずは各辺に関する公式ですが,こちらは向かい合った高さの辺同士を足すと同じ数になるという関係を表します。例えば下のように一つの平面で切断された立体において,辺の長さを順番にa,b,c,dと設定するとa+b=c+dという関係が成立するというわけです。この関係は特に体積や容積を計算する式の高さを導き出すタイミング,つまり計算の初めで使われることが多いです。知らないと全ての設問が解けない,なんてこともありますのでしっかり覚えておきましょう。
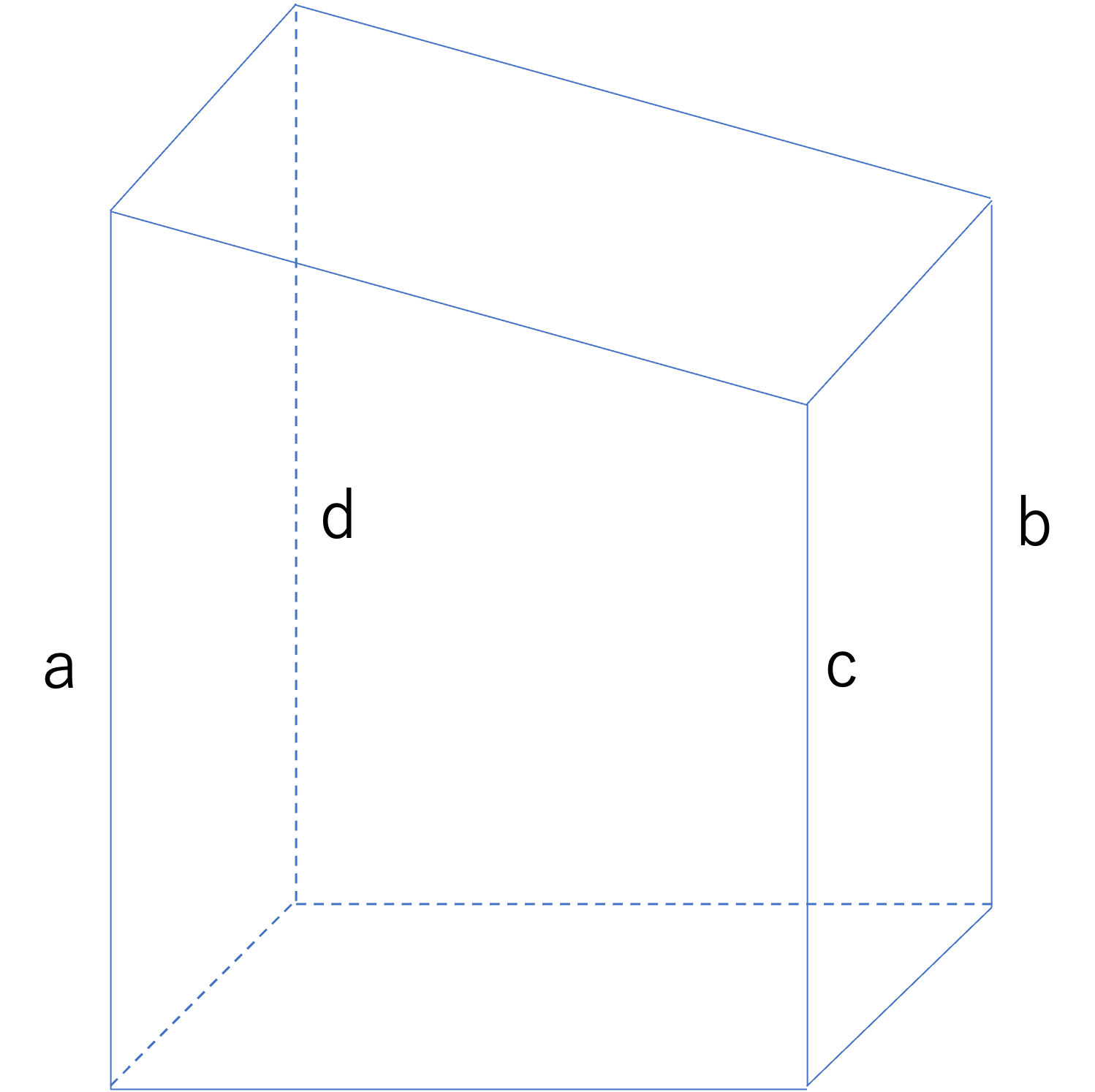
そしてこの各辺に関する公式を使うと,教科書には登場しなかったような立体でも体積・容積を計算することができるようになります。立体の体積・容積の求め方の基本はたて×よこ×高さ=底面積×高さでした。上のような立体において底面積は求められるとしても,高さが不明なので肝心の体積や容積を計算することはできません。しかし先ほど見たa+b=c+dの公式を使うと,体積や面積まで割り出せるのです。先ほどご紹介したこの公式は,実は同じ図形を2つ繋げたときに見えてくる関係性から見出されたものです。そしてこのとき,2つの図形を合わせて1つの図形だとみなすと,次のような式が成立します。
立体の体積×2=底面積×(a+b)=底面積×(c+d)
立体の体積=底面積×(a+b)÷2=底面積×(c+d)÷2
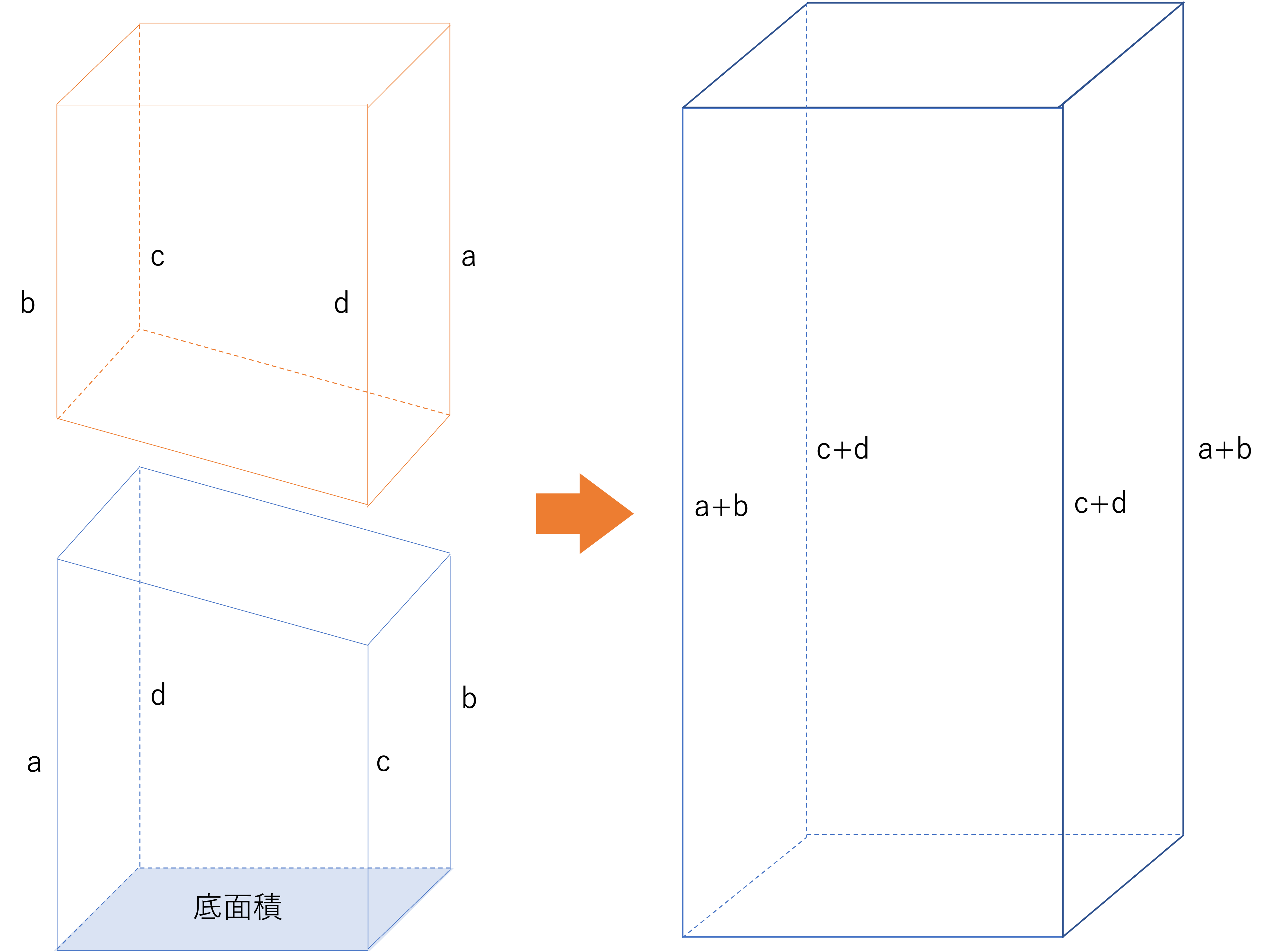
以上のことから,高さのないような立体についても体積・容積を計算することができるということがわかりました。このテクニックは水の傾き問題を使う上で大変有効であり,また他の立体の問題が登場したときにも役に立つものです。ぜひ頭に入れておきましょう。
例題を解いてみよう!
それではここまでお教えした2つの公式を使って問題を解いていきましょう。改めて問題をここで取り上げておきますので,どうやって計算すればいいのかを考えてみてください。
1辺が15cmのふたのない容器ABCD-EFGHがあります。これに水を入れて,底面の頂点Hを固定して容器を傾けたところ,下の図のようになりました。このとき,容器に入れた水の体積は何cm3ですか。

この問題において求められているのは,直方体でも立方体でもその他でもない立体の体積ですが,今回のテクニックを使えば簡単に解くことができます。このような図形において,体積は底面積×向かい合った辺の和÷2で計算することができました。今回の元々の立方体は1辺が15cmなので底面積は15×15=225cm2だと分かります。そして高さの部分ですが,今回は6cmと9cmの辺同士が向かい合っていることから,体積は次のように計算できます。ちなみにa+b=c+dの関係を使うと,立体の残りの1辺は3cmだということも分かります。以上のように大変計算をスムーズにしてくれるテクニックですので,この機会に覚えてしまいましょう。
体積=225cm2×(6cm+9cm)÷2=225×15÷2=1687.5cm3
終わりに
本記事ではこれまで,水の深さと体積の解説を扱う記事の第1段目として,水の傾きを解くときのポイントなどについてご紹介してきました。この範囲の問題は一癖ある形で出題されることが多いです。次回の発展編では入試問題を引用しながら実践的な攻略法について触れていきますので,ぜひそちらの記事にも目を通してみてください。本記事が今後の学習のお役にたてば幸いです。
















