この記事では、「 弁償算 」の解き方を学んでいきます。
読んで解き方を確認する、一緒に問題を解いてみる、どちらでも大丈夫なのでぜひ参考にしてみてください。

弁償算 とは
弁償算はつるかめ算と似ていて、つるかめ算の応用として紹介されることも多いです。
解き方もつるかめ算とほとんど同じなので、つるかめ算をマスターすれば弁償算も解けるようになると思います。
(つるかめ算について学びたい方はこちらの記事がオススメです。)
それでは、問題を見ていきましょう。
(例題1)A君はガラスのコップを100個運びます。1個運ぶごとに報酬として10円もらいます。しかし、コップを割ってしまうと1個につき70円弁償します。A君はコップを運び終え、760円もらいました。全部で何個のコップを割ったでしょうか。
ここからはこの例題を解きながら、弁償算の解き方について学習していきます。
弁償算 の解き方
はじめに、これからの解説をまとめた図を載せておきます。
-300x164.png)
これだけ見てもわからないと思うのですが、文章だけの説明でわからなくなったら戻ってきてみてください。簡単なメモ代わりです。
さて、例題を解く前に、まずはつるかめ算の解き方を思い出してみてください。
つるかめ算では、まず与えられた頭数が全てつるだと考えて、そこから一匹ずつかめにおきかえて考えるのでした。
ここでも同じようにまず、「すべてのコップを割らずに運べた」と考えてみましょう。するとA君は何円もらえるでしょうか。\(10\times100=1000\)(円)ですね。
しかし、実際には\(760\)円しかもらえていません。つまり、いくつかコップを落としてしまい弁償したということです。
そこで、つるかめ算のように\(1\)個をおきかえてみましょう。つまり、コップを\(1\)個割ってしまったと考えます。
このコップは運べていないので、報酬の\(10\)円はもらえません。おまけに\(70\)円弁償する必要があります。つまり、すべて運べた時と比べて\(80\)円だけもらえるお金が少なくなるということです。
コップを\(1\)個割り、\(99\)個を運ぶと\(80\)円だけもらえるお金が少なくなるということが分かりました。では、何個を割るともらえるお金が\(760\)円になるでしょうか。
\(760\)円ということは\(100\)個全て運べた時と比べると、\(240\)円だけもらえているお金が少ないですね。(\(1000-760=240\)) \(1\)個割るごとに\(80\)円もらえるお金が少なくなるので、\(240\div80=\)\(3\)(個)割ったということが分かります。 これが弁償算の基本的な解き方です。<例題1:解答)>
\(3\)個<例題1:別解>
今はすべてのコップを割らずに運べたと考えましたが、もちろん全てを割ってしまったとして考えることもできます。
.png)
全てを割ってしまうと、A君は\(70\times100=7000\)(円)弁償しなくてはなりません。ここから\(1\)個を置き換えてみましょう。
\(1\)個運べて、\(99\)個割ったときはどうなるでしょうか。報酬が\(10\)円もらえて、\(70\)円弁償しなくてよいので、\(80\)円弁償する金額が減ります。つまり弁償額は\(6920\)円となります。(\(7000-80=6920\))
実際には、\(760\)円もらっているので、すべて割ったときとの差は\(7760\)円です。(\(760-(-7000)=7760\))
よって、\(7760\div80=97\)(個)だけ運べた、ということが分かります。つまり、\(3\)個だけ割ったということですね。
このように、弁償算はどちらに合わせても解けるので、好きなほうに合わせて解きましょう。この問題では、コップを割りすぎてしまうとお金をもらえず、弁償しなくてはならなくなりそうですね。(報酬としてもらうお金<弁償代)
それを踏まえて、次の問題を解いてみましょう。
例題2
(例題2)例題1の条件でA君は何個以上コップを割るとお金がもらえず、弁償しなくてはいけないでしょうか。
(例題1:A君はガラスのコップを100個運びます。1個運ぶごとに報酬として10円もらいます。しかし、コップを割ってしまうと1個につき70円弁償します。A君はコップを運び終え、760円もらいました。全部で何個のコップを割ったでしょうか。)
↓
解答はこの下
↓
<例題2:解答>
\(13\)個以上<例題2:解説>
先ほど考えたように、すべてのコップを運べたときは\(1000\)円もらえ、\(1\)個割るごとに\(80\)円もらえるお金が減ります。
.png)
\(1000\div80=12\)⋅⋅⋅\(40\)(\(12\)、あまり\(40\))なので、\(12\)個割ると\(40\)円もらえます。
つまり、\(13\)個割ると\(40\)円の弁償です。\(13\)個以上割ると、どんどん弁償額が増えていきますね。よって、答えは\(13\)個以上となります。
もう1問解いてみましょう。
例題3
(例題3)数学の問題が10問あります。1問正解するごとに10点もらえますが、1問間違えるごとに3点引かれます。B君は9点でした。B君は何問正解できたでしょうか。
この問題は例題1(コップの問題)が解ければわかると思うので、ぜひ考えてみてください。
↓
解答はこの下
↓
<例題3:解答>
\(3\)問<例題3:解説>
解説をまとめたものがこちら↓
.png)
先ほどと同じように、まずは全て正解したと考えましょう。すると、\(10\times10=100\)(点)となります。
「\(1\)問正解するごとに\(10\)点もらえる」ということは、「\(1\)問正解から不正解にすると、\(10\)点引かれる」ということです。
「\(1\)問間違えるごとに3点引かれる」はそのままなので、全部正解のときから\(1\)問不正解を増やしていく度に、\(13(10+3)\)点引かれるということがわかります。
例えば、\(1\)問間違えて\(9\)問正解したとすると、\(13\)点引かれて\(87\)点となります。
これがわかったら、あとはB君が何点引かれたか考えればいいですね。
B君の得点は\(9\)点なので、\(100–9=91\)(点)引かれています。そのため、\(91\div13=7\)(問)間違えたとわかります。
問題は全部で\(10\)問なので、B君は\(3\)問正解したということが分かります。
検算すると、\(10\times3-3\times7=9\)(点)で一致します。
弁償算 の解き方のまとめ
これまで使ってきた弁償算の解き方をまとめると、以下のようになります。
- すべてどちらか一方だったと仮定する
(コップを全て運んだときは、〇円だ) - 1つ置き換えてみて、変化を調べる
(コップを1個割ったときは、□円引かれるな) - 問題で与えられた数にするために、何回変化させればいいか計算する
(△円にするには、何回コップを割れば(□円引けば)いい)
実は、これはつるかめ算の解き方とまったく同じです。
弁償算もつるかめ算同様面積図で解くこともできますが、つるかめ算とは少し違う図を書く必要があります。
また、問題を解くのが図を書く作業になってしまい、本質を理解しにくいので、この記事では面積図を使わない解き方のみをご紹介しています。
弁償算 の応用
応用問題として、少し難しい問題を解いてみましょう。
(応用例題1)じゃんけんをして負けたら階段を3段下り、あいこなら1段上がり、勝ったら5段上がるというゲームをC君とD君の2人でしました。15回じゃんけんをしたところC君は最初の位置から31段だけ上にいました。C君は何回勝ったでしょう。またD君は最初の位置よりも何段上または下にいるでしょう。ただし、C君のあいこの回数は負けた回数よりも2回だけ多かったです。
問題は難しくなりましたが、先ほど紹介した\(3\)ステップの解き方で解けます。 自分で解いてみたいという方は、ここで止めて解いてみてくださいね。
↓
解答はこの下
↓
<応用問題:解答>
- C君は\(5\)回勝った
- D君は最初の位置より\(1\)段下にいる
<応用問題:解説>
問題文が長くて複雑なので、\(1\)度整理してみましょう。
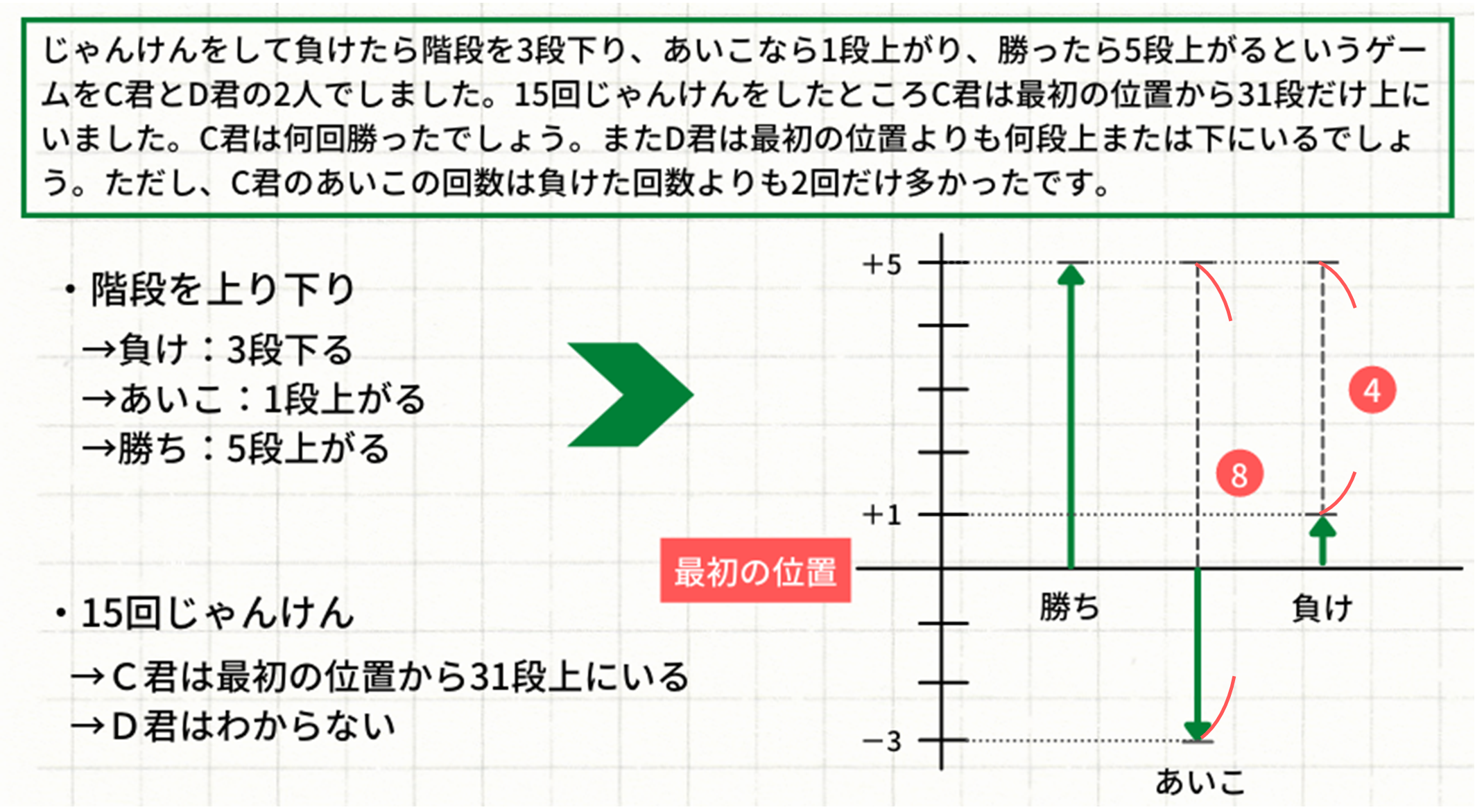
ここからは解き方に沿って解いていきます。
①すべてどちらか一方だったと仮定する
まず、C君がすべて勝ったと仮定してみましょう。
すると、最初の位置よりも\(5\times15=75\)(段)だけ上にいるはずです。
しかし、実際には\(31\)段だけしか上にいません。この差は\(75−31=44\)(段)です。
②1つ置き換えてみて変化を調べる
勝ちを負けにおきかえると、\(8\)段だけ下がります。勝ちをあいこにおきかえると、\(4\)段だけ下がります(上の図参照)。
ここで、負けとあいこの関係に注目しましょう。問題文に、「C君の負けた回数はあいこの回数よりも\(2\)回だけ多かった」とあります。ここから、C君は少なくとも\(2\)回はあいこになっていることが分かります。
.png)
では、\(2\)回だけあいこで、あと\(13\)回は勝ったとすると、C君はどこにいるでしょうか。
勝ち\(2\)回をあいこ\(2\)回におきかえるので、\(4\times2=8\)(段)だけ下がります。つまり、\(75−8=67\)(段)だけ上にいます。まだ問題文の\(31\)段よりも多いですね。
ここで勝ちをもう一回あいこにおきかえたいのですが、「C君の負けた回数はあいこの回数よりも\(2\)回だけ多かった」とあるので、あいこを\(1\)回増やすと、負けも\(1\)回増やす必要があります。
つまり、あいこ\(3\)回と負け\(1\)回にします。すると\(8+4=12\)(段)下がり、\(67−12=55\)(段)だけ最初の位置よりも上にいます。
あとは、勝ち\(2\)回を「あいこ\(1\)回+負け\(1\)回」に置き換えていけば良さそうです。この操作を一度すると、\(12\)段下がります。
これで変化がわかったので、あとは問題で与えられた数を求めるだけです。
③問題で与えられた数にするために、何回変化させればいいか計算する
「勝ち\(2\)回を『あいこ\(1\)回+負け\(1\)回』に置き換えると、\(12\)段下がる」ということがわかっています。
問題では「C君は最初の位置から\(31\)段だけ上にいました」とあるので、\(31\)にするために何回変化させればいいか計算しましょう。
.png)
あいこ\(3\)回のとき(あいこ\(3\)、負け\(1\)、勝ち\(11\))のときは\(55\)段だったので、\(55−31=24\)(段)だけ上にいます。
\(24\div12=2\)より、勝ち\(2\)回を「あいこ\(1\)回+負け\(1\)回」にする操作を、あと\(2\)回すれば良いと分かります。これを計算すると、あいこ\(5\)回、負け\(3\)回、勝ち\(7\)回となります。検算をすると、たしかに\(5\times7+1\times5−3\times3=31\)段となります。
もし上手く理解できなかった人がいたら、こちらの表を参考にしてもう一度解いてみてください。
ここまで分かれば、D君の位置を求めるのはおまけみたいなものですね。
.png)
D君の勝敗はC君の逆、つまりあいこ\(5\)回、勝ち\(3\)回、負け\(7\)回です。
D君が何段移動したか計算すると、\(1\times5+5\times3−3\times7=−1\)(段)となります。つまり、最初の位置よりも\(1\)段だけ下にいることが分かります。
最後に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。


















