今回の記事では時計算についてご紹介していきます。時計は小学1年生の頃から習う単元ですし,身近なところで触れるようなものであるのですが,受験生がなかなか苦戦することが多い範囲です。そのため本記事では基礎編として,時計の動き方や時計算とはどういうものなのか,といったことについて取り扱っていきます。
Contents
時計算とは?
攻略法の解説に進む前に,まずは時計算とはどういうものなのかということについて解説しておきましょう。簡単に言ってしまえば,時計算とはアナログ時計が登場する文章題のことです。しかし時計と言われても問われるのは時刻や時間などではなく,どちらかと言うと長針や短針といった針がなす角度についての問題です。つまり時計算とは図形の問題の1つなのです。実際に時計算と呼ばれる問題をいくつかご紹介してみると,以下の3つのようなものが挙げられます。「これが時計算か」と何となく把握しておくといいでしょう。
5時ぴったりのときに長針と短針が作る小さい方の角度は何度ですか。
3時から4時までの間で時計の長針と短針がぴったり重なる時刻は,何時何分ですか。
このような時計が作り出す角度をテーマに作られた問題が時計算です。1問目のような問題は解きやすいかもしれませんが,2問目のような問題はパッと解き方を思いつきづらいのではないでしょうか。そこで,ここからはまず時計の針の動き方や時計算で注目すべき点をご紹介していきます。
それぞれの針の動き方!
それではここからは時計の針の動き方について解説していきます。「普段から見ている時計の動き方なんて今更教えてもらわなくても」と思う方もいるかもしれませんが,角度という観点から見ることで初めて知ることもあるでしょう。完璧だという人は飛ばしてもらっても構いませんが,そうでない人はぜひ一読ください。
まずは基本的な用語の解説から始めていきましょう。そもそも時計には2つの針があります。そのうち一つが短針・時針と呼ばれる今何時かを指す針で,もう一つが長針・分針と呼ばれる今何分かを指す針です。この2つの針の組み合わせで,今現在の時刻が何時何分かを知ることができるわけですね。これらの用語の意味を把握できていないと時計算を解くことは難しいので,あまり馴染みがない人はこの機会に覚えてしまいましょう。なお,これ以外にも今何秒かを指す秒針という針も存在します。読者の皆様の家にある時計にはほとんどこの秒針が備わっているでしょうが,受験問題ではなかなか秒針まで出題されることはありません。そのため今回の記事では詳しく解説しませんが,たまに秒針が登場する問題もあると頭の片隅に入れておきましょう。
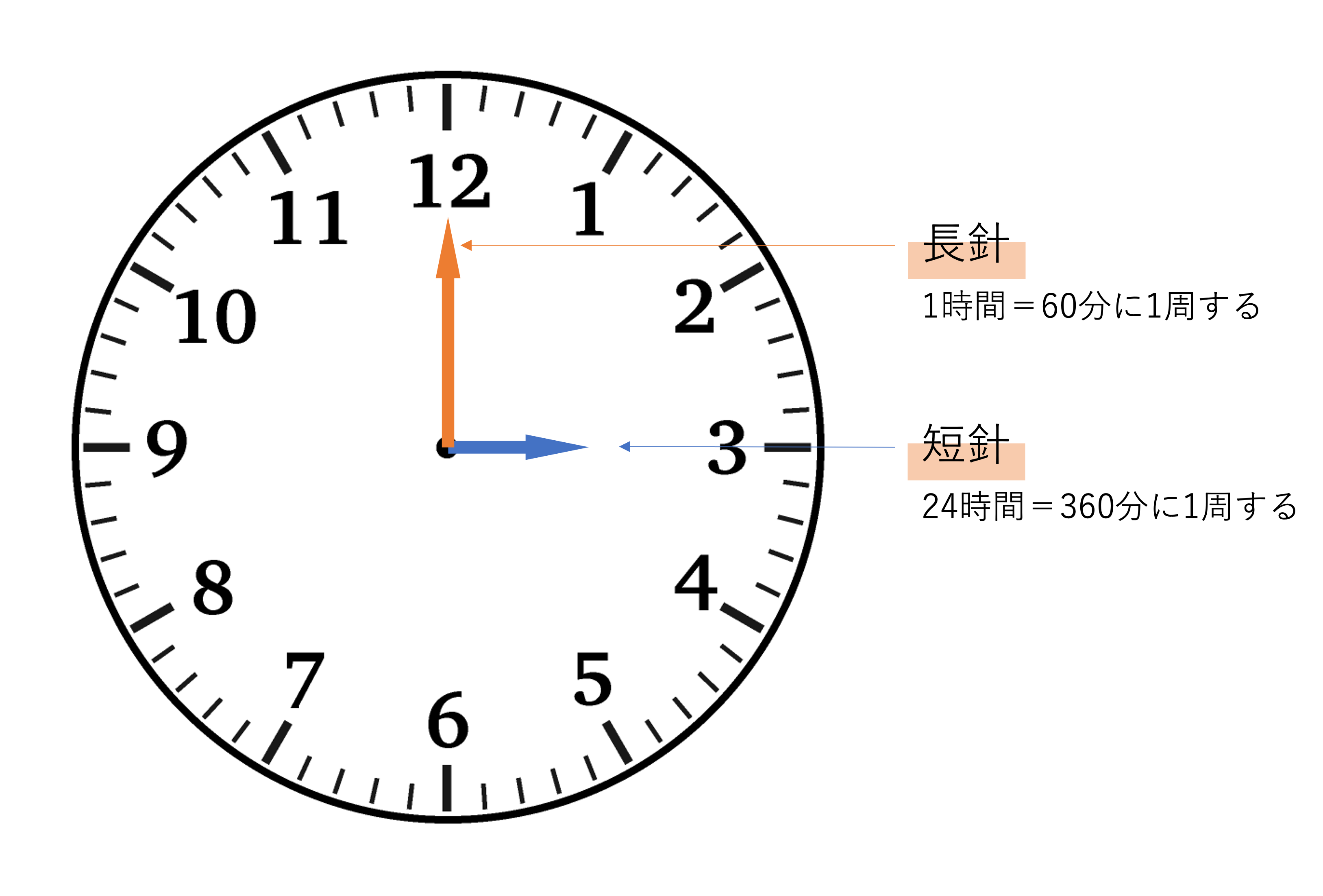
短針の動き方は…?
ではここからはそれぞれの針の動き方について詳しくみていきましょう。まずは短針からです。この短針とはご存知かとは思いますが,12時間で時計を1周します。1周するということは360°回転することを指すので,このことから短針は1時間で30°進むことがわかります。また1時間は60分であることから,短針は1分間で30°÷60=0.5°進むことも分かります。時計算では分刻みの回答が求められることが多いので,この1分=0.5°という公式は是非覚えておきたいところです。
長針の動き方は…?
続いては長針の動き方について説明していきます。長針は1時間に1周=360°進みます。ということは,長針は1分間に360°÷60=6°進むことが分かります。短針と長針の両方に当てはまることですが,1時間で進む角度と1分間で進む角度の両方を押さえておくことが大切です。後ほどご紹介していきますが,時計算では短針と長針の動きの差を考えなければいけないことが多いです。そのため忘れずに暗記しておきましょう。
大事なのは2つの針の関係!
短針と長針の動き方をご紹介したところで,続いては時計算を解く上で重要である2つの針の関係について学んでいきましょう。まずは1分あたりに進む角度の関係です。先ほど1分間に短針が0.5°・長針が6°進むとご説明しました。そしてこの2つの針が同じ方向に進んでいくことから,長針と短針が作り出す角度は1分間に6°-0.5°=5.5°変化していくと言うことができます。例えば12時に短針と長針が重なっていたとして,12時1分には短針と長針の間が5.5°開き,12時2分には11°開き,……といった具合で角度が変化していくわけです。もちろん2つの針の差は開いていくだけではなく,角度が小さくなっていくこともあります。問題のシチュエーションをよく理解した上で考えていきましょう。
また1時間あたりに変化する角度についても確認しておくと,短針は1時間に30°・長身は1時間に3600°進むのでそれらを足して390°ずつ変化していくことになりますが,このうち360°は1周分なので見かけ上は30°ずつ変化していく事になります。この30°の変化については近づく場合もあれば遠のく場合もあるので,こちらも問題文をよく読んで判断していくといいでしょう。
例題にチャレンジしてみよう!
それでは基本的な時計の動き方については概ねお教えできましたので,ここからは例題にチャレンジする事で,上で学んだ事項の確認を行っていきましょう。使用する問題は解説のところでご紹介したものですが,再度載せておきます。
(1)5時ぴったりのときに長針と短針が作る小さい方の角度は何度ですか。
(2)3時から4時までの間で時計の長針と短針がぴったり重なる時刻は,何時何分ですか。
解説!
(1)まずは1問目の解説です。この問題が一番取り掛かりやすかったのではないでしょうか。時計算で重要なことが問題文で紹介されている時刻を図に起こすということです。もちろん頭の中で時計の動き方を確認できるならそれに越したことはないですが,慣れるまではしっかりと図でイメージしていくといいでしょう。今回は5時ぴったりにおける角度と言及されているので,下のような図を書いてみましょう。今回求められているのは小さい方の角度ですので,その点は忘れないようにしておきましょう。
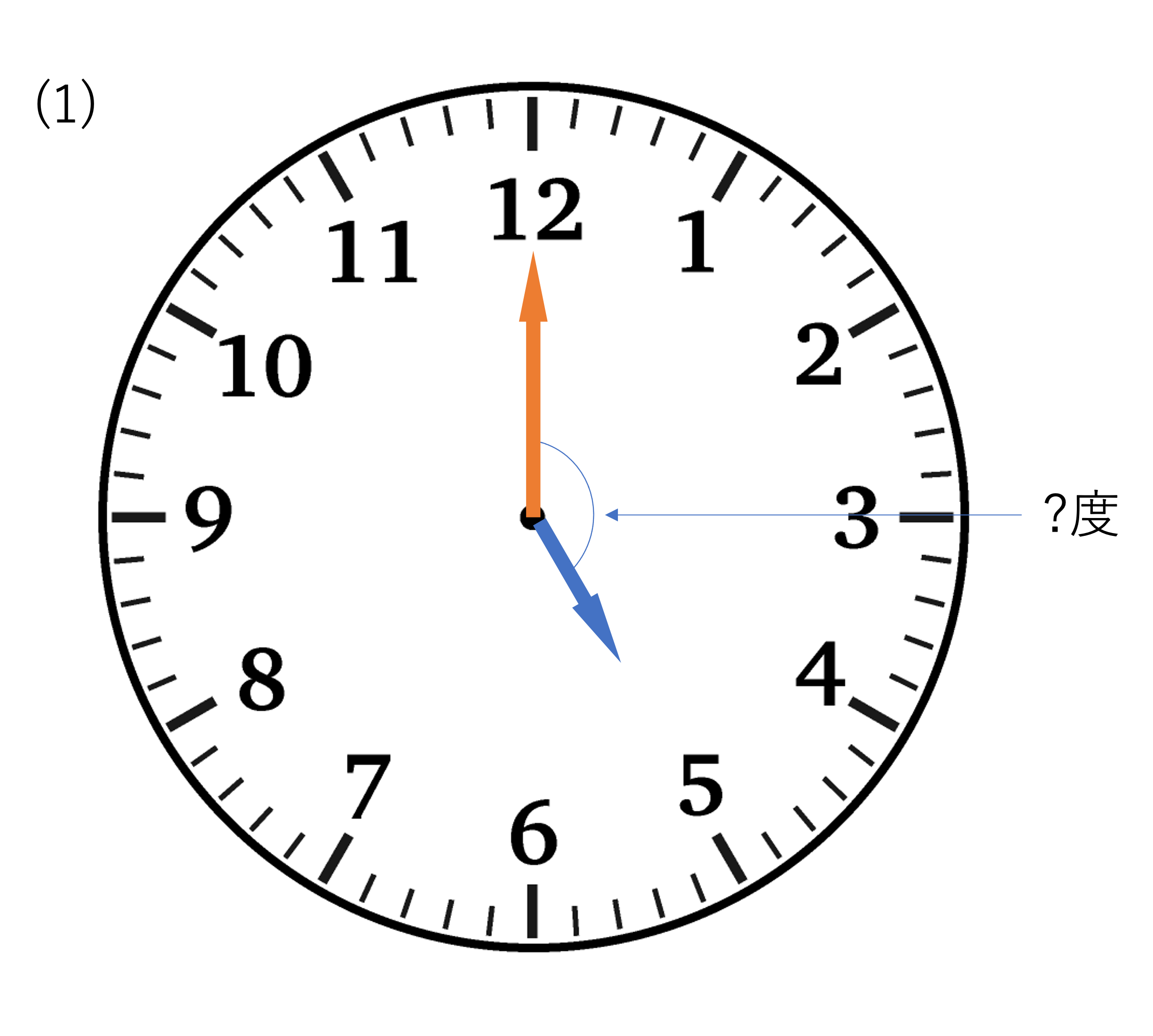
さてこの図から,今回求めればいいのは12から5までの間で作られる角度だということがわかります。ここで時計における1時間がなす角度は360°を12等分しているので30°になりますね。そしていま,5時ぴったりというのは1時間が作り出す角度が5個分集まっているとみなすことができ,このことから5時ぴったりのときに時計の長針と短針が作り出す角度は30°×5=150°となります。
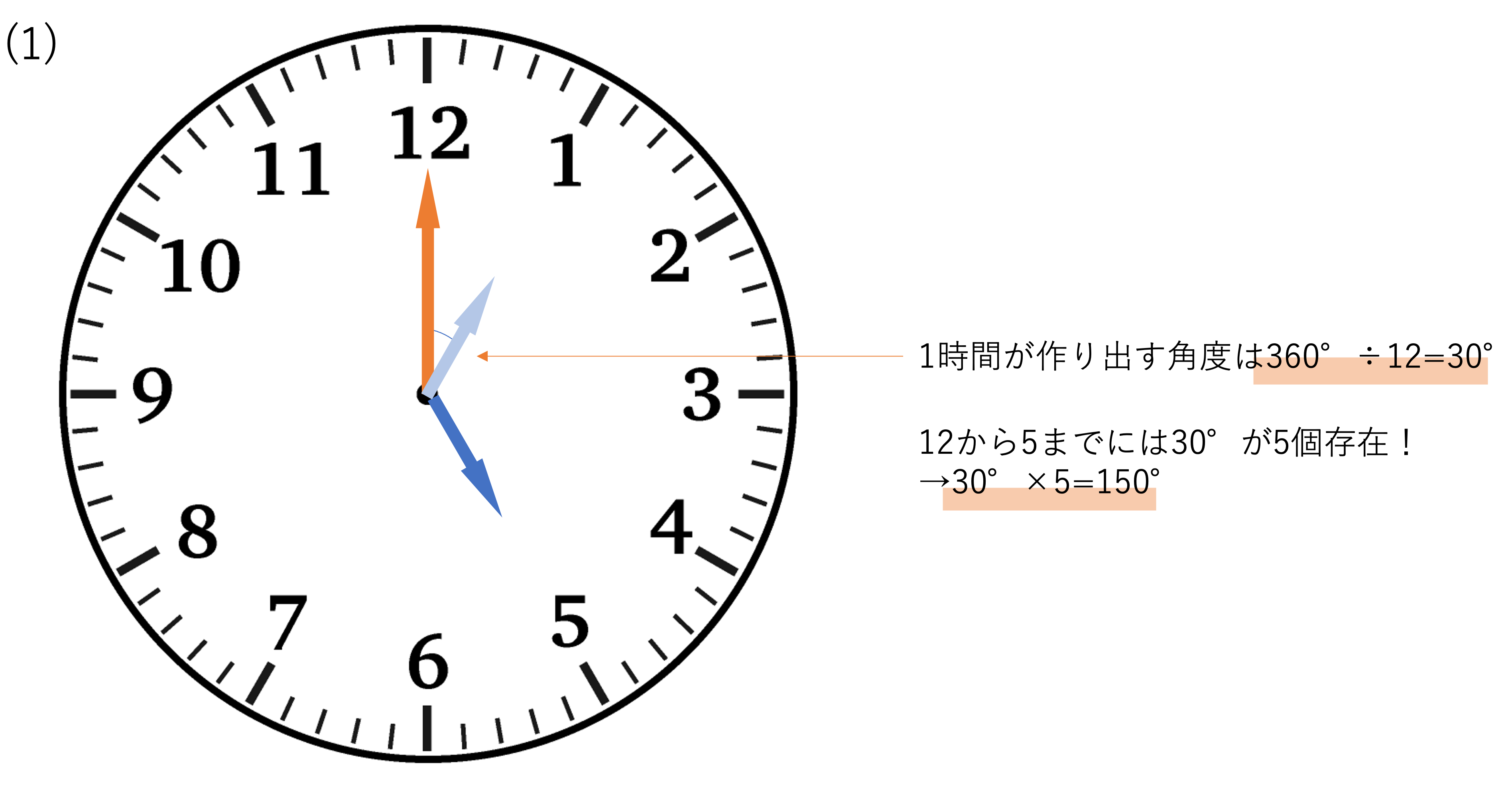
A.(1)150°
(2)続いては2問目の答え合わせになります。この問題では時刻が3時から4時までの間と設定されていたので,まずはそれらの時刻+ぴったり重なる時刻を図に書き出してあげましょう。
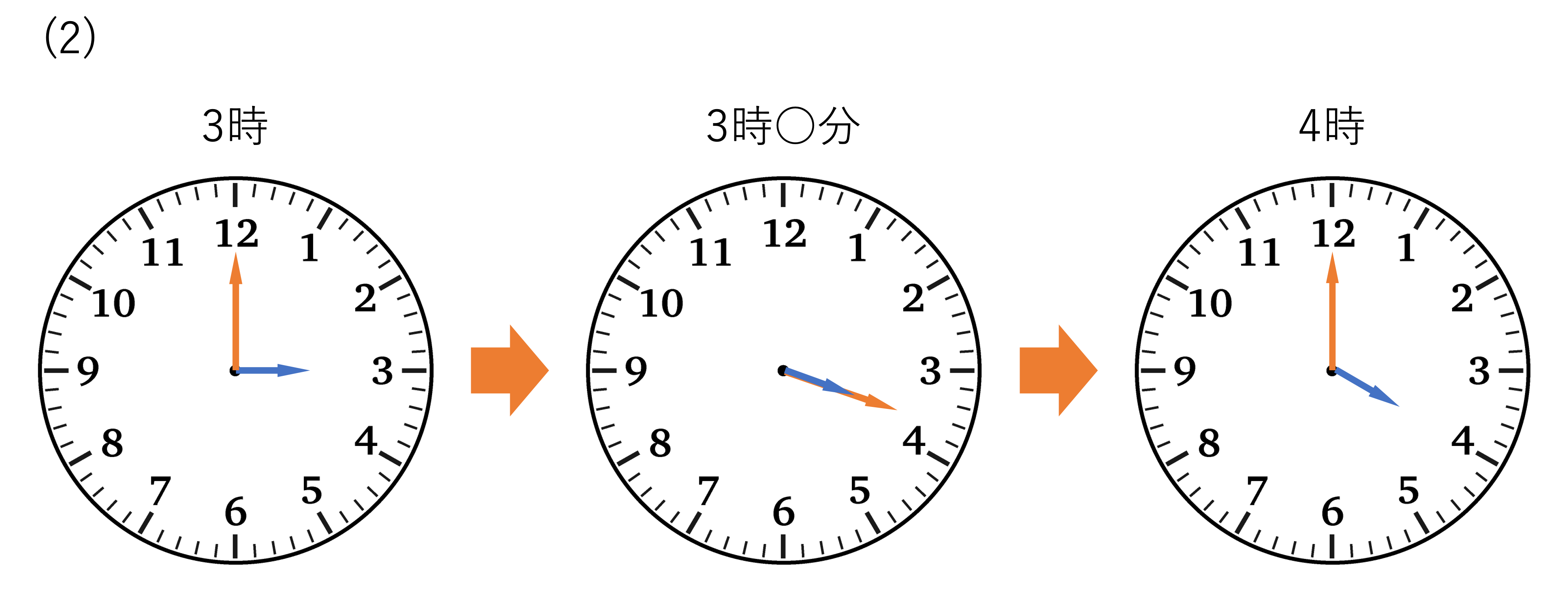
この図からもわかる通り,今回の問題で短針は3から4の間を動きます。そのため時計の2つの針がぴったり重なるときの時刻は3時台であり,しかもこのとき長針も3と4の間にいないといけないため,重なる時刻は3時15分から3時20分までのどこかということまで判断できます。この辺りは計算に直接関係するところではないですが,あとで確かめ算をするときに有用なので,ぜひ大体の答えを予想する癖を身につけておくといいでしょう。
さて肝心の計算ですが,このタイプの時計算のコツは元々2つの針が作っていた角度を基準に,その角度が0°になればぴったり重なると考えていくことです。今回は3時ジャストを基準としているので,(1)と同様の手順で計算を進めると2つの針が作り出す角度は90°だとわかります。そして上でお教えしたように長針と短針のなす角は1分間に5.5°ずつ変化していくので,3時1分には84.5°,3時2分には79°,……と作り出す角度が小さくなっていくわけです。これは旅人算などで登場する速さの関係と似ていますね。そのため計算式についても,速さの関係性を応用して次のように立てられるわけです。
1分間に変化する角度×分数=全体で変化した角度の総和
そして時計の2つの針がなす角度は1分間に5.5°変化しているので,以下のような計算の結果から答えが求まります。なお今回の問題では時間が分数を使った形で表される事になるため違和感を覚える人もいるかもしれませんが,実は時計算の答えでは分数が使われることが少なくありません。不安に思うでしょうが,そういうものなのだと割り切って答えるといいでしょう。
¥(90°÷5.5°=¥frac{90}{5.5}°=16¥frac{2}{5.5}=16¥frac{4}{11}¥)
¥(A.(2)3時16¥frac{4}{11}分¥)
まとめ
以上が時計算の解き方の基礎になります。ここで,最後に問題を攻略していく中で使用したテクニックをまとめておきましょう。時計算という文章題だからこそ有効なものもあれば,どんな文章題であろうと使えるコツもあります。たくさん演習をこなしながら身につけていきましょう。
- 短針と長針のなす角度は1時間に1回転+30°・1分間に5°変化する!
- 問題に出会ったらまずは時刻を図に表そう!
- 割り算を使って5.5°の変化が何回起こったかを計算しよう!
- 時計算では答えが帯分数になることも…!自信を持って答えよう!
終わりに
今回の記事では時計算についてご紹介してきました。冒頭で触れたように,この単元は所詮時計だろうと甘く見て取りかかりがちですが,思いのほか難しい構成や内容になっていることも多いです。そのため,早いうちから対策を心掛けておくといいでしょう。本記事が今後の学習のお役に立てば幸いです。