倍数算という文章題をご存知でしょうか。受験算数の文章題といえばつるかめ算が代表的ですが,その反面つるかめ算以外の文章題への対策は疎かになりがちです。今回はそんな倍数算の基礎についてお教えしていきます。よろしければ一読してみてください。
Contents
倍数算とは?
そもそも倍数算とはどのようなものを指すのでしょうか。名前だけ聞くとつい,「倍数という単語が問題文で登場する文章題だ」と思い込みがちですが,倍数算の倍数の由来は答えの導き方にあります。といっても言葉だけじゃわかりづらいと思いますので,ここでは軽くこんな問題があるという例をご紹介しましょう。
A君とBさんの所持金の比は5:4でしたが,A君がBさんに240円渡したところ,所持金の比は3:4になりました。はじめA君はいくら持っていたでしょうか。
このような問題が倍数算の例題になります。読んでいただけると分かる通り,倍数という単語は1回も出てきていませんよね。そのため倍数算とはパッと読んでわかりにくいでしょうが,2通りの比や割合が登場したら倍数算だと覚えてしまうといいでしょう。ちなみに2通りの比や割合とここで申し上げたのには,攻略にこのような数値を使うことが必要だからです。詳しい解き方は後々ご紹介します。
還元算・相当算との違いは…?
ところでこの倍数算の例題に関して,もしかしたら以前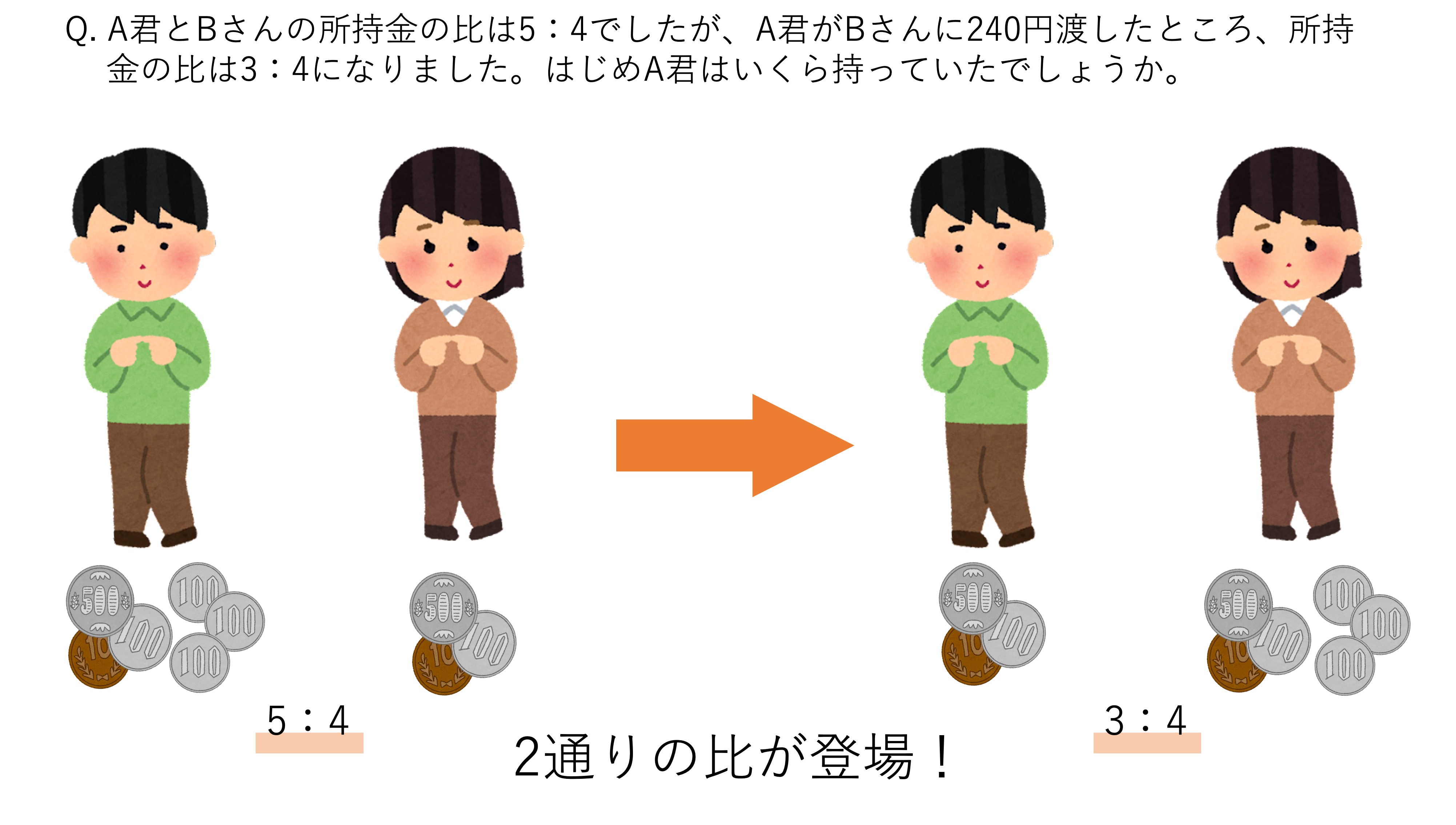 という別の記事で見かけたことがあるかもしれません。還元算・相当算というのは2つの異なる基準が登場する文章題なのですが,その中で先程の例題のような金額に関する比と数値が登場する問題をご紹介しましたね。このように還元算・相当算をある程度勉強している方だと,どちらで覚えればいいのか悩んでしまうことでしょう。
という別の記事で見かけたことがあるかもしれません。還元算・相当算というのは2つの異なる基準が登場する文章題なのですが,その中で先程の例題のような金額に関する比と数値が登場する問題をご紹介しましたね。このように還元算・相当算をある程度勉強している方だと,どちらで覚えればいいのか悩んでしまうことでしょう。
この倍数算と還元算・相当算ですが,実際のところこのどちらにも属する問題は存在します。倍数算の解き方は後述しますが,最小公倍数というものを考えていくのが倍数算であるのに対し,最小公倍数を使って考えた全体がいくつに相当するかを考えていくのが還元算・相当算という違いがある,つまり計算過程の中で注目する部分が違うだけなのです。そのため頭に入れやすい解き方や分かりやすい考え方で覚えてしまうのがオススメです。
倍数算の3パターン
ここからは倍数算の3つのパターンについて考えていきましょう。まずは倍数算の基本的な構造に注目していきたいのですが,先ほど述べたように倍数算には2つの比が登場しています。元々何らかの数の関係が1つの比で表されていたのが,ちょっとした変化が起きて別の比で表さないといけない関係になったという流れが倍数算で登場する基本的な要素になります。
そしてこの比の変化に関して,①数が増える・②数が減る・③数が増えたり減ったりする,という3つのパターンが存在すると言うわけです。ここでの数とは,比の関係で表されている数のことを指します。例えば先程の例題では所持金のついて話されており,2人の所持金が比で表されていました。そしてA君がBさんに240円渡した,つまりA君の所持金が240円減りBさんの所持金が240円増えたことで関係を表す比が変化しましたよね。つまりこの例題は③数が増えたり減ったりするパターンだった,というわけです。
解き方のコツ!
まずは問題文の分析!
それではここからは各パターンの攻略法を考えていきましょう。といってもこの3つのパターンはどれも線分図で同じように考えられますので,先ほど例題としてご紹介した③のパターンの攻略法を紹介しながら,残りの①・②の計算方法についてもセットで覚えてしまいましょう。
A君とBさんの所持金の比は5:4でしたが,A君がBさんに240円渡したところ,所持金の比は3:4になりました。はじめA君はいくら持っていたでしょうか。
まず倍数算を解く上で重要なのが,どのパターンの問題なのかを見分けることです。3つのパターンのうち,解かないといけない問題がどれに当てはまるのかを考えなければ図を書いたり整理したり計算を進めることもできません。今回の問題は先ほど確認したように③のパターンでしたが,誰のお金がいくら動いたのかに注意しておきましょう。
最小の状態を線分図に書こう!
そしてパターンが読めたら,次は問題文の整理に移ります。余談ですが,この分析→整理→計算という流れは全ての文章題に通じる考え方です。難しい問題でも,この一連の流れを心掛けておくだけで大変解きやすくなるでしょう。
さて問題文の中身を整理するのには,線分図というテクニックが有効に使えます。線分図とは,問題で登場した数量の関係を線で表したものです。以前別の記事でも何回かご紹介しているこの線分図ですが,倍数算でも使うことができます。
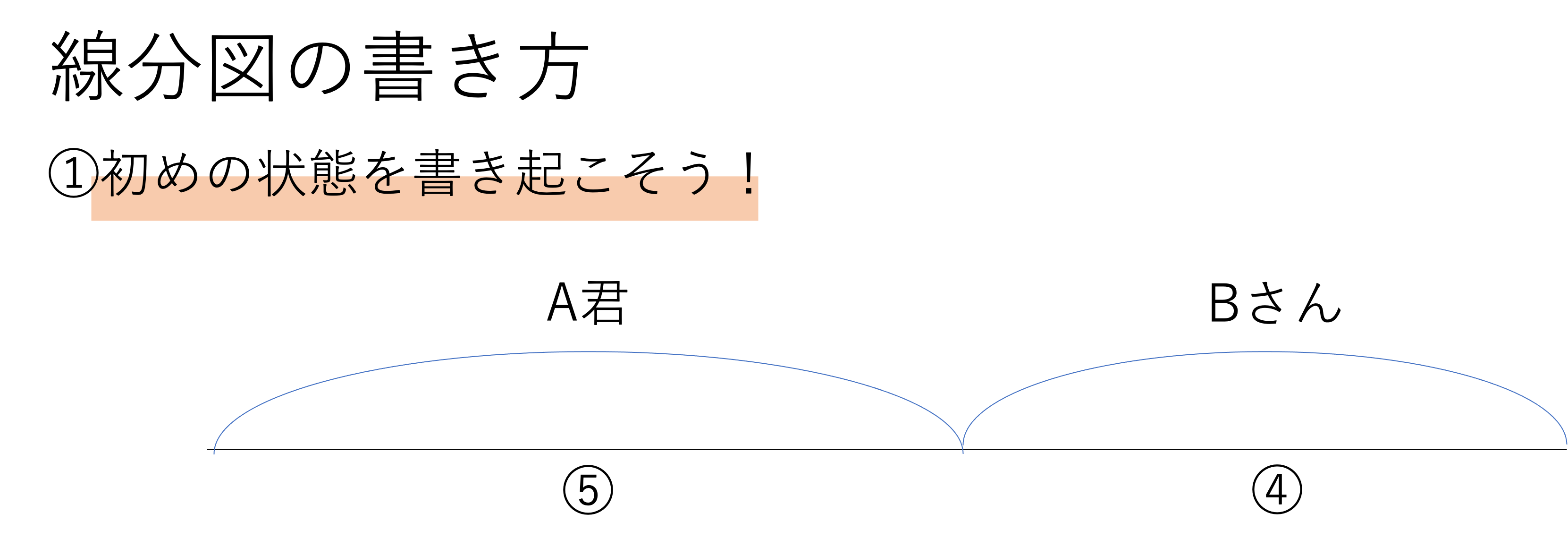
それではここからは線分図を書いていくのですが,まずは一番初めの状態を正確に図に表すことから始めていきましょう。今回の問題における初めの状態とは,A君とBさんの所持金の比が5:4であるということを指します。そしてそのことを下の図のように1本の線分で表しましょう。このとき,左右の線分の長さの違いは数量の違いを表すことを頭に入れておきましょう。違いはなんとなくでも構いませんが,厳密であればあるほど次のステップに進みやすいです。
やりとりの中身を記入しよう!
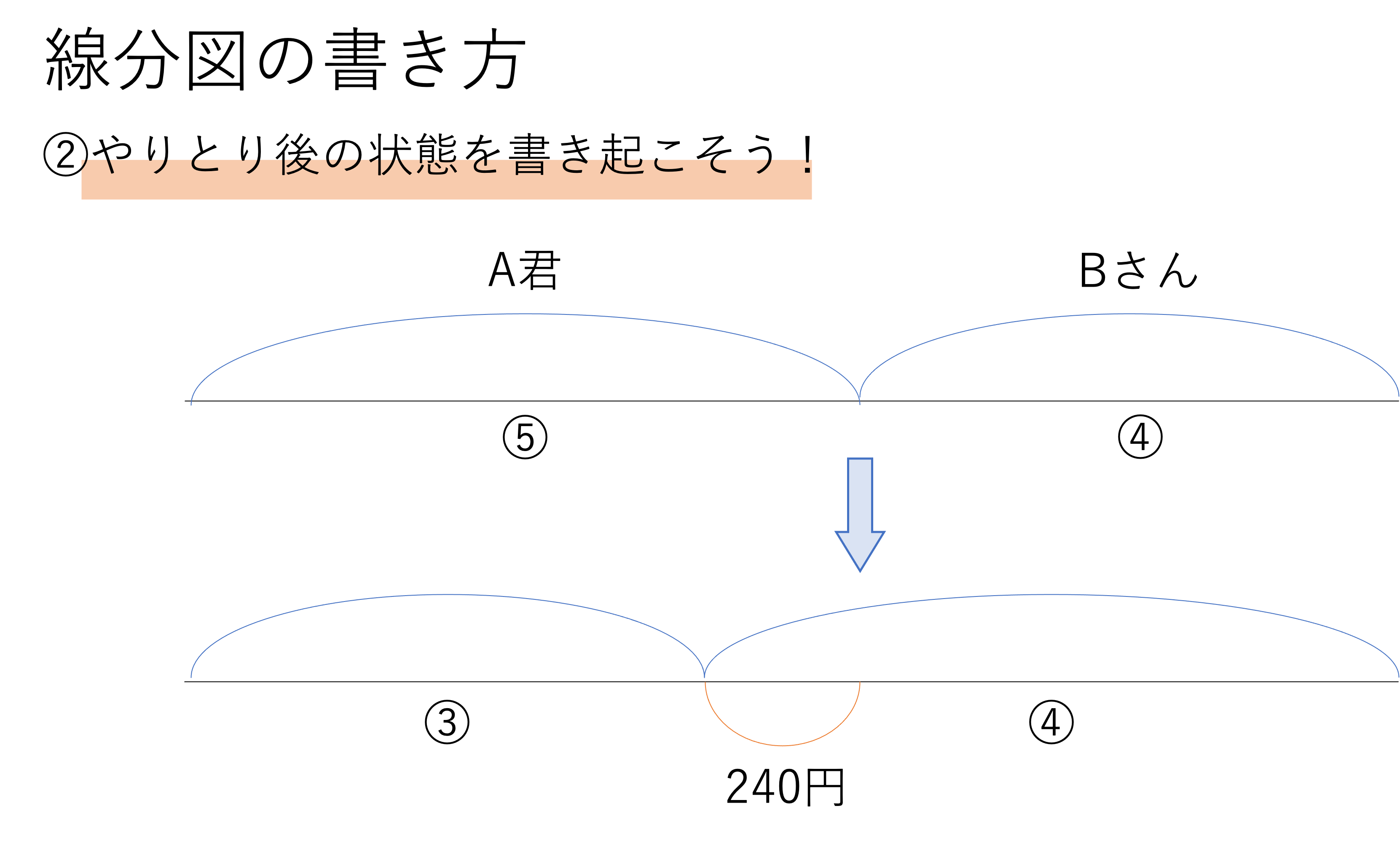
そうして初めの状態が書き表せたなら,今度はもう一本別の線分を書いて,A君がBさんに240円を渡した後の関係を書きましょう。このとき重要なのが,「渡す」ということをA君が240円失ってBさんが240円獲得した,と読み替えることです。こうすることでやりとりを反映させやすくなります。
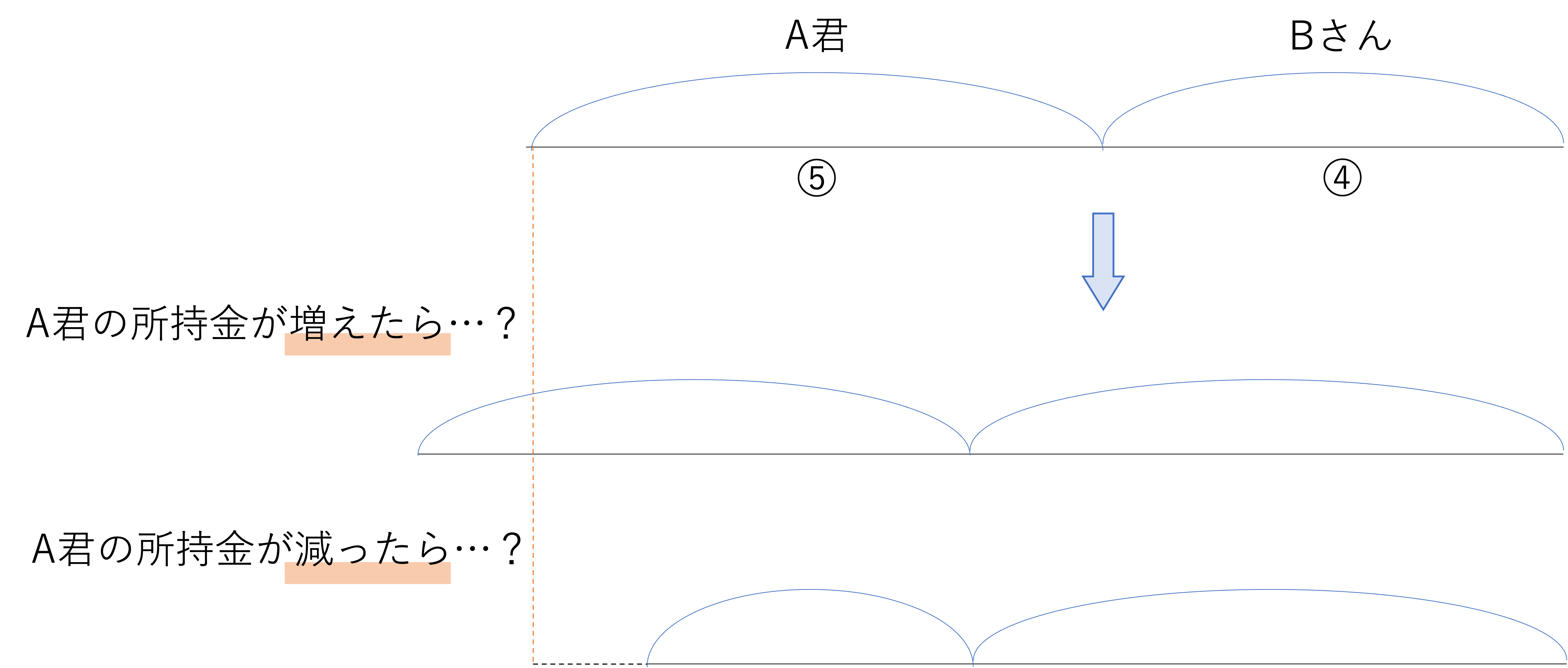
今回は③数が増えたり減ったりするというパターンだったので,A君の線分を短くしてBさんの線分を長くしたのですが,これが①片方が増える・②片方が減る,のいずれかのパターンだったらどうなるでしょうか。そのような場合は,線分そのものを短くしたり長くしたりしてしまえばいいですね。前述したように線分とは全体を表します。今回の全体とはA君とBさんが持っている所持金の合計であり,渡すという操作では全体での量が変わらないので同じ線分に書き起こしましたが,全体の所持金の量が変わるのであればもちろん線分の長さを変えてしまってもOKです。
数字と割合を比べよう!
そして次のステップが,この線分図に書き起こせた数字と割合を比べるということです。今回の問題だと数字は240円というものしか登場しなかったので,A君がBさんに渡した240円が全体のどれくらいの割合なのか,と考えていくことになります。そして240円と釣り合う割合が分かれば,その割合を大きくしたり小さくしたりしてA君とBさんの所持金が求められるというわけです。
しかしここで大きな問題とぶつかってしまいます。それが,お金を渡す前と後とでは比の割合が違うということです。今回の問題ではやりとり前の比が5:4,つまり全体が9になっていましたが,やりとり後は比が3:4,つまり全体が7になっていて,同じ「1」が示す中身が変わってきます。そのためここで必要になってくるのが比の分母を揃えるという作業です。
比の分母を揃えるとは,それぞれの比の和である9と7を最小公倍数の63で揃えるということです。このように倍数の考え方を使用することから,この文章題が倍数算と名付けられているのですね。そして分母を63に揃えて改めて線分図を書き直すと次のような図が完成します。
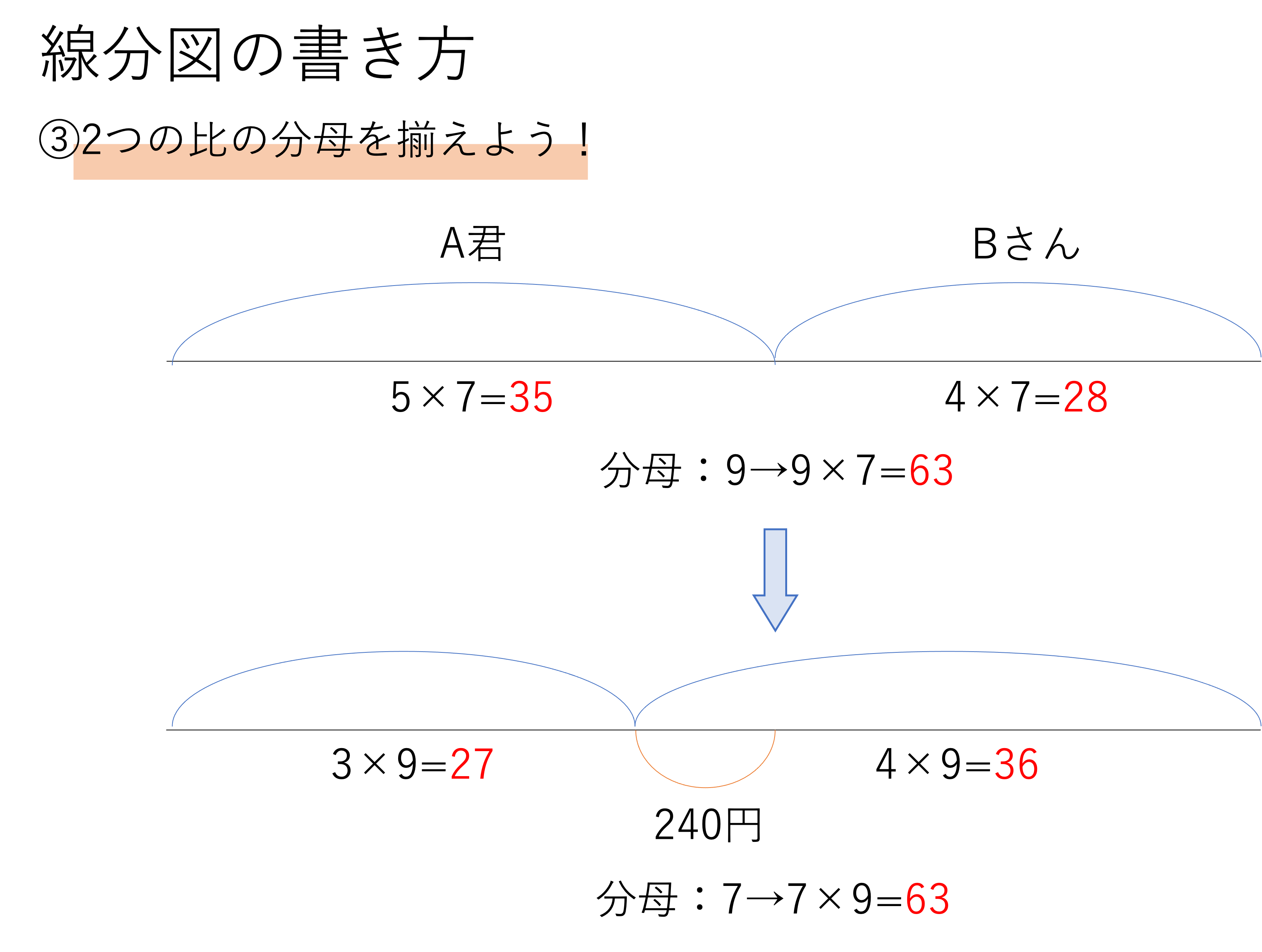
このように図を書き起こすと,240円が一体どれくらいの割合なのかが分かってきますよね。240円はA君が失ったお金なので,A君の所持金が減った割合を考えれば,その部分の割合も計算できるというわけです。いま最初のA君は63という全体のうち「35」を持っていましたが,渡した後は「27」に減ってしまいました。その差は8なので,240円という数字は全体を63と捉えたときの8に相当することが明らかになります。以上のことから,この線分図の中の「1」という比がいくつに値するのかが求められます。
8:240=1:30
このことから「1」の中身が30円だと分かりました。そして今回問われているのは初めのA君の所持金であり,A君は初め全体のうち「35」の所持金を持っていましたから,答えは次のようになります。
30×35=1050
したがって答えは1050円となります。
A.1050円
このような流れを踏むことで倍数算は攻略できます。最後に改めて問題を解く手順と整理しておきましょう。迷ってしまったらこのまとめを見ながら確認しておくと良いでしょう。
- まずは問題文の分析!
- 最初の状態を線分図に起こす!
- やりとり後の状態を別の線分図に起こす!
- 比の分母を揃えて数字と割合を重ね合わせる!
- 「1」の大きさから答えを求める!
まとめ
今回の記事では「倍数算とは何か?」という説明から始めていき,線分図を使った解き方をお教えしていきました。記事の中で用いた例題は初歩的なものですが,それでも倍数残攻略のエッセンスが詰まっています。より高度な問題を解いてみたい方がいましたら,おすすめ記事や参考文献,または後日更新する続きの記事をご覧ください。本記事が学習の手助けとなれば幸いです。

















