本記事は場合の数・確率の攻略法!【基礎編】の続きの記事となっております。前回の記事で場合の数とは・確率とは,という基本的な事項を確認した後,実践的な解き方のテクニックとして樹形図での計算,および樹形図をもとにしたかけ算による計算をご紹介しました。もしこの単元が全くわからない,という場合にはこの記事を一読してみてください。
場合の数・確率に関する問題はどんな学校でも,そして大問でも小問でも出題されやすいです。今のうちから基礎の部分を抑えておき,周りの受験生と差をつけてしまいましょう!
基本事項の確認
場合の数をおさらい
今回は余事象の考え方をお教えしたいと思いますが,まずはその前に場合の数とは何か・樹形図とは何かを確認していきます。次の場合の数に関する問題を解いてみましょう。下に解説がありますが,まずはご自分の力で解いてみてください。
表と裏のあるコインを3回投げたとき,コインの目の出方は全部で何通りありますか。
では解説していきます。といってもこれは樹形図を書くことで答えを導けますね。樹形図とはある数字やマークの並び方を1から順番に数え上げていくものでした。左から右へと枝分かれしていくことで,並びを可視化することができます。今回は一番左の列に,1回目で表が出るか裏が出るかを書きましょう。
次に2回目にコインを投げることを考えましょう。このときも表か裏かのどちらかが出ます。そのため例えば1回目に表が出たとき,2回目に表が出る場合と裏が出る場合が考えられます。同じように裏が出る場合も,2回目に表が出る場合・裏が出る場合が考えられ,合計で4通りの並びが表れるわけです。3回目もこれと同様に考えると,樹形図は下のようになります。
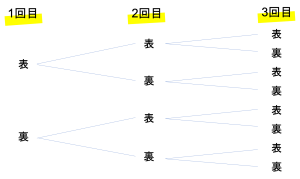
この図を見ると,最終的に枝が8つに分かれていることがわかります。したがってこの問題の答えは8通りです。もちろんこのとき,1回目・2回目・3回目とも表か裏かの2通りの場合が考えられるから,2通り×2通り×2通り=8通りと計算しても大丈夫です。むしろかけ算で簡単に計算できたのであれば,それはこの単元をよく理解できていることの証拠でしょう。
A.8通り
ここまでは基本的な復習でしたので,樹形図の考え方を知っていれば比較的簡単に解けたのではないでしょうか。この問題を元に,余事象の考え方を覚えていきましょう。
余事象とは?
ここからは余事象について説明していきます。まずその意味をお教えし,その後例題を通じて考え方を定着させていきます。
まず余事象とは,全体の場合の中である特定の条件に当てはまらない事象のことを指します。これだけだと伝わりづらいのでいくつか例を出しましょう。例えば表と裏のあるコインを投げるとして,表が出るという場合に対する余事象は,表が出ないときのことを指す,といったような具合です。このように求められている特定の場合のうち,そうじゃないほうが余事象の意味になるのです。ちなみに事象の意味は出来事と同じです。

ただしこの余事象は中学校になってから本格的に習うことです。難しいな,と思うのが当然とも言えます。その場合は下でご紹介する解き方のテクニックだけ覚えてしまいましょう。
この余事象,つまりはそうじゃない事象を考えることが問題に答える近道につながります。どのように使えるのかを説明していくため,まずは上の例題を少しいじった問題を解いていただきます。
表と裏のあるコインを3回投げたとき,少なくとも1回は表が出る場合の数を求めなさい。
いかがでしょうか?このように問題文に少なくともという言葉が出てきたら余事象の考え方を使うサインだと思ってください。今回まだ余事象に不慣れな人は,おそらく次のような樹形図を作ることで問題を解いたことでしょう。
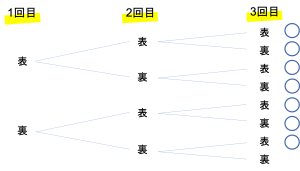
例題で登場した樹形図のうち,条件に当てはまるものに印をつけました。少なくとも1回とはつまり1回以上表が存在することを指すので1回目・2回目・3回目のどこかで表が出るものは条件に合いますね。したがって7通りが当てはまることになります。
A.7通り
これを余事象の考えを使って解くとどのようになるでしょうか。余事象とは特定の条件「じゃないほう」の場合のことを指しました。今回の「少なくとも1回表が出る」事象の余事象は,「1回も表が出ない」になります。1回も表が出ない事象はいくつあるでしょうか。
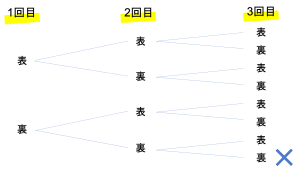
この×が1回も表が出ない並びを表します。よって余事象は1通りです。ここで全体の場合の和は8通りあるので,8通りから「じゃないほう」の1通りを引くと,7通りという数が表れます。このことから,少なくとも1回表が出る場合は7通りという答えが出るのです。これが余事象の活用になります。
このように全ての場合の数から余事象の数を引くことで特定の場合の数が求まる,というのが余事象を用いたテクニックになります。今回は樹形図で考えやすい問題でしたが,問題によっては数えても数えてもキリがないような条件を与えられることもあります。そのようなときに余事象の考え方を使うと,簡単に手早く答えを導けるのです。
全ての場合の数−余事象の数(「じゃないほう」の数)=特定の場合の数
余事象の確率
上では余事象の考え方と,それを使った問題の解き方をご紹介しました。実はこの余事象の考え方は場合の数だけでなく確率の計算でも活用できるのです。確率とは特定の場合の数を全ての場合の数で割った値のことでした。このことから確率の分子を計算する上で余事象の考えは有効に働くのです。先程と同じ問題を使って,今度は確率を計算していきましょう。
表と裏のあるコインを3回投げたとき,少なくとも1回は表が出る確率を求めなさい。
先程と同じ問題ですので,樹形図は省略していきます。この問題で全体の場合の数は8通りであり,少なくとも1回は表が出る,という条件に当てはまるのはこのうち7通りでした。したがって答えは\(\tfrac{7}{8} \)になります。
ではここで余事象の考え方を使うとどのように計算できるのでしょうか。先の説明で,全ての場合の数−余事象の数(「じゃないほう」の数)=特定の場合の数と解説しましたね。この公式を使うと,確率の分子に来る特定の場合の数が求めやすいのです。全体の8通りのうち「じゃないほう」の1通りを引くことで,表が出るものを数え上げるよりも簡単に計算を終わらせることができます。

このようにある特定の事象が発生する確率を求めるとき,余事象に注目した方がいいパターンもあります。今回は条件に合うものが7通りしかなかったので数えやすかったとは思いますが,解き方の一部として覚えておくといいでしょう。
A.\(\tfrac{7}{8} \)
問題を解いてみよう
それではここまででお教えした余事象の考え方を使って,実際の入試問題を解いてみることにしましょう。今回は標準的な難易度のものを引用しましたので,よろしければ自分の力だけで解けるか挑戦してみましょう。
白,黒,赤の球がそれぞれたくさんあります。これらの球の中から3個をランダムに選んで左から1列に並べていくとき,その並べ方は何通りあるか求めなさい。ただし,白または黒の球の右どなりに球を置くときは,赤の球しかおけません。
(関西学院中等部(2020),一部改題)
解説
答えを無事導けたでしょうか?ここからは問題の解説をしていきます。今回は3種類の玉を並べていく問題でしたね。ただし白・黒の隣には赤色の球しか置けないという制限がありました。この条件に合う並び方を数えていくのも悪くはないですが,樹形図に全ての並びを書き出して白・黒の隣に赤以外の球を置いている並びを弾く,というやり方で解いてみましょう。
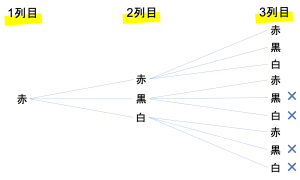

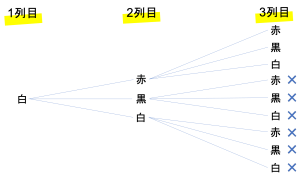
全ての並びを考えていくと,上のような樹形図がかけました。×は白か黒の隣に赤以外の球が並んでいるもの,つまりは余事象になります。×は全部で16個の並びについたので,余事象は16通り存在することがわかりました。
各列に置かれる球が赤・黒・白の3通りあるため,全体の場合の数は3×3×3=27通りです。このうち16通りが余事象であるため,問題にある白または黒の球の右どなりに球を置くときは,赤の球しかおけませんという条件を満たすものは27-16=11通りです。したがって答えは16通りとなります。
このように数えるべき場合が多いとき,当たりのものを探すより外れの余事象を考える方が答えを導きやすいこともあります。両方の解き方を身につけておきたいところです。
A.16通り
まとめ
今回は簡単に素早く問題を解くための余事象の考え方をご紹介し,例題を解きながら解答のためのテクニックを身につけていく,というものでした。前述したようにこの考え方は中学校に入ってから本格的に学習するものですが,覚えておくと受験において有利に働きますので,演習を積んで慣れておきましょう。本記事が学習の手助けとなれば幸いです。
(ライター:大舘)
おすすめ記事
参考
・父ちゃんが教えたるっ!「場合の数の便利技〔余事象〕」. 最終アクセス:2021/02/14


















