今回の記事では,速さと比について扱う記事の第三段目として,実際に受験で出題された問題を引用しながら応用的な攻略方法についてご紹介いたします。
前々回の基本編の記事では速さについての基本的な考え方を,前回の発展編の記事では3つのパターンの基本的な解き方をご紹介していますので,よければそちらも参照しながらお読みいただけますと幸いです。
Contents
発展編振り返り!速さと比の解き方とは?
ではまず前回の発展編の内容を振り返っていきましょう。
発展編では速さと比の文章題を,道のりが一定の場合・時間が一定の場合・速さが一定の場合の3つのパターンに分け,それぞれの攻略法を解説していきました。
このとき全てのパターンで共通するのが,はじめにどの部分が一定となっているかを確認し,確認した情報を線分図に整理した上で,2つの式を立てるというステップを踏むことの重要さです。
このような攻略法は他の文章題でも有効なのですが,こと速さと比に関しては情報がまとめられず苦戦することが多いので,いつも以上に意識していただけますと幸いです。
また分速・時速,m・kmなどの単位を揃えるということも同じくらい重要です。計算が合っていても単位の間違いで×がついてしまうことも多々ありますので,最後まで気を抜かないように,といったことをお話ししましたね。
加えて,道のり・速さ・時間が一定である場合の残りの2つの要素の関係についてもご説明しましたね。
- 道のりが一定になるときは時間と速さの比が反対になる
- 時間が一定になるときは道のりと速さの比が同じになる
- 速さが一定になるときは道のりと時間の比が同じになる
この3つの関係は覚えておくと問題を解く上で大変便利です。もちろん覚えきれていなくても上の攻略法をなぞっていけば答えは導けますが,中学受験は時間との戦いです,1分1秒を無駄にしないためにも,比の関係は覚えておくといいでしょう。
以上の攻略法・コツを活かしながら,問題演習を進めていただけますと幸いです。
問題① 標準的な文章題!
ここからは問題演習に移りましょう。まずは肩慣らし程度に頻出されるレベルの問題をご用意しましたので,発展編の中身を思い出しながら解き進めていただけますと幸いです。
あつし君は毎朝同じ時刻に家を出て学校へ行きます。分速90mで歩くと8時25分に着きますが,自転車で分速300mで行くと8時11分に着きます。あつし君が毎朝家を出る時刻は何時何分ですか。
(高輪中学校(2017),一部改題)
解説①
それでは解説に移ります。1問目ということで慎重に進めていきましょう。
まずは道のり・速さ・時間のうち一定となっている要素を探していきます。今回の問題では,あつし君が家から学校まで行くときに,進む速さを変えると登校にかかる時間が変わるという状況が設定されています。
このことから,家と学校の距離が日によって異なるなんてことが起こりえない以上,毎朝の登校についての話がなされているということはあつし君の進む道のりが一定であることが明らかになりますね。
そして道のりが一定であるということが分かったら,ここからはその情報をもとに線分図を作っていきましょう。前回の記事でも紹介しましたが,速さと比における線分図では道のりを線分で表すと整理が簡単です。
今回は道のりが一定であるため,1本の線分図を作っていきます。ここであつし君が進む速さは文中で示されていますが,家を出る時間がわからない以上,かかった時間がわかりませんね。そこで今回は歩いて登校するのにかかった時間を□分として図を作っていきましょう。なお歩きで□分かかって8時25分に着いたということは,自転車で登校して8時11分に着いた場合にかかった時間は(□-14)分と表せますね。
このようにして,分からない部分がある場合には□で置き換えながら進めていくと,次のような図が作れるはずです。
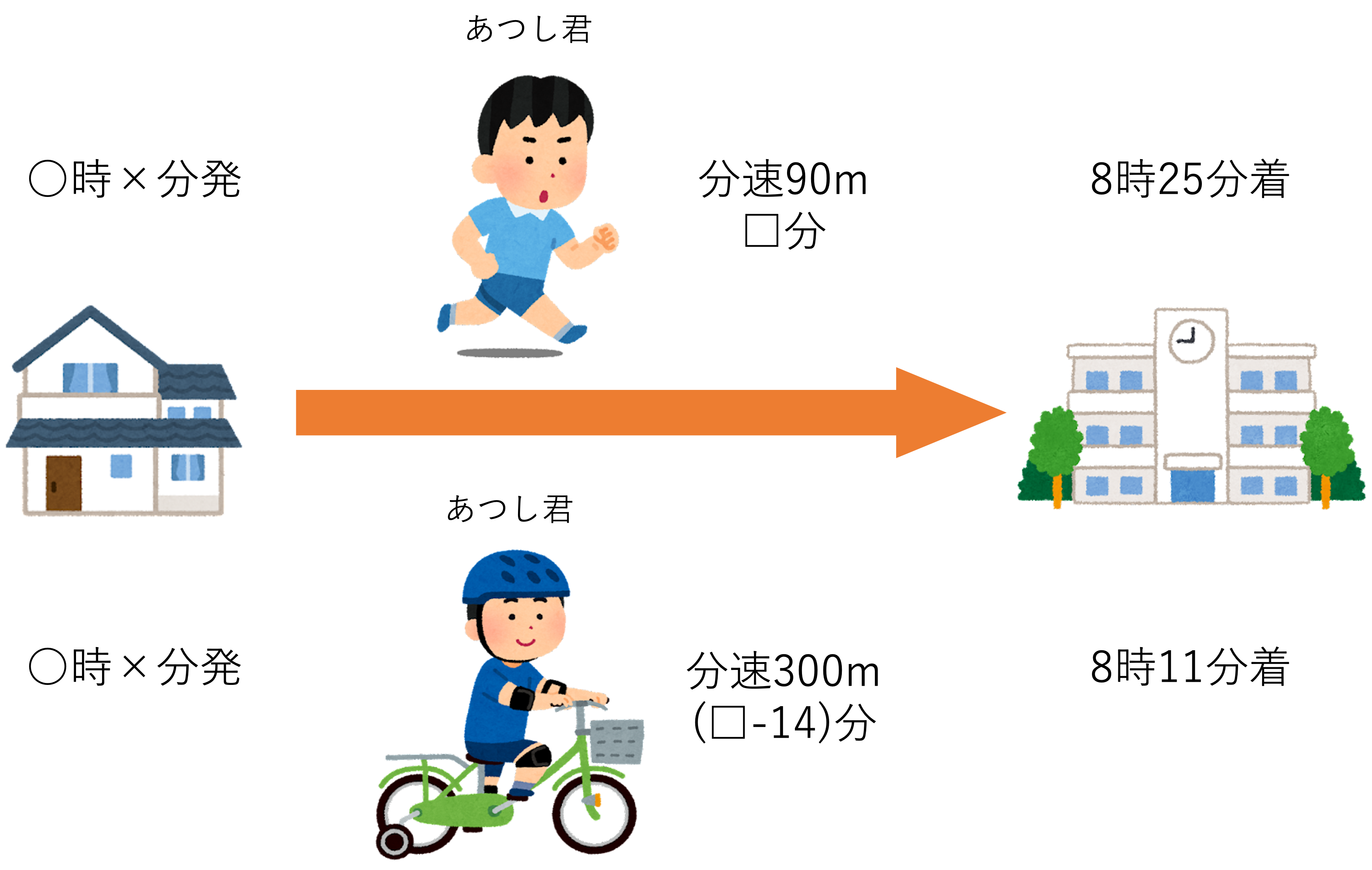
さて,ここまでで□を用いてあつし君が登校するときの時間と速さを表すことができましたが,ここで発展編で確認した比の関係を思い出しましょう。
道のりが一定である文章題では,速さの比と時間の比は反対になりましたね。今回の速さの比は,歩いた場合が分速90m,自転車に乗った場合が分速300mだったので90:300=3:10だと言えます。
他方時間の比は,歩いた場合が□分,自転車に乗った場合が(□-14)分だったため,□:□-14だと言えます。そしてこれらの比が反対になるということは,2つの比は次のように結び付けられ,□の中身を以下のように計算することができるのです。
3:10=□-14:□
3×□=10×(□-14)
3×□=10×□-140
7×□=140
□=20
このことから,あつし君は歩いた場合登校に20分かかることが求められました。今回の問題では歩いた場合学校に8時25分に到着すると言われているので,答えとなる出発時刻は8時15分の20分前,つまり8時5分だと分かります。
比の関係を覚えておくと,このように計算を簡単にすることができるので,ぜひ普段の演習から意識してみるといいでしょう。
A.8時5分
問題①の別解
なお1問目ということで比の関係を使わないで解く方法,つまり2つの計算式を立てて解く方法もご紹介しておきましょう。あつし君の家から学校までの道のりは分かりませんが,歩いた場合と自転車に乗った場合とで次のような2つの式が立てられますね。
【徒歩】家から学校までの道のり=90×□
【自転車】家から学校までの道のり=300×(□-14)
そして今回道のりの大きさが同じであることから,計算式は次のようにつなげることができ,□の中身を順番に求めていくことでも歩いた場合に20分かかることが求められるのです。
90×□=300×(□-14)
90×□=300×□-4200
210×□=4200
□=20
このようにやや遠回りではありますが,計算式を2つ作ることでも問題なく答えをみちにくことができますので,反対の比だっけ?同じ比だっけ?と悩んでしまった場合には基本の攻略法を使っていくといいでしょう。
問題② 単位の変換に気をつけよう!
続いてはやや難易度が上がります。タイトルでも書きましたが,今回の問題では単位の変換が必要となってきますので,そのことを忘れないようにしながら解き進めていただけると幸いです。
A君とB君の2人は,1周1.2kmの周回コースの休憩所にいます。この休憩所をA君は1分間に60mの速さで,B君は1時間に7.2kmの速さで同じ方向に出発して1周します。次の各問いに答えなさい。
(1)A君の速さは,時速何kmですか。
(2)B君は,A君が出発した何分後に出発すれば,ちょうど1周した休憩所で追いつきますか。
(足立学園中学校(2018)),一部改題
解説②
それでは(1)から順番に進めていきましょう。(1)はA君の速さを時速で表そうという問題でした。そのため発展編でお教えした内容は使わないものの,この手の単位に関する問題は計算ミスが起こりがちなので,気をつけて解いていきましょう。
今回A君は1分間に60m進む,つまり分速60mで進むことが示されていますね。この分速60mという値を時速〇〇kmという形に直すためには,まずは1時間あたりに何m進むかを計算し,その値を割り算してkmに単位を揃えていくのがいいでしょう。
いま1分間に60m進むとき,1時間=60分に進む距離はその60倍であることが分かるので,分速60mは時速60×60=3600mに変換できます。そして1km=1000mであることから3600mは3.6kmを指すことも分かるので,(1)の答えは時速3.6kmとなります。
なおこのとき,B君の時速が7.2kmであることから,A君はB君の半分のペースで走っているということも分かりますね。(1)の答えと直接関連してくるわけではないですが,思考を様々な方向に飛ばしながら計算を進めていくと(2)が解きやすくなるので,余裕がある場合には答えが次の問題とどう関わりそうかを考えてくといいでしょう。
A.(1)時速3.6km
続いて(2)の問題に移ります。この問題では,A君がB君の何分後に出発すれば同じタイミングで1周を走り終えられるか,が問われていますね。
そもそも前提として,A君の走る速さが時速3.6kmでありB君の走る速さが時速7.2kmであることから,同時に出発すればB君の方が早くゴールに着きます。そのためB君がA君より何分早くゴールするかを考え,その分だけB君が遅くスタートすればぴったり到着できる,と考えていきます。
そして今回の問題ではA君とB君が同じ1.2kmのコースを走ると設定されているため,2人が走る道のりが一定であることが分かりますね。ここまでの情報を整理できたら,あとは情報を図にまとめていきましょう。
道のりが一定であるため,基本の形は先ほどと同じような1本の線分図にまとめていけばいいのですが,今回の問題でも文中で大きさが明らかにされていない要素がありました。それが,A君が走るのにかかる時間とB君が走るのにかかる時間です。今回はこれらの要素をそれぞれ○分・□分として図を作っていきましょう。

このように整理すると,A君に関してもB君に関しても走る道のりと速さが分かっているため,道のり=速さ×時間の式に基づくとかかる時間が求められそうだ,と予想ができますね。
そのためここからは攻略法通り2つの式を作ることを目指していきましょう。ただし,今回の問題では式を作る過程で若干計算に工夫ができます。その工夫の仕方を覚えるように読み進めていただけると幸いです。
まずA君に関してですが,(1)の答えである時速3.6kmを使いながら計算をすると,かかった時間は次のようになります。単位の変換に注意しながら進めていきましょう。
道のり=速さ×時間
1.2km=分速60m×□分
1.2km=時速3.6km×□時間
\( □= \frac{1}{3} 時間=60× \frac{1}{3} 分=20分 \)
したがってA君は1周を終えるまで20分かかることが分かります。そのため後はB君が1周にかかる時間さえ求められれば,答えとなるハンデの時間も求められそうです。
ここで攻略法に則ると,このあとはB君の道のり・速さ・時間を2つ目の式にまとめないといけないのですが,道のりが一定のときの時間と速さの比の関係を思い出してみましょう。
A君とB君は走る道のりが同じなので,その速さの比と時間の比は反対になりますね。いま速さの比は時速3.6km:時速7.2km ,時間の比は20分:○分なので,次のように立式して○の中身に当てはまる数を算出することができます。
時速3.6km:時速7.2km=○分:20分
1:2=○分:20分
○分=10分
このことからB君は1周に10分しかかからないことが分かります。1問目と同様この問題でも速さと比の関係を覚えておくと計算が簡単になります。ぜひ参考にしてみてください。
そしてA君が1周に20分,B君が1周に10分かかるということは,B君が20-10=10分遅れてスタートすれば同じタイミングで走り終わることができそうです。最後に単位に注意すると,答えは10分後となります。
A.(2)10分後
問題③ 情報の整理で気を抜かないようにしよう!
それでは最後の問題に移ります。言うまでもなくこの問題でも速さと比に関する情報が出てきますが,今回は明らかになっている数値が少なめです。
そのため回答を導くのに苦戦するかもしれませんが,基礎的な解き方を抑えていれば問題ありません。基本に忠実に進めていきましょう。
沙保里さんが3.2km離れた場所へ向かって歩きはじめました。4分の1だけ進んだところから速さを5分の1だけ減らしたら,予定より10分遅れてつきました。このとき,次の各問いに答えなさい。
(1)速さを減らしたあとは,速さを減らす前と比べて同じ距離を進むのにかかる時間は何倍になりますか。
(2)速さを減らしてから何分で着きましたか。
(3)はじめの速さは時速何kmですか。
(埼玉平成中学校(2017),一部改題)
解説③
今回の問題では,沙保里さんの速さが途中で変化するという上2つの問題と異なるシチュエーションが設定されています。そのため道のり・速さ・時間のどこが一定なのかが分かりづらく,なかなか難易度が高かったのではないでしょうか。
速さと比の問題の中にはこのように,どの部分が一定なのか分かりづらい問題も存在します。そのような場合は設問を機械的に一つずつ解くことをオススメします。
というのも,初めの方の問題は余り深く考えないでも解けるものが多いからです。また設問の答えを使いながら問題を進めていく必要があるから,という理由もあります。今回のような問題であれば,とりあえずは速さを減らす前と後とを比べていき,その後全体を捉えていくといいでしょう。
さて(1)ですが,この問題では速さを変える前と後とで同じ距離を進むのにかかる距離が問われていますね。
この文章では道のりが一定のときという仮定がなされているので,先ほどから使っているような比の関係を使えば答えられそうです。問題で沙保里さんは速さを5分の1だけ減らす,つまり5分の4にしたということが示されています。
そのため速さの比は1:\(\frac{4}{5}\)だと言えますね。そして速さの比が1:\(\frac{4}{5}\)のとき時間の比はその反対になるため,同じ道のりを進むのにかかる時間は\(\frac{4}{5}\):1の関係に,つまり\(\frac{4}{5}\)倍になります。
このように問題の全容が見えていなくても比の関係さえ分かれば答えを導くことができるので,ぜひ比の関係は頭に入れておきましょう。
A.(1)\(\frac{4}{5}\)倍
続いて(2)に移りましょう。この問題では速さを減らしてから到着するまでにかかった時間が問われています。なかなかどこから手をつけていけばいいのか分かりにくいですが,かといって(1)のように頭の中だけで完結しそうにもありません。
このような場合には一度図を書いて中身を整理してみましょう。線分図を書く上で注目したい要素が10分遅れたという言葉です。この10分の遅れというのは速さを減らしたせいで生じたものですよね。
そのため最初の4分の1を歩き終えてから到着までにかかるはずだった予定を□分,4分の1を歩き終えて速さを低くしてから到着までにかかった実際の時間を□+10分として,図を作っていきましょう。加えて沙保里さんの元々の進む速さを時速○kmとすると,下のような線分図が書けるはずです。
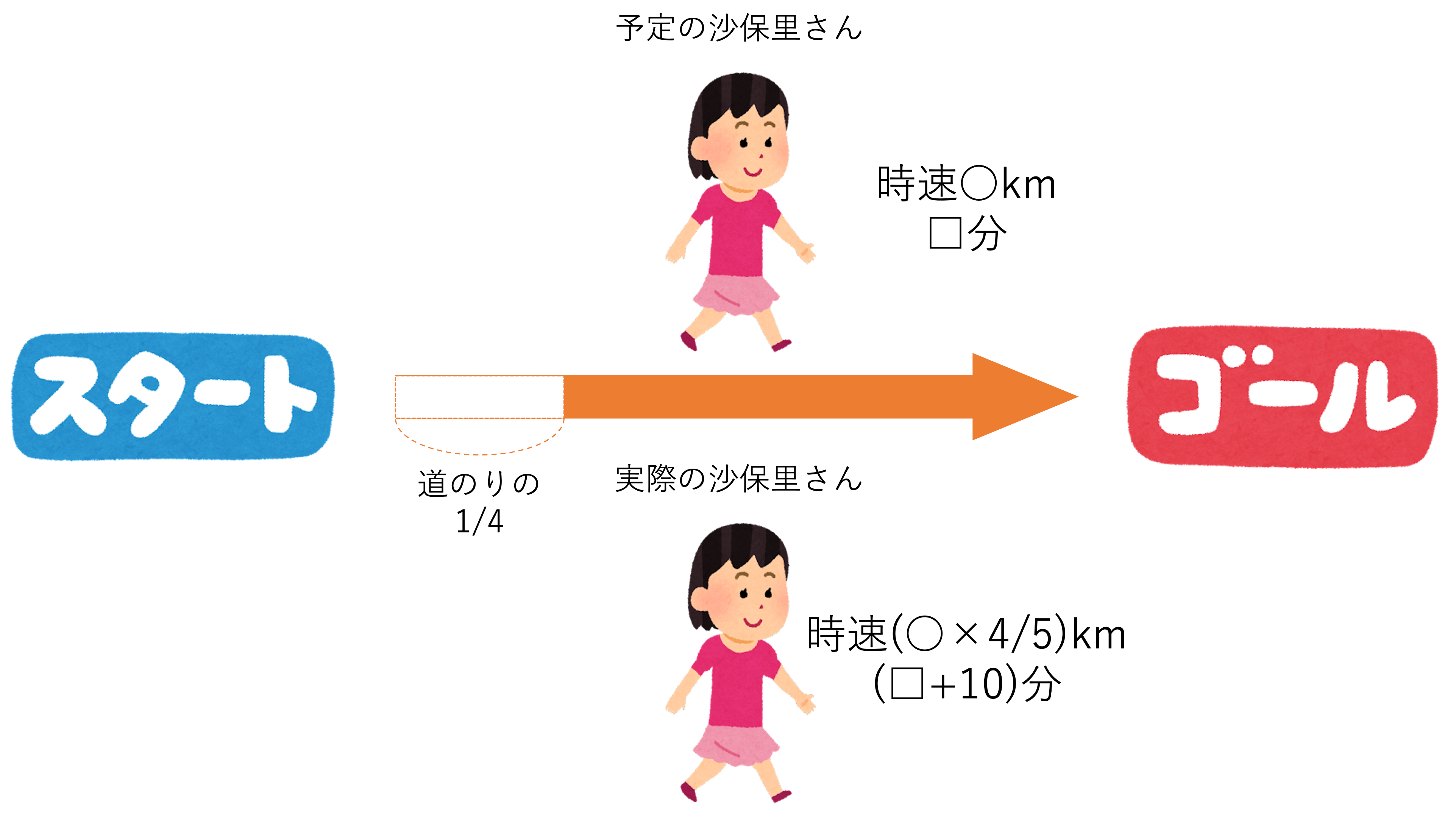
そしてこの図と先ほどから使用している道のりが一定であるときの速さと時間の比が逆になるという関係を用いると,次のような式を作ることができます。
○:\(\frac{4}{5}\)×○=□+10:□
1:\(\frac{4}{5}\)=□+10:□
4×(□+10)=5×□
□=40
このことから当初は最初の4分の1を進んでから40分後に到着する予定だったことが求められました。そしてその予定より10分間遅れてしまったということから,答えは50分となります。
以上のように比に注目すると問題が解きやすくなります。また(2)では10分遅れという言葉に注目することも重要でしたね。文章題では全ての情報をあり余すことなく使わないといけないので,まだ使っていない数字はどれかと探していくのも良い攻略法でしょう。
A.(2)50分
それでは(3)の解説でこの記事を締めくくります。この問題では沙保里さんが初めに歩いていた速さの計算をする必要があります。
ここで(2)に一度立ち返ると,(2)の問題は歩き始めてから道のりの4分の1を過ぎたところで速さが変わらなかったという予定の場合と速さが変わってしまったという実際の場合とを比べながら線分図を作っていきました。
ここで予定の場合の速さである分速○mとは,つまり4分の1を過ぎるまでの進む速さを指すので,今回は上の線分図を見ながら○の中身を計算できれば答えが求まりそうです。
この手の文章問題の終わりの設問は,それまでに求めた答えや考え方を使うケースがほとんどですので,一から考えていくのではなくここまでの答えをどう活かすか考えていくのも有効だと言えます。
さて,それでは先ほど求めた□の中身を埋めたりしながら,沙保里さんが出発してからゴールするまでの予定の場合の様子を線分図に書き直してみましょう。
なお,ここで答えが明らかになるのは□の中身だけではありません。問題文に登場する3.2kmという道のりの値も使えば,何km地点で速さを落としたのかといったことも分かりますね。このように徐々に情報を更新していくと,次のような図を作ることができます。

この図から,道のりの4分の1である0.8kmを過ぎたところで,沙保里さんは当初残りの2.4kmを時速○kmで40分間歩いて目的地まで到着する予定だったということが分かります。
したがって,この関係を速さ=道のり÷時間の関係に当てはめると予定の沙保里さんが進む速さが計算できそうです。それぞれの値を当てはめて速さの値を計算すると,答えは次のようになります。このとき単位の変換に気をつけていきましょう。
沙保里さんの速さ=2.4km÷40分=分速0.06km
分速0.06km=時速0.06×60km=時速3.6km
A.(3)時速3.6km
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。
終わりに
今回の記事では,速さと比に関する文章題を解説していくシリーズの第三弾として,実際に受験で出題された問題を引用しながら応用的な問題の解き方を説明していくものでした。
速さと比という単元は,どんな難易度の受験問題でも必ずと言っていいほど登場してきます。そのためおすすめ記事や参考書籍を使いながら,知識の定着に励んでいきましょう。本記事が今後の学習のお役に立てば幸いです。