本記事では速さと比に関する問題を解説するシリーズの発展編として,例題を使いながら問題の攻略法をご紹介していきます。この速さと比という単元は,受験に登場する多くの文章題の中でも取り組みにくいものです。そのため早いうちから対策しておくことが必須となります。発展編と称しつつも,内容自体は低学年・中学年の方でも分かりやすいようにしていますので,是非一読ください。
Contents
基礎編の振り返り!速さと比の計算とは?
まずは前回の記事の冒頭で確認した速さと比の計算とは何か,ということを再度確認しておきましょう。端的に言ってしまえば,速さと比の計算とは道のり・時間・速さが関係する文章題のことと指します。ただしそれだけが重要なのではなく,ある1つの要素が全く同じになっていて,それ以外の要素については2種類の数値が与えられるということも重要です。この点については攻略法の紹介の章で詳しく説明します。
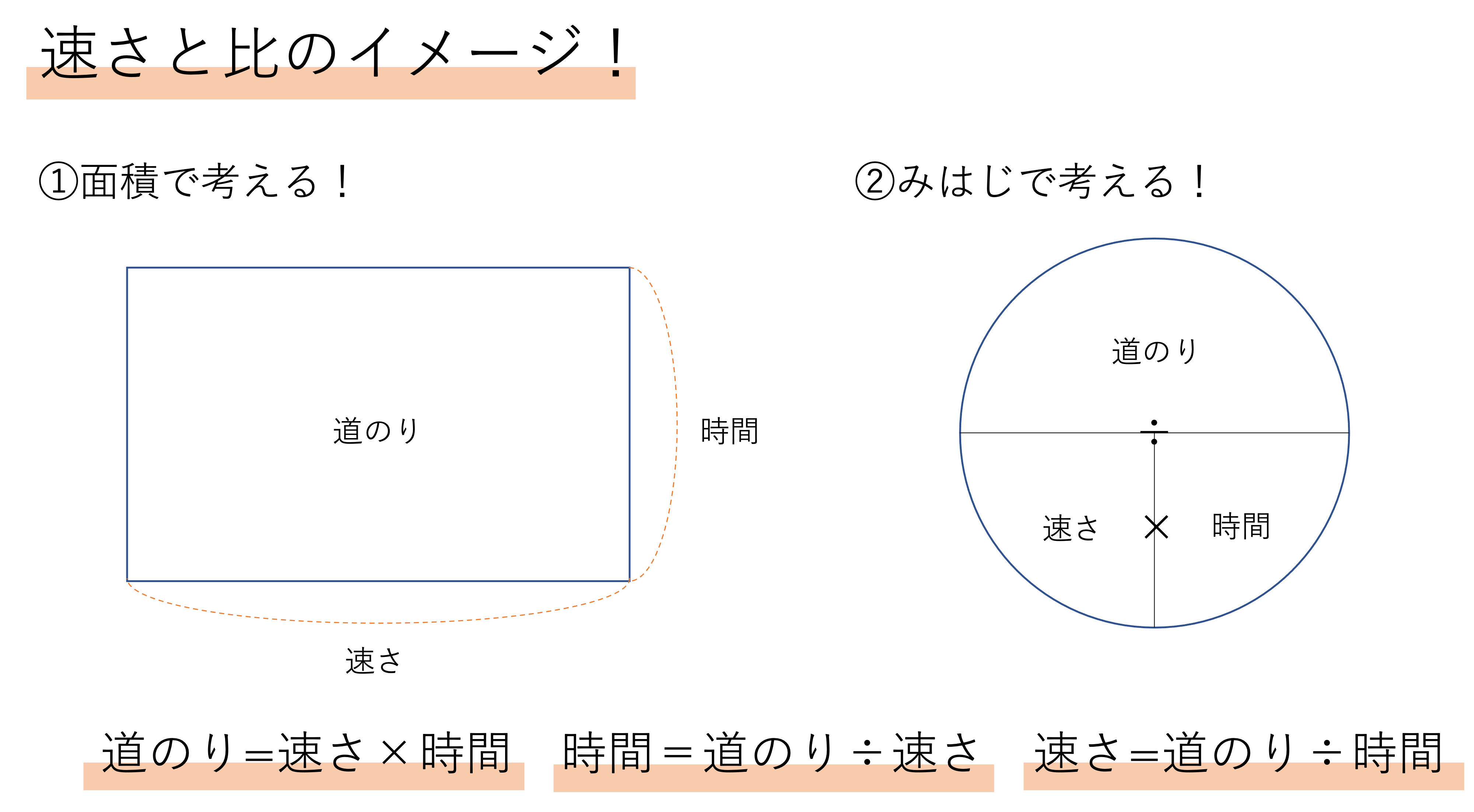
前回の記事ではこの速さと比の計算を解いていく上で必ず知っておかねばならない,道のり・時間・速さの意味や計算方法についてご紹介していきました。これらの計算に関する公式覚えるためのコツとして面積の計算と結びつけたり,「みはじ」の図を持ち出したりもしましたね。考え方や覚え方は基礎編の記事をご覧いただくとして,問題を解くにあたってしっかり頭に入れておきたい公式についてはもう一度確認しておきましょう。
① 速さ=道のり÷時間
② 道のり=速さ×時間
③ 時間=道のり÷速さ
速さと比の基本構造!
ここからは例題を使いながら速さと比という文章題の基本構造について学んでいきましょう。まず全ての問題に共通する特徴が,速さ・道のり・時間の3つが登場するということ,そしてその中に一定になっている要素が存在するということです。そしてどの要素が一定になっているかで,線分図の解き方や注意するポイントが若干変わってきます。一定とはどういうことか,というのは各パターンの解説で詳しく説明していますが,まずは速さと比に関する問題と出会ったら,一定となっている要素は速さ・道のり・時間のうちのどれかを考えていくといいでしょう。
パターン① 道のりが一定の文章題!
それではまずは道のりが一定となっている問題を見ていきます。下に挙げているのは道のりが一定になる問題の例題です。この問題を使いながら,攻略法を説明していきます。
学校から公園まで行くのに,Aくんは10分,Bくんは20分かかります。Aくんが分速50mで歩くとき,Bくんが歩く速さを求めなさい。
このような文章題に出会ったら,まずは中身を整理していくことが重要です。今回は道のりが一定だと示されていますが,受験で出てくる問題では何が一定になっているかを自分で読み取る必要があるため,まずは答えや計算方法を考える前に中身をまとめることを意識していきましょう。今回の問題ではAくんとBくんという2人の子どもが登場し,この2人が歩くというシチュエーションが想定されています。2人が歩くので,それぞれペースやかかる時間は異なってくるのですが,AくんもBくんも学校から公園までを歩くことは共通していますよね。このようにどこからどこまでの区間を動くのかという条件が一致しているとき,道のりが一定であるといいます。どの部分が一定であるかを判断するには慣れが必要なので最初のうちはとまどうかもしれませんが,道のりが一定である場合は〇〇から□□へ,という言葉が含まれていることが多いので,そのような語句に注目してみるといいでしょう。
さて,一定である部分を確認できたところで,今度はAくんとBくんが歩くときに道のり・速さ・時間を図にまとめていきましょう。文章題の中身を頭の中で整理できたとしても,図におこさないままでは計算を間違えてしまいやすいです。それゆえ図表の作成は重要になってきます。今回はBくんが歩く速さを問われているので,その部分を分速□mとして図にまとめていきましょう。
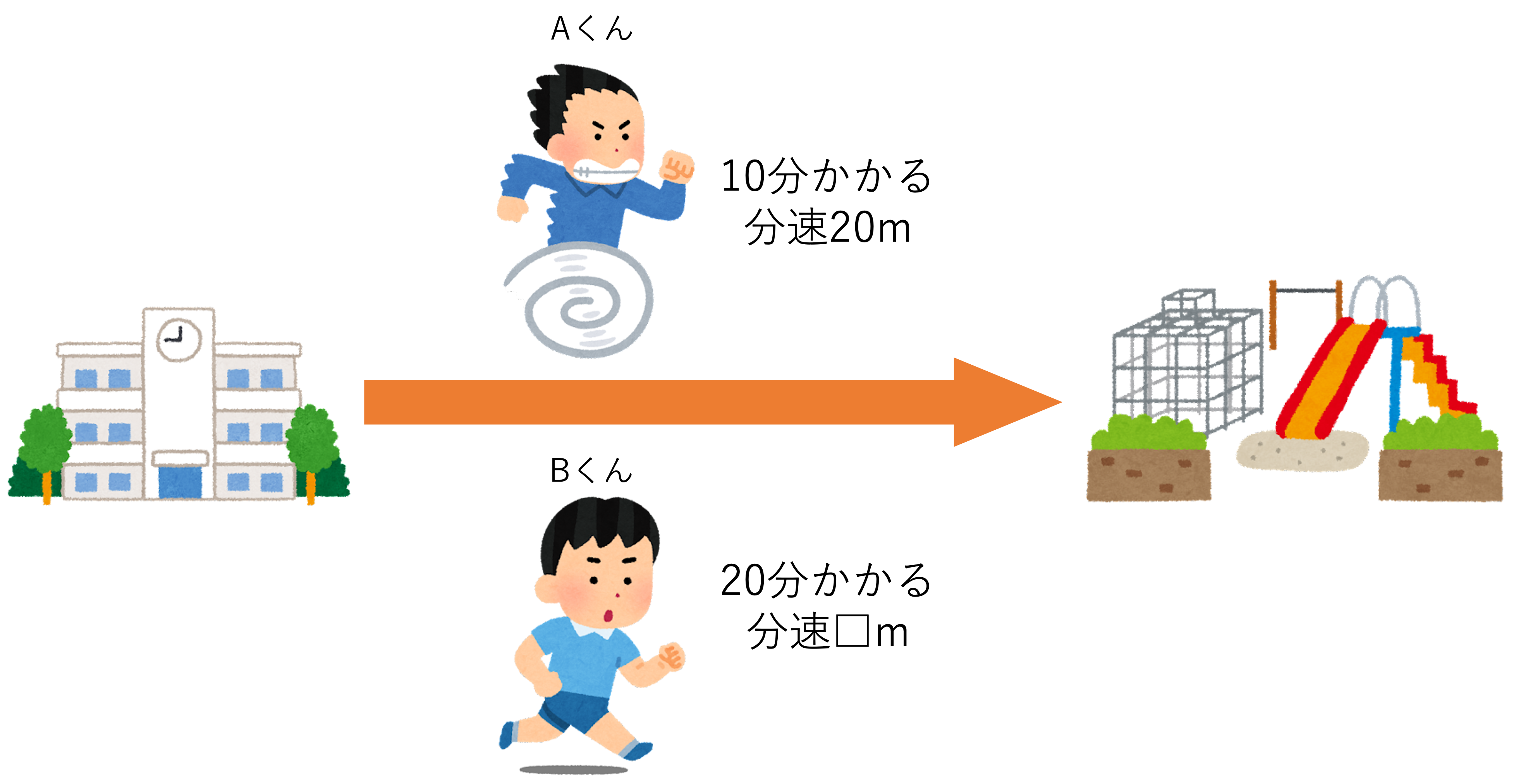
今回は1問目ということでポップな図を用意しましたが,ここまで丁寧に書かなくても問題ありません。大切なことは1本の線分を学校から公園までの距離,つまりはAくんとBくんが進む道のりとみなし,その上下にそれぞれの速さや時間をまとめていくということです。線分図の書き方は他の記事でも紹介されていますが,速さと比の計算でも線分図は有効に使えます。ぜひ覚えておいてください。
ここまで情報が整理できたら,次は2通りの計算式を作るという作業に移りましょう。2通りというのは,今回の問題だとAくんに関する式とBくんに関する式になりますが,問題によっては行きと帰りだったり昨日と今日だったりします。ともかく,速さと比の計算では道のり・速さ・時間に関する2つの式が作り出せるはずなので,それらの式を考えていきましょう。このとき分からない部分は○や△を使って置き換えたり道のり・速さといった単語をそのまま使ったりしながら,全体像を捉えるように式を作ってあげることがポイントです。まずAくんについてですが,Aくんは分速20mで歩くと10分で学校から公園までたどり着くことができました。これを道のり=速さ×時間の式に当てはめると,次のように整理できますね。
学校から公園までの道のり=分速20m×10分
ここで分速20mという速さの値は,1分という単位時間ごとに20m進むことを指すのだったと思い出しましょう。この速さを変えずに10分間歩くと,その間に20×10=200m進むことになりますね。これにより上の式はより簡潔にまとめられます。
学校から公園までの道のり=分速20m×10分=200m
この式により今回の問題の道のりが200mであることが明らかになるのですが,ここで一旦Bくんの式を考えていきましょう。慣れてきたらこの200mという値をそのまま使って計算していくこともできるのですが,初めのうちはミスを防ぐために慎重に進めていくことをオススメします。さて,Bくんは分速□mで歩くと20分で学校から公園までたどり着けると示されていました。このことからAくんと同じように式を立てると,それぞれの要素の関係は次のように整理できます。
学校から公園までの道のり=分速□m×20分=□×20m
このように2つの式を立てると,Aくんの式とBくんの式が繋がりそうだなと判断できますね。というのもこれらはどちらも歩いた道のりに関して立てた式であり,上で確認したように今回の問題で2人が歩いた道のりは同じだったため,次のように式同士が繋がるというわけです。
200m=学校から公園までの道のり=□×20m
200m=□×20m
以上のように立てた2つの式のつながりを見つけるということが速さと比の計算では大事になってきます。そして上の式を□について解くと,答えは10分になります。速さと比に関する問題のほとんどはこの道のりが一定となっているパターンで出題されるので,この攻略法をまずはしっかり自分のものにすることを意識しながら,問題集や参考書を進めていくことをオススメします。
A.分速10m
ちなみに今回の問題では,Aくんは分速20mで10分・Bくんが分速10mで20分となんらかの関係がありそうな答えが導かれました。実はこれは偶然ではなく,道のりが一定の問題では速さの比と時間の比は逆になります。この関係を逆比というのですが,つまりAくんとBくんの歩く時間が20:10-=2:1のとき,速さの比はその逆である1:2になるというわけです。この関係は理解していなくても問題ありませんが,知っていると解答がスムーズになるのでぜひ覚えておきたいところです。
パターン② 時間が一定の文章題!
続いては時間が一定になる文章題です。一定の指すところは1問目と変わりませんが,どの部分が違うのかを考えながら読んでいただけますと幸いです。
今日Aくんは10分間走で1000m走りました。翌日ペースを1.5倍にして走るとき,Aくんは何m走ることができるか求めなさい。
それでは1問目と同様,まずは中身を整理していくことから始めていきましょう。今回の問題は時間が一定な文章題の例題として登場させましたが,この問題ではAくんが10分間走をするという場面が想定されています。文章を見ると「今日」「翌日」という単語が見られるため,どうやらAくんは習慣的に10分間走をしていることが読み取られますが,この10分というのはAくんが走っている間の時間のことですよね。そのためこの問題では,今日と明日とでAくんが走る時間が共通しているというわけです。このように動き始めから動き終わりまでの間隔が共通している場合,時間が一定であると言えます。
そしてこのように問題をながめてどの部分が一定であるか判断できたところで,次は図にまとめるという作業に移りましょう。今回は,今日Aくんが走った速さを分速□m・翌日のAくんが走った道のりを○mとして表を作っていきます。分からないところが1問目に比べると多めですが,ひとまず分かるか分からないかに関係なく図に書き起こしてしまうことがポイントです。図に起こす段階では答えの求め方・計算方法は念頭に置かず,頭の中にある情報をまとめることだけを意識していきましょう。なお今回は1問目のように1つの線分の上と下に情報をまとめることはできません。それは道のりが一定ではないからです。このように道のりが一定でない問題では,1本の線分でまとめる代わりに,線分を2本用意して図を作ってあげるといいでしょう。
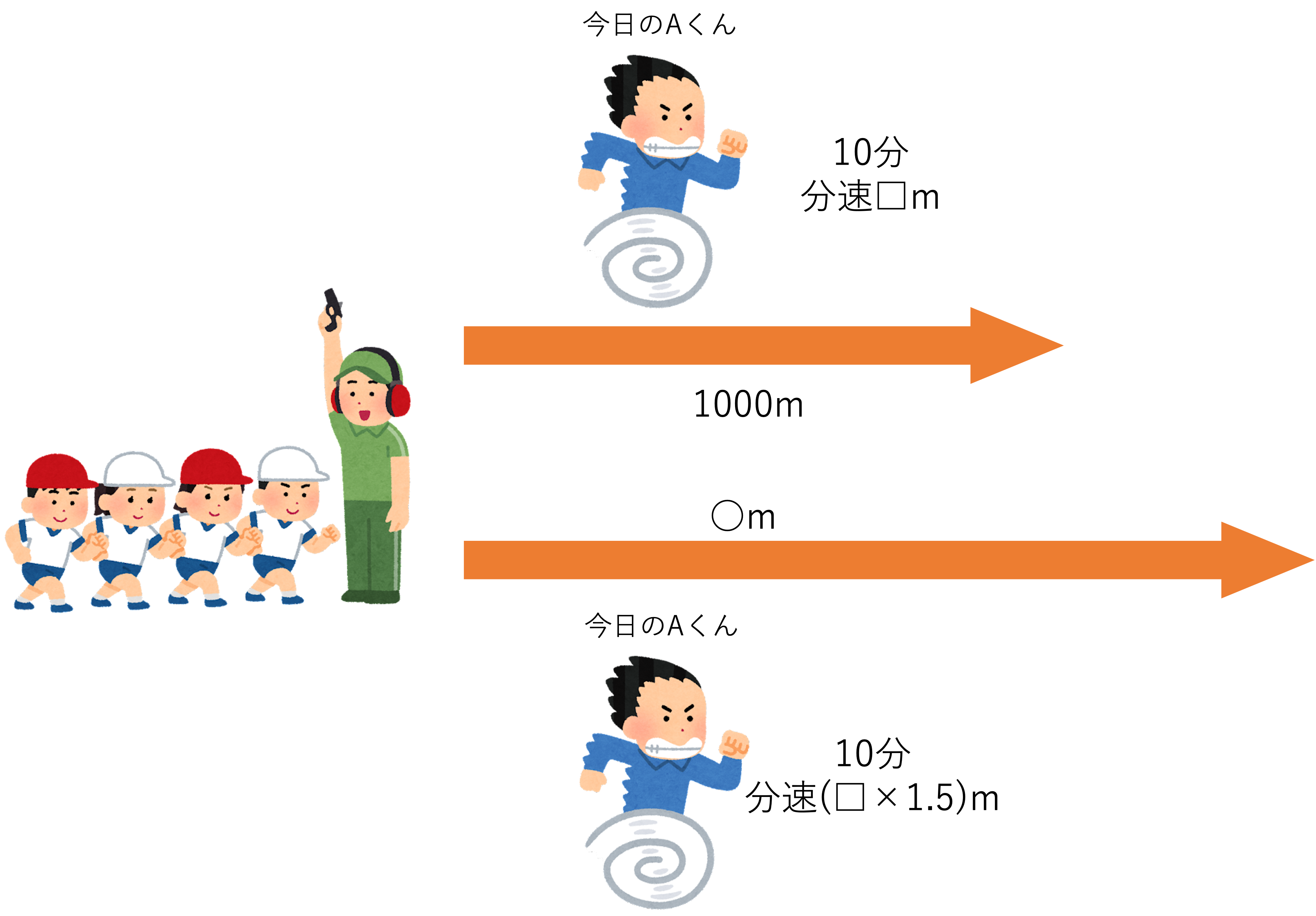
そして次は2通りの計算式を作るというステップに移りましょう。今回の2つの式とは言うまでもなく今日のAくんに関する式と翌日のAくんに関する式のことですね。まず前者の今日のAくんに関する式ですが,上の表を見るとその内容は次のようにまとめられます。
1000m=分速□m×10分
ここでこの式において,Aくんは10分間で1000m走ったということは,同じペースで走り続けるという速さと比に関する問題の前提に基づくと,1分あたりに100m走ったことになりますね。そのことは速さ=道のり÷時間という公式からも明らかです。そのため今日のAくんに関する式は次のように更新できます。
1000m=分速100m×10分
次に翌日のAくんに関する式を立てていきましょう。翌日のAくんは,10分間で○m走ったとされていました。そしてペース,つまりは速さが今日の1.5倍になったということから,次のような式を作ることができると分かります。
○m=(分速□m×1.5)×10分
そして2つの式のつながりを探していくと,答えとなる翌日のAくんが走った距離を求めるためには今日のAくんの走った速さの値が必要であり,その値を求めるためには今日のAくんに関する式が有効だと言うことがわかります。今回は立式の段階で,今日のAくんは分速100mで進んでいることが計算できたので,その値を当てはめると次のように答えを求めることができます。
○m=(分速100m×1.5)×10分=150×10m=1500m
A.1500m
以上のように内容をまとめる→図に起こす→2つの式を作る→比べるという作業を経ることで,速さと比の問題の答えは簡単に求めることができます。参考にしてみてください。なお速さと比の関係をここでもご紹介しておくと,今日のAくんは分速100mで1000m・翌日のAくんは分速150mで1500mとどちらの値も1.5倍になっている,つまり1:1.5の関係になっていることが分かりますね。このように時間が一定のとき,道のりの比と速さの比は同じになります。先ほどの場合の逆比との違いを明確にしながら,頭に入れておくといいでしょう。
パターン③ 速さが一定の文章題!
最後にご紹介するのは速さが一定である文章題です。ここまで道のり・時間が一定である文章題を扱ってきたので,何となくの要領は掴めた頃かと思われます。一度ここまで習ったことを振り返りながら問題にチャレンジしてみてもいいかもしれません。
A君は決まった速度で自転車を漕ぎます。2分で800m進むとき,2時間では何km進むことができるか求めなさい。
さて,まずはこれまで通り内容の整理から進めていきましょう。今回は速さが一定とのことですが,このことは「決まった速度で」という一文から読み取れますね。そのため今回の問題では,Aくんが自転車を漕ぐスピードが変わらないということが分かります。このように動きの場合が違ってもスピードが変わらないとき,速さが一定であると言います。ここまで明らかに示されていることは比較的少ないでしょうが,それでも道のり・時間のパターンと同様に,何らかの単語から一定であることがわかるはずです。その部分を意識しながら,問題の内容を整理するという手順を進めていただけますと幸いです。
そして内容がなんとなく頭の中でまとまったら,次は図に中身を整理すると言うステップに移りましょう。今回の問題では進む道のりの大きさが違うので,2つの線分を使いながら図を作っていくといいでしょう。Aくんが自転車を漕ぐ速さを分速□m・2時間で進んだ距離を◯mとすると,次のような図が完成します。
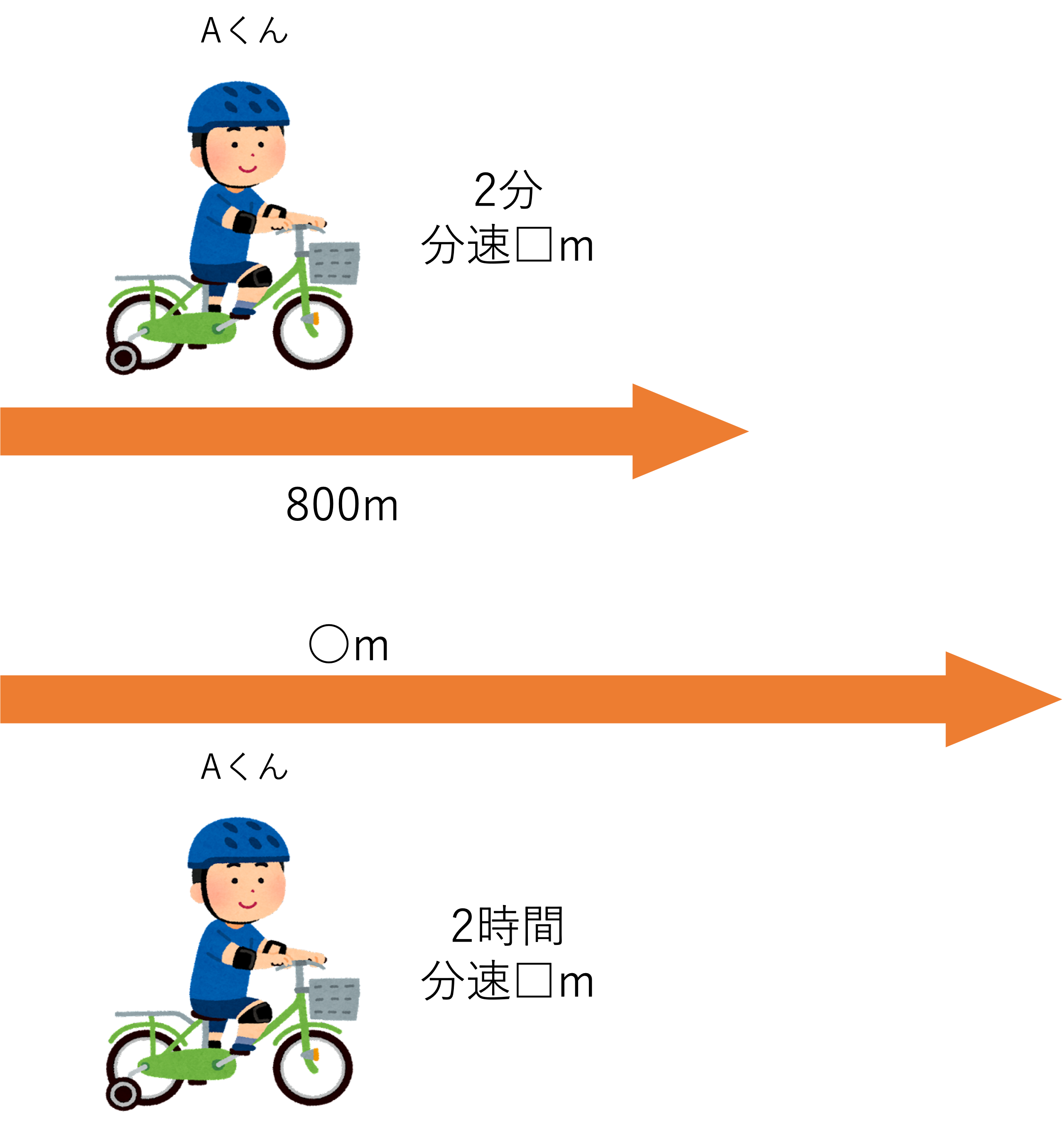
ここまで図を作ることができたら,次は2通りの計算式を作っていきましょう。今回の2通りの式とは,2分走ったときのAくんに関する式と2時間走ったときのA君に関する式になりますね。まず前者ですが,分速□m・2分間で800m走ったため次のような式が成立します。なお,これまでは道のり=時間×速さの公式に基づいて立式していましたが,今回は速さ=道のり×時間の公式を使って式を作っていきます。このように慣れてきたらどの公式を使うか選択し,計算を早く簡単にしていくことを狙ってみてもいいでしょう。
分速□m=800m÷2分=分速400m
次に2時間走ったときのAくんの式を立てていきましょう。Aくんの進む速さが分速□m・道のりが○mだったため,次のような式が作れます。なお今回の時間の単位は2「時間」であるため,一度単位を分に直す必要があります。そのことに注意して計算を進めましょう。
○m=分速□m×2時間=分速□m×2×60分=分速□m×120
そしてこれら2つの式を比べると,上の式で求めたAくんの速さに関する値が下の式に当てはまりそうだ,そしてその値を使うと道のりが求められそうだ,という見当がつきますね。この見立てにしたがって□に400という数字を当てはめて計算を進めていくと,次のような答えが求められます。今回は答えである道のりをkmで表さなければいけないので,1km=1000mであることに気をつけて単位を直す作業も忘れないでくださいね。
○m=分速400m×120=48000m=48×1000m=48km
A.48km
このように,速さと比に関する問題ではときに単位の変換が求められます。この点が速さを比の問題を苦手としやすい原因の一つなのですが,たくさん問題を解くことでひっかからなくなります。本番まで演習を積んで,ケアレスミス対策もしていきましょう。
なお今回の問題では,Aくんが2分走るときは800m・2時間=120分走るときは48km=48000m進むことが分かりました。これらの値を比較するとどちらも60倍になっている,つまり1:60の関係になっていることが分かります。このように速さが一定のとき,道のりの比と時間の比は同じになります。上でご紹介した道のりが一定の場合・時間が一定の場合,と合わせて覚えておくといいでしょう。
まとめ
- 速さと比は①問題を整理する②図に情報を起こす③2つの式を立てる,のステップで攻略しよう!
- 道のりが一定のとき,速さの比と時間の比は逆になる!
- 時間が一定のとき,道のりの比と速さの比は同じになる!
- 速さが一定のとき,道のりの比と時間の比は同じになる!
終わりに
今回の記事では速さと比に関する問題を解説するシリーズの発展編として,問題の攻略法をご紹介していきました。基本的な解き方は以上になりますが,受験問題となるとまた解く際の手応えが変わってくるでしょう。次回の応用編では入試問題を引用しながら本番を見据えた攻略法をご紹介していきますので,よければご参照ください。本記事が今後の学習のお役に立てば幸いです。
(ライター:大舘)


















