倍数算というものをご存知でしょうか。倍数算とは中学受験に登場する文章題の中の1つを指します。つるかめ算などと比べるとあまり注目されることは少ないですが,中堅校はもちろん難関校でも出題されやすい問題ですので,対策が必須となります。今回は実際に登場した受験問題を引用しながらより詳しい攻略法をご紹介していきますので,まだあまり馴染みがない人は基礎編の記事を確認してみてください。
基礎編の振り返り!
それでは手始めに,前回ご紹介した「倍数算とは何か?」「倍数算はどうやって解けばいいの?」といった基本的な事項について復習していきましょう。倍数算とは,問題文に2通りの比が登場するような問題を指しました。具体的には,お金のやり取りというシチュエーションが想定されることが多いです。誰かと誰かの所持金の比が○:□で,モノを買ったりお小遣いをもらったりお金の受け渡しがあったりして所持金が変化すると,比が△:☆に変化した,というのがテッパンの出題形式になります。まずはこのような,問題を倍数算だと見分ける判断基準をきちんと覚えておきましょう。
そして前回の記事では,この倍数算を攻略する上で大切なテクニックとして,線分図という整理の仕方をご紹介しましたね。線分図とは何らかの状態を1本の線で表し,その線を区切ったり伸ばしたりすることで,色々なモノの数量の関係を比較する図のことを指します。
倍数算においては,先程申し上げたようにいくつかのモノの間でのやり取りや増減が発生します。そのため,一般的にはやりとりの前後の状態を2本の線分で比較するような図を作ることで攻略を狙います。
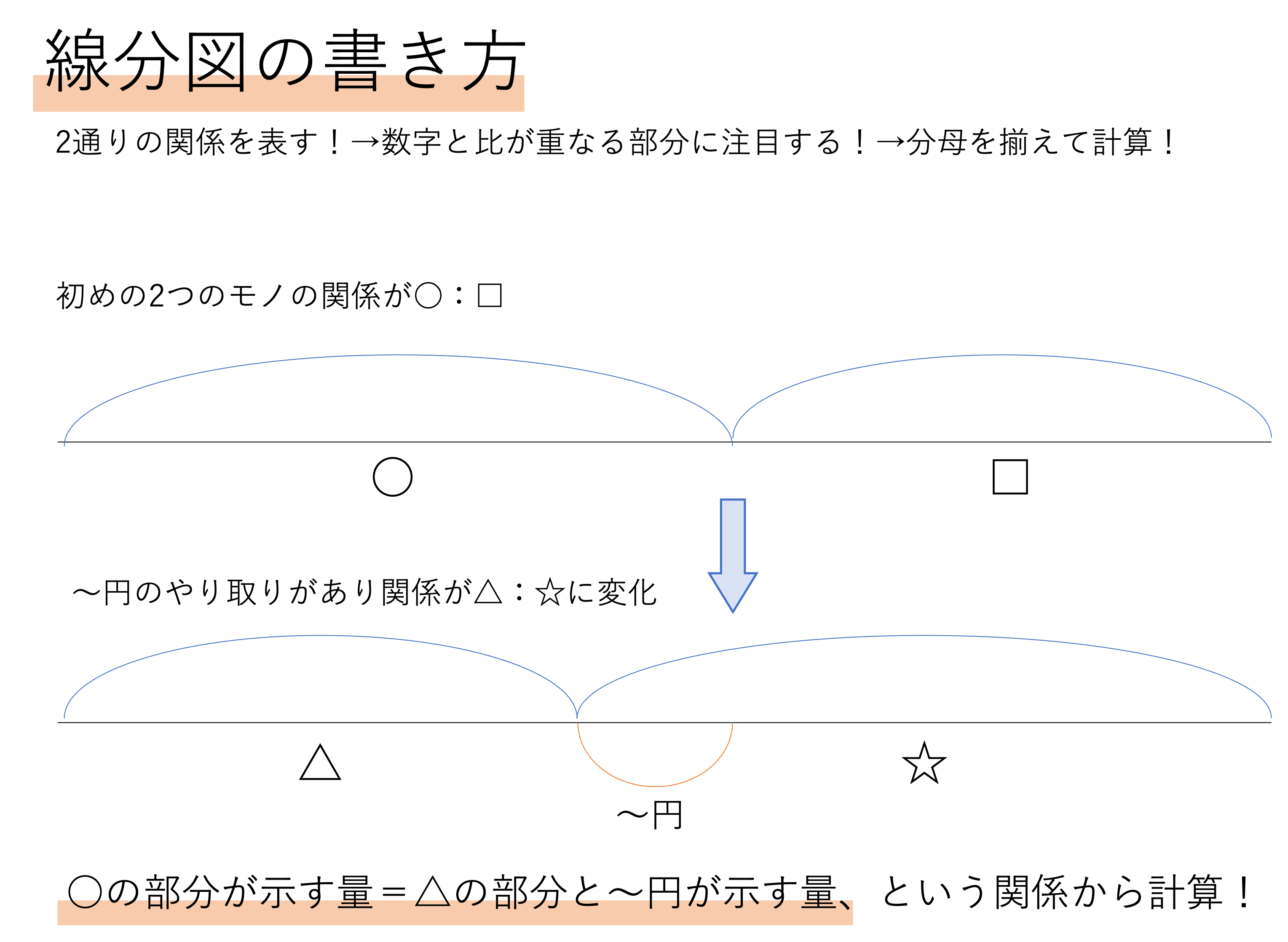
そして線分図を作った後に必要とされる計算として,比を揃えるという作業もご紹介しましたね。2つの比の内容が全く違う以上,初めの状態の比が示す「1」という値とやり取り後の状態の比が示す「1」という値は全く別物になるのです。そのため,同じ部分を指す比を最小公倍数で揃え,比を揃えた上で数値と割合・初めの比とやり取り後の比を照らし合わせなければいけません。全体の量が変わらない場合は全体に,片方の量が変わらない場合はその片方に注目して比を揃えてあげましょう。また後述しますが,同じ部分が全く存在しない問題に出会ったら,思い切って別の解き方を考えてみるのが吉です。
このようなことを前回の記事ではお伝えしていきました。まだイマイチ思い出せない・しっくり来ない人は,よろしければ【基礎編】の記事をご確認ください。
問題①
ここからは問題演習に移りましょう。といっても,倍数算ではそこまで難しい問題は登場しません。前回の基礎編と似たような問題が多いですが,一度読んだことがある問題が出てくる分,細かいミスに気をつけて計算してみてください。
AとBの所持金の比は3:4です。Bが1400円使うと,所持金の比は4:3になりました。Aの所持金はいくらですか。
(西武学園文理中学校(2015),一部改題)
解説①
この問題は,前回の記事の例題とほとんど同じような倍数算です。まずはウォーミングアップがてらに,構造がわかりやすい問題を引用しました。短い文章ながらも,所持金に関する2つの比があって,その間で「Bが1400円使う」というやり取りが発生しているという要素から,倍数算であることが判断しやすいですよね。
それでは,問題が倍数算であることが明らかになったところで,次は線分図に関係をまとめてみましょう。今回はBの所持金が減っていることに注意して,線分の長さを決めなければいけません。丁寧に線分図を作ると,次のように問題を整理できるかと思われます。
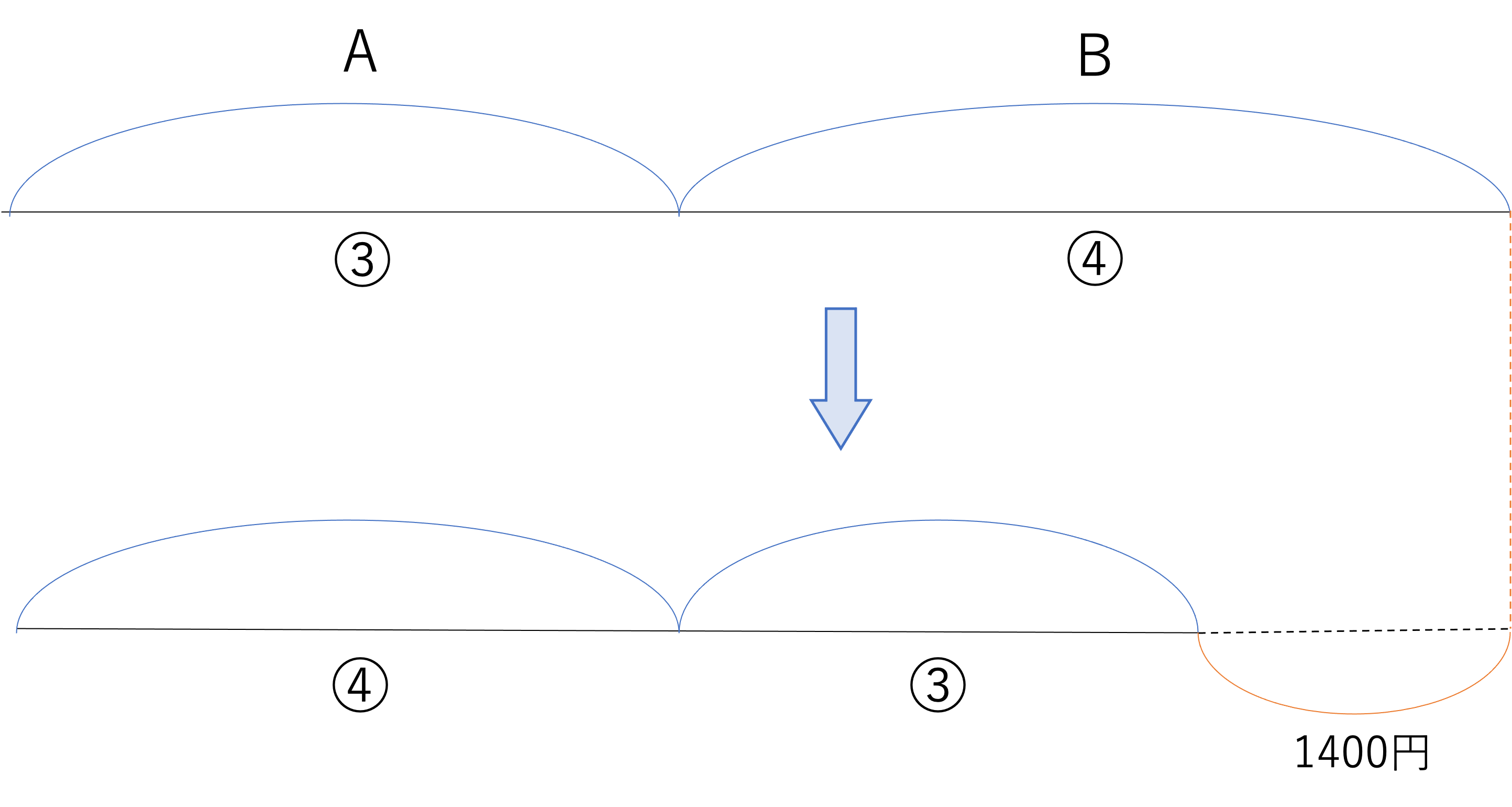
以上のように図をまとめると,今回の問題では「1400円」という数字に注目して計算を進めていけばよさそうだな,ということに気づけるのではないでしょうか。ただ,もし気づけなかったとしても,この後は分母を揃えるという手順を踏めばいいことは既に理解していただけているかなと思います。答えの計算方法にピンときていてもきていなくても,大事なのは手を動かすことです。手順通りに進めることを意識していきましょう。
さて,ここでお気づきの方もいると思うのですが,今回の問題ではどちらの比の分母も7になっています。そのため分母を揃える必要がないと思いがちかもしれませんが,実は今回は全体の比ではなく,Aの所持金に関する比を揃えてあげる必要があるのです。前回取り上げた例題では全体の所持金が変わらなかったので全体の量,つまり比の分母はこの問題では変わらないため,全体が7で揃っていようと意味がないのです。対してやりとりを通して変化のないAの比は3から4に変化しています。量が変わっていないのに比が増えているのはおかしな話ですよね。そのため,下の図のようにAの比を揃えてあげる,というわけです。
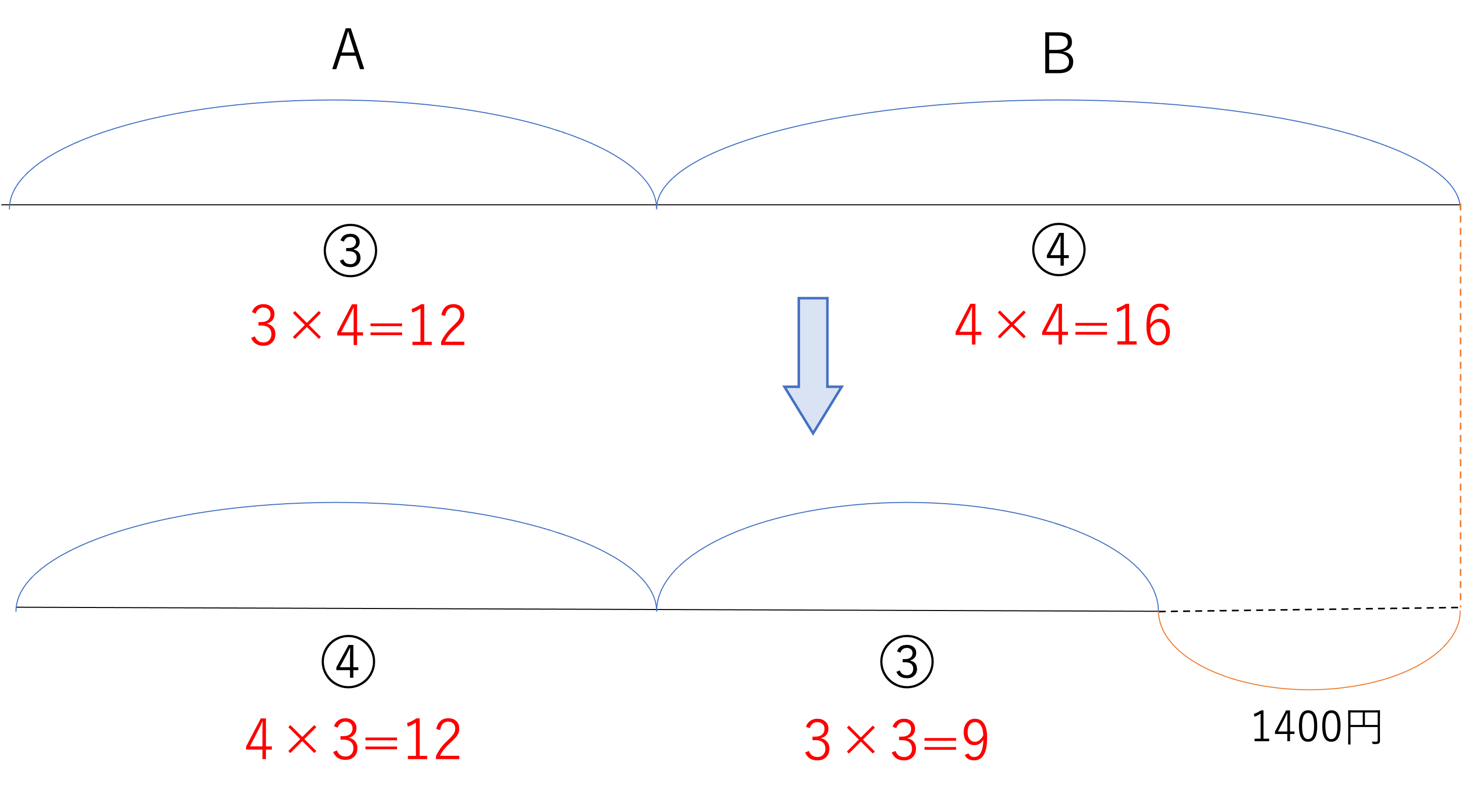
このようにして比を揃えてあげると,1400円という数字が「7」に相当することが明らかになりますね。そしてAの所持金が「12」に相当していることを考えると,次のような計算ができ,答えは2400円となります。
7:1400=1:200=12:2400
A.2400円
いかがでしたでしょうか。変化しない量に注目して比を揃えるという作業は基礎編でそこまで詳しくお伝えしませんでしたが,覚えておかないと問題が正確に解けなくなるポイントの1つだといえます。ぜひ早いうちから慣れてしまいましょう。
問題②
それでは第2問に移りましょう。この問題は,1問目に比べてお金の移動が少し多くなります。線分図の書き方に注意しながら解いてみましょう。
兄と弟の持っているお金の割合は3:1でしたが,兄は800円の本を買い,弟は母から1000円もらったので,持っているお金の割合は11:10になりました。弟がはじめに持っていたお金は何円でしたか。
(大宮開成中学校(2016),一部改題)
解説②
こちらは前回の例題と少し近いタイプの問題になりますね。2人ともにお金のやり取りが発生しているのですが,このとき変化がない部分がありません。そのため比を揃えるときに注目する部分に悩むでしょうが,ひとまず線分図に問題の要素をまとめてみましょう。
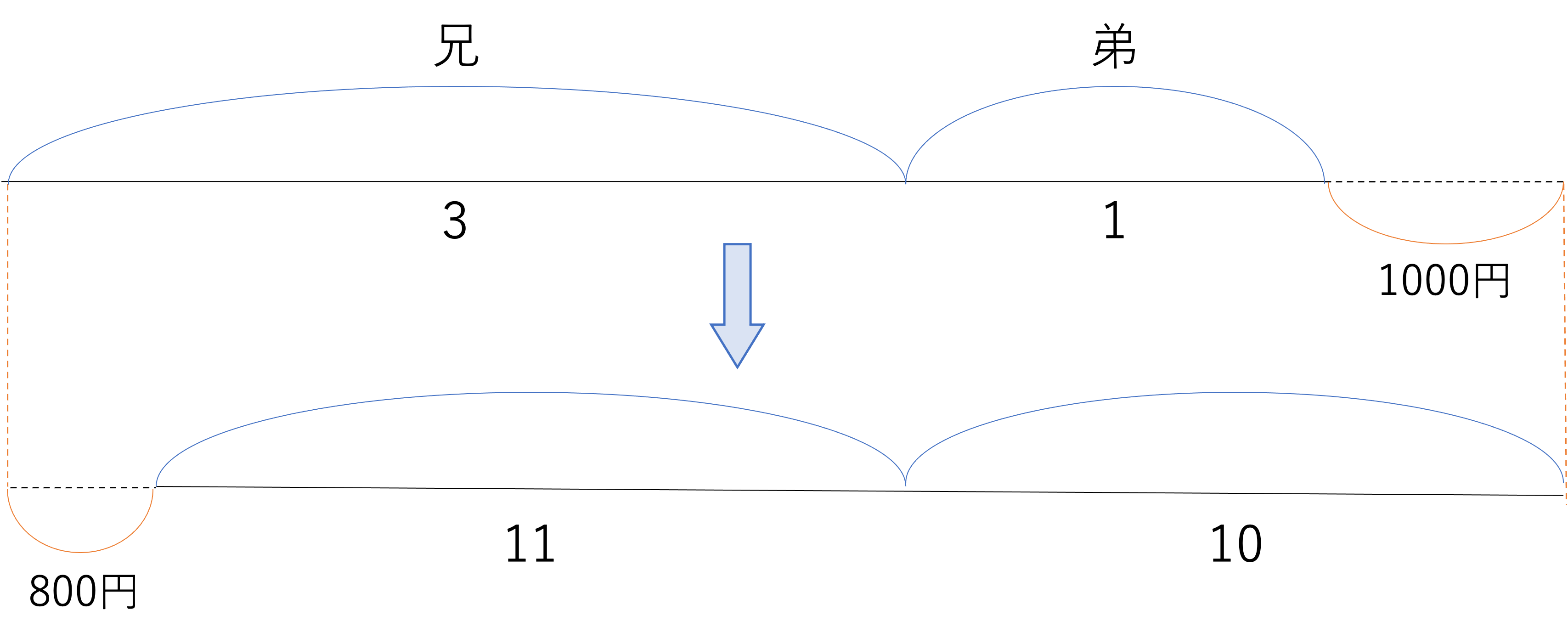
さて,問題をまとめられたところで,やはりぶつかってしまうのが,どこの比を揃えればいいのかという壁です。ここで今回は還元算・相当算における□を使った計算というテクニックを活かして計算を進めていくことにしましょう。もちろん線分図の一部を揃えたりして計算してもいいのですが,なかなか解説が分かりづらくしまう上に,時間もかかりやすいと考えられます。そこで,実際に本番の入試でこのような厄介な問題が出てきたり,計算の答えが辻褄と合わなかったりするときの代替案としての計算方法を覚えておく方が有効だと考え,□を使った計算にシフトして進めていきましょう。
さて,今回は初めに弟が持っていた所持金が求められているので,その部分を□円とおきましょう。すると3:1という比の関係から,兄が持っていた所持金は(3×□)円と表せます。更にその後のやり取りのことを考えると,弟は1000円をもらっているので所持金は(□+1000)円に,兄は800円使っているので(3×□-800)円になる,と言うことができそうです。これらのことをまとめると下図のようになります。
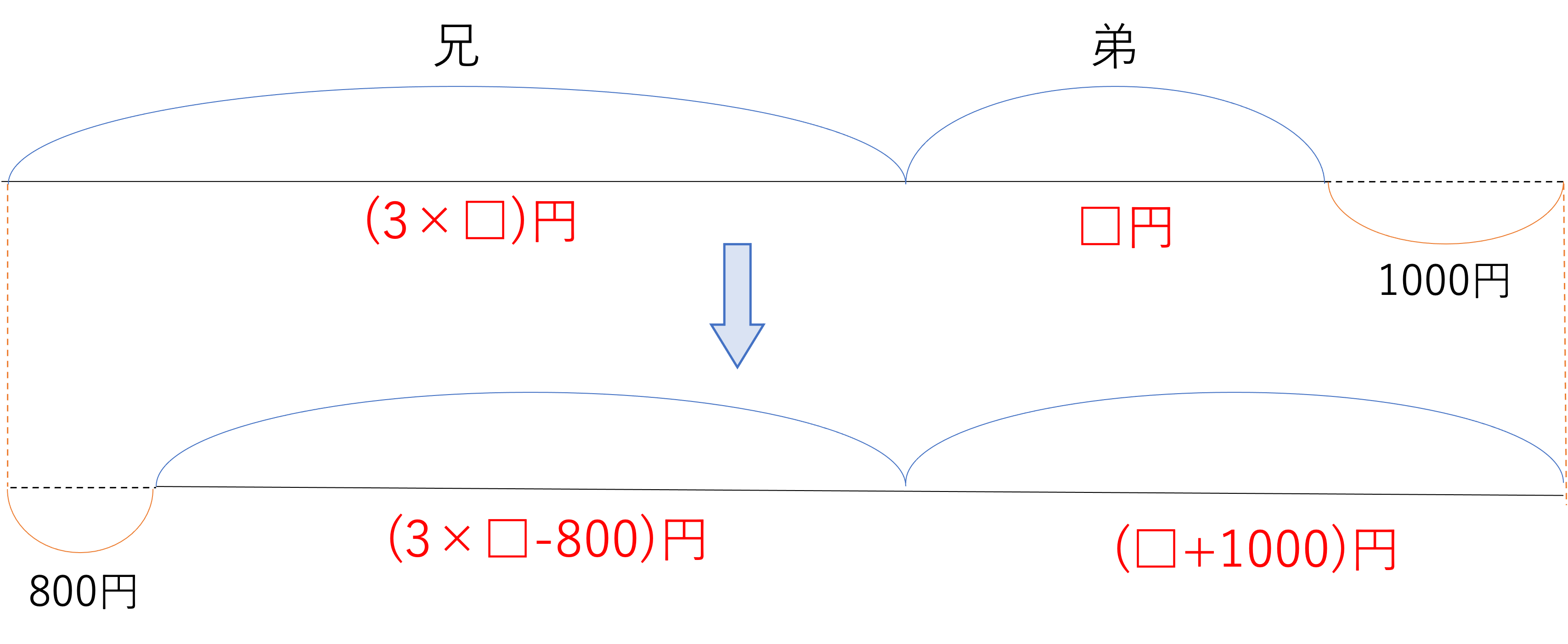
さてこの図と前掲の図を見比べると,所持金をいくら持っているかという関係と比の関係が結びつくことが分かりますね。このことから次のような式が成立し,□の中身がいくつになるかを考えていくと,答えは1000円となります。
3×□-800:□+1000=11:10
11×(□+1000)=10×(3×□-800)
11×□+11000=30×□-8000
19×□=19000
□=1000
A.1000円
このようにアプローチを変えてみるというのも,中学受験の算数を乗り越える上では大変有効な手段の一つです。難しい問題に出会ったらぜひ試してみてください。また,答えがわかっている問題を何種類かの方法で解いてみる,という演習を積んでみるのもいいでしょう。
問題③
では最後の問題に移ります。この問題は倍数算のように見えないですが,実は倍数算につながる要素が隠されています。どの要素が似ているかな,などと考えながら解いてみましょう。
次の□に適する数を書きなさい。
現在のA君とお父さんの年れいの比は1:3です。8年後のAくんとお父さんとの年れいの比3:7になります。現在のA君の年れいは□才です。
(山手学院中学校(2015),一部改題)
解説③
この問題は実は年齢算と言われる別の問題で,本来は倍数算として扱うものではないかもしれません。しかしよくよく問題を注意して見ると,2つの割合が登場していて,数が増えたり減ったりしているという定義から考えると,倍数算の要領で解くことも可能だということで今回引用してみました。このように中学受験の文章題と言うものには,実はふわっとした垣根しか存在しません。1つの問題に対して別々の角度からアプローチが取れるくらい,余裕が持てるように様々な問題を満遍なく良いでしょう。
それでは解説の本編に移ります。3問目ということで線分図は簡単に書いてしまっても良いでしょう。ただし,慣れてない読者の方はじっくり読んだり分析したりすることから始めてみてください。さて,今回の問題を図に起こすと次のようにまとめられます。
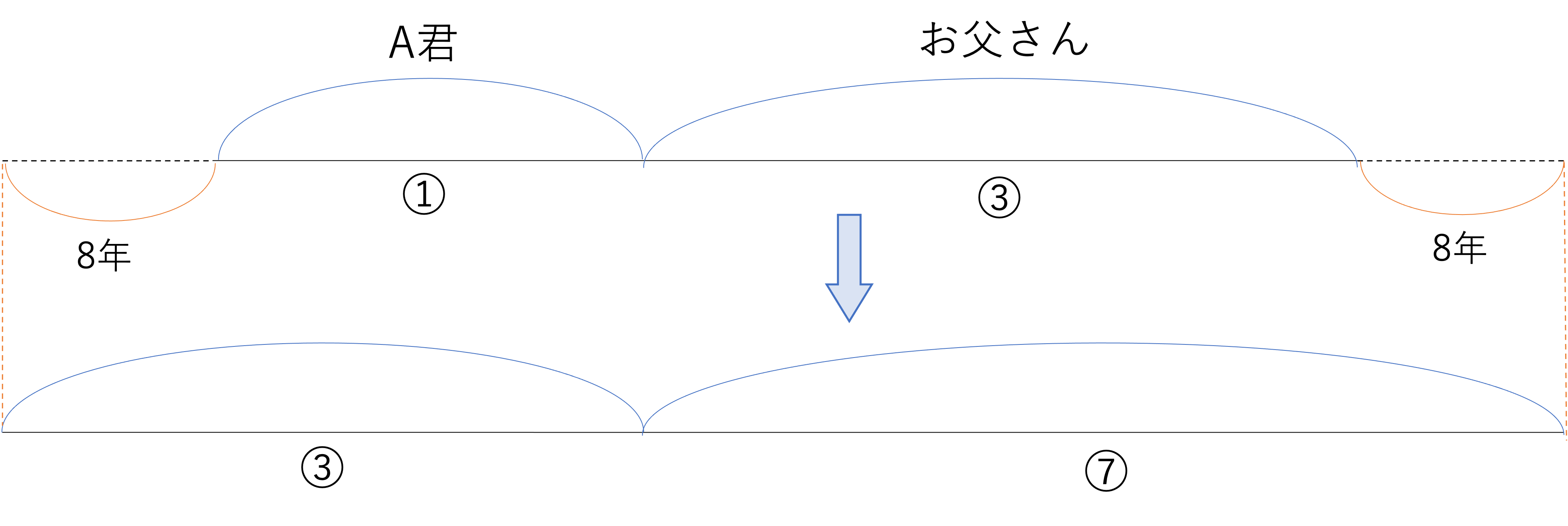
今回の図を作るポイントは,「8年後」をA君の年齢もお父さんの年齢も8つ増えた,と読み替えてあげることにあります。このように言い換えることで,見慣れない問題も線分図にまとめることができるようになります。覚えておきたいテクニックの一つですね。
さて,この問題も2問目と同じように一致している部分がありません。当たり前ではありますが,A君の年齢もお父さんの年齢も,そして2人の年齢を合わせた合計も,全てが初めの状態と8年後では異なってきます。そこで今回も有効なのが,□を使った計算に置き換えることです。今回は現在のA君の年齢が求められているので,その年齢を□才としましょう。このとき1:3という関係から,お父さんの年齢は(3×□)才だと判断できますね。そして2人の8年後の年齢は,それぞれの年齢に8を加えればいいわけですから,A君が(□+8)才・お父さんが(3×□+8)才となります。
この図に書いたそれぞれの年齢と先程の図に書いた年齢に関する比を見比べると,8年後のA君とお父さんの年齢についての関係を式として表せることに気づくかと思われます。そしてこの結びつきに沿って計算を進めていくと,□の中身が16だと分かり,本問題の答えとなるA君の現在の年齢は16才ということになります。
□+8:3×□+8=3:7
3×(3×□+8)=7×(□+8)
9×□+24=7×□+56
2×□=32
□=16
A.16才
このように,中学受験においては1個の問題でも,様々な解き方で答えを導き出したり,様々な方法で問題文を整理したりすることが可能です。前述したように,ぜひ日頃から別の解き方はないだろうか,と頭を働かせる訓練を積んでおくといいでしょう。
まとめ
今回の記事は倍数算について解説していくシリーズの第2本目として,受験に登場した問題を紹介しながら,攻略法をおさらいしていくものでした。この記事の中で引用したのは一部の受験問題に過ぎませんが,どんな問題を攻略する上でも必要となる分析や線分図といったテクニックが倍数算の攻略には詰まっています。その点をお伝えできていましたら幸いです。


















