中学受験で一番難関だと考えられるのは受験算数でしょう。小学校では習わない内容が出題されることもありますし、文章題、図形問題、その範囲はとても広いものです。
特に受験算数でつまずく原因として大きなものに「計算ミス」が挙げられます。受験生を指導していると、途中式をきちんと書けているのに最後の計算でミスしているケースをよく見かけます。また、保護者の方から受ける相談も「うちの子は計算ミスが多くて算数で点数を落としているんです」というお悩みが少なくありません。
では、ご家庭で計算ミスを発見した場合、お子さんにどのように声をかけていらっしゃるでしょうか?よくあるのが「もっと注意深く計算しなさい」「ていねいに計算しないから間違える」と言ってしまいがちです。たしかに、計算問題は注意深く、ていねいに数字を扱わなければ正解できません。しかし、「注意深く」「ていねいに」というのはいわば精神論であって、実際に手を動かして計算をするうえではあまり役に立たず、計算ミスはなくなりません。計算ミスを克服するには、具体的な指示、具体的な方法論があるのです。
今回は、計算ミスを減らすためにはどうしたらよいか、具体的な克服法をご紹介します。それとともに、筆算の過程でミスを重ねているお子さんが多いので、そういった「もったいないミス」を減らし、正解できるようにするための注意点についても考えてみましょう。
Contents
計算ミス克服法①計算を複雑にしない
計算問題で使うのは四則計算(たし算、ひき算、かけ算、わり算)です。これらが複雑に組み合わされて計算問題として出題されるのが入試問題です。四則計算の中で最も計算ミスにつながりやすいのはずばり「わり算」です。わり算はそれ単体だけでなく、かけ算やひき算も関わってくるため、計算が複雑になりやすいと居特徴があるからです。また、桁の多い数どうしのかけ算も計算力がしっかりしていないと失敗してしまいがちな関門です。計算ミスを克服するためには、複雑なわり算、かけ算を避けることがとても大切です。
でも問題が複雑なわり算、かけ算になっている場合はどうすればいいの?と思いますよね。そこで発想の転換が必要になるのです。つまり、「複雑な計算」を「やりやすい計算」に変えてしまうのです。これが計算ミスを克服する第一歩だと言えるでしょう。
たとえば、三角錐の体積を求める問題を考えてみましょう。いわゆる「錐体」の体積を求める公式は「底面積×高さ÷3」です。これはテキストの基本事項として出てきているので、皆さん覚えていますよね。基本的にはこの公式を使って三角錐の体積を求めていくわけですが、そこに計算ミスの落とし穴が隠れています。以下の三角錐の体積を求める場合、皆さんはどのように計算しますか?
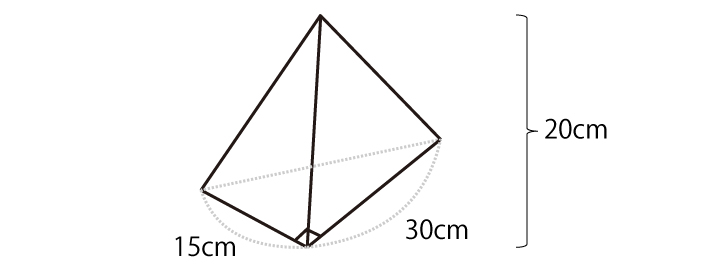
受験生の実に多くが、まず底面積を求めてから高さをかけて3で割るという、公式通りの答えの求め方をします。その場合、まず底面積を以下のように求めることになりますね。
15×30÷2=15×15=225
そして高さの「20」をかけ、最後に「3」で割る、という方法をとるのでは?と思うのではないでしょうか。ここに計算ミスポイントがあります。底面積をわざわざ求めることが実は効率的ではないのです。計算ミスを避けるためには、以下のように計算すると間違えないでしょう。
15×30÷2×20÷3
この三角錐の体積を求める式を立ててから、計算の工夫をするのです。まず、割り算部分を分数を使って書け算にします。すると以下のようになりますね。
15×30×1/2×20×1/3
30×1/3と、20×1/2というふたつのかけ算が出てきますね。それぞれ答えは「10」です。つまり、最初の式は以下のように簡略化できます。
15×10×10=1500(㎤)
このように、逆数を使ってわり算をかけ算にすることは、分数の計算ではよく出てきますよね。整数の計算においてもこの手法を使えば、一見複雑で一つひとつひやひやしながらわり算やかけ算をする必要がなくなるため、計算の工夫をすれば複雑な計算問題が単純化できるわけです。
また、約分をするというと分数の計算のイメージを持つかもしれませんが、数字を約数で割るという工夫は、分数の計算以外にも使えることが分かります。
約分というと分数計算のイメージですが、複数の数字を公約数で割るという発想は分数計算以外でも使えます。
たとえば、以下のような計算問題はどのように解くでしょうか。
7×4×□=42×12
両辺(=の左側と右側)に×しかありませんね。このような式の場合、両辺を公約数で割ることができます。「42×12=504」を「7×4=28」と考える人がほとんどだと思いますが、ここに公約数の考え方を入れ、「右辺の42を左辺の7で割る」「右辺の12を左辺の4で割る」というふたつの計算にしてみたらどうでしょうか。
42+7=6
12÷4=3
そうすると、答えは6×3=18ですね。
このように、計算を簡単にできないかな、と考えて、わり算やかけ算が混在している計算は分数を使ってかけ算だけにしたり、公約数の考え方を使って両辺の計算を簡単にすると言った計算の工夫をおこなうことは、計算ミスを減らすのに大いに役立ちます。すぐにできる方法なのでぜひやってみてくださいね。
計算ミス克服法②分配法則をうまく利用
小学校でも計算の工夫として「分配法則」を学習しますよね。分配法則は、同じものを( )の外に出して計算します。非常に便利ですよね。たとえば以下のような形で分配法則が使えます。
〇×△+□×△=(〇+□)×△
〇×△=□×△=(〇-□)×△
何気なく使っているかもしれない分配法則ですが、この「同じものを外に出す」という計算は、特に円に関わる計算で非常に役に立つのです。
たとえば、半径4cmの円の中に半径2cmの円があり、内側の円の外側の面積を求める、という一行問題はよく出題されますよね。この際に派分配法則を使うと計算が簡単になります。
4×4×3.14-2×2×3.14
これを左から順番に計算していくと手間がかかりますが、共通している「3.14」を外に出すと急に簡単になります。
(4×4-2×2)×3.14=12×3.14=37.68
解答は37.68平方センチメートルになります。
3.14のかけ算を2回おこなうと手間ですが、一度で済むと圧倒的に簡単になります。このように分配法則は非常に役に立ちますが、単純な分配法則以外にも素因数分解(整数を素数のかけ算で表すこと)を利用すると、一見分配法則が使えないように見える計算でも使えることがあります。たとえば、以下の計算問題を考えてみましょう。
25×28-15×14
これを分解すると、5×5×2×2×7-3×5×2×7となります。
「5×2×7」が共通しているので、「5×2×7×(5×2-3)=10×7×7」」と形を変えられます。それぞれを計算すると、「10×49=490)となるので、2桁のかけ算を2回とひき算1回から、2桁のかけ算1回に計算を減らすことができます。
このような一見関係ないような整数問題の法則も、四則計算を正確にするために役に立つことがあるので、関連付けて計算にどんどん使ってみましょう。
計算ミス克服法③数量感覚を養う
計算をしていて、「あれ、おかしいな」と思う感覚も、計算ミスを減らすためには非常に重要です。いわば「数量感覚」ともいえるもので、整数をかけているのに答えが小さくなったり、小数をかけたのに答えが大きくなったときに「これはおかしい、どこかで間違えている」と瞬時に判断できる力です。
この数量感覚があると、計算をしているプロセスでミスをしないようになるだけではなく、一度出した計算結果を見て「どこかおかしい」と気づくことができるので、計算ミスを大きく減らすことができます。この感覚は、もともと優れているお子さんもいるのですが、そうでなくても日常的に数値の見方を意識していれば誰でも習得できるものです。これに気づくか気づかないかによって、受験算数の成績は大きく変わるので意識したいポイントです。
たとえば、よくある計算ミスを考えてみましょう。「71×3.14=222,84」なのに、「22.284」というように小数点をつけるところを間違えてしまうミスは少なくありません。よく考えてみれば、「71は70に近い」「3.14は3に近い」といったように概算すれば210よりも答えが大きくなることは一目瞭然です。そうすると、答えが「22」になるのはおかしい、とわかるはずですよね。
ここまで細かくなくても、3.14が3に近いのであれば、71にかければ71より大きくなるはずなのに小さくなるのはおかしい、という間違いに気づくことができるでしょう。
かけ算の中でも分数や1以下の小数が入っている場合は別ですが、ある数に1よりも大きな数をかければ、計算結果はもとの数よりも大きくなることは誰でもわかることですよね。逆に1より小さい数をかければもとの数より小さくなります。わり算の場合は大きな数で割れば答えは小さく、小さな数で割れば大きくなります。
こういった数値の見方、感覚を持っていると、計算している途中で間違いに気づくことができるので傷が深くならないうちにリカバーできます。こういった数量感覚を意識しながら日々の計算問題に取り組んでみてください。
複雑な計算は筆算なしでは難しいのが現実
皆さんは計算問題を解くときに、筆算をしますよね。複雑な計算のときほど問題用紙の余白は多くの筆算で埋め尽くされるでしょう。筆算は算数の計算の解法のひとつであり、計算の経過を書いていくものです。ただ書き散らかして一部を計算するというものではありません。そこに注意が必要です。
中学受験の計算問題では桁数が大きいと暗算で解くのはまず無理ですよね。また、計算も長く、一度の計算で魔法のように解けるようなものばかりではありません。そこで、ひと桁ごとに計算のプロセスを書いて残しておくことによって、複雑な計算を間違えることなく解くのに役立つのが筆算です。
筆算をうまく使えば、複雑な計算問題も簡単にすることができます。また、プロセスを残すことができるので、見直しをしたり、間違えている箇所を見つけることが簡単になる、つまり大きな計算問題を小さく区切って計算していくイメージです。中学受験の複雑な計算問題においては、筆算なしで解くのは非常に難しいと言えるでしょう。それだけうまく使えば得点に寄与してくれるのが筆算です。
筆算をうまく活用すると、複雑な計算問題も少しずつ解いていけばよいので、計算問題アレルギーを克服することができます。ただし、筆算をするときには守るべきルールもあります、それがないと、完璧な手段にならないので、筆算の途中で計算ミスを引き起こしてしまうことがあるので注意が必要です。筆算を行う際の注意点について確認しておきましょう。
筆算で間違えないための注意点
複雑な計算問題を簡単にしてくれて、プロセスも残しておける便利な筆算ですが、そんな筆算の途中でミスをしてしまい、間違えてしまったという経験は受験生なら誰でも持っているのではないでしょうか。
筆算で計算ミスをしてしまうお子さんにはいくつかのクセがあります。そのクセを見ながら、どのようにすれば筆算で間違えないで済むのか具体的に考えてみましょう。
筆算の注意点①字はていねいに書く!
筆算に限らず、ケアレスミスの多いお子さんには、「字が雑」という共通項があります。とくに数字は簡素で画数も少ないだけに、雑に書いてしまうといったい何という数字なのかわからなくなってしまうことが起こり得ます。たとえば「3」と「8」などは多い間違いですし、焦るあまりに「6」と「9」を取り違えてしまうことも少なくありません。
せっかく筆算で複雑な計算問題を簡略化して解きやすくしていくのに、書いている数字が分からなければ結果としてその計算で間違えてしまうことは目に見えています。本人が分かればそれでいい、という考え方もあるかもしれませんが、あとから問題用紙を見返して解読不能な数字を書いている場合は、解答欄の数字も間違いなく解読不能になっているでしょう。
途中式を書かせる問題では、その部分が×になってしまいますし、第一解答も雑に書いているでしょうから、いくら正解していたとしても読めないのでアウト、ということになってしまいます。誰が読んでも、特に採点者が読んでわかる数字を書くことは入試はもちろん、模試や小テストでも絶対に必要なことです。
特に入試は、解答用紙を通して採点者、つまり志望校と対話をするものです。そこでいい加減な字を書き、相手が読めないようではイメージが悪いばかりか採点してもらえないこともあり得るのが現実です。クセがある字を矯正するまではしなくて良いですが、少なくともていねいに、読んでもらえるような字を書くという意識は必須だと言えるでしょう。
「自分が書いた字だから自分が読めればいい」という受験生や、「本人が分かっていればそれでいい」とおっしゃる保護者の方は多いのですが、制限時間の中で問題を解いていると焦ってしまい、自分の書いた字も判読不能になってしまうことは少なくないことに注意が必要です。自分、採点者、誰が見てもわかるようにていねいに字を書くことが大切だということを意識して、普段の学習から習慣づけておきましょう。
筆算の注意点②補助数字を端折らない
筆算をするときに、繰り上がりや繰り下がりが生じたときに、横にいくつ繰り上がるのか、繰り下がるのか小さく書きつけておきますよね。あれが「補助数字」です。筆算を行う際は、この補助数字が非常に重要です。見直しの際にどこで桁が変わったのかなど、計算の正確なプロセスを追うことができるので、必ず残しておきたいところです。
しかし、桁数が少なかったり簡単な計算問題だったりすると、ついつい補助数字を省略してしまうという受験生は少なくありません。もちろん九九で簡単に解けるような計算まで補助数字は必要ありませんが、受験算数の計算問題はいくつもの過程を経て正解にたどり着くという複雑なものです。
ですから、補助数字を端折ってしまうことは非常に危険ですし、見直すときに手間がかかってしまい、点数を落としてしまうことにつながりかねないので注意が必要です。補助数字をきちんと書いておくだけで、見直しが楽になり、無駄が省けるだけでなくケアレスミスも亡くなっていくという効果があります。
これは簡単だし、手っ取り早く計算できるから補助数字をわざわざ書かなくてもいいのでは、かえって手間がかかって時間の無駄では、と思われるかもしれません。しかし、その一瞬の心のスキがミスを生むのです。補助数字を書くことは、習慣化してしまえばわざわざ意識しなくてもできるようになります。これで見直しもしやすくなり、ケアレスミスが減るのであれば、端折る意味はありませんよね。ぜひ、習慣づけて、なぜ繰り上がるのか、繰り下がるのか、計算結果の検証に役立てるようにしておきましょう。
筆算の注意点③限られたスペースで筆算する練習も
自宅学習で計算をするときや塾で問題を解くときは、ノートを使って余白に広々と計算、筆算をしたり図を描いたりできますよね。また、入試においても計算用紙が問題用紙と別に配られる中学校もありますが、すべての中学校でそうとは限りません。また、模試では計算用紙は与えられませんので、実際にテストを受けるときに計算用紙が与えられないという場合に備えた計算練習を行っておくことも必要です。
また、途中式を書く問題を出題する学校の場合、決められた枠の中に途中式から考え方、計算まで書かなければいけません。いつも広々としたノートに好きなだけ大きな文字で書いていると、実際の入試の解答用紙に対応することができなくなる恐れがあります。
そういう場合は、問題用紙の余白などを使って途中の計算などをおこなっていくことになりますが、テストの解答用紙の決められた解答欄や余白を使って計算や作図をしなければいけないときの対策をとっておく必要があります。得に模試はまず計算用紙は配られない(学校別模試の場合は配られることもありますが)ので、問題用紙の狭い余白に筆算していくことが多くなるでしょう。
普段からノートに広々と筆算をすることは、計算ミスをなくすためには重要です。計算問題が苦手なのに狭いところにこちょこちょ書いていると間違いのもとになり、見直しもできないので、苦手な場合はまずそういった大きなスペースで計算問題を克服するのが先決でしょう。
しかし、模試や入試ではいつもと異なる条件になるので、いつもの習慣と違うと実力を発揮しきれなくなることもあり得ます。お子さんは、いつも練習してきたことはできても、とっさのとき、しかも独特の緊張感のある模試や入試の現場では応用が効かないことが少なくありません。小さなスペースでおこなった計算が思ったよりも複雑で、筆算を多用しなければいけなくなり、どこに何を書いたのかがわからず見直しができなかった、ということはよくあります。
対策としては、日ごろから入試問題の解答欄を意識して、限られたスペースで計算や作図ができるようにしておくことと、問題用紙の余白などにどこに何を書いたか振り返れるように小さくてもていねいに筆算を残して置き、見直しができるように習慣づけることです。入試ではいきなり出題傾向が変わることもあります。そうしたときにあわてないためにも、限られたスペースでも対応できるようにしておきましょう。
筆算の注意点④どこに何を書いたか振り返れるようにしておく
これはよく模試の振り返りをするときに噴出する問題なのですが、制限時間の中でたくさんの問題を解いていくうちに、余白部分が筆算や計算結果で埋め尽くされてしまうことはよくあることですし、解くためにはそれは必要なことです。しかし、あまりにたくさん、小さく書くこと、そして急いで書くためにとびとびに筆算を書いてしまうことは良く起こるので、大問3を解いていたのに大問2の近くに筆算を書いてしまったために見直しができなくなってしまった、ということは少なくありません。
せっかく頑張って問題を解くのですから、見直しをその場でして正解を積み重ねていきたいですよね。そういった「どこに何を書いたかわからなくなる問題」を解決するためには、ひとつの問題を解いたときに書き込んだ式や計算、筆算を丸などで囲んでひとつのまとまりにしておき、それを問題に矢印で結んでおくことをおすすめします。そうすると、どの問題についての計算や筆算なのか、式なのかということが一目でわかります。できれば左から解法の順番に書いておくと痕から見ても見直ししやすいです。
このようにひとまとまりにしてどの問題を解いたプロセスなのかが分かるようにしておくと、その問題を解いた後すぐに見直しができ、チェックも格段に速くできるようになり、間違いも発見しやすくなるので確実に正解数が増えていくのです。
どこに何を書いたかわからなくなってしまった、という受験生は少なくありません。あとから探すのに時間がかかりすぎると制限時間内に終わらないと焦ってしまい、次の問題にも影響が起こってしまいかねません。確実に正解できる問題を制限時間内に、できるだけ多く解くこと、それが受験算数で高得点をとるコツです。無駄な時間を省くためにも、工夫をして自分なりの解答プロセスを見返すことができるように意識して模試やテストを受けてください。
そして、結果が返ってきたら、成績表だけ見るのではなく、答案用紙、そして筆算や解答のプロセスが書いてある問題用紙をしっかりチェックしましょう。受験生を指導する私たちは、何よりもまず問題用紙を見てどのように解いていったかそのプロセスを見ます。そこに何が書かれているのかを見てはじめて次の課題が見えてきます。
そのため、ご家庭でも問題用紙の使い方には気を配っていただき、どの問題を解くときに白紙になっているのか、どの問題を解くときに混乱しているのか、といったことをしっかりチェックしておき、次に克服するべき点を意識することをおすすめします。テスト後に塾の先生に相談し、問題用紙の使い方やテストへの向かい方をアドバイスしてもらってもよいですね。
計算ミスは習慣化すれば減らせるミス
計算ミスは一番やってはいけないミス、だと思いますよね。たしかに、いくら途中式があっていても、解法があっていても、最終的に計算でミスをして解答が間違っていると大きな減点になりますし、解答だけを書くタイプの出題をおこなう中学校(海城中学校など)では、途中プロセスを見てもらえないので0点になってしまいます。
海城中学校ではなぜ途中式を書かずに解答だけ書かせるのかと言うと、解法プロセスが合っているのは当然の前提条件、最後まで見切って速く正確な計算力で正解を導き出す力を重視しているからです。決して途中のプロセスをおろそかにせよということではなく、それを前提として最後まで解ききる力をつけてきてくださいね、ということです。
計算ミスは、それまでの解法プロセスをゼロにしてしまう、実は非常に厄介なミスであり、ケアレスミスと単純に片づけてはいけません。いつも同じような問題で計算ミスをしている場合は、公式や解法を理解しきれていない可能性もあるからです。そうした場合は、基礎に戻ってもう一度公式や解法を見直す習慣を徹底してください。
計算問題を完全になくさなければ、と思うと非常に焦ってしまい、かえってミスが続いたり増えてしまったりすることもあります。「こんなに頑張っているのになぜ?」と思うこともあるかもしれません。しかし、焦る必要はありません。焦っても点数は積み重ねられるものではありませんから、何よりも計算の基礎、計算の工夫、数量感覚の習慣化が第一です。
約分や計算の工夫をして、複雑な計算問題を簡単にすること、解いている間に「あれ、この答えはおかしいな、どこで間違ったかな」ということに気づけること、そして筆算をする際に手間を惜しまないこと、これを習慣化することによって計算ミスは減っていきます。
「どうしてこんな簡単な計算問題で間違えたの!」とつい言ってしまいがちですが、受験算数の計算問題はそう簡単なものではありません。複雑で四則計算の基礎と計算の工夫を駆使してようやく解けるものです。もし計算ミスをしたら、その原因はどこにあったのか客観的に分析することが重要ですが、お子さんはなかなかそれがひとりではできません。また、保護者の方が「計算問題なんてもう一度解けばいいでしょ」というお考えだと、計算ミスはなくなりません。
ぜひ、計算ミスがあったら、「すべての算数の基礎」のミスだととらえて、ていねいに客観的に分析し、お子さんと一緒にどこで間違えたのか、その原因は何なのか、ということを話し合いましょう。そして、計算ミスがなければどれほど点数が上がるのかということを具体的に数値化してみると「こんなもったいないミスはしたくない」とお子さんも思うものです。そういった働きかけをぜひしてください。
今回ご紹介した計算ミスをなくす方法、筆算の注意点については今日からすぐにできるものです。ぜひ親子で取り組んでみてください。
<関連記事>
一橋大学卒。
中学受験では、女子御三家の一角フェリス女学院に合格した実績を持ち、早稲田アカデミーにて長く教育業界に携わる。
得意科目の国語・社会はもちろん、自身の経験を活かした受験生を持つ保護者の心構えについても人気記事を連発。
現在は、高度な分析を必要とする学校別の対策記事を鋭意執筆中。





















