今回は通過算という文章題についての記事になります。この問題は攻略法が少々特殊なのですが,どの参考書も計算方法だけを書くものが多く,そのせいか考え方の基本を理解しにくくなかなか知識が定着しなくて困りやすい単元だと言えます。そこで今回の記事では,通過算の解き方を分かりやすく丁寧にご紹介していきます。よろしければ一読していただきたいです。
Contents
そもそも通過算とは?
まずは攻略法をご紹介する前に,通過算とは何かということについて触れていきましょう。通過算とは文字通り,あるものがあるものを通過するというシチュエーションにおける文章題を指します。そして,通過するということは動いているものが登場するということであり,それに関連して道のり・速さ・時間といった要素を考えなければいけません。
3つの出題パターンを覚えよう!
この通過算ですが,出題の形式には主に次の3つのパターンが存在します。そのパターンは何が何の前を通過するかで変わってきます。通過ということで必ず動いているモノが登場すると前述しましたが,通過されるものの動き方で場合分けができるということです。
パターンの1つ目は止まっているモノを通り過ぎる場合の計算です。2つ目が動いているモノを追い越す場合の計算です。3つ目が動いているモノがすれ違う場合の計算です。まずは通過算にはこれらの3つの出題傾向があるのだな,ということを理解しておきましょう。
パターン① 止まっているモノを通り過ぎる通過算
ここからはそれぞれのパターンの中身や攻略法についてご紹介していきます。まずは止まっているモノを通り過ぎる通過算ですが,こちらは文字通り動いているモノが止まっているモノを抜かしたり追い越したりするという設定がなされている文章題のことを指します。よく出るタイプの問題文が下のような文章になります。
全長400mの電車が300mのトンネルに入りはじめてから出終わるまで1分かかりました。電車の速さは時速何kmでしょうか。
この例題では電車という動いているモノがトンネルという止まっているモノのことを通過していますね。なお電車の部分がバスや車だったり,あるいはトンネルの部分が橋だったり駅だったり人だったりすることももちろんあります。それゆえに若干判別しづらいかもしれませんが,パターン①の全ての問題において共通しているのは動くモノと動かないモノの存在です。2つのモノが登場していて,そのうちの片方にのみ時間・道のり・速さが与えられていたら,それはパターン①の通過算だと判断してしまって良いでしょう。
攻略法の紹介①
それでは止まったモノを通り過ぎる通過算の中身を解説してきたところで,次は問題の攻略法をご紹介いたします。上の解説でも取り上げた例題を使いながら,どこに注目していけばいいのか考えてみましょう。今回は問題で問われているシチュエーションを図にしてみたので,いくらか問題文の中身が理解しやすいのではないかと思われます。まずはご自身で答えの導き方を考えてみるのも良いかもしれません。
全長400mの電車が300mのトンネルに入りはじめてから出終わるまで1分かかりました。電車の速さは時速何kmでしょうか。

それでは解説に移ります。まず初めにどのパターンでも大切なことが,何が求められているかを判断するということです。動きのある問題では先ほど述べたような道のり・時間・速さといった3つの要素が絡んできます。そこで求められている答えを初めに知っておくことで,どの要素に着目して計算を進めていけば良いのかを逆算して理解することができるからです。今回は電車の速さが求められているので,電車が進んだ道のりと移動時間を求めれば速さも導き出せそうだと想定できますね。また今回の問題では,移動時間が1分であったという情報が文中で与えられています。それゆえ電車がどのくらい進んだか,について考えることができれば答えを求められそうですね。
しかし,ここで間違えがちなのが,電車が通過した距離=トンネルの長さと考えてしまうことです。「電車がトンネルを通過した」と書かれていると,つい進んだ道のりは300mだと思い込んでしまうでしょうが,実際はもっと長い距離を進んでいます。というのも,電車には全長があるからです。全長があるせいで,トンネルに入ったとカウントされるのは電車の先頭がトンネルに差し掛かったときですが,トンネルを出たとカウントされるのは電車のお尻がトンネルを抜けたときというややこしいことになってしまうのです。この点を踏まえないと正しい答えを導くことはできないので,動くモノの全長・幅といったものに注意して計算を進めていきましょう。
そして全長・幅を踏まえた上で電車が進んだ道のりを求めていくには,電車の先頭が動いた距離を考えることが大切です。今回の問題だと,電車がトンネルに差し掛かってから出ていくまで,電車はトンネルの長さである300mに電車の全長400mを加えた長さ,つまり700mになります。
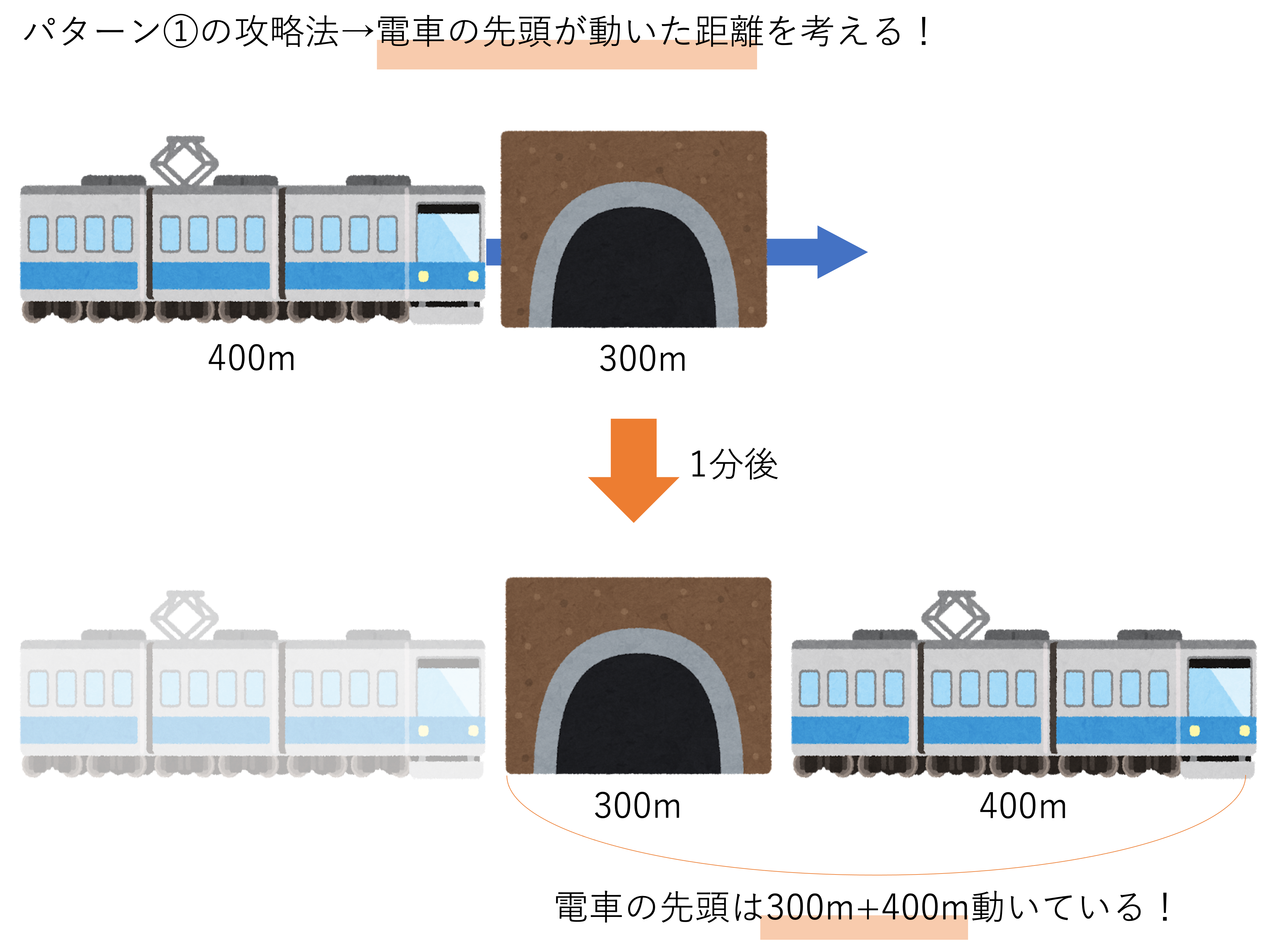
以上のことから電車の進む速さを計算して答えを出していきましょう。なお,このとき求められている単位がどのようなものであるかには気をつけておきましょう。せっかく答えが導き出せても,秒速・分速・時速といった単位を間違えてしまうだけで×になってしまいます。今回の問題では時速何kmであるかが問われているので,その形に当てはまるように計算を進めると次のような答えが導かれます。
1分間で進んだ距離(km)×60(分)=1時間辺りに進んだ距離(km)
700(m)×60(分)= 1時間辺りに進んだ距離(km)
0.7(km)×60(分)=時速42km
A.時速42km
パターン② 動いているモノを追い越す通過算
続いては動いているモノを追い越す通過算を解説していきます。パターン①で登場したのは動かないモノが動くモノのことを通過するというシチュエーションに基づく問題でしたが,今回のパターン②では同じ方向へと動いている2つのモノの関係を考えなければなりません。パターン②の典型的な問題は次のようになります。
秒速10mで走っている全長400mの電車Aが,秒速20mで走っている全長500mの電車Bに追いついてから追い抜くまで何秒かかるでしょうか。
この例題でも電車という動くモノ,そして長さや幅のあるモノが登場していますね。この問題も通過算の1つであるので,速さ・道のり・時間に注目していけば解けるはずですが,着目するポイントがパターン①と若干異なるので,その点に注意して攻略法を抑えていきましょう。
攻略法の紹介②
ということで,ここからはパターン②の問題の攻略へと移っていきます。上で取り上げた例題を再度ご紹介しますので,この問題を解きながら解答のポイントを確認していきましょう。
秒速20mで走っている全長400mの電車Aが,秒速10mで走っている全長500mの電車Bに追いついてから追い抜くまで何秒かかるでしょうか。
まずはパターン①と同じ要領で,求められている答えの方式や問題文で示されている状況の確認を行いましょう。今回の問題で聞かれているのは追いついてから追い越すまででかかった秒数,つまりは時間です。そのため道のりと速度について考えていけば良いというわけですね。またそれと同時に問題文のシチュエーションの整理も実施しましょう。今回は「電車が追いついてから追い越すまで」という指示が与えられているのですが,これを簡単に言うと,電車Aの先頭が電車Bのお尻に追いついてから電車Aのお尻が電車Bの先頭と重なるまで,ということと同じ意味になります。追いつく・追い越すという単語だけだと誤解しやすいので,どことどこが重なり合うのかについて注目しながら問題文を理解していきましょう。
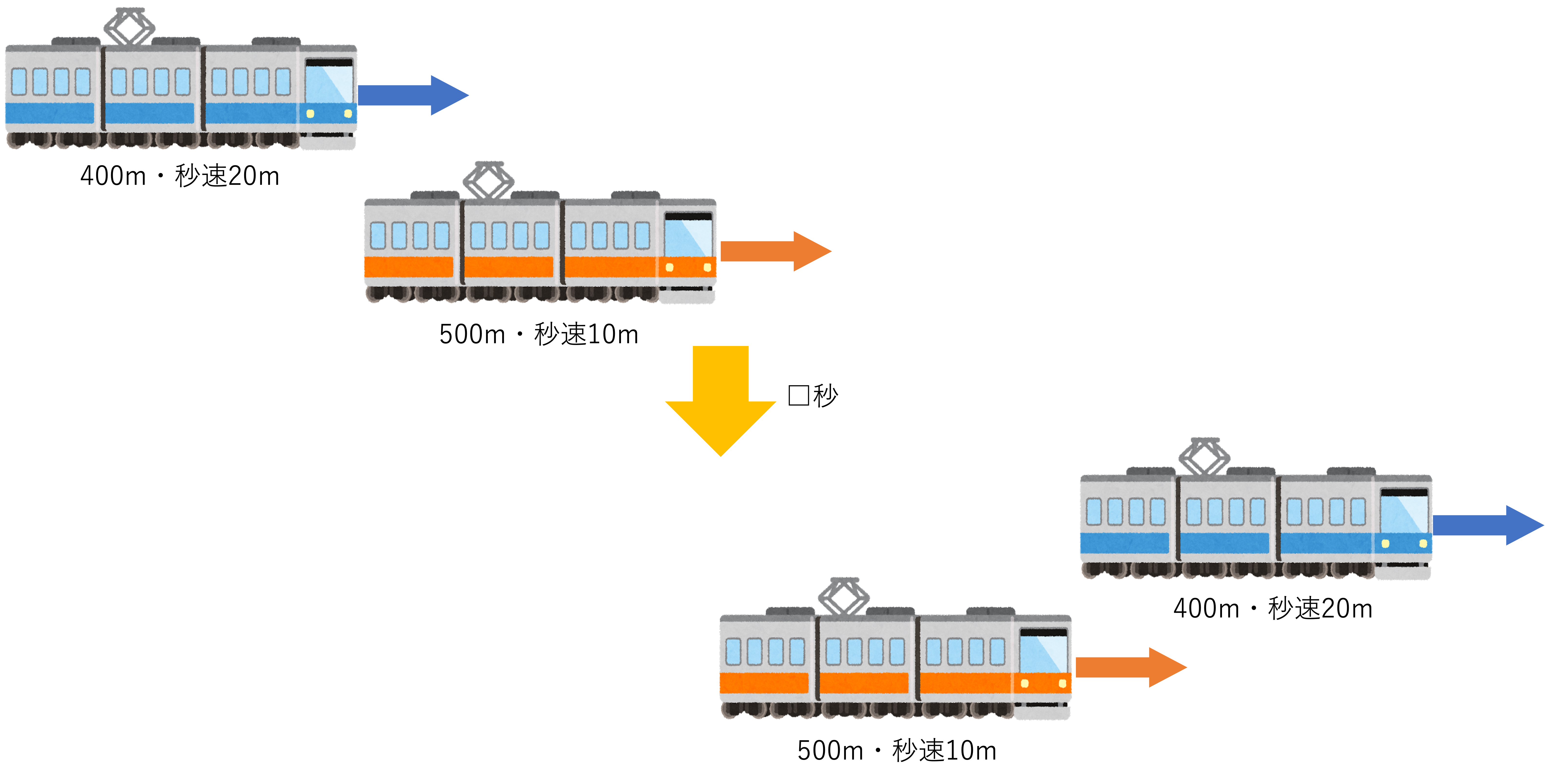
問題文の中身が整理できたところで次のステップに移りましょう。今回の追いつく・追い越すという問題において重要なのが,2つの電車の距離が次第に縮まっていくということです。電車Aは秒速20m・電車Bは秒速10mなので,2つの電車は1秒間に10mずつ近づいていくことになります。そして1秒で10m,2秒で20m,3秒で30m…と近づいていき,やがて全長500mである電車Bを完全に追い越すまでにかかった秒数が今回の答えになるわけです。
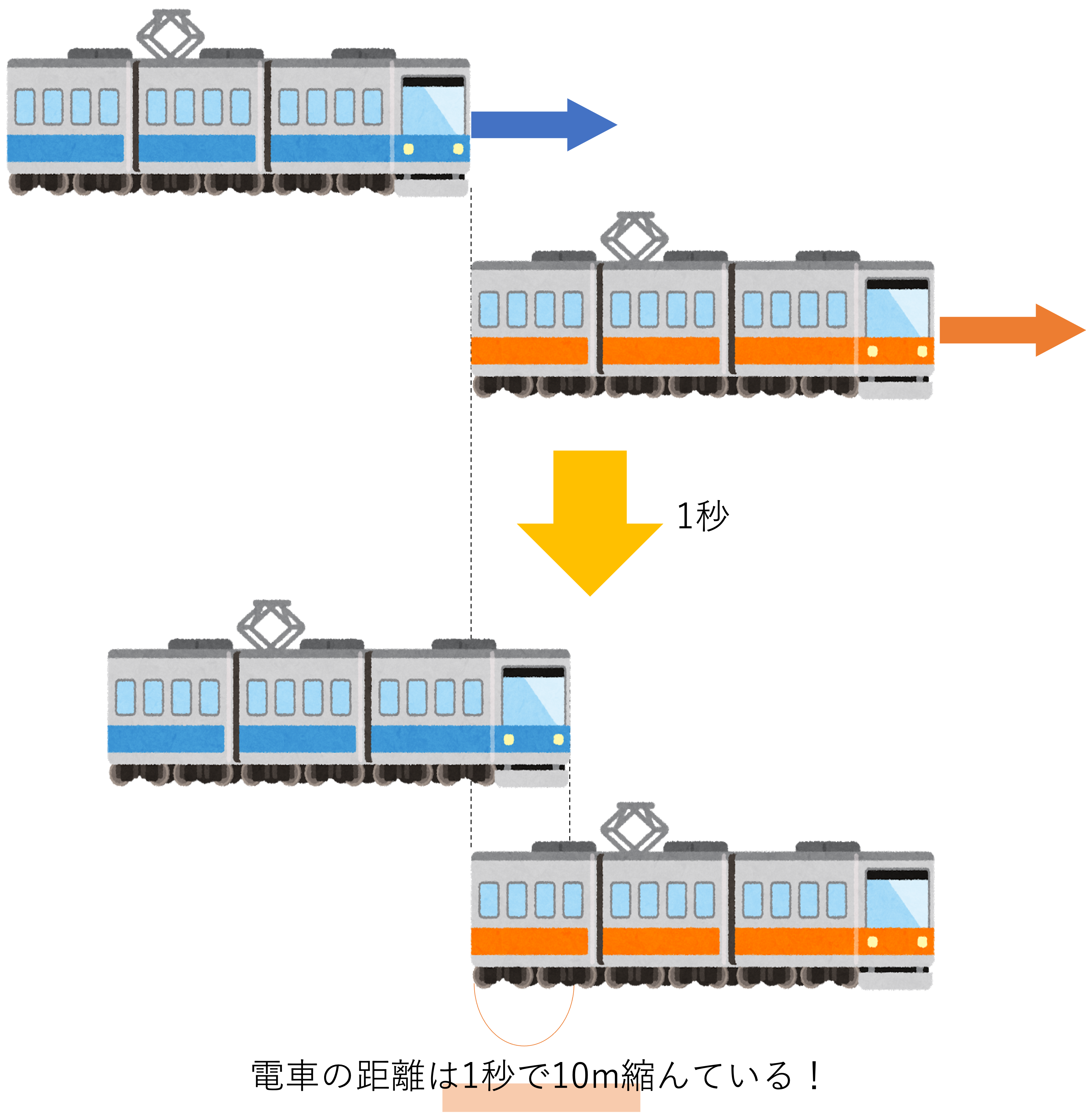
そしてこのとき重要なのが,パターン①と同様に,電車の長さや幅について考えることです。全長500mである電車Bを追い越すまでに走らなければならない距離は500mだ,と勘違いしてしまいがちなのですが,実際はそれだと足りません。この問題でも電車Aの先頭がどれくらい動いたのか,という要素に注目しないと正しい答えを導けません。先ほども確認しましたが,今回の問題では「電車Aの先頭が電車Bのお尻に追いついたとき」から「電車Aのお尻が電車Bの先頭を追い越したとき」までの長さの計算が求められているので,このとき電車Aは電車Bよりも,電車Bの全長である500mに電車Aの全長である400mを足した900m分長い距離を走らないといけないわけです。
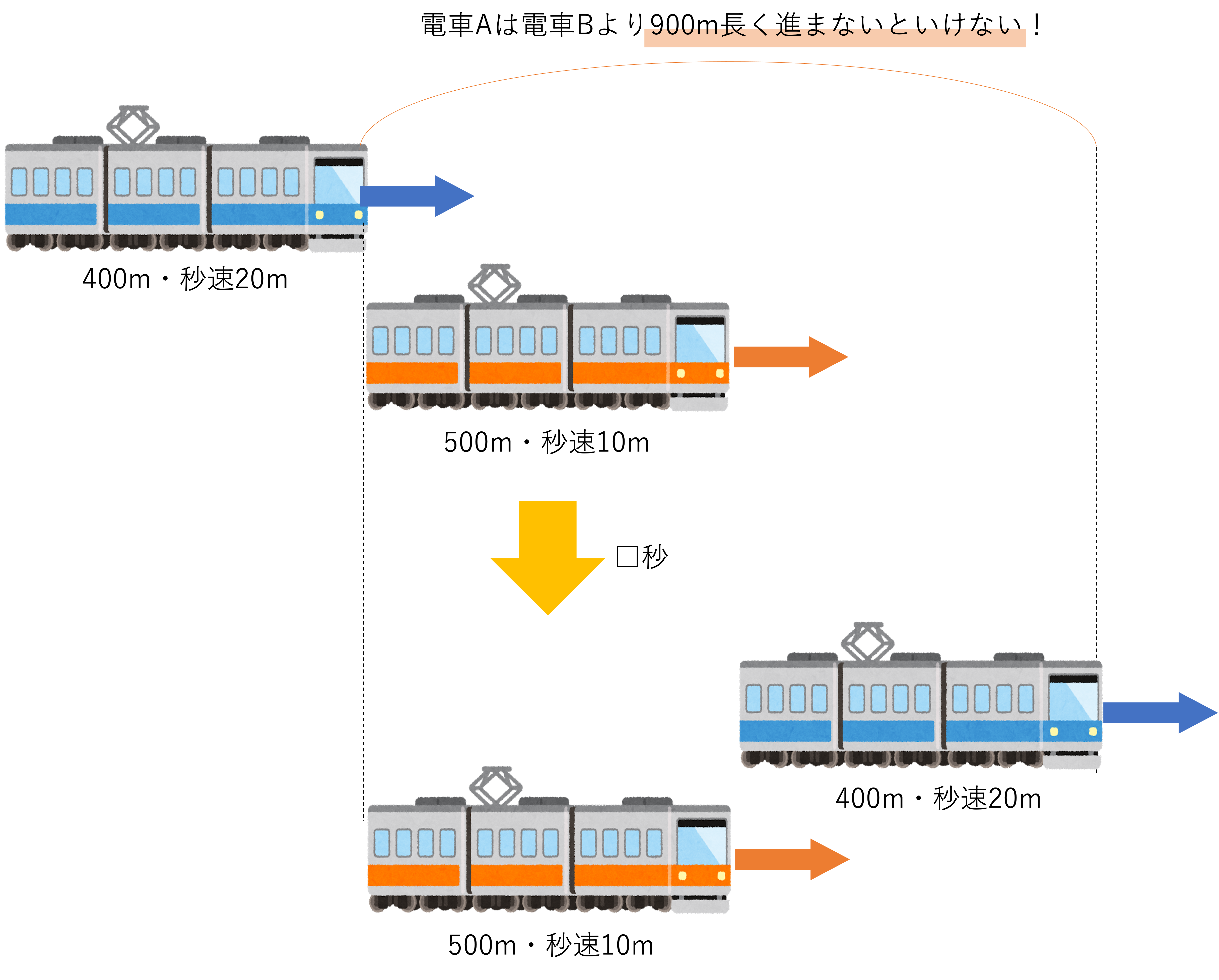
以上のことから,電車Aと電車Bは1秒間に10mずつ近づき,それを900m分繰り返せば追い越すことができる,ということが分かりました。このことを基にして計算式を立てると次のような答えが求められます。なお,今回は秒数という単位が問われていることをきちんと踏まえて答えを導きましょう。
進んだ距離(m)÷1秒あたりに進む距離(m)=かかった時間(秒)
900(m)÷10(m/s)= 90(秒)
A.90秒
パターン③ 動いているモノがすれ違う通過算
最後にご紹介するのは動いているモノがすれ違う通過算です。こちらはパターン②の問題と同じように,動いているモノと動いているモノ同士の関係についての問題になります。相違点としては動いている・走っている向きが反対であることですね。同じ方向へと進む速さの違う電車などが追いついたり追い越したりする場面と違って,ここで登場するのは反対の向きに進む電車などがすれ違うという場面です。パターン③の典型的な問題は次のようなものです。
秒速10mで走っている全長400mの電車Aが,秒速20mで走っている全長500mの電車Bと出会ってからすれ違うまで何秒かかるでしょうか。
この例題でも速さ・道のり・時間という3つの要素に注目することの重要性は変わりませんし,電車の先頭が動いた距離を考えながら計算を進めるという手順も変わりません。ただ,やはり他のパターンとは要領が異なります。上でご紹介した2つのパターンとの共通点・相違点を探しながら読み進めていただけますと幸いです。
攻略法の紹介③
それでは最後のパターン③の攻略法を,上でご紹介した例題を用いながら解説していきます。例題を再度ご紹介しますので,どのように解き進めていけばいいかを考えていただけますと幸いです。
秒速10mで走っている全長400mの電車Aが,秒速20mで走っている全長500mの電車Bと出会ってからすれ違うまで何秒かかるでしょうか。
はじめに取り掛かるのは問題文の分析です。既に2つの例題で同じようなことをしているので細かい部分は省略しますが,今回はすれ違いにかかった秒数が求められています。そのため速さ・道のりの2つの要素が分かれば答えを導くことができそうですね。そして答えからの逆算を行った後は,問題文における状況の整理に移ります。今回の問題では電車Aが電車Bとすれ違う,というシチュエーションが登場していました。ここで「すれ違う」という言葉の意味に注目してみます。すれ違うとは,2つの電車の先頭と先頭が重なってからお尻とお尻が重なるまでの通過のことを指します。そのため電車Aと電車Bのすれ違いを考えると,次のような図にまとめることができます。
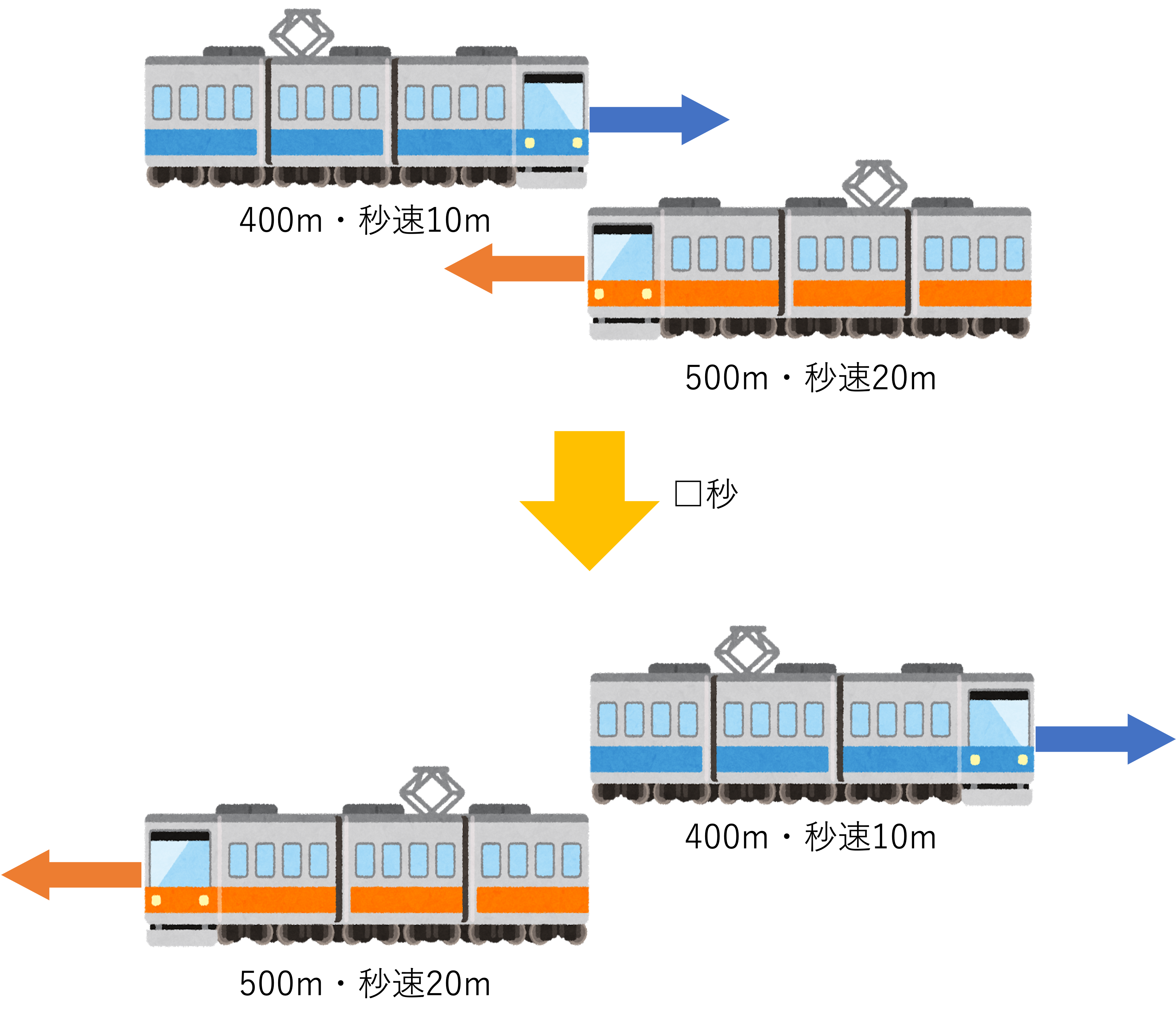
そして問題の要素を整理し切ったところで本題の計算に移るのですが,今回の問題で肝心なのが,パターン②と同様に2つの電車の距離が少しずつ近づいていくということです。この問題では電車Aが秒速10m・電車Bが電車Aとは反対の方向に秒速20mで進むと提示されています。先程の問題では2つの電車が同じ向きに進んでいたため1秒間に進む距離は2つの電車の速度の差として計算しましたが,今回は進む向きが逆向きですから,1秒進むごとに2つの電車の距離は10+20=30mずつ縮んでいくと計算できますね。
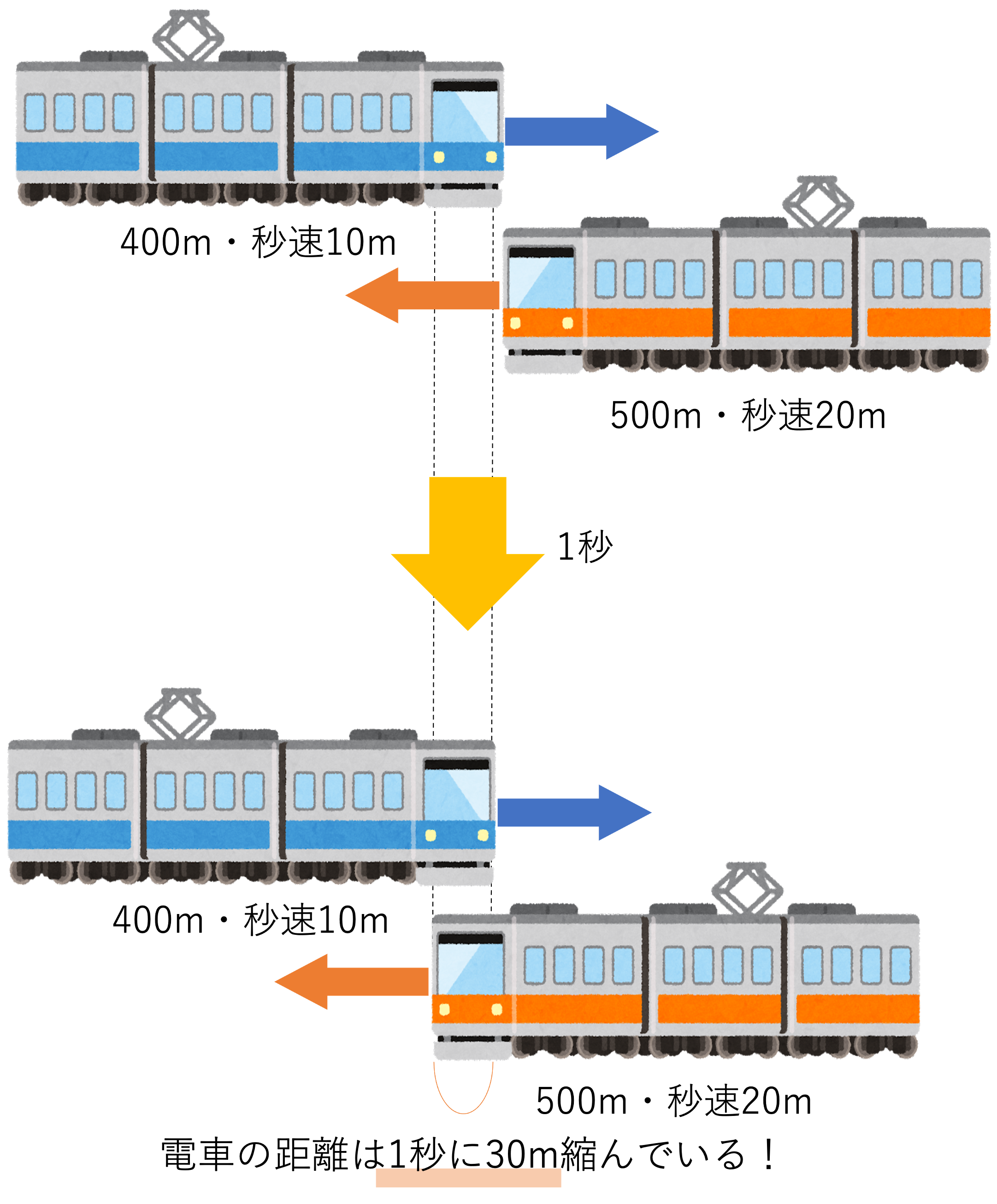
さて1秒間に30mずつ距離が変化する,つまりは速さが計算できたところで,次は電車が進んだ道のりについて考えていきましょう。止まっているモノの通過や動いているモノの追い越しは道のりが分かりやすかったですが,すれ違いだと少々動いた距離が理解しにくいかもしれません。しかし基本的なところはやはり電車の先頭が動いた距離になります。
動いているモノ同士の通過算の問題における進んだ距離とは,実際に何m進んでいるかということではなく,片方の電車を基準としたときにどれくらい前/後ろにいるかという相対的なモノです。そのためこの問題でも,電車Bを基準に電車Aが進んだ距離を計算していけば,それを道のりとして式に当てはめることができます。そしていま,問題において電車Aの先頭は次の図のように動いているため,進んだ道のりは400+500=900mとなりますね。

以上の計算から電車に関する速さも道のりも計測できたので,後は式を立てて答えを導いてしまいましょう。今回の問題ではすれ違いにかかった秒数が問われていることに注意しながら計算を進めていくと,以下のような答えを導くことができます。
進んだ距離(m)÷1秒あたりに進む距離(m)=かかった時間(秒)
900(m)÷30(m/s)= 30(秒)
A.30秒
まとめ
- 答えとして問われている要素に目を向けよう!
- 動き方・動きの向きからパターンを見分けよう!
- 電車の先頭が動いた距離を考えて道のりを算出しよう!
- 単位(秒速・分速・時速,cm・m・km)に気をつけて回答しよう!
終わりに
今回は通過算の攻略法の基礎についてご紹介してきました。実際の入試では,文章の構造が複雑だったりグラフが登場したりと,これらの例題より難しい問題が登場してくることでしょう。それでも基本的な解き方や考え方の部分は変わりません。基本を十分に理解できたな,と思われた方はおすすめ記事や参考書籍を活用しながら,更なる学力向上に励んでいきましょう。