今回は、「和差算」の解き方について解説していきます。
基本から丁寧に学んでいくので、苦手な人もぜひ参考にしてみてください。
Contents
和差算とは
和差算は簡単な四則演算(足し算、引き算、掛け算、割り算)のみで解けるため、中学受験では小学校4年生で習うことが多いです。
一番基本的な形は、ある2つの数量、例えばAとBに対してその和と差が与えられていて、AとBの値を求めるという形です。
これでは分かりにくいと思うので、実際の問題を見てみましょう。
-
りんごとみかんが全部で25個あります。りんごの方がみかんより3個多いです。りんごとみかんはそれぞれいくつありますか?
-
兄と弟が持っているお金の合計は1200円で、兄は弟より300円多く持っています。兄が持っているお金は何円ですか。
-
春子さん、夏子さん、秋子さんの3人で栗(くり)拾いをしました。夏子さんは春子さんの2倍より7個多く、秋子さんは春子さんの3倍より5個少なく拾ったところ、3人の合計が80個になりました。このとき、春子さんは何個拾いましたか。
これだと想像がつきやすいのではないでしょうか。これが和差算の基本形です。
問題を解く上で大切なところには色を付けました。赤が和で青が差です。この情報さえあれば問題は解けます。
和差算の解き方
まずは①の問題を実際に解きながら、和差算の解き方について解説していきます。
(問題①)りんごとみかんが全部で25個あります。りんごの方がみかんより3個多いです。りんごとみかんはそれぞれいくつありますか?
このくらいの問題だと、適当に数を当てはめればそのうち答えは出てしまいます。
ただ、それでは難しい問題が解けないので、ここでは難しい問題を解いていく上で応用の利く考え方を3つご紹介します。
線分図で解く(大きいほうに合わせる)
まずは和差算を解く上で基本の「線分図」を使って解いてみましょう。実際に先ほどの問題を解く前に、この問題を考えてみてください。
(問題☆)りんごとみかんは同じ数(差が0)だけあり、全部で30個である。りんごとみかんはいくつありますか?
この問題は、和差算の「差が0」である特殊な場合と考えることができます。これなら和差算がわからない人でも解くことが出来るのではないでしょうか。
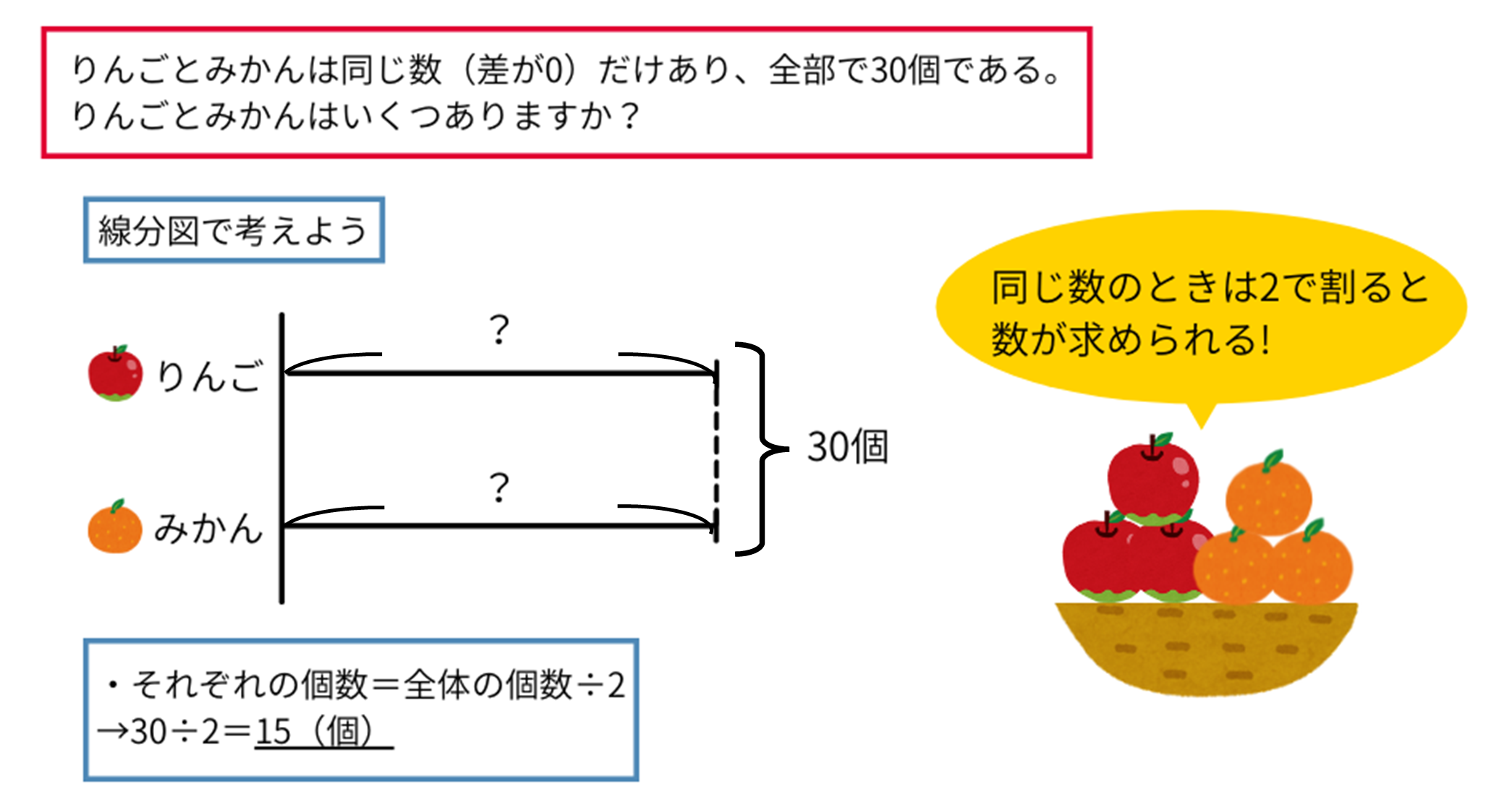
「2種類で同じ数(差が0)だから、それぞれの数は2で割った数になる」ということがわかりましたか?これがわかれば、基本的な和差算はすぐに解けるようになります。
基本を確認したところで、最初の問題①を解いてみましょう。
(問題①)りんごとみかんが全部で25個あります。りんごの方がみかんより3個多いです。りんごとみかんはそれぞれいくつありますか?
できそうな方は、まず自分で解き方を考えてみてください。大事なポイントは、先ほどの問題☆のように「差が0」の状態にすることです。
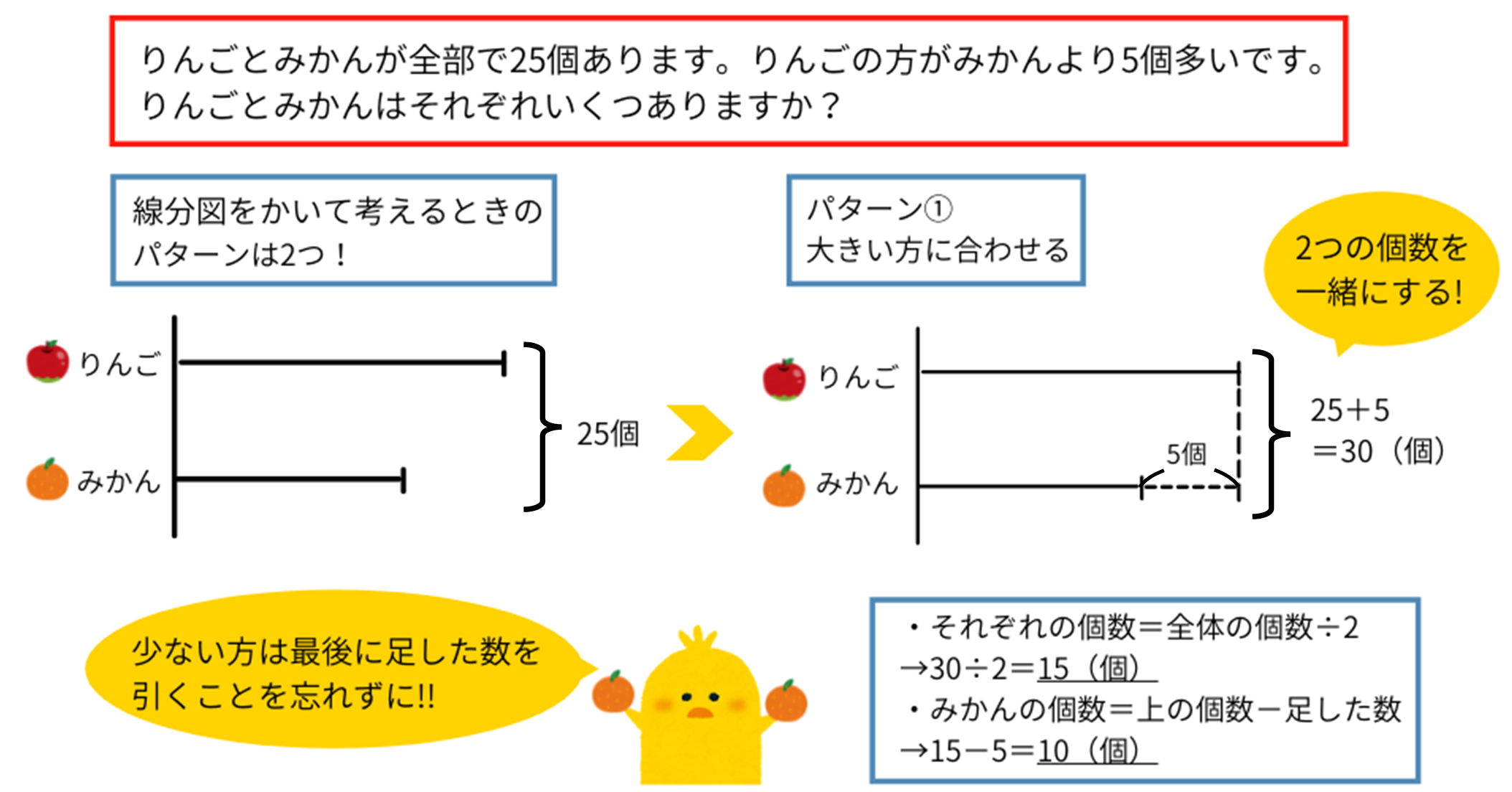
線分図を使った解き方は2パターンありますが、まずは「大きい方に合わせる」解き方で解説していきます。
和差算では、先ほど解いた問題☆のように「差が0」の状態にすれば簡単に求められるので、まずは数を足したり引いたりして同じ数に揃えます。
今回は、少ない方(みかん)を多い方(りんご)と同じ数にするために、みかんを5個分足します。このとき全体の合計の数にも5個足します。
すると、りんごとみかんの個数が同じ数になるので、先ほど解いた問題☆と同じ形になります。あとは合計を2で割れば個数が求まる…のですが、ここで途中で足したみかんの個数を引きます。
自分で数を変えるときは、「合計の数も変わる」「最後の答えは足した分・引いた分を戻す」ということを忘れないようにしましょう。
答えは、りんごが\(30\div2=15\)(個)、みかんが\(15-5=10\)(個)、となります。
最後に、これが本当に問題文の条件を満たすか確かめてみましょう。りんごとみかんの数は\(15+10=25\)(個)、その差は\(15-10=5\)(個)で確かに問題文を満たしていることがわかります。
和差算はすぐ確認できるので、難しい問題に備えて普段から確認するようにしてみるといいかもしれませんね。
線分図で解く(小さいほうに合わせる)
続いては、線分図を使った解き方の2パターン目、「小さい方に合わせる」解き方をご紹介します。この解き方は、先ほど解説した「大きい方に合わせる」やり方がわかれば簡単にわかります。
実際に同じ問題で見てみましょう。先ほど自分で解いて、解説と違うな…と思った方はこちらで解いているかもしれません。
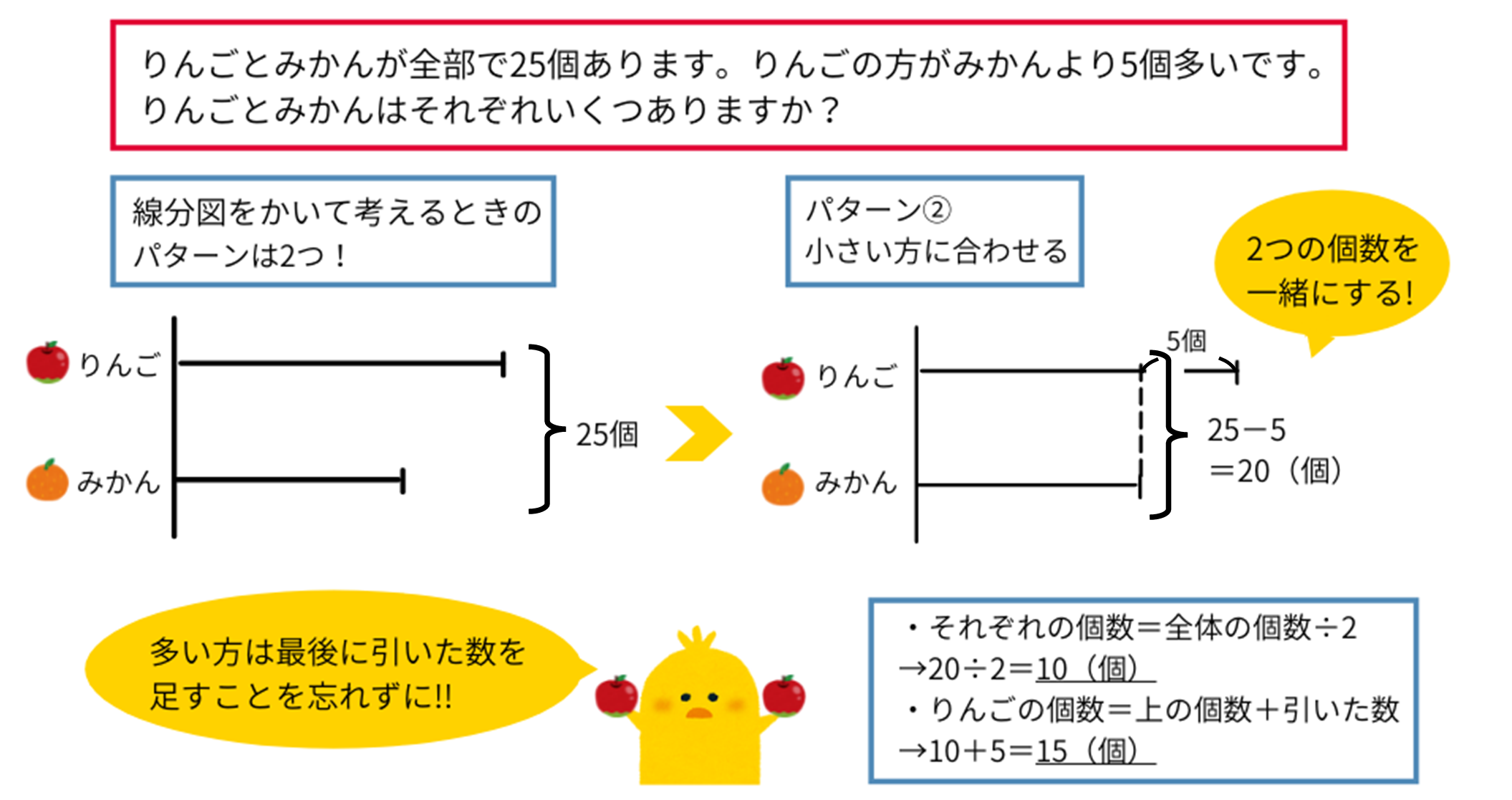
先ほどとは違って、今回は多い方(りんご)を少ない方(みかん)と同じ数にするために、りんごを5個分引きます。このとき全体の合計の数からも5個引きます。
すると、先ほどと数は異なりますが、同じ形になりました。なので、りんごとみかんはそれぞれ10個ずつだと…思いませんよね!前で学んだように、引いた5個のりんごを付け加えてあげる必要があります。
よって答えは、みかんが\(20\div2=10\)(個)、りんごが\(10+5=15\)(個)、となります。
練習問題
これで線分図での解き方の基本は説明できたので、練習問題を解いて慣れていきましょう。線分図で大きい方に合わせるか、小さい方に合わせるかはやりやすい方で大丈夫です。
(問題)兄と弟が持っているお金の合計は1200円で、兄は弟より300円多く持っています。兄が持っているお金は何円ですか。
解説
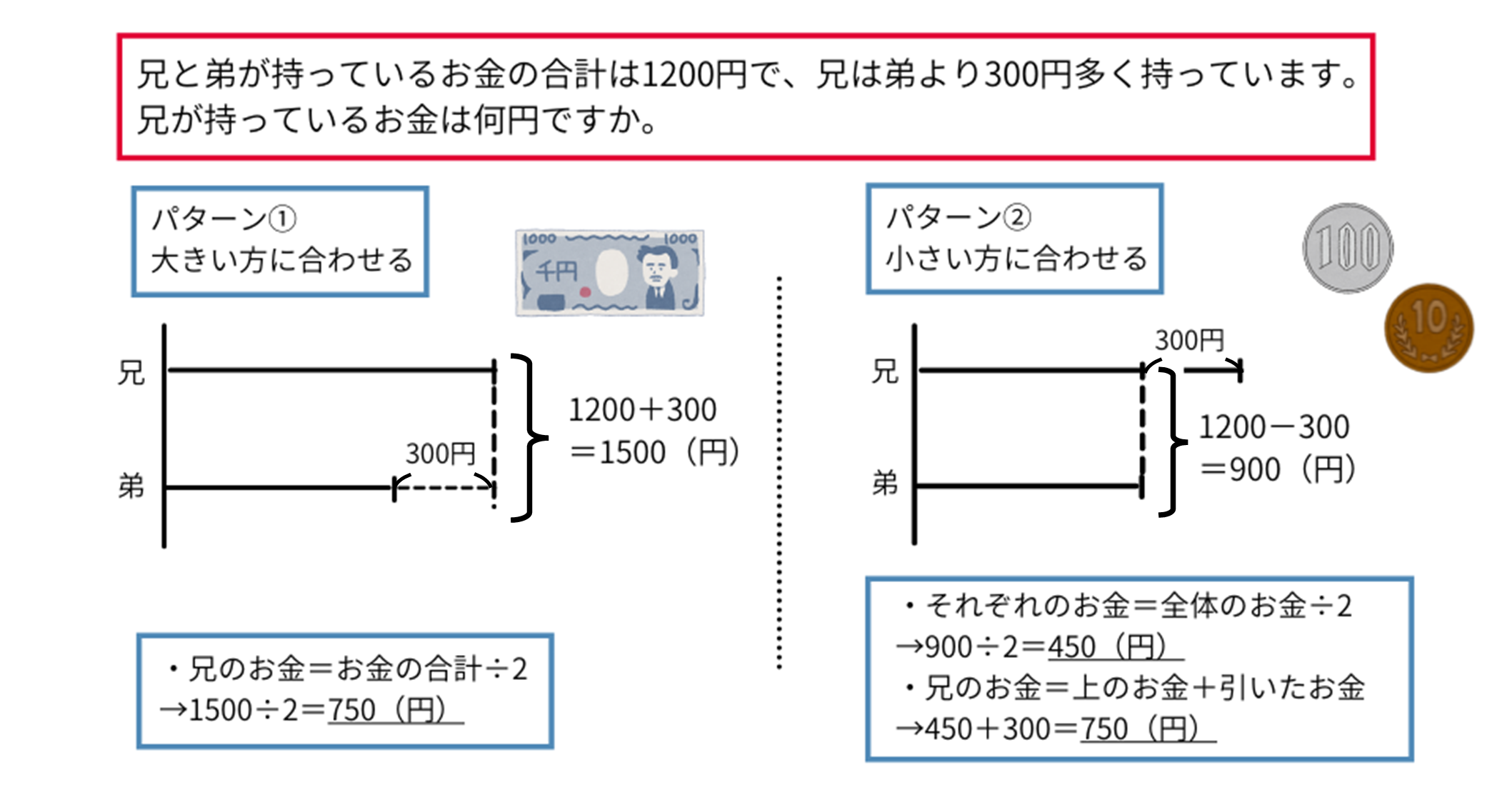
【大きい方に合わせる解き方】
少ない方(弟)を多い方(兄)と同じ金額にするために、弟に300円分足します。このとき全体の合計の数にも300円足します。
兄と弟のお金が同じ数になるので、合計を2で割ればそれぞれのお金が求まります(\(1500\div2=750\))。兄はそのままのお金、弟は足した分を引いた数になります(\(750-300=450\))。
問われているのは兄のお金なので、答えは750(円)です。
【小さい方に合わせる解き方】
多い方(兄)を少ない方(弟)と同じ金額にするために、兄から300円分引きます。このとき全体の合計の数からも300円引きます。
兄と弟のお金が同じ数になるので、合計を2で割ればそれぞれのお金が求まります(\(900\div2=450\))。弟はそのままのお金、兄は引いた分を足した数になります(\(450+300=750\))。
問われているのは兄のお金なので、答えは750(円)です。
まとめ……の前に
『個別指導塾テスティー』の公式LINEにて、 『中学受験を9割成功に導く』メールマガジンを 毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓

まとめ
最後に、基本の線分図での解き方をまとめておきます。
【線分図の解き方】
- 線分図を書く
- 「少ないほうに足す」または「多いほうから引く」ことで2つの数を合わせる
- 2で割ることで片方の数がわかる
- 差の情報からもう片方の数もわかる
和差算が苦手な人も、簡単な問題や似た問題をどんどん解いて得意になってもらえたら嬉しいです。

















