中学入試に臨むにあたって,ある程度過去問を見たり比べたりして傾向を掴むということが重要です。それは,もちろんどんな問題が出てきても対応できる力を身につけることも大事ですが,傾向を掴むことで合格に向けた勉強が効率よくできるからです。
しかしいろんな中学校の問題を比べることは容易ではありません。そこで本記事では,みなさまの受験合格への手助けのため,2021年度の入試傾向をご紹介していきます。今回は様々な中学校のうち偏差値65以上の難関校に焦点を当て,よく出てきた問題とその対策をご紹介していきます。
Contents
1つ目の出題傾向:分数の割り算
まず一つ目にご紹介する出題の特徴は,分数の割り算が含まれた四則演算です。ほとんどの中学校が算数の試験において,一番初めの問題に簡単な計算を出してきます。その目的は早くて正確な計算力を確かめるためだったり,準備体操のような意味合いで頭を算数モードに切り替えるためだったりするのですが,今年度は計算の中に分数の割り算が含まれることが多い印象でした。以下はその例になります。
次の□にあてはまる数を求めなさい。
\((□÷30-1.625)\div\frac{132}{224}-2\frac{7}{9}\times0.1=\frac{1}{2}\)
(聖光学院中学校(2021),一部改題)
次の計算をしなさい。
\(1\frac{5}{8}÷\frac{13}{14}-(0.8\div\frac{4}{3}-\frac{4}{15})\)
(フェリス女学院中学校(2021),一部改題)
上の2つの問題にはどちらも分数の割り算が含まれていました。またそれだけではなく,当然のように帯分数・分子分母が3けたである分数・第3位まである小数なども登場していることにも注意が必要です。
ただしこのような複雑な四則演算は,今年だけでなく難関校であれば例年出題されがちです。小問集合で出されるのは落としたらマズい問題ばかりであり,つまり他の標準的な小学6年生は解けないけどウチを受けるなら解けるよね?というレベルの問題が多いのです。そのため受験校のレベルが高いほど四則演算をはじめとするルールがシンプルな問題は極力難しくされて出題されるのです。
分数の割り算の対策法は?
ではこのような複雑な四則演算に対応するために,どのような演習を積んでいけば良いのでしょうか。その対策法を以下でご説明します。
まずは計算のルールを正確に覚えることが重要になってきます。覚えなければいけないルールはシンプルです。+・-・×・÷という計算記号の意味はもちろんのこと,()の中を計算し,その次に×・÷を計算,そして左から足しひきをしていくという計算の順序なども重要です。分数の割り算に着目するならば,その分数の逆数をかけてあげるということは忘れないでおきたいです。
ただこれくらいなら中学受験を目指されるお子様は理解されていることでしょう。しかしそれだけでなく,中かっこ{}・大かっこ[]のような普段見ない記号の理解も大事になってきます。これらは()の中の計算より先に計算するというマークになります。このような一般的でないルールにも慣れていきましょう。
この慣れのために必要なのが反復演習です。他の単元と違って四則演算はどんなに難しい問題でも基礎に則っていけば解けますので,次々に問題に触れていくことで算数が苦手でも徐々に成長していくでしょう。
またこの反復演習は計算の速度を上げるためにも重要です。複雑な計算を早く解くことができればその分余った時間を他の問題に割くことができます。繰り返しの演習でルールに慣れることで,「どう計算すればいいのだろう」と悩む時間も次第に減っていきます。この点でも分数の割り算,ひいては複雑な四則演算に対して反復演習は有効にはたらきます。
2つ目の出題傾向:速さについての問題
2点目に挙げられる傾向が,速さについての問題です。速さについての問題は中学受験においては定番であり,旅人算・流水算・通過算など様々なものが出題されてきましたが,今年は特にこの分野からの出題が多い印象でした。例えば次のような問題が当てはまります。
長さ56mの船Aと長さ28mの船Bがあります。船Aと船Bがどちらも川を登っているとき,船Bが船Aに追いついてから完全に追い越すまで1分10秒かかりました。また,船Aが川を上り,船Bが川を下っているとき,船Aと船Bが出会ってから完全に離れるまで10.5秒かかりました。次の①,②に答えなさい。
- ①船Aの静水での速さは秒速何mですか。
- ②船Aで川下から川上まで上りましたが,川の流れの速さがいつもの2倍だったので,かかった時間が\(1\frac{3}{11}\)になりました。いつもの川の流れの速さは秒速何mですか。
(早稲田実業学校中等部(2021),一部改題)
A君は自転車に乗ってP駅を出発し,線路沿いの道を一定の速さでQ駅に向かいました。A君がP駅を出発してから3分後に,電車がP駅を出発してQ駅に向かいました。電車がA君の4倍の速さでP駅とQ駅の間を何回か行ったり来たりし,各駅に着くと5分間停車するものとします。
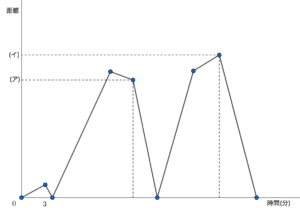
図のグラフは,A君がP駅を出発してからQ駅にたどり着くまでの時間とA君と電車との間の距離の関係を表したものです。このとき,後の問いに答えなさい。
ただし,線路や道は一直線で,道の幅や自転車,電車の長さは考えないこととします。
- (1)A君が電車に初めて後ろから追い越されるのは,A君がP駅を出発してから何分後ですか。
- (2)A君がQ駅にたどり着いたのは,A君がP駅を出発してから何分後ですか。
- (3)A君が電車と初めて正面から出会うのは,A君がP駅を出発してから何分何秒後ですか。
- (4)図の①に当てはまる数と②に当てはまる数の比を求めなさい。
(浅野中学校(2021),一部改題)
この問題は川の流れる速さと船が動く速さの両方を考えていく流水算,そして速い方が遅い方に追い越される通過算というものですが,他にも旅人算が聖光学院中学校で,流水算がフェリス女学院で出題されていました。
難関校の受験において長い文章題は出題されがちですが,その中でもこのような速さの問題は条件や数字がややこしいことが多いです。そのため速さの問題に特化した対策や練習が必要になります。
速さについての問題の対策法は?
それではどのようにして対処していけば良いのでしょうか。
対策法としては,図を書く練習をすることが挙げられるでしょう。速さの問題に限らず中学受験で長い文章題が登場しやすいのは先ほど述べた通りですが,この複雑な条件を整理しなければ問題を解くことはできません。その整理の手段として図を書いてまとめると,内容が理解しやすいといったことは多々あります。例えば1問目の「どちらも川を登っているとき,船Bが船Aに追いついてから完全に追い越すまで1分10秒かかった」という指示をわかりやすくするために図に書くと,次のようになります。
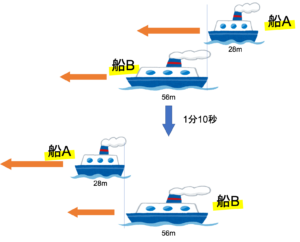
文章だけだとわかりづらいことでも,図に書き起こすと1分10秒の間に船Aが56+28=84m進んだことが明らかになりましたね。またこの84m進んだというのも,実際は船Aも船Bも川を上っているため見かけ上の距離であることもわかりやすくなりました。このように図表に問題を整理するテクニックを身につけるように励むことが攻略につながるでしょう。
加えて条件の整理という意味ではグラフの読み解きも重要になってきます。初めに引用した問題でもグラフが出てきていましたが,このグラフにおける点は何を指すのか,右下がり・右上がりはどういう意味なのか,といった解釈ができるかどうかが答えを導けるかを左右するため,設問に取り掛かる前にグラフを分析することも重要です。
またこれらに加えて道のり・速さ・時間という数字に注目しておくことも速さの問題を特にあたって重要となります。み・は・じの図を常に意識しながら,わからない部分はどこだろうか・逆にどこがわかっているのだろうかを考えながら計算していきましょう。
3つ目の出題傾向:立体を切断する問題
最後にご紹介する傾向の特徴は,立体を切断する問題です。空間図形の問題も中学受験では出題されやすいですが,難関校はその中でも純粋な立方体や直方体ではなく,切ったり組み合わせたりされて一癖も二癖もある図形が特によく出る印象です。2021年度は次のような問題が出されていました。
一片が6cmの立方体ABCD-EFGHがあり,辺ADの真ん中の点をM,変BCの真ん中の点をNとします。この立方体を,3点B,D,Gを通る平面で切断すると,この立法体は6つに分かれます。このうち編AMを含む立体Xについて次の問いに答えなさい。
(聖光学院中学校(2021),一部改題・省略)
1辺の長さが6cmの立方体ABCD-EFGHがあります。直線AFとBEが交わってできる点をP,直線BGと直線CFが交わってできる点をQとします。次の①,②にあてはまる数をそれぞれ求めなさい。
三角すいDEGHの表面積は,三角すいBFPQの表面積の2倍より ① cm2大きいです。また,三角錐DEGHの体積は,三角すいBFPQの体積の ② 倍です。
(フェリス女学院中学校(2021),一部改題・省略)
これらの図形はどれもシンプルな立方体をいじる問題ですが,その分け方が全く違っていることは一目瞭然です。また2問目に関してはただの切断ではなく,そこから図形を展開する必要もある複雑な問題です。そのためどんな問題が来ても対応できるように,柔軟な力を伸ばしていく必要があります。
空間図形の対策法は?
それではどのように空間図形の対策を行なっていけばいいのでしょうか。前述したような柔軟な適応能力を身につけるためには,平面で与えられた情報と空間上の図形のイメージを結びつける練習が必要です。
そのために重要なことの一つ目が,頭の中に空間図形をイメージすることになります。先程の問題であれば,直線を引いたらどのあたりで交わりそうか,切断したらどのような図形ができるかをなんとなく思い浮かべることで,初めて正確な答えを導けます。この発想力の訓練はなかなか難しいですが,以前別の記事でご紹介した究極の立体などのアプリを使うことで,平面のテキストでは補いきれない三次元のイメージが身に付きやすくなります。ぜひ参考にしてみてください。
またこうして頭の中に描けたイメージを平面に落とし込むことも大事になってきます。皆さんは立方体・直方体・角錐などの立体を平面上に書くことができるでしょうか。奥にあるものを点線で書いて,上面と下面を同じ形で描いて,・・・という流れで立体を描いていくのが定番ですが,このような立体の描き方について習う機会はあまり多くないのではないかと思われます。
そのため頭の中の図形を平面上に表すために,立体の描き方を押さえておくことが大事です。このような知識を身につけるためには,演習問題を積み重ねることも大事ですが,基本的な問題に付属している図形を見ながら移していくことも有効です。よろしければ参考にしてみてください。
まとめ
今回は2021年度入試の難関校の問題を眺め,その傾向や対策法についてまとめていくものでした。以下はその要約になります。
- 分数の割り算を含む複雑な計算という傾向→反復演習で対策!
- 速さについての問題という傾向→図表を読み解く・図表にまとめる練習で対策!
- 立体の切断という傾向→空間のイメージ・平面への落とし込みを練習して対策!
ここで述べた傾向は一部のものでありますが,この3点のように複雑な問題は例年出題されやすいものですので,対策は必須かと思われます。
ただ,もちろん滑り止めとして下のレベル帯の学校も受験されるご家庭や,このような難関校以外の中学校を志望されるお子様がいるご家庭もあると思われます。そのような場合には別日に投稿される【標準校編】の記事などを参考にしていただけたらと思います。本記事が学習の手助けとなれば幸いです。