皆さんは「熱の移動と温度変化」に関する入試問題の過去問題を解いたことがあるでしょうか? 「熱の移動と温度変化」は中学受験理科では頻出の分野とはいえませんが、実際に出題された例もあり、対策なしには解くことはできません。今回は、カロリー計算などの問題について、実際に出題された入試問題を解説します! 「熱の移動と温度変化」に関してまだ基礎がわかっていない……という人は過去の記事で解説しているので参考にしてください! これらの予備知識がなくても解説では丁寧に知識の復習もおこないますので、実際に出題された問題の解説を理解しながら学習してもよいでしょう。
それでは早速解説していきます!
世田谷学園中学校 2013年
問題
次の文を読んで、あとの問いに答えなさい。
コップの水に氷を入れると冷たい水ができます。これは水と氷との間で熱のやりとりをするからです。このことについて考えてみましょう。
氷の温度は\(0\,{}^\circ\mathrm{C}\)よりも低いので、\(0\,{}^\circ\mathrm{C}\)よりも低い温度を表す必要性があります。このときに、「マイナス~℃」のような言葉を使います。例えば、\(0\,{}^\circ\mathrm{C}\)よりも\(5\,{}^\circ\mathrm{C}\)だけ低い温度を表すときには「マイナス\(5\,{}^\circ\mathrm{C}\)」となります。
下のグラフは、ビーカー内のマイナス\(20\,{}^\circ\mathrm{C}\)の氷に一定の割合で熱を加え続けたときの、時間と温度の関係を表しています。
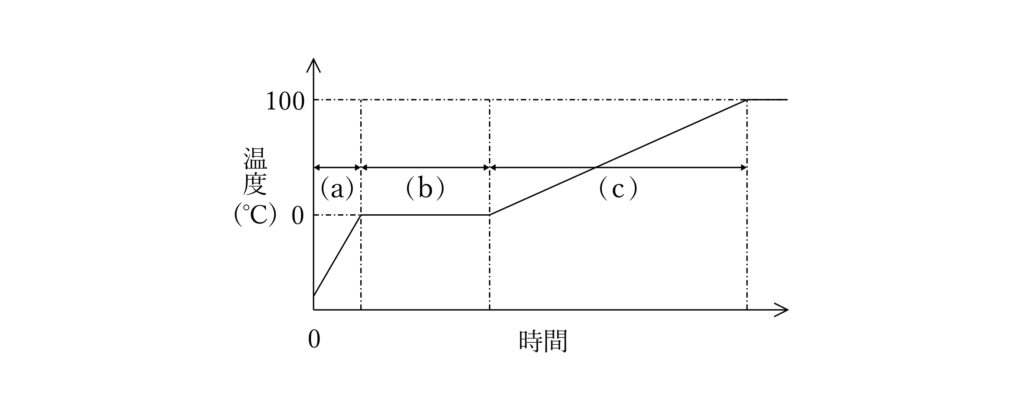
グラフの(c)のときには、ビーカー内は水しかありません。\(1\,\mathrm{g}\)の水の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を\(1\)カロリーといいます。グラフの(b)のときには、ビーカー内の温度は\(0\,{}^\circ\mathrm{C}\)のままです。これは加えているすべての熱が、氷をとかすのに使われているからです。このとき、\(0\,{}^\circ\mathrm{C}\)、\(1\,\mathrm{g}\)の氷を\(0\,{}^\circ\mathrm{C}\)、\(1\,\mathrm{g}\)の水に変化させるのに必要な熱量を\(80\)カロリーとします。グラフの(a)のときには、ビーカー内は氷しかありません。このとき、\(1\,\mathrm{g}\)の氷の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を\(0.5\)カロリーとします。
すべての熱は水もしくは氷とのやりとりのみに使われ、ビーカーや空気中にはにげないものとします。
問1 ビーカー内の水\(240\,\mathrm{g}\)の温度を、\(40\,{}^\circ\mathrm{C}\)から\(84\,{}^\circ\mathrm{C}\)にするのに必要な熱量は何カロリーですか。
解説
この問題は、問題文の中にヒントがあります。それは
\(1\,\mathrm{g}\)の水の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を\(1\)カロリーといいます
という部分です。これがあれば、予備知識がなくても解けるようになっています。
ここで、「カロリーと熱量にはどのような関係があるの?」と疑問に思った人もいるかもしれません。「カロリー」とは「熱量」の単位のことです。「熱量」と「エネルギー」はほぼ同じ意味なので、「カロリー」は「エネルギー」の単位ということもできます。通常、エネルギーの単位には\(\mathrm{J}\)(ジュール)が使われますが、カロリーは水\(1\,\mathrm{g}\)、\(1\,{}^\circ\mathrm{C}\)のエネルギーに対応していますので、水などをあつかうときはカロリーという単位を用いた方が便利なのです。ちょうど、体積の単位で\(\mathrm{L}\)(リットル)や\(\mathrm{m^3}\)(立方メートル)を使い分けるのと同じですね。
いま、水は\(240\,\mathrm{g}\)で、\(40\,{}^\circ\mathrm{C}\)から\(84\,{}^\circ\mathrm{C}\)にしたいので、
\(240\,\mathrm{g} \times (84\,{}^\circ\mathrm{C} – 40\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C} = 10560\,\mathrm{cal}\)
となります。
ここで、\(1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}\)と書いてあるのは問題文で与えられたカロリーの定義によって決まる値で、単位をそろえるために式に含めています。省略される場合がほとんどですが、本記事では表記することにします。ちなみに、ある物質\(1\,\mathrm{g}\)の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を表わしたものを「比熱」とよびます。\(1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}\)は水の比熱です。
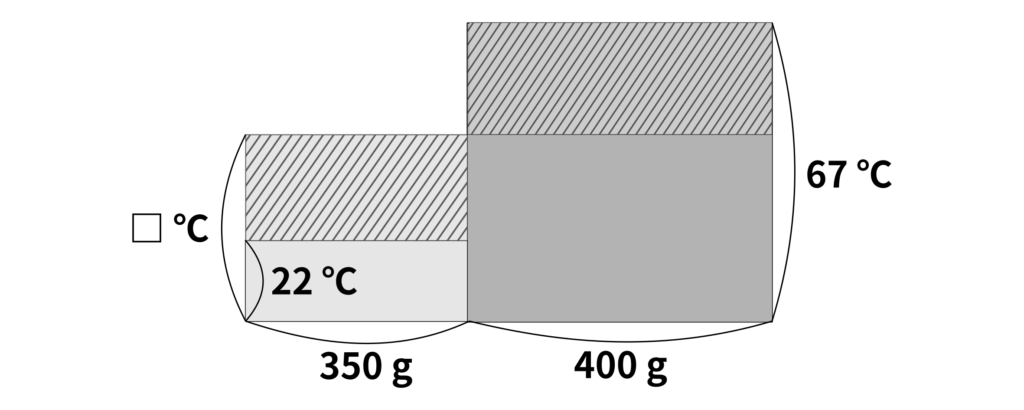
問2 ビーカーAには\(22\,{}^\circ\mathrm{C}\)の水が\(350\,\mathrm{g}\)、ビーカーBには\(67\,{}^\circ\mathrm{C}\)の水が\(400\,\mathrm{g}\)入っています。ビーカーAの水をすべてビーカーBに移したところ、一定の温度になりました。このとき、ビーカーBの水の温度は何\(\,{}^\circ\mathrm{C}\)ですか。
解説
この問題は、2つの物体同士の熱の移動をあつかっています。このとき、
(物体Aが失った熱量)=(物体Bが得た熱量)
という関係を頭に入れておきましょう。温度一定になったときのビーカーBの温度を□\(\,{}^\circ\mathrm{C}\)としましょう。このとき、水の量を温度の関係は次の面積図で表わせます。
ビーカーA、ビーカーBそれぞれの水について移動した熱量を計算すると、
ビーカーA……\(350\,\mathrm{g}\times (\text{□}\,{}^\circ\mathrm{C}-22\,{}^\circ\mathrm{C})\times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}=350\times (\text{□}-22)\,\mathrm{cal}\)
ビーカーB……\(4000\,\mathrm{g}\times (67\,{}^\circ\mathrm{C}-\text{□}\,{}^\circ\mathrm{C})\times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}=400\times (67-\text{□})\,\mathrm{cal}\)
となります。したがって、温度一定になったあとのビーカーBの水の温度は
\(46\,{}^\circ\mathrm{C}\)
と求めることができます。
問題3 ビーカー内の-\(16\,{}^\circ\mathrm{C}\)の氷\(130\,\mathrm{g}\)に\(15600\)カロリーの熱量を加えたところ、ビーカー内の氷はすべてとけて水だけになりました。ビーカー内の水の温度は何\(\,{}^\circ\mathrm{C}\)ですか。
解説
この問題は、次の流れで解いてきます。
- 氷を\(0\,{}^\circ\mathrm{C}\)にするのにどれくらいの熱量が必要なのかを計算する……①
- \(0\,{}^\circ\mathrm{C}\)の氷をすべて\(0\,{}^\circ\mathrm{C}\)の水に変えるのに必要な熱量を計算する……②
- 与えられた熱量から、氷を\(0\,{}^\circ\mathrm{C}\)の水に変化させるまでに使ったすべての熱量(①+②)を引く……③
- ③の熱量が、\(0\,{}^\circ\mathrm{C}\)の水をさらに温めるのに使われる熱量なので、これから最終的な水の温度を計算する
まず、マイナス\(16\,度\)の氷を\(0\,{}^\circ\mathrm{C}\)の氷にするのに必要な熱量を計算しましょう。問題文より、
\(1\,\mathrm{g}\)の氷の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を\(0.5\)カロリーとします
とあるので、\(130\,\mathrm{g}\)、マイナス\(16\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)にするのに必要な熱量は
\(130\,\mathrm{g}\times 16\,{}^\circ\mathrm{C}\times 0.5\,\mathrm{cal}\,/\,\mathrm{g}=1040\,\mathrm{cal}\)
となります。
次に、\(0\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)の水に変化させるのに必要な熱量を計算しましょう。問題文より、
\(0\,{}^\circ\mathrm{C}\)、\(1\,\mathrm{g}\)の氷を\(0\,{}^\circ\mathrm{C}\)、\(1\,\mathrm{g}\)の水に変化させるのに必要な熱量を\(80\)カロリーとします
とあるので、氷\(130\,\mathrm{g}\)をとかすのに必要な熱量は
\(130\,\mathrm{g}\times 80\,\mathrm{cal}\,/\,\mathrm{g}=10400\,\mathrm{cal}\)
となります。
このとき、余っている熱量は
\(15600\,\mathrm{cal} – 1040\,\mathrm{cal} – 10400\,\mathrm{cal} = 4160\,\mathrm{cal}\)
となります。これが\(0\,{}^\circ\mathrm{C}\)の水を温めるのに使われる熱量なので、最終的なビーカー内の水の温度を□\(\,\mathrm{度}\)とすると、
\(130\,\mathrm{g} \times (\text{□}\,{}^\circ\mathrm{C} – 0\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C} = 4160\,\mathrm{cal} \)
となるので、
\(32\,{}^\circ\mathrm{C}\)
と求めることができます。
問4 ビーカー内のマイナス\(20\,{}^\circ\mathrm{C}\)の氷\(270\,\mathrm{g}\)に\(1\)秒間あたり\(170\)カロリーの熱量を加え続けたところ、ビーカー内の氷はずべてとけて\(46\,{}^\circ\mathrm{C}\)の氷だけになりました。熱量を加えた時間は何分何秒ですか。
解説
この問題も、途中までは先ほどの問題と同じ解き方です。次の流れで解いてきます。
- 氷を\(0\,{}^\circ\mathrm{C}\)にするのにどれくらいの熱量が必要なのかを計算する……①
- \(0\,{}^\circ\mathrm{C}\)の氷をすべて\(0\,{}^\circ\mathrm{C}\)の水に変えるのに必要な熱量を計算する……②
- \(0\,{}^\circ\mathrm{C}\)の水を\(46\,{}^\circ\mathrm{C}\)の水に変えるのに必要な熱量を計算する……③
- (①+②+③)の熱量が、ビーカー内のマイナス\(20\,{}^\circ\mathrm{C}\)の氷を\(46\,{}^\circ\mathrm{C}\)の水に変えるのに必要な熱量である
- (①+②+③)の熱量を加えるのに必要な時間を計算する
まず、マイナス\(20\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)の氷にするのに必要な熱量を計算しましょう。問3と同様に、\(270\,\mathrm{g}\)、マイナス\(20\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)にするのに必要な熱量は
\(270\,\mathrm{g}\times 20\,{}^\circ\mathrm{C}\times 0.5\,\mathrm{cal}\,/\,\mathrm{g}=2700\,\mathrm{cal}\)
となります。
次に、\(0\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)の水に変化させるのに必要な熱量を計算しましょう。氷\(270\,\mathrm{g}\)をとかすのに必要な熱量は
\(270\,\mathrm{g}\times 80\,\mathrm{cal}\,/\,\mathrm{g}=21600\,\mathrm{cal}\)
となります。
次に、\(0\,{}^\circ\mathrm{C}\)の水を\(46\,{}^\circ\mathrm{C}\)の水に変化させるのに必要な熱量を計算しましょう。水を温めるのに必要な熱量は
\(270\,\mathrm{g}\times 46\,{}^\circ\mathrm{C}\times 80\,\mathrm{cal}\,/\,\mathrm{g}=21600\,\mathrm{cal}\)
となります。
したがって、必要な熱量を合計すると
\(2700\,\mathrm{cal} + 21600\,\mathrm{cal} + 12420\,\mathrm{cal} = 36720\,\mathrm{cal}\)
となります。1秒間あたり、\(170\)カロリーの熱量を加えるので、必要な時間は
\(36720 \div 170 \,\mathrm{cal}\,/\,\text{秒} = 216\,\text{秒} = 3\,\mathrm{分}\,36\,\text{秒}\)
と求めることができます。
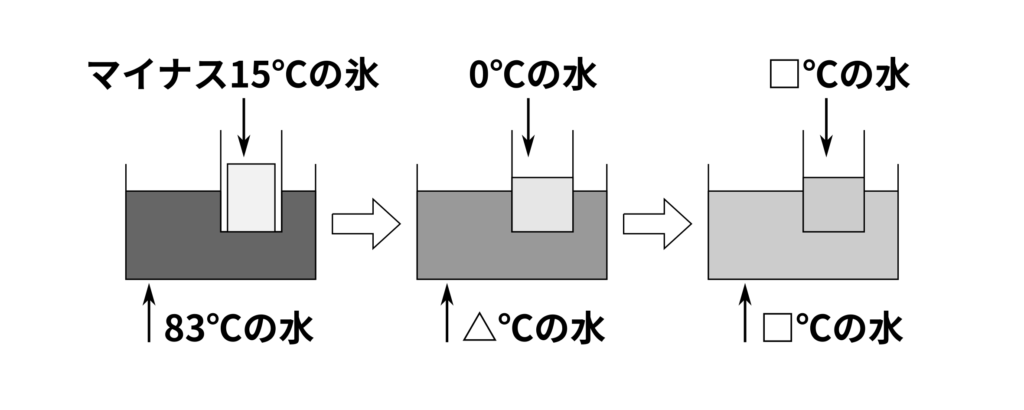
問5 ビーカーCにはマイナス\(15\,{}^\circ\mathrm{C}\)の氷が\(180\,\mathrm{g}\)、ビーカーDには\(83\,{}^\circ\mathrm{C}\)の水が\(315\,\mathrm{g}\)入っています。ビーカーCの氷をすべてビーカーDに移して十分時間がたったとき、移した氷はすべてとけてビーカーDは水だけになり、一定の温度になりました。このとき、ビーカーDの水の温度は何\(\,{}^\circ\mathrm{C}\)ですか。
解説
この問題は、次の流れで解いてきます。
- 氷を\(0\,{}^\circ\mathrm{C}\)にするのにどれくらいの熱量が必要なのかを計算する……①
- \(0\,{}^\circ\mathrm{C}\)の氷をすべて\(0\,{}^\circ\mathrm{C}\)の水に変えるのに必要な熱量を計算する……②
- (①+②)の熱量を与えたビーカーDの水が\(83\,{}^\circ\mathrm{C}\)から何\(\,{}^\circ\mathrm{C}\)になったかを計算する……③
- 問2と同様に、\(0\,{}^\circ\mathrm{C}\)の水を③で求めた温度の水に加え、一定の温度になったときの温度を計算する
一度に考えると複雑なので、順番に考えましょう。ビーカーCの氷はビーカーDの中にあった水から熱量を受けとり、温度一定の状態になります。これを、ビーカーCの氷が\(0\,{}^\circ\mathrm{C}\)の水になるまでと、\(0\,{}^\circ\mathrm{C}\)の水が温度一定になるまでにわけて考えます。
まず、マイナス\(15\,度\)の氷を\(0\,{}^\circ\mathrm{C}\)の氷にするのに必要な熱量を計算しましょう。問3と同様に、\(180\,\mathrm{g}\)、マイナス\(15\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)にするのに必要な熱量は
\(180\,\mathrm{g}\times 15\,{}^\circ\mathrm{C}\times 0.5\,\mathrm{cal}\,/\,\mathrm{g}=1350\,\mathrm{cal}\)
となります。
次に、\(0\,{}^\circ\mathrm{C}\)の氷を\(0\,{}^\circ\mathrm{C}\)の水に変化させるのに必要な熱量を計算しましょう。氷\(180\,\mathrm{g}\)をとかすのに必要な熱量は
\(180\,\mathrm{g}\times 80\,\mathrm{cal}\,/\,\mathrm{g}=14400\,\mathrm{cal}\)
となります。
このとき、ビーカーDに入っていた水の温度が△\(\,{}^\circ\mathrm{C}\)になったとします。ここまでに必要な合計の熱量は
\(1350\,\mathrm{cal} + 14400\,\mathrm{cal} = 15750\,\mathrm{cal}\)
と計算できるので、
\(315\,\mathrm{g} \times (83\,{}^\circ\mathrm{C} – \text{△}\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C} = 15750\,\mathrm{cal} \)
より、ビーカーDに入っていた水の温度は
\(33\,{}^\circ\mathrm{C}\)
となります。
次に、\(0\,{}^\circ\mathrm{C}\)の水を\(33\,{}^\circ\mathrm{C}\)の水に加えて温度一定になったときの温度を求めます。問2と同じように、温度一定になったときの温度を□\(\,{}^\circ\mathrm{C}\)として、それぞれのビーカーの移動した熱量を計算すると、
ビーカーC……\(180\,\mathrm{g}\times (\text{□}\,{}^\circ\mathrm{C}-0\,{}^\circ\mathrm{C})\times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}=180\times \text{□}\,\mathrm{cal}\)
ビーカーD……\(315\,\mathrm{g}\times (33\,{}^\circ\mathrm{C}-\text{□}\,{}^\circ\mathrm{C})\times 1\,\mathrm{cal}\,/\,\mathrm{g}\,{}^\circ\mathrm{C}=315\times (33-\text{□})\,\mathrm{cal}\)
となります。したがって、温度一定になったあとのビーカーDの水の温度は
\(22\,{}^\circ\mathrm{C}\)
と求めることができます。
最後に
本記事では、「熱の移動と温度変化」に関する入試問題を解説しました! 水と氷が混ざったときの温度の変化や、氷をとかすために必要な温度について混乱を起こすことなく、答えることができたでしょうか? 一回で解くことができなかったという人も、何度も同じ問題を復習することで、似たような問題にも対処することができます。決して出題頻度が高い分野とはいえませんが、もし出題されたときに差をつけられるように、一つ一つの分野の基礎をマスターしていきましょう! それでは、引き続き受験勉強を頑張ってください!
おすすめ記事
- 熱の移動と温度変化 ~「熱」とは何かを理解し、問題を解きながら基礎を知ろう!~
- 熱の移動と温度変化~熱量とは何かを理解し、カロリー計算に強くなろう!〜
- てこのつり合いのまとめ その1
- てこのつり合いのまとめ その2
- 物理の勉強法~苦手な人への処方箋
- 【中学受験】今だからできる!理科勉強法・克服法 物理編


















