今回のテーマは,整数に関する問題です。ざっくりと説明すると整数とは,小数でも分数でもない数のことをいいます。(中学生以降はもう少し複雑な分類になりますが…)この分野は,あらゆる問題の基礎となる部分です。ここでは,整数問題を解くにあたって必要な基本的な部分をご紹介します。是非この機会に整数の基礎をしっかりと理解して,得意分野にしてしまいましょう!
倍数と約数
まず,倍数とは,ある数を整数倍したものです。次に,約数とは,ある数を余りを出さずに他の整数で割り切ることができる整数です。もう少しわかりやすくするために数式で見てみましょう。
A,B,Cが0ではない整数であるとき, A = B × C において,
- AはB,Cの倍数
- B,CはAの約数
です。
また,公約数とは,2つ以上の整数に共通する約数のことです。最大公約数とは,いくつかある公約数のうち,最も大きい数をいいます。公約数は,最大公約数の約数だともいえます。
同様に,公倍数とは,2つ以上の整数に共通する倍数のことです。そのうち,最も小さい数のことを最小公倍数といいます。公倍数は,最小公倍数の倍数だともいえます。
基本的な例題
[例題の解説]
- (1)2けたの整数について,13の倍数はいくつありますか。
- (2) 87の約数をすべて求めなさい。
- (3) 108と126の公約数をすべて求めなさい。また,最大公約数はいくつですか。
- (4) 12と18の公倍数で,小さい方からかぞえて5番目の数はいくつですか。
- (1) 2けたの整数は99までの数なので,
99 ÷ 13 = 7 あまり 8
これより,2けたの13の倍数は,
13 × 1 = 13,13 × 2 = 26,…,13 × 7 = 91 となる。
よって,2けたの13の倍数は7個。
答え:7個
- (2) 87がどの数で割り切れるかを探し,2つの整数の積で表すと,
87 = 1 × 87 = 3 × 29
これより,87の約数は,1, 3, 29, 87
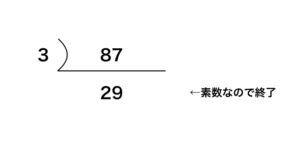
答え:1, 3, 29, 87
- (3) 2数の最大公約数を計算すると, 2 × 3 × 3 = 18
公約数は最大公約数の約数なので,18の約数。
18 = 1 × 18 = 2 × 9 = 3 × 6
これより,18の約数は,1, 2, 3, 6, 9, 18
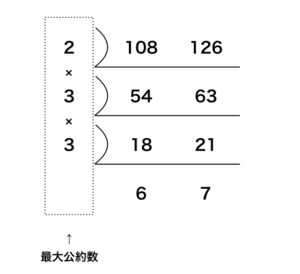
答え:公約数は1, 2, 3, 6, 9, 18 /最大公約数は18
- (4) 12と18の最小公倍数を計算すると,2 × 3 × 2 × 3 = 36
求める数は小さい方からかぞえて5番目の数なので, 36 × 5 = 180
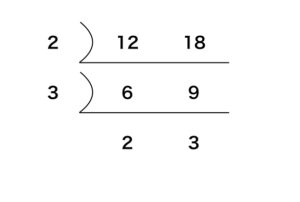
答え:180
素因数分解
まず,因数とはある数を2つ以上の整数の積で表したときの,その数のことをいいます。その中でも素数である因数が素因数です。そして,整数を素因数だけの積で表すことを素因数分解するといいます。
例えば,12の約数は, { 1, 2, 3, 4, 6, 12 } なので,
これより,12 = 1 × 12 = 2 × 6 = 3 × 4 と表せます。
このときの因数は,それぞれ,
- 1 × 12 なら1と12,
- 2 × 6 なら2と6,
- 3 × 4 なら3と4
となります。
また,12を素因数分解すると,12 = 2 × 2 × 3 となります。
この素因数分解を利用して,約数の個数を求めることができます。試しに12の約数の個数を求めてみましょう。
まず,素因数分解した結果から,12は2が2個と3が1個に分解されているので,これらの積の組み合わせで約数が作られます。このとき,2や3が0個のときには1が約数になります。(*20や30が1であるという説明の方が正しいのですが,こちらは中高生の範囲になるため,今回は扱いません。)
例えば,2が0個,3が1個のとき, 1 × 3 = 3
よって,3が約数です。12の約数は,2が最大2個(0〜2個),3が最大1個(0個,1個)をかけてできる整数全体になります。
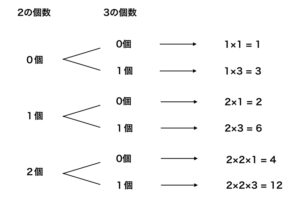
したがって,素因数の選び方は2が0〜2個の3通り,3が0個か1個の2通りなので,12の約数の個数は 3 × 2 = 6 (個) と求められます。(はじめに求めた約数の個数を数えても,合っていることがわかります。 )
このように,全ての組み合わせを考えると約数の個数を求めることができます。
基本的な例題
- (1) 360を素因数分解しなさい。
- (2) 素因数分解を利用して,81と56の約数の個数をそれぞれ求めなさい。
- (3) 80を2でわり続けるとき,何回目で商が整数でなくなるか求めなさい。
- (4) 3 × 6 × 18 を 3でわり続けるとき,何回目で商が整数でなくなるか求めなさい。
[例題の解説]
- (1) 360 = 2 × 2 × 2 × 3 × 3 × 5
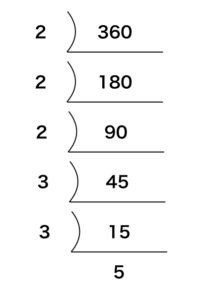
答え:2 × 2 × 2 × 3 × 3 × 5
- (2)
- まず,81の場合,
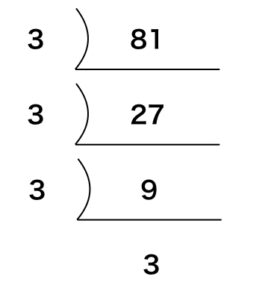
81 = 3 × 3 × 3 × 3
よって,素因数の選び方は,3が0個から4個の5通りなので,81の約数の個数は5個
- まず,81の場合,
-
- 次に,56の約数の個数は,
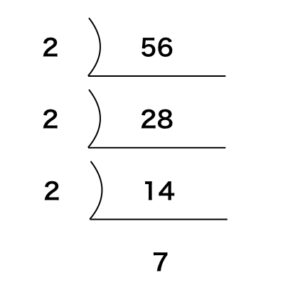
56 = 2 × 2 × 2 × 7
これより,2が3個,7が1個なので, ( 3 + 1 ) × ( 1+ 1 ) = 8
- 次に,56の約数の個数は,
答え:81の約数の個数は5個,56の約数の個数は8個
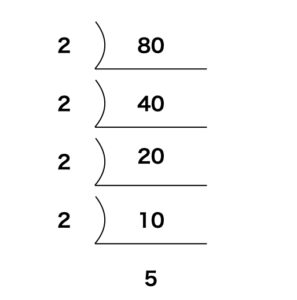
- (3) 80を素因数分解すると,
80 = 2 × 2 × 2 × 2 × 5
これより,80は2を4つふくむので,2で4回割り切ることができます。5は素数なので,5回目の割り算のときに商が小数になり,整数でなくなります。
答え:5回目
- (4) まず,3 × 6 × 18 に 3がいくつ含まれているかを考えてみましょう。
3 = 3 × 1
6 = 3 × 2
18 = 3 × 3 × 2
これより,3 × 6 × 18 = 3 × 3 × 3 × 3 × 2 × 2と変形できるので, 3 × 6 × 18 には 3 が4つふくまれていることがわかる。
よって,5回目の割り算で商は整数でなくなります。
答え:5回目
終わりに
整数問題についての理解は深まりましたか? ここまで読み進めてくださった皆さんは,もう整数に関する問題の基本はばっちり押さえられたのではないでしょうか。パッと素因数分解して素早く解けるようにしちゃいましょう! (特に約数の個数に関しては,単純な書き出しよりも素因数分解を用いた方が素早く確実に答えが出せるので,是非使いこなせるようにしてください。)
おすすめ記事
参考

















