皆さんは「ばねの基本」と聞いてどのようなことを思い浮かべるでしょうか? ばねの練習問題などでは、ばねを直列、並列につないだときのばねの伸びを答えさせる問題などをよく見かけると思います。これらの問題は特徴的なので、よくあるばねの問題だと理解している人も多いと思います。
では、「ばねにかかる力のつり合い」はどうでしょうか? これがばねの問題の基本の一つであることは知っていましたか? おそらく「ばねにかかる力のつり合い」は見落とされがちな内容だと思います。その理由は、直列つなぎや並列つなぎに比べて特徴がなく、視覚的に理解しにくく、説明が難しいといった点にあります。例えば、「ばねが天井から受ける力」なんてものは想像するのも説明するのも難しいですよね。
今回はそんな「ばねにかかる力のつり合い」について解説していきます。単なる「力のつり合い」という単元も存在しますが、それに比べて、ばねの伸びという考えが加わる分、複雑な力学の問題に出題されやすい内容ですので、問題を解きながら段階的に理解していきましょう。まだ「直列つなぎや並列つなぎが理解できていない」、もしくは「忘れてしまった」という人は、以下の過去記事も参考にしてください!
それでは解説に入ります。

ばねにかかる力のつり合い
「ばねにかかる力のつり合い」とは何でしょうか。あまりピンとこない人が多いと思いますので、まずは簡単な場合のつり合いを考えてみましょう。
下の図1を見てください。ばねはおもり\(10\,\mathrm{g}\)あたり\(1\mathrm{cm}\)だけ伸びるものとします。また、ばねの重さは無いものとします。おもりの重さを\(10\,\mathrm{g}\)とすると、ばねがおもりから受ける力は何\(\,\mathrm{g}\)になるでしょうか?(正確には、「重さ」と「力」は違うのですが、同じようなものとして考えます。)また、ばねの伸びは何\(\,\mathrm{cm}\)になるでしょうか?

難しく考える必要はありません。答えは「\(10\,\mathrm{g}\)」です。\(10\,\mathrm{g}\)のおもりをぶら下げたので、当然ですね。また、ばねの伸びは\(1\,\mathrm{cm}\)になります。ここからが本題です。
では、ばねが天井から受ける力は何\(\,\mathrm{g}\)になるでしょうか。
「天井がばねを引く力なん、考えたこともない!」という人もいるかもしれませんが、これは力のつり合いを考えれば簡単にわかります。
いま、ばねはおもりによって\(10\,\mathrm{g}\)の力で下に引っ張られていましたよね。なので、ばねは天井からも\(10\,\mathrm{g}\)の力で上に引っ張られています。なので答えは\(10\,\mathrm{g}\)です。
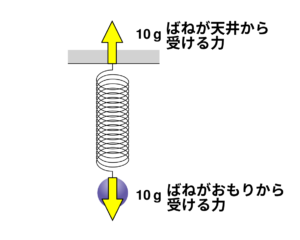
なぜ力がつり合っているのでしょうか? それは、物体が静止しているからです。もし、ばねが天井にぶら下がっていなかったらどうなるでしょうか。この場合、ばねは天井から引っ張られる力を失い、床に落ちてしまいます。つまり、ばねは力の方向に動くのです。一般に、物体にかかる力がつり合っている場合、物体は力の方向に移動します。反対に、物体にかかる力がつり合っている場合、物体は静止しているはずです。この事実をしっかりと認識しておきましょう。このことがわかっていれば、「ばねは静止しているから、ばねはおもりと同じだけの力を天井から受けているはずだ」とすぐに考えることができるでしょう。
このことを踏まえて、次の問題です。
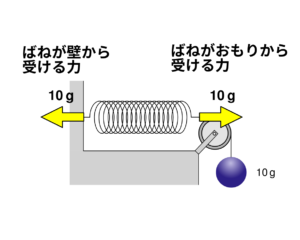
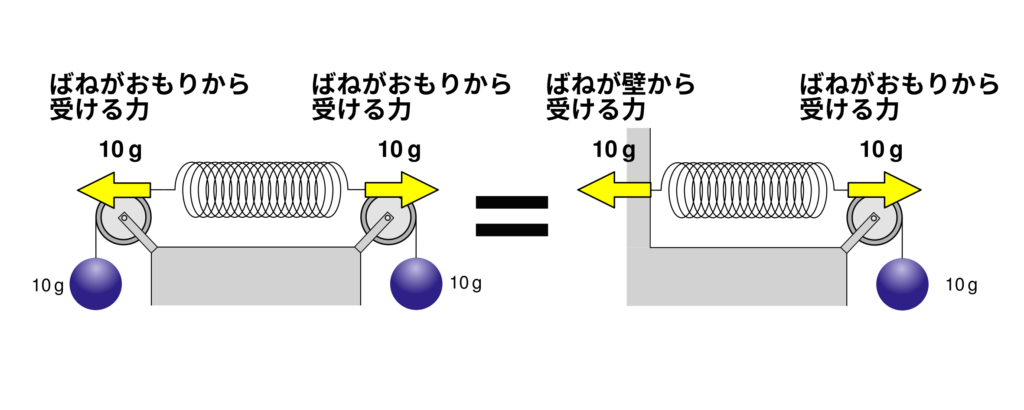
下の図2を見てください。ばねが滑車を通したおもりから受ける力と、壁から受ける力はそれぞれ何\(\,\mathrm{g}\)でしょうか。また、ばねの伸びは何\(\,\mathrm{cm}\)になるでしょうか?
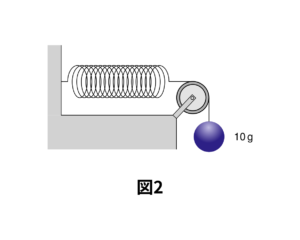
もちろん答えは両方とも「10\(\,\mathrm{g}\)」ですね。ばねがおもりから受ける力は滑車があっても同じです。また、ばねは静止しているので、ばねが壁から受ける力は、おもりから受ける力と同じになります。また、ばねの伸びは\(1\,\mathrm{cm}\)になります。
さて次は、少しややこしい状況について考えてみましょう。
次の図3を見てください。ばねが滑車を通したおもり①と②から受ける力は、それぞれ何\(\,\mathrm{g}\)でしょうか。
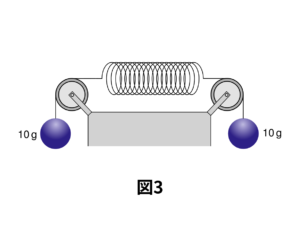
これも今までの問題を見てきた人ならわかると思います。答えは両方とも「10\(\,\mathrm{g}\)」ですね。ばねは両方から同じ力を受けて静止しています。では、同じ状況をばねの伸びはどうなるでしょう。次の問題の答えをよく考えてみてください。
では、ばねの伸びは何\(\,\mathrm{cm}\)になるでしょうか。
おもりが二つあるから答えは「\(2\,\mathrm{cm}\)」と答えた人は、前の問題との違いをよ~く考えてみてください。これまでの問題は「ばねが両側から\(10\,\mathrm{g}\)の力で引っ張られている」状況でしたね。そして、ばねの伸びは\(1\,\mathrm{cm}\)でした。
今回の場合はどうでしょうか。今回も「ばねが両側から\(10\,\mathrm{g}\)の力で引っ張られている」状況ですよね? したがって、ばねにかかる力は前の状況と同じ、つまり、ばねの伸びも同じく「\(1\,\mathrm{cm}\)」になります! それでもわからないという人は片方のおもりに注目して、もう片方を壁に置きかえてしまうといいでしょう。ばねにかかる力が同じであれば、このように置きかえができます。そうすると、ばねの伸びは明らかに\(1\,\mathrm{cm}\)ですね。
皆さんはこのことを当たり前として認識できたでしょうか。できた人はばねのセンスがあるといっていいでしょう。それくらい誤解が生まれやすいポイントなのです。
応用問題に挑戦!
ここまでで、「ばねにかかる力のつり合い」についての解説は終わりです。最後に、今まで学んできた知識を使って、応用問題に挑戦してみましょう。応用問題とはいっても、これまでの内容を組み合わせただけなので、それぞれのばねについて落ち着いて考えればきっと解けると思います!
問題
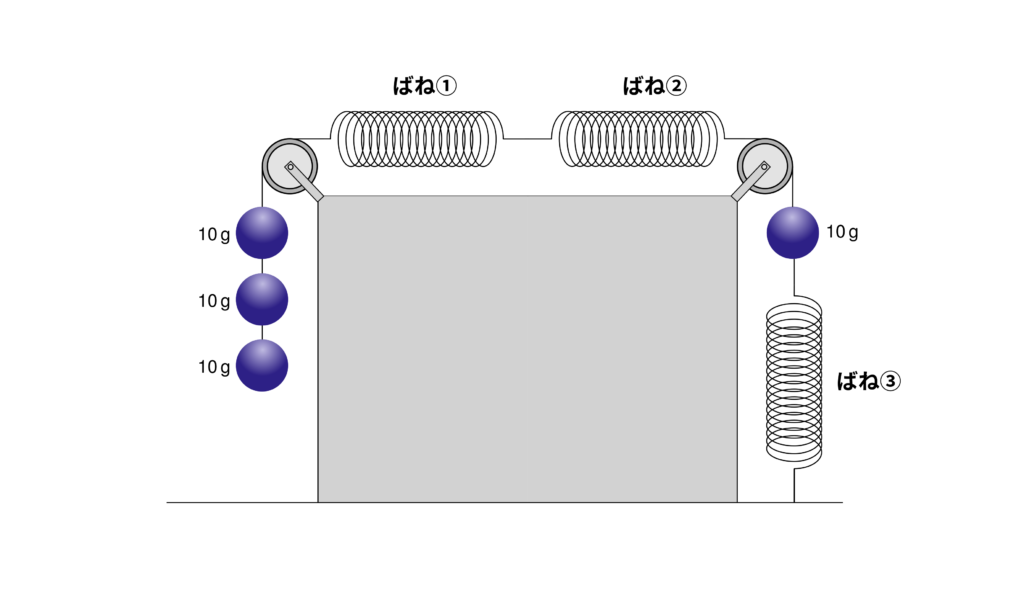
次の図のようにばね①~③とおもりが、滑車を通してつながっている。それぞれのばねの伸びを答えよ。ただし、ばねはおもり\(10\,\mathrm{g}\)あたり\(1\,\mathrm{cm}\)だけ伸びるとし、おもり一つの重さは\(10\,\mathrm{g}\)である。また、ばねの重さは考えないものとする。
解説
一見複雑に見える問題ですが、一つ一つのばねに分解して考えることで、正解に近づくことができます。まず、ばね①について考えてみましょう。前の問題と同じように、ばねに両側からどれだけの力がかかっているかを考えると、頭が整理されていくと思います。いま、ばねは静止しているので、ばねの両側にかかる力はつり合っています。そこで、ばね①の右側を壁に置きかえてしまいましょう。すると、ばね①は滑車を通して\(30\,\mathrm{g}\)のおもりをぶら下げた一つのばねと同じだと考えることができます。これは2番目の問題のおもりを\(30\,\mathrm{g}\)に変えた状況と同じですので、ばね①の伸びは
ばね①の伸び … \(30\,\mathrm{g} \div 10\,\mathrm{g} \times 1\,\mathrm{cm} = 3\,\mathrm{cm}\)
と求めることができます。
次にばね②ですが、ばね②はばね①と直列につながっているため、ばね②の両側にかかる力はばね①と同じく\(30\,\mathrm{g}\)になります。したがって、ばね②の伸びは
ばね②の伸び … \(30\,\mathrm{g} \div 10\,\mathrm{g} \times 1\,\mathrm{cm} = 3\,\mathrm{cm}\)
と求めることができます。
最後にばね③です。おそらくこれが一番厄介でしょう。力のかかり方を正しくイメージできるでしょうか。ばね③の力のつり合いを考える前に、おもり②にかかる力のつり合いを考えてみましょう。おもりも静止しているため、その両側にかかる力はつり合っています。ばね①と②で考えたように、おもり②もおもり①の力によって上側に引っ張られています。この力が\(30\,\mathrm{g}\)です。では、下側にかかる力はどうでしょう。先ほど、力がつり合っていると言った通り、おもりの下側には\(30\,\mathrm{g}\)の力が加わっています。しかし、この力の中にはおもり自身の重さ\(10\,\mathrm{g}\)が含まれています。よって、おもりの下側にあるばね③がおもりを引っ張る力は
ばね③がおもりを引っ張る力 … \(30\,\mathrm{g}-10\,\mathrm{g} = 20\,\mathrm{g}\)
となります。したがって、ばね③の両側にかかる力は\(20\,\mathrm{g}\)となります。この状況は、天井からぶら下がっているばね③に\(20\,\mathrm{g}\)のおもりをつけたものと同じです。したがって、ばね③の伸びは
ばね③の伸び … \(20\,\mathrm{g} \div 10\,\mathrm{g} \times 1\,\mathrm{cm} = 2\,\mathrm{cm}\)
と求めることができます。
いかがだったでしょうか。最初は複雑そうに見えた問題も、このように一つ一つ分解して考えれば、簡単な問題に置きかえ可能だということが実感できたと思います。
関連サイト↓
ばねの基本を理解する~自然長の意味とばねとばねにかかる力の比例関係~【中学受験理科】
まとめ
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。



















