本記事は場合の数・確率の攻略法【基礎編】【標準編】の続きの記事になります。もしこの分野に不安な箇所やわからない点があればそちらの記事を一読することをお勧めします。
今回はこの場合の数・確率という範囲からの出題に対応する応用力を養うために,過去の中学受験で出題された問題を引用し,一緒に解いて解説していくものです。これまで身につけてきた樹形図や余事象の考え方を使って,解き進めていきましょう。
Contents
問題を解いてみよう①
早速1問目に取りかかりましょう。頑張ればAから順番に道をなぞることでも求められそうですが,是非ここでは樹形図を作りながら解いてみてください。
下の図のような道があります。今,AからDまで移動するとき,通り方は何通りありますか。道は戻れますが一度しか通れないものとし,Dについた時点で終了するものとします。
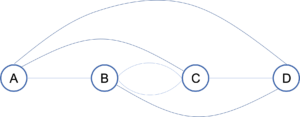
(湘南学園中学校(2015),一部改題)
解説①
それでは解説に移ります。この問題は何通りありますかという質問文から,場合の数が求められているものだとわかります。今回は1度しか通れない道の選び方なので,各地点から伸びている道の選択肢の数を考えていく必要があります.
ここでBとCを結ぶ道が2本あることが,問題を少し難しくしていますね。なぜ難しくなるのかというと,BとCを行き来することができるからです。そのためここでは上の道を①・下の道を②を呼ぶことにします。
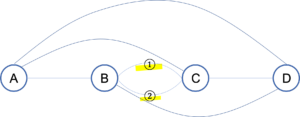
それでは出発点であるAから順番に樹形図を書いていきましょう。場合の数・確率の問題を解くときは必ず樹形図を作っていきましょう。特にこのように答えが単純なかけ算では求められないような問題では,慎重に計算するために図を作っていきましょう。
さて,地点AからはB・C・Dに道が伸びています。したがってまず2番目の列にB・C・Dという3つの要素が書き起こせますね。このときDについた時点で終了するため,A→Dという1通りが導けました。ここから終了したルートには○をつけていきます。この要領で各地点から伸びている道の数を考え,樹形図に表しましょう。
次にB・Cから繋がる道を考えます。BからはAへの道・Dへの道,そしてCへの道①と②の合計4本が伸びていますね。CからもAへの道とDへの道,加えてBへの道①と②の計4本が伸びていることがわかります。よってBとCからは下図のような4本の線を引きましょう。ただしBとAをつなぐ道・CとAをつなぐ道は,Aからの移動のときに通っているため使えません。そのため「ダメなルート」として×をつけました。それぞれの道が条件に沿うように通っているかを確認しながら進めましょう。
3列目もこれと同じように考えられますね。B・Cからは4本の道が伸びているため,4列目にも同様に4本の枝が書けます。そしてDにつながるルートには○を,これまで通った道を使っているルートには×を隣に書いていきます。
4列目で注意しなければいけないのは一度Aに帰ってくるルートの存在です。先ほどの3列目ではAに帰ってきたため×がつきましたが,今回はAに帰ってきても同じ道を使っていないためセーフな道順があります。またB→C→B/C→B→Cというルートでも,道①を使っているか道②を使っているかで成立することもあります。気をつけて解きましょう。
この後の5列目でもA・B・Cから伸びる道の数だけ枝を書き足していきます。画像のサイズが過度に大きくなってしまうためここでは省略しますが,5列目ではDに着く道しか残りません。そのためここですべての道順が終了し,樹形図が完成しました。以下ではこの図をもとに問題を解いていきます。
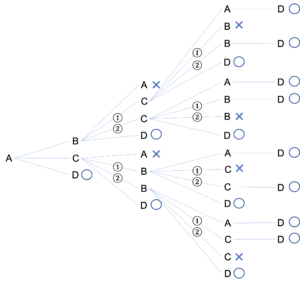
さて,改めて今回問われていたものを考えましょう。この問題ではAからDに移動する道順の数を答えればいいですね。このルートは,上の樹形図において○で表されていました。したがって○の数を数えていきましょう。○の数は全部で15個なので,答えは15通りとなります。このように樹形図を作らなければいけない問題では,問題文の指示と完成させた樹形図を照らし合わせていくことを忘れないようにしましょう。
問題①のまとめ
これで問題①の解説は終わりとなります。今回意識しておくべきポイントは次の3点でした。これらは他の樹形図が登場する問題でも活用できる技術なので,覚えておきましょう。
- 具体的な条件を考える前にまず樹形図を書こう!
- 樹形図を書いた後に問題文の指示と照らし合わせよう!
- 慣れてきたら樹形図を書きながら選択肢を絞っていこう!
A.15通り
問題を解いてみよう②
では次の問題に移ります。この問題は樹形図を使ってもいいですが,樹形図を使わなくても解くことができます。2通りの解説を用意しているので,解きやすい方法で取り組んでみてください。
右の図のようなA,B,C,D,Eの5つの部分を,赤,青,黄色の3色でぬります。となりどうしが同じ色にならないようにぬるとき,次の問いに答えなさい。ただし,2色だけでぬってもよいことにします。

(1)AとEが赤になるぬり方は何通りですか。
(2)2つの色だけを使うぬり方は何通りですか。
(明治大学付属中野八王子中学校(2019),一部改題)
解き方A かけ算を使う
解説(1)
それではここからは2問目の解説になります。まずご紹介するのは樹形図を使わずにかけ算で解く方法です。【基本編】の記事で紹介した通り,樹形図を使わなくても選択肢の数をかけることによって場合の数を求めることができました。例えば今回の問題において,何も条件が課されていない場合には5つの部分をそれぞれ3色でぬることができるため,すべての場合の数は3×3×3×3×3=243通りになるわけです。
ただし今回はとなりどうしが同じ色にならないように,という条件がつけられているので,この指示にしたがって(1)と(2)の問題を解くことにしましょう。
まず(1)から解いていきましょう。左から順番に入る色の数を考えていきます。いまAが赤でぬられるとき,Bにぬられるのは赤以外であるので,選択肢は青か黄色かの2通りとなります。同じようにCとDとにぬる色の選択肢を数えていきます。Cにぬることのできる色はBで使われていないものなので,青・黄色かのどちらか,または赤の2通りになります。
こうして次にDに塗ることのできる色を考えていくのですが,ここでひとつ厄介なところがあります。それはEにぬられる色が赤と指定されているところです。したがってDにはCとEの両方に使われていない色をぬる必要があり,考える要素が増えてきます。
このようなときはCにぬられる色が赤だった場合と,ぬられる色が青か黄色かのどちらかだった場合に分けて考えていきましょう。Cが赤だった場合Dは赤に挟まれることになるので,赤以外の2つの色,すなわち青と黄色の2色が使えます。一方Cが青か黄色だった場合,DにはCに塗られていない色が使われるため,青か黄色のうちの1色を塗ることができると考えられます。しかし赤色はDでは使えません。それはEが赤でぬられているからであり,となりどうしが同じ色になってしまうからです。このことからCが青か黄色だった場合,Cで使われていない青か黄色のどちらか1通りしか選択肢がないのです。
このことを要約すると次のような結論が出せます。Bでは2通りの色の選び方が考えられ,Cでも2通りが考えられる。このCにおける2つの選択肢のうち赤をぬるパターンではDのぬり方も2通りが考えられますが,他方青か黄色をぬるパターンではDのぬり方は1通りしか考えられません。以上をまとめると次のような計算式が立てられます。
2×(1×2)+2×(1×1)=6
このことから(1)の答えは6通りとなります。CをぬるパターンによってDの選択肢の数が変わってくるところに注目できたかどうかが,正しい答えを求められたかどうかにつながったかと思います。かけ算は簡単に計算を解くテクニックでもありますが,今回のようなパターンによる差を考えないと間違った答えを導いてしまうことになります。頭の中の考えや計算を常に問題文の条件と照らし合わせるということを心がけましょう。
A.(1)6通り
解説(2)
次に(2)を解いていきます。2色しか使わないぬり方の数が何通りか尋ねられていますね。ここで問題の条件を再度確認すると,となりどうしが同じ色にならないようにと指定されていました。
先ほどの(1)の問題で左から順番に色を決めていったことからもお気づきかもしれませんが,AとBまでで絶対に2つの色を使わなければいけないことがわかります。ここで先頭の2つの部分の色の組み合わせが決定すれば,残りのC・D・Eにぬる色は自動的に決定することは明らかです。
例えばAとBが赤・青の順番でぬられていたとしたら,それ以降の部分は赤・青の2色を使ってとなりどうしが被らないようにぬらないといけないわけですから,C・D・Eの順で赤・青・赤で確定しますよね。よってここからはAとBに何通りの色をぬることができるかを数えていけばいいわけです。
まずAにぬる色は赤・青・黄色の3通りから選ぶことができます。そしてBにぬる色は,A が赤であれば青か黄色・Aが青であれば青か黄色・Aが黄色であれば赤か青,すなわちAで使われなかった色以外の2通りから選べます。前述したように2通りしか使わない色のぬり方は,A・Bにぬる色の組み合わせの数を数えることで計算できるので,次の計算式が立てられます。
3×2=6
したがって答えは6通りとなります。このような問題だと樹形図を書くよりかけ算による計算の方が簡単に解くことができるということを実感しやすいのではないでしょうか。AとBにぬる色の組み合わせだけ考えればいいということに気づきにくかったかもしれませんが,さまざまなパターンの問題に触れることで次第に慣れていくことでしょう。いざというときは樹形図を使えば問題ないですが,テクニックの一つとして覚えておきたいところです。
A.(2)6通り
解き方B 樹系図を使う
次にご紹介するのは,樹形図にすべての色をぬる組み合わせを書き出し,その上で条件に合うものを絞っていく解き方です。さっそく順番に樹形図を書いていきましょう。
次の樹形図はAを赤色に設定し,となりに同じ色がこないという条件のもと書き上げた樹形図になります。まずはこの図を見て(1)の設問を解いていくことにします。
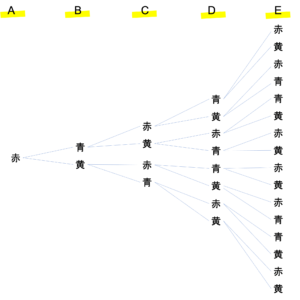
このようになりました。なぜ先頭であるAを赤に設定したかというと,最初の問題はAとEが赤色になるぬり方の数が聞かれているからです。この樹形図の中で,Eも赤色でぬられているものに印をつけていきます。
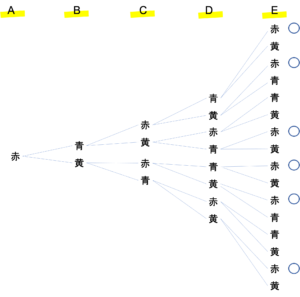
○がついたものが問題の指示に当てはまるものとなります。いま○は6つのぬり方に対してつけられているため,答えは6通りとなります。このように樹形図を作ることで問題をより正確に解くことができます。ただし図の作成に時間が取られては元も子もないので,図を書かないで解く方法にも慣れておくといいでしょう。
次に(2)の解説に移ります。先ほどAを赤としたときの色の組み合わせを図に表しましたが,これと同じようにして,Aが青のとき・Aが黄色のときの樹形図も作っていきます。このとき,2色だけでぬられているものにマークをつけておきましょう。
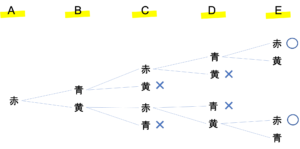
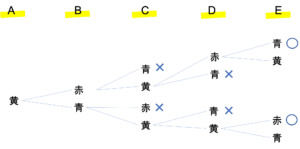
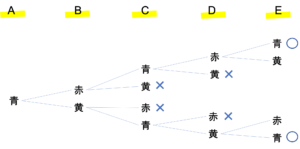
この樹形図では,3種類の色がぬられているものに対してその時点で×をつけています。○は2つの色しか使っていないぬり方になります。○の数は全部で6個なので,答えは6通りとなります。
A.(1)6通り,(2)6通り
樹形図を作りながら条件に合わないものを消していくと,効率的に選択肢を絞り込めます。この条件に満たないものを取り除くという手法は余事象の考え方の応用ですね。正確に答えを導くことが最も大事ですが,同時に早く効率的に解くことを心掛けておくことも,中学受験では極めて重要です。たくさん問題を解いて,計算スピードを上げていきましょう。
問題②のまとめ
これで問題②の解説は終了です。かけ算で問題を解くか樹形図で問題を解くかで重要となる点は異なりますが,この問題におけるポイントは大きく次の2点になります。
- 指定された条件を確認しつつ計算することで,簡単に問題を解く糸口をみつけよう!
- 余事象の考えを活かして樹形図を作りながら条件に合わないものを消していこう!
まとめ
今回は場合の数・確率という範囲に焦点をあて,入試で出題された応用レベルの問題をご紹介し,解説していくというものでした。本記事では2問しか取り上げられませんでしたが,続きの記事である【応用編2】の方にまたいくつか問題を引用しておりますので,物足りない・もう少し演習を積みたいという方はそちらを参照していただけたらと思います。本記事が学習の手助けとなれば幸いです。
(ライター:大舘)
おすすめ記事
参考