今回の記事では資料の読解について,受験問題をいくつかご紹介しながら,本番でも活用可能な解答テクニックを交えながらご紹介していきます。この資料の読解という分野では表やグラフが登場しますが,受験生にとってこれらの図表はなかなか目に入る機会が少ないことから,苦戦してしまう人が多いです。本記事ではまだまだ算数が苦手な人はもちろん,すでに入試本番を意識している受験生にも役に立つような知識を解説していますので,よければ一読していただけますと幸いです。
資料・データとは…?
そもそも中学受験で登場する資料やデータとはどんなものを指すのでしょうか。以前の記事では代表地とグラフについて細かくご紹介しましたが,受験問題を解説していくにあたって軽く復習しておきましょう。
データ・資料とは,何らかの調査などの結果得られた情報を表す数字や図表のことを指します。このうち代表値というものは情報の特性を一口で表すための判断材料となる数字のことで,グラフや表というものは情報の全体像をパッと見で分かるように表した図形を指します。
このうち具体的に覚えておきたいものとして,まず代表地の中だと平均値がありますね。平均とは個々のデータを全て足し合わせた数を,数値の個数で割った値です。この値は特に中学受験ではよく出てくるので,中央値・最頻値といった他の要素よりも優先して覚えておきたいところです。
グラフや表の中だと,棒グラフや円グラフといったものはもちろん重要ですが,受験生が悩みやすいかつ登場しやすいグラフとしては度数分布表とヒストグラムが挙げられます。これらはともにデータの散らばり具合を見るのに使われるものです。棒グラフと形が似ていますが,この度数分布表・ヒストグラムは区間ごとに当てはまる数を数え上げているという特徴があります。他の受験生が苦戦しやすいところなので,ぜひ覚えておきましょう。
ここでご紹介したデータ・資料の重要用語は一部に過ぎないので,よろしければ先ほどもご紹介した過去の記事を参考にしながら頭に入れていただけますと幸いです。また同じ形のグラフや表だとしても問題によって見るところが変わってくるので,ある程度用語を覚えられたら応用力を身につけることを意識していきましょう。
問題① 表から合計や平均を割り出そう!
まずはシンプルな表の問題にチャレンジしていきましょう。この問題では計算式をどうやって作るか,がポイントになってきます。どこから求めれば答えが割り出せそうか,を意識しながら取り組んでみてください。
A,B,C,D,E5人の志願者に実技試験と筆記試験をしました。それぞれの満点は10点,20点で,A,B,C,D4人の得点は下の表の通りです。合計点の5人の平均点はちょうど20点でした。
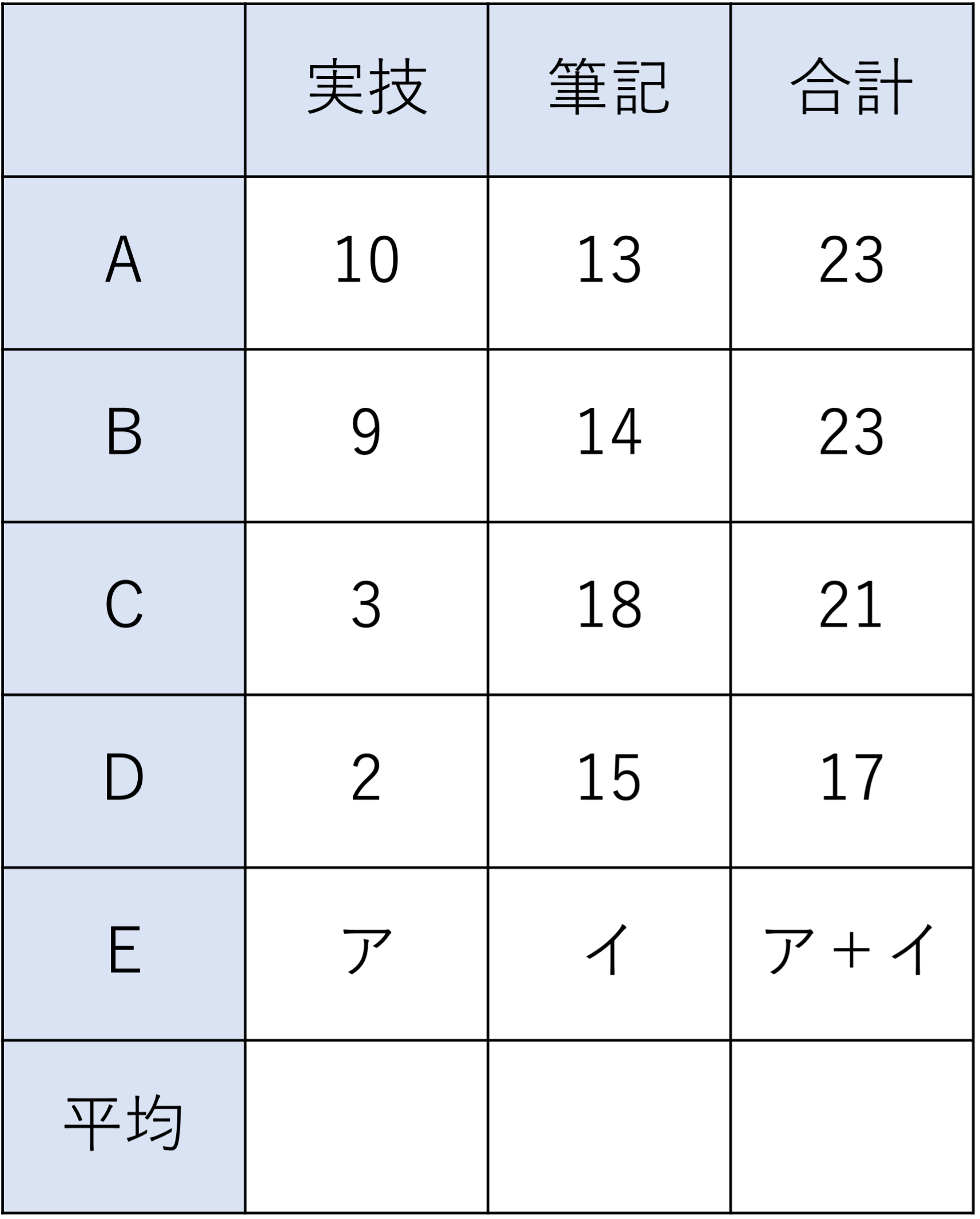
(1)Eの合計点(ア+イ)は何点ですか。
(2)A,B,C,D4人の実技の平均点,筆記の平均点はそれぞれ何点ですか。
(久留米大学附設中学校(2014),一部改題)
解説①
それではここからは解説に移ります。
(1)まずはEの合計点を考えなければいけないのですが,ここで不慣れな人だとアとイをそれぞれ求めてから合計を計算すればいいのかと考えてしまいがちです。しかし今回の問題では5人の合計点の平均が示されているので,直接Eの合計点を求めた方が早そうですね。このように(ア+イ)といった式の形に騙されず,登場している情報から近道を探すことを重視していくといいでしょう。
さて,それではEの合計点を求めるために5人全員の平均について考えてみましょう。平均点とはAからEの5人の合計点を足して5で割った値のことを指すので,上の表について次の式が成立しますね。
(Aの合計+Bの合計+ Cの合計+ Dの合計+ Eの合計)÷5=平均点
(23+23+21+17+ア+イ)÷5=20
この式について(ア+イ)の部分を計算するために,数字をそれぞれ右に移して中身を整理すると,次のように式は変形でき,その結果Eの合計点は次のようになります。以下のように()を外して数字を移してまとめるというテクニックは色々な計算で使えるので,ぜひ身につけておきましょう。
(23+23+21+17+ア+イ)÷5=20
ア+イ=20×5-(23+23+21+17)
ア+イ=16
A.16点
(2)続いてはAからDの4人の実技の平均点と筆記の平均点を計算していきましょう。ここでありがちなケアレスミスとして,Eの値を合わせた5人の平均点を考えてしまうというものが挙げられます。中学受験のほとんどの問題が(1)の答えを(2)で使い,(2)の答えを(3)で使い,……という構造をしているので騙されやすいですが,このように前問の答えとは関係ない問題もありますので,問題文の読み取りには注意しましょう。
さて4人の平均点ですが,(1)で見たように平均点とは全員の値を足して人数で割った値を指すので,それぞれの値は次のように計算できます。
(Aの実技+Bの実技+ Cの実技+ Dの実技)÷4=実技の平均
(10+9+3+2)÷4=6
(Aの筆記+Bの筆記+ Cの筆記+ Dの筆記)÷4=筆記の平均
(13+14+18+15)÷4=15
したがって答えは次のようになります。この問題をはじめとして,平均点は様々な学校で登場しやすい代表値の一つだといえます。それゆえ計算方法をしっかり覚えた上で,計算スピードをできるだけ早くすることを心がけていきましょう。
A.6点,15点
問題②
2問目は帯グラフが登場する問題です。やや高度な内容の読み取りが求められる問題ではありますが,詰まったらどこが何人なのかを考えつつ進めていくといいでしょう。
下の帯グラフは,あるクラスでおこなった10点満点のテストの結果を表したものです。次の問いに答えなさい。
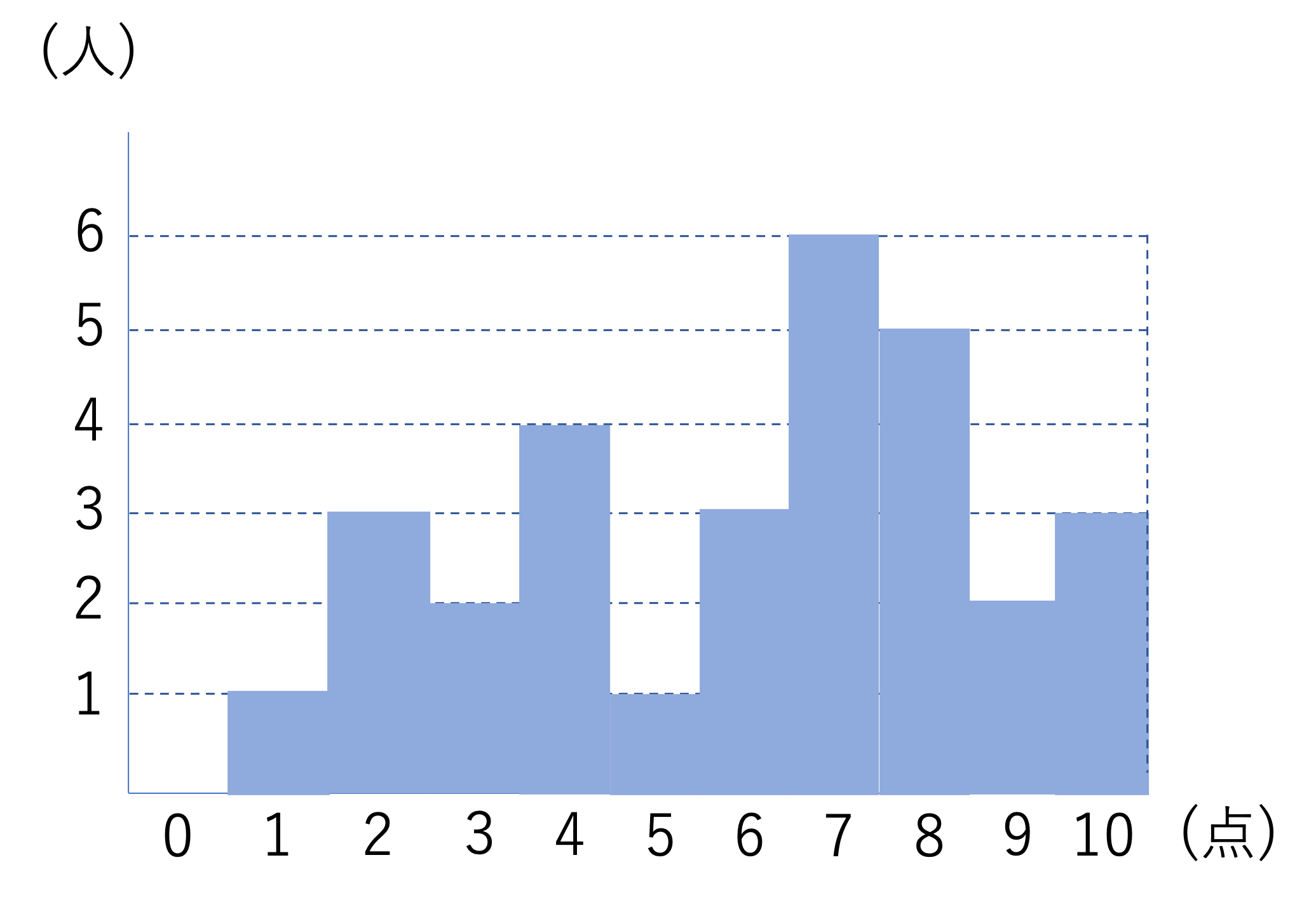
(1)5点の生徒は,上位から何番目ですか。
(2)クラスの平均点は何点ですか。小数第二位を四捨五入して,小数第一位まで答えなさい。
(跡見学園中学校(2019),一部改題)
解説②
それでは2問目の答えについても振り返っていきましょう。
(1)初めに考えるのは5点の生徒の順位ですね。いまこの問題では5点の生徒は1人しかいないのですが,その人が上から何番目かを数えていきます。上から何番目かと述べましたが,ある点数を取っている人の順位は,それより高い点を取っている人の数に1を加えた値になります。例えば6点以上の人が3人いれば,5点の人は3+1=4位となるわけです。この要領で上の帯グラフを見ていくと,6点が3人・7点が6人・8点が5人・9点が2人・10点が3人いるので,5点の人の順位は次のようになります。
(3+6+5+2+3)+1=20
A.20番目
(2)それでは続いて平均点を計算していきましょう。この問題は先ほどの問題の(2)に近いですが,大きな違いは答えが小数になるというところです。平均点の計算では割り算が登場しますが,それゆえ値が割り切れないことも多々あります。値が整数にならなくても,焦らず計算を続けていきましょう。
さてそれぞれの点数と人数ですが,ここで平均点を計算する上で重要なテクニックとしてのかけ算のやり方を覚えていきましょう。これまでの計算はすべての数を足し合わせていましたが,それだと時間がかかってしまいますね。それゆえ素早く計算するための方法として,同じ点数を取っている人は点数×人数としてまとめて計算してしまいましょう。この手法を使うため,先ほどの6点以上の人を数えたのと同様に,それぞれの点数が何人かを数えていくと,次のようにまとめられます。
0点:0人,1点:1人,2点:3人,3点:2人,4点:4人,5点:1人,6点:3人,7点:6人,8点:5人,9点:2人,10点:3人
したがって点数×人数という計算式をもとにこれらの合計を数え,人数で割ることで答えを出していきましょう。このとき今回は0点から10店までデータの幅が広いので,合計と人数とをバラバラにカウントし,最後に割り算をすることでミスを減らしていきましょう。
合計:1+(2×3)+(3×2)+(4×4)+5+(6×3)+(7×6)+(8×5)+(9×2)+(10×3)=182点
人数:1+3+2+4+1+3+6+5+2+3=30人
平均点:182÷30=6.066……点
そして今回の問題では小数第二位を四捨五入しろという指示が与えられているので,答えは6.1点となります。この四捨五入や繰り上げ・繰り下げといった部分の指示は問題によって様々なので,きちんと文章を読んでおく癖をつけておきましょう。
A.6.1点
問題③
ここからは最後の問題になります。この問題ではグラフに近いような形をした表が登場しています。なかなか見慣れない形なので戸惑う人も多いでしょうが,まず設問の答えを考える前に,この表はどういう構造をしているのかをじっくり考えてみるといいでしょう。
あるクラスで国語と算数のそれぞれ5点満点のテストを行いました。下の表は,その得点と人数をまとめたものです。例えば国語が3点で,算数が4点の人は3人います。空欄は0人です。このとき,次の問いに答えなさい。ただし,割りきれないときには,小数第2位を四捨五入すること。
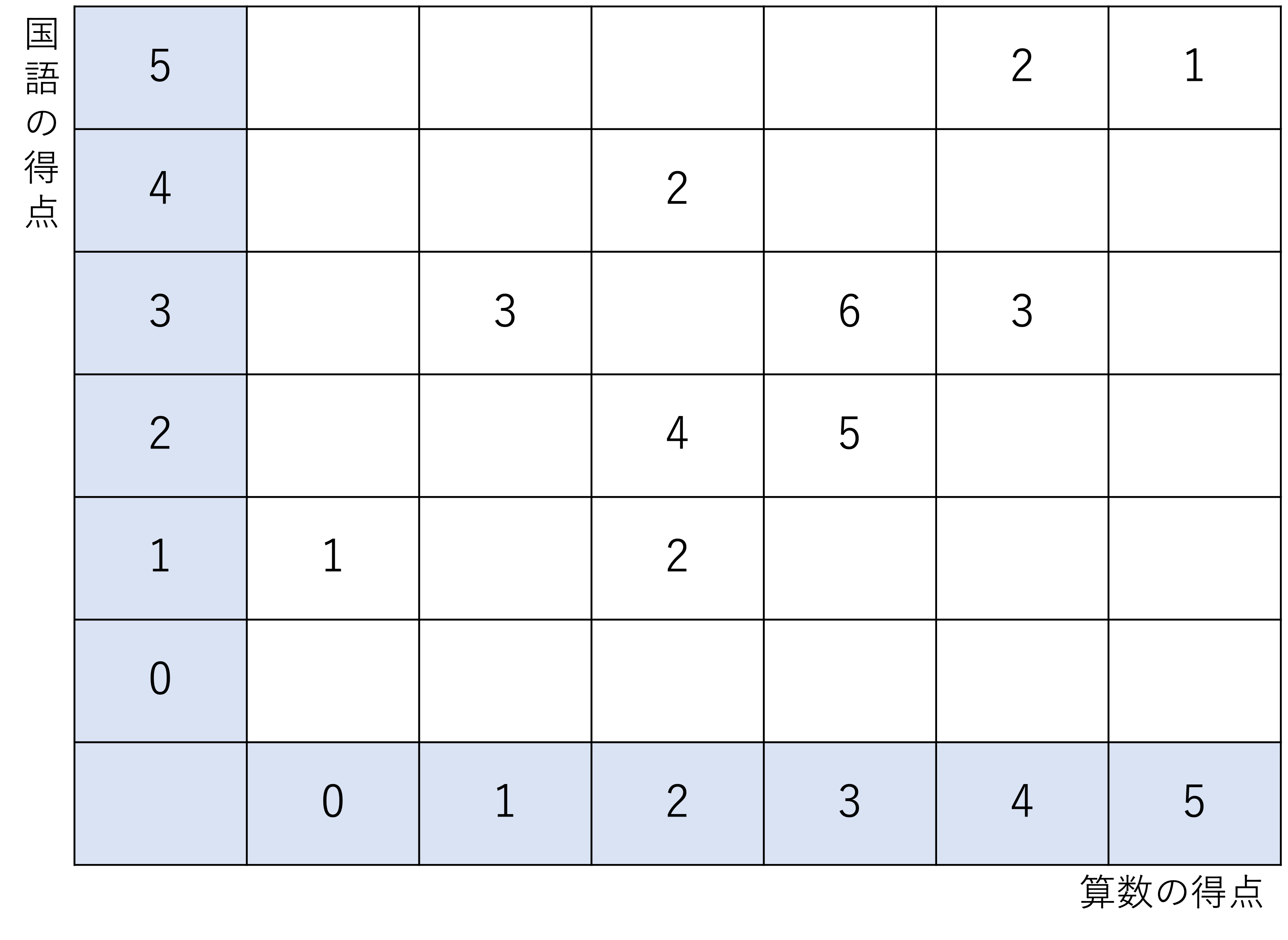
(1)国語の平均点は何点ですか。
(2)国語の得点の方が算数の得点よりも高い人は,クラス全体の何%ですか。
(跡見学園中学校(2018),一部改題)
解説③
それでは3問目の解説をして本記事を締めくくっていきます。はじめにこの表の見方を確認していきましょう。この表はいわばグラフのような形をしていて,縦軸と横軸にそれぞれの点数があり,国語と算数でとっている点数にしたがってマス目に当てはまる人数を書き込んでいく,という仕組みで作られています。やや見慣れない形ではありますが,基本の形は表と同じですので,あまり難しく考えすぎず進めていきましょう。
(1)まずは国語の平均点ですね。先ほどの2問目の(2)で行った計算と同じ要領で数を数え上げて計算を進めていきましょう。このときの数え方ですが,横軸に沿って眺めていき,横軸の値を足していくことで各点数の人数は数えられます。例えば国語が1点の人は,国語が1点・算数が0点の1人と,国語が1点・算数が2点の2人が該当するので,1+2=3人存在することになりますね。この要領で0点から順番に数えていくと,
0点:0人,1点:3人,2点:9人,3点:12人,4点:3人,5点:3人
であることがわかるので,これに沿って合計と人数を計算し平均を求めると,答えは次のようになります。
合計:(1×3)+(2×9)+(3×12)+(4×3)+(5×3) =84点
人数:3+9+12+3+3=30人
平均点:84÷30=2.8点
A.2.8点
(2)続いて国語の点数が算数の点数より高い生徒を数えていきましょう。ここで,今回求めるべきものが割合であることに注意しておきましょう。データや資料を読解する問題では,このように割合や比を計算する問題なども登場します。そのためいろいろな分野への理解が不可欠になるので,表やグラフの読み方以外の知識も身につけておきたいところです。
さて,この表において国語が算数より高い生徒の数を数えていくわけですが,ここでは国語が1点・算数が0点の1人,国語が3点・算数が1点の3人,国語が4点・算数が2点の3人,国語が5点・算数が4点の2人が該当するわけですね。これらの人数を合計すると1+3+3+2=9となるので,該当する人数は9人となります。いま(1)で見たようにクラスの人数の合計は30人だったので,答えは次のようになります。
9÷30×100=30%
A.30%
終わりに
今回の記事では資料の読解という単元に着目して,攻略法をご紹介していきました。この範囲は空間図形や文章題に比べると大々的に取り扱われることが少ないですが,それでも対策が欠かせない大切な範囲だと言えます。よろしければ下のおすすめ記事や参考書籍を使いながら,更なる学習を進めていただけますと幸いです。本記事が今後の学習のお役に立てば幸いです。