今回の記事では前回の内容に引き続き,虫食い算の解き方についてご紹介していきます。虫食い算とは小学校低学年で習う計算をベースとした文章題であるものの,数学的なセンスが問われるので苦戦しやすい範囲だともいえます。それゆえに対策が必須な単元ですので,本記事を使いながらぜひ力をつけていただけますと幸いです。
Contents
虫食い算とは…?
今回の記事では3つの入試問題を使いながら虫食い算を解く際のポイントを応用的な観点から説明していきます。しかしその前に,前回の基礎編でお教えした虫食い算とはどういった問題なのか・虫食い算はどうやって解くのかということを振り返っていきましょう。
虫食い算とは,端的に言ってしまうと筆算の穴埋めを行うことが求められる算数です。通常の筆算はいくつかの数字を縦に並べて位ごとに計算していきますが,その計算過程の一部が□で分からなくなっているのがこの虫食い算であり,その中身を考えて推測するということが求められます。

虫食い算を解く際のポイントはそれぞれの位ごとに式を組み立てていくことです。これは+・−・×・÷のどの計算においても当てはまります。例えば32 +4□= 76という計算があったとして,2つの式を立てることで□の中身を推測していくというわけです。今回の問題であれば一の位に関して2+□=6という計算式が作れますが,この式で逆算を応用すると,□の中身は4だと分かるということです。もちろんこの程度の計算であれば頭の中で答えを導けるかもしれませんが,けた数が増えたり繰り上がり・繰り下がりが起こったりする問題もありますので,基本的な解答方法は身につけておくといいでしょう。
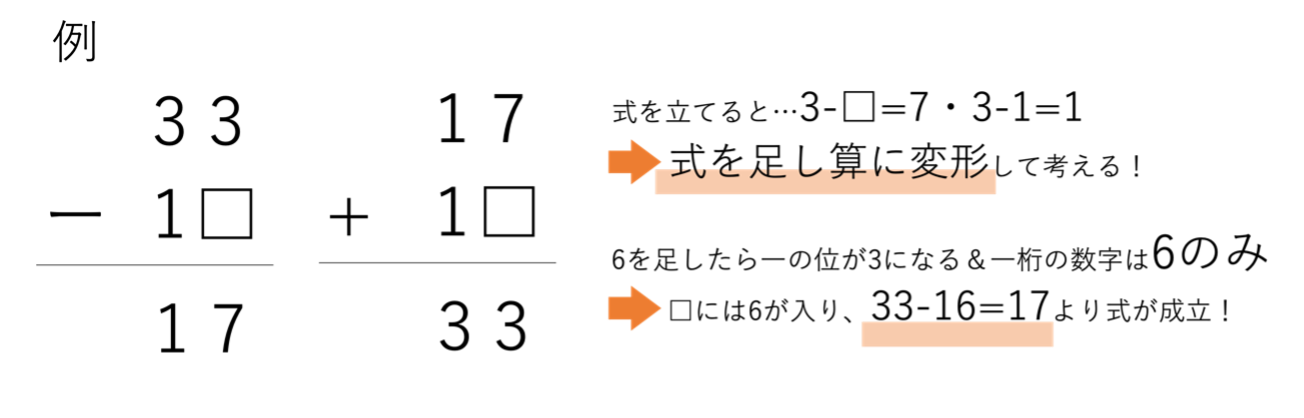
なお繰り上がり・繰り下がりについて触れましたが,筆算の繰り上がり・繰り下がりを利用した虫食い算も出題されます。そのような問題に出会ったら位ごとの式を立てていくだけでなく,繰り上がりの場合は計算結果の末尾に注目する,繰り下がりの場合は足し算に変形して計算すると効率よく答えを導けます。もちろんいろいろな解き方がありますが1つの方法として参考にしてみてください。
問題① けたの多い虫食い算に慣れていこう!
まず1問目はシンプルな虫食い算になります。シンプルとは言いながらも,前回ご紹介した2けたの虫食い算よりはだいぶ解きづらいと思われるかもしれません。しかし基本的な原則を使っていけば無事解くことができますので,ぜひ自分の力でチャレンジしてみてください。
次のかけ算について,ア〜キにそれぞれ1から9の数字が当てはまります。ア,イ,ウにあてはまる数字をそれぞれ答えなさい。

(開智中学校(2009),一部改題)
解説①
ここからは解説に移ります。この問題ですが,空欄のうちア・イ・ウの3つの値を求めよと言われています。そのため解き始める際上の方から着目してしまいますが,ここで大事なのが答えを求める部分にとらわれずに問題を捉えるということです。この原則はどんな文章題にも当てはまりますが,答えに気を取られるあまり悩みすぎてしまうことが受験生には多々あります。今回であれば7つも空欄があるので,そのうち最も埋めやすいところから考えていきましょう。
今回の筆算は3アイという数とウエという数のかけ算の問題です。通常かけ算の筆算はかけられる数をかける数のそれぞれの位とかけ合わせ,その結果求められたいくつかの数を足し算していきますが,今回の問題ではかけ算の結果7オ4という数と2カキ20という数が算出され,その2つの数を足すことにより24614という答えが求められるわけです。ここでこのうちの後者の足し算に着目し,虫食い算を解く基本であるところの位ごとの式を立てていきましょう。その結果次のような5つの式が立てられます。
4+0=4,オ+2=1,7+キ=6,0+カ=4,0+2=2
これらの式から,直接的な答えではないものの,問題の穴を次々に埋めていくことができます。まずオ+2=1という式に着目してみましょう。この式は答えが足す数の2よりも小さいので繰り上がりが発生していることがわかります。したがってオは2を足すと末尾が1になる1けたの数だと推測できるのですが,これを満たすのは9しかありません。したがってオ:9だと判断できます。このようにして繰り上がりした際は末尾に注目しつつ,徐々に虫食いを埋めていきましょう。次に7+キ=6という式ですが,こちらでも答えの6が7より小さいので繰り上がりが発生しています。しかし十の位と同様に計算してしまうと正しい答えが出せません。それは十の位の足し算によって1の繰り上がりが発生しているからです。前の位で出た余剰,または引かれた不足をきちんと考えないと答えが1ずつずれてしまうので気をつけましょう。今回の式は繰り上がりの結果次のように更新されるので,キの値は8になります。
(7+キ)+1=8+キ=○6
キ:8
さて続いてカに移りましょう。この式も一見カ:4だと考えてしまいがちですが,百のくらいの計算結果で1の繰り上がりがまた発生していることから,正しい式は(0+カ)+1=4となり,カ:3となります。以上で求めたカ・キ・クの計算結果を一度筆算にまとめてみると,次のような結果が導かれます。

このように,分かりやすい足し算の部分に注目することで,2つの数をかけたときにどういう値が算出されるのかを求めることができました。それではここからは,以上のように求まった数を基準に,どのような数がアからエまでに入れば計算が成立するかを考えていきましょう。これも計算の順序に沿って値を考えていきましょう。かけ算の筆算はかけられる数とかける数の一の位をかけるところから計算が始まるので,まずは3アイ×エの部分に注目していきます。このかけ算の答えが794になっているわけですが,ここで3アイの範囲を考えてみましょう。3アイはどれだけ小さくでも300にしかならないわけですが,この数に仮に3以上をかけてしまうと導かれる値が900以上となり,794を超えてしまいます。他方1をかけてしまうと今度は大幅に数が足りないわけです。そのため794の中に含まれる3アイの最大の個数を考えることで,エの値が2だとわかります。そしていま一の位のかけ算に注目するとイ×エ=4という式が出来上がるわけですが,ここでエの値が2だとわかったため,2をかけて末尾が4になる数字を考えると,イの中身が2か7だと求められます。
さてここで2択の答えが考えられるため,困惑してしまった方もいるのではないでしょうか。このように条件を設定しても答えが定まらない場合は,それぞれの場合について計算を進めていったときにちゃんと式が成立する方が正しい答えだ,という展開で計算を進めていきます。例えば今回の問題であれば3ア2と3ア7の両方のパターンで2をかけてみて,794が作れるものを選べばいいというわけです。さて3ア2の場合,一の位は2をかけて4になりますが,十の位はどうやっても9になりません。それは偶数に何をかけても答えは偶数になってしまうからです。他方3ア7の場合,一の位をかけ算したときに十の位に1が繰り上がりますので,ア×2の値が偶数にしかならないとしても9が作れるというわけです。このことと,百の位の計算である3×2をしても7には1足りないということから,アに当てはまるのは2をかけて1を足したときに末尾が9になる上で繰り上がりが発生する数,つまりは9であることが分かります。
そして最後にウの答えですが,ここで十の位の計算に着目すると,397×ウ=2382という式が出来上がります。この式を逆算によって変形し2382÷397=ウという式を作ると6という値が求まり,結果として問題の答えは次のようになります。
A.ア:9,イ:7,ウ:6
このように穴が多い問題は答えとなる部分に捉われずに問題全体を見渡し,その上で原則を活用しながら,それぞれの穴に入る数字の条件を絞っていったり仮定したりしながら計算を進めることでスムーズに答えが求まります。慣れないうちは難しいかもしれませんが,たくさん問題を解いて慣れていきましょう。
問題② 穴の多い虫食い算にチャレンジしてみよう!
次は穴の多い虫食い算になります。最後の答えがどの位も明かされていないため,どこに注目すればいいのか分かりづらいでしょう。ヒントとしては○・△・□の条件を頭に入れながら考えていただきますと解きやすくなりますので,ぜひその点を意識してみてください。
小さいものから順に並べた6つの異なる整数1,○,△,5,□,8があります。この6つの数を並べてできる次の2つの6けたの整数1○△5□8と8□5△○1の和が7けたの整数になりました。この7けたの整数を答えなさい。
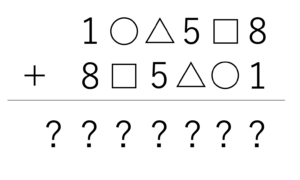
(東大寺学園中学校(2015),一部改題)
解説②
さてここからは2問目の解説を進めていきましょう。今回の問題は先ほどの問題よりも空欄の数が多く,ヒントの少なさから戸惑った人もいるかもしれません。しかし問題文をじっくり読んでいくといくつかのヒントが見つけられます。1問目の解説の中でもお話ししましたが,重要なのは答えをそのまま導こうとするのではなく,分かるところから着実に穴を埋めていくということです。今回の問題であれば○と△と□の範囲が決められていること・出来上がる整数が7けたであることをヒントとして,いくつか考えられることがありそうなのでまずはそこを検討していきましょう。
はじめに○ △ □の範囲を考えていきます。今回の問題では6つの異なる整数が小さい順に登場していました。この並びを見ると○は2か3か4のいずれかで,△も2か3か4のいずれか,□は6か7のどちらかあることができますね。かつそれぞれの整数はどれも被らないこと,また○より△・△より□のほうが大きいことから,穴に当てはまる整数の可能性としては○が2か3・△が3か4・□が6か7であることが分かります。
続いて7けたの整数の中身を見ていきましょう。まずは原則通り位ごとの式を立てると,答えの一の位の数は8+1=9であることが分かります。残りの数については○・△・□の中身が特定できないと計算できなさそうですが,ここで最も大きい十万の位に注目してみましょう。いまこの位では1+8という式が立てられますが,このときの答えは9とならずにけたが1つ増えていますよね。それゆえ一万の位で発生した繰り上がりにより十万の位で1増えて,答えの位が一つ大きくなったのではないかという推測をすることができます。それゆえ初めの2つの?には10が入ると導くことができ,かつ一万の位では繰り上がりが発生していることが分かりました。
ここで繰り上がりの発生する条件に注目してみましょう。一万の位で繰り上がりが発生するとき,当然のことながら○+□という足し算の結果が10以上にならなければいけませんよね。ここで○が2か3・□が6か7という前提より,◯+□の値はどんなに大きくても10にしかならないことが分かりますので,○の中身は3・□の中身は7であると導けます。このように範囲という条件と和という条件の2つから穴の中身を埋めていくことができますので,やはり様々な条件から中身を絞っていくことが重要だと理解していただけますと幸いです。さて○の中身が3であるとき,○の中身である3より大きく5より小さい整数の□の中身は4になりますので,筆算は次のように更新することができます。
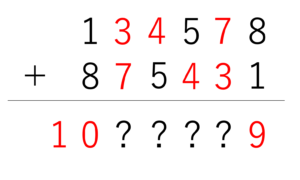
以上の過程により元々の2つの6けたの整数の中身がわかったので,あとはその足し算を完成させることで答えを導きましょう。134578+875431=1010009であり,この値は初めの2けたが10・末尾が9であるという条件にも合致するため,答えは下のようになります。
A.1010009
問題③
それでは最後にかけ算の虫食い算の計算を解いて本記事を締めくくっていきます。この問題は2問目と似たような構造になっていますが,ヒントや条件を探し出すのが難しいかもしれません。一の位と百の位に注目してみると解きやすいかと思いますので,参考にしてみてください。
ある3けたの整数があります。この3けたの整数ABCの一の位の数と百の位の数を入れ替えて,もう1つの3けたの整数CBAをつくります。2つの整数をかけたら,下の計算のように答えが115245になりました。十の位の数Bはいくつですか。
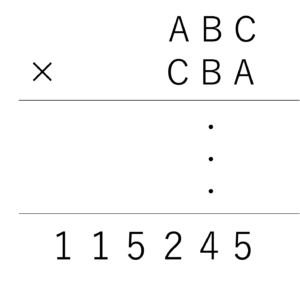
(公文国際学園中等部(2011),一部改題)
解説③
それではここからは最後の問題の解説を進めていきます。といってもどこから手をつけていけばいいのかが掴みづらいかと思いますので,まずは基礎編でご紹介した攻略法の通りに位ごとの式を作ることで条件を考えていきましょう。はじめに一の位です。かけ算における一の位は,かける数とかけられる数の一の位同士のかけ算の結果のみで決まります。そのためこのようなかけ算の虫食い算では末尾に注目することを大切にしていきましょう。さて今回の答えの末尾である5ですが,1けたの整数でかけたら末尾が5になる組み合わせは下の5通りが考えられます。
1・5,3・5,5・5,7・5,9・5
このうちのどれが正しいAとCの値なのかをまずは考えていきましょう。はじめにAとCが同じ値になっている5・5はハズレになりますね。というのもAとCの値が同じだったらABCとCBAが同じ値になってしまうからです。問題文にももう1つの3けたの整数という記述がありますので,文章の一字一句を見落とさないようにヒントを探していきましょう。
さて残りの4つのうちのどれかがAとCの値になるわけですが,ここで同じくAとCが関係する百の位を見ていきましょう。ここに注目すると,AとCをかけ算した結果が11を超えてはならないことが分かります。例えばAとCが9・5という組み合わせだったとして,できる3けたの数は5B9と9B5ですよね。この2つをかけ算すると,500×900の時点で450000となってしまい,答えである115245 を超えてしまうわけです。そのためかけ算したときの結果が答えをオーバーしないかという要素に注目すれば組み合わせを絞っていける,というわけです。ではオーバーしない組み合わせはどれかというと,今回の問題ですと1・5の組み合わせしか残りませんので,AとCには1と5が当てはまります。このときAが1・Cが5なのか,それともAが5・Cが1なのか気になる方もいらっしゃるかと思われますが,今回の問題ではAとCが逆であろうと出来上がる2つの3けたの整数は同じで計算の答えも同じになり,かつ答えはBの値しか問われていないので,適当に決めてしまって問題ありません。時間をかけなくてもいいところはかけずにショートカットを意識していきましょう。ここまでの結果をまとめると下の図のようになります。

あとは計算を進めながらBの値を求めたら解答が完了しますね。ここでまた位ごとの式に戻りましょう。このように視点を切り替えていくことは難しいテクニックではありますが,難問を解く上では必須の考え方になります。日頃から意識しておくといいでしょう。さて一の位の式は上で確認したので十の位の式を見ていきましょう。一の位には5×1の結果が現れますが,筆算の進め方を基準に同じようにして十の位についても考えると,この位には1B5×1のうちのB×1というかけ算と,1B5×Bのうちの5×Bというかけ算の結果が反映されますね。そのためそれらを足した1×B+5×B,つまりは6×Bの末尾が4になっていればいいわけです。ここで6をかけると末尾が4になる整数にはどんなものがあるかを考えると,4(かけると24)と9(かけると54)の二択が浮かぶと思われます。しかしここまでだとその二択を絞りきれないので,また同じようにそれぞれのパターンでかけ算を実際に行なって答えを絞っていきましょう。
まずB:4のときですが,このときかけ算は145×541となり,その答えは78445となります。他方B:9のとき,かけ算は195×591となり,その答えは115245となります。このことから答えとなるBの中身は9となるわけです。
A.B:9
なお今回はBに考えうる値を代入してかけ算を行いましたが,実際の入試で3けたのかけ算を2回も行なっていると大幅な時間のロスになります。そこで役に立つのががい算の考え方です。例えば145×541はがい算によりどんなに大きくても150×600=90000程度にしかならないことが分かり,他方195×591は200×600=120000程度になるためより答えの値に近いためB:9だと判断できます。このように基本的な計算の技術はいかなる場面でも応用可能ですので,この機会に頭に入れ直してみてはいかがでしょうか。
練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
≪入手方法≫
※画像はあくまでイメージです。本来送られるものとは違いますのでご了承いただけますよう、よろしくお願い致します。
①以下のリンクから公式LINEを友だち追加
②送信される画像をタップ!
パスワードで保護されている記事へと移動します。

③パスワードを入力(パスワードはLINEの友だち追加時に送信いたします。)
※パスワードを入力しても見ることができない場合、もう一度入力していただくか、キャッシュ機能の設定を変更するなどしていただきますよう、お願いいたします。

④スクロールしてPDFをダウンロード!

<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>
QR.png)
まとめ
虫食い算はいかがだったでしょうか?最後の方では応用問題もいくつか出しましたが、まずは確実に基本問題を解けるようにしましょう。四則演算全ての虫食い算をきっちり練習して定着を図っていってください!