算数を得意にするには学年の終わりが関門！苦手単元克服法

中学受験で一番難関だと感じるのが算数ですよね。中学受験の算数は受験算数と呼ばれ、小学校で学習する範囲を超え、また見た目もさまざまで、攻略するには一筋縄ではいきません。

基本的には４年生からはじまる受験カリキュラムの中で、各単元を学んでいきますが、受験算数の特徴として、４年生の内容を理解していることを前提に５年生でさらに深く細かく学習し、６年生になるとそれらを前提として総合問題、融合問題に取り組んでいく、というステップを踏みます。

塾などでは「らせん状に何回も同じ単元を学習するので心配はいりません」と説明を受けることも多いのですが、それは前の学年で学んだ内容が身についていることが前提なので注意が必要です。いくらもう一度出てくるからと言って、そこで改めて一から教えてもらえるわけではないことを知っておきましょう。

そのため、各学年で学習した内容をその学年のうちにしっかり理解しておくことが、次の学年での学習をスムーズに進めるためのカギになります。それができていないと、単元で何を学ぶのかが理解できず、問題を解こうとしてもどの公式、どの解法を使って解けばよいのかがわからなくなり、いわゆる「つまずき」の下になってしまいます。

中学受験の算数は単元が非常に多岐にわたります。計算問題にはじまり図形、特殊算の文章題、一行問題などさまざまな形で算数の理解を問うので、一度つまずいてしまうとリカバーするのに時間がかかってしまい、理解が穴だらけになってしまうと総合問題を解くときに途中まではできても解ききれない、ということになってしまいかねません。だからこそ、前の学年の学習内容をしっかり理解して次の学年に進むことが何より大切なのです。

中学受験を目指す受験生にとって特に関門となる単元は、４年生の後半や５年生の後半に集まっています。そこで学習する内容は入試に直結する単元であることが多く、そこで苦手だな、と感じる単元があればなるべく早めに克服しておくことが非常に重要になってきます。

今回は４年生、５年生で苦手になりやすい要注意単元を中心に、各学年での学習のポイント、それらの攻略法などを解説します。一度つまずくと取り戻すのに時間がかかってしまう受験算数、つまずかないためにも克服すべき重要ポイントを知っておきましょう。

Contents

1 ４年生の要注意単元と攻略ポイント
2 ５年生の要注意単元と攻略ポイント
3 自信を持って次学年の学習に取り組む

４年生の要注意単元と攻略ポイント

４年生では、受験算数の基礎基本を学習します。特に後半では、小数や分数の計算にはじまり、かけ算、わり算、単位換算などが出てきます。これらは計算の基本であるだけでなく、文章題においても知っていなければ解けない重要単元だと言えるでしょう。

これらの単元は、５年生で学ぶ重要単元である割合や速さ、平面図形といった入試の頻出単元の土台となる内容になっています。つまり、４年生で学習する内容が５年生の学習の基礎となり、さらには入試本番で要求される算数力の基本となっていくのです。

小数や分数、単位換算などは、大人から見ると当たり前のことで、間違えることを理解できないかもしれません。しかし、お子さんにとってみればはじめて学習する単元であり、そもそもの概念から理解しなければならないので、実は非常にハードルが高いのです。どの単元も初出の場合同じことが言えますが、特に小数や分数、単位換算は理解するのに時間がかかることが多く、十分な理解がないと計算問題から文章題に至るまでぼろぼろと落としてしまうことになりかねません。

そこで、これらの単元については特に注意して学習をていねいに行うことが重要だと言えます。

＜４年生後半の克服すべき要注意単元＞
・小数どうしのかけ算・わり算
・倍数と約数
・分数の計算

これにプラスして、各単元で学習する内容に単位換算が絡んでくるものは特に要注意です。いずれの単元も計算問題単体としての出題だけでなく、模試や入試本番で、さまざまな形式で出題されることが多いです。４年生で学習するタイミングで、着実に理解を深め、自由自在に使いこなせるように習得することが大切です。

それぞれの単元について、学習ポイントと攻略法を見ていきましょう。

小数どうしのかけ算・わり算：小数点のうち間違いに注意

小数どうしのたし算・ひき算は、４年生の前半でまず学習します。また、小数×整数、小数÷整数といった片方が少数のかけ算、ひき算についても学習しますが、ここまではそれほど苦労せずに学習を進められたという受験生の方も多いのではないでしょうか。

しかし、小数どうしのかけ算、わり算となると、急にハードルが上がり、つまずいてしまう受験生は少なくありません。それはなぜなのでしょうか？一番多いつまずきは、「小数点のうち間違いをしてしまう」ことです。小数どうしのかけ算やわり算をするときには筆算をすることも多いでしょうが、小数点の位置を間違えてしまい、本来ありえない計算結果を答えにしてしまうことが非常に多く見られるのです。

中学校にもよりますが、中学入試の計算問題では、文章題と異なり解答だけを答案に記入する形式が主流です。つまり計算のプロセスが合っていたとしても小数点の位置を間違えてしまい、その答えを書き込んだ時点でアウトなのです。計算問題で失点するのは模試でも一番やりたくない間違いだということはどのご家庭でも共通することでしょう。ですが、小数点のうち間違いは計算ミスの代表格なので、早めに対策し、間違いを撲滅しておくことがとても重要です。

小数どうしのかけ算の場合、小数点より右側に数字がいくつあるか、ていねいに数える習慣を身につけましょう。慣れると素早くできるようになります。その際に、最初に問題を見て、もとの数字より解答が小さくなるかといったアタリをつける数量感覚も身につけておくことがとても重要になってきます。

一方、かけ算より非常に多くの受験生がつまずいてしまうのが「小数どうしのわり算」です。わり算はもともと整数計算でも間違えやすい傾向が見られますが、特に小数の場合、基礎基本がしっかり身についていないと間違いを繰り返してしまうので注意しましょう。

小数どうしのわり算のポイントとして意識しておきたいのは、以下の２点です。

1.まずはじめに「割る数」が整数になるまで、割る数と割られる数の「小数点の位置」を動かすこと
2.計算して余りが出る場合は、割られる数のもとの位置から小数点を下ろすこと

小数どうしのわり算をするときにミスが起きやすいポイントは、「余りの小数点のうち間違い」です。これは計算問題を多く解いて習慣づけていくことによって克服していくしかないのですが、うち間違いを防ぐためには、日常的な計算練習をするときから、「たてと横をまっすぐそろえて」筆算を書き、計算していくことが非常に重要です。雑に筆算してしまうお子さんの場合、筆算を斜めに書いてしまうことも多いです。整数計算ならまだ何とかなるかもしれませんが、小数の場合は小数点をうつという作業が必要になるので、桁を間違えれば必ず計算結果も間違いになってしまうので注意しましょう。

もしなかなかまっすぐそろえて計算できないクセがついてしまっている場合は、マス目のついている方眼のノートを利用して計算練習してみることをおすすめします。間違いを克服するためにどのような道具を使っても恥ずかしいことはありません。使えるものは使って克服しましょう。

４年生の時点で小数点に対する意識をしっかり持っておく＝雑に計算しないということは、５年生になったときのさまざまな計算問題においても計算ミスを大きく減らすことができます。桁数が増えれば筆算をする機会も当然増えますので、家庭学習においても筆算はていねいに書くように心がけて攻略しましょう。

倍数と約数：普段の生活で感覚を養うのがポイント

倍数や約数は、それだけ見ると難しいことではありません。倍数を出すこと自体は無理なくできる受験生がほとんどです。約数は少し数量感覚が必要ですが、それでも素数（１とその数字以外に約数がない数）を覚えておけば、もったいない失点は防げるでしょう。

また、単なる倍数、約数ではなく公倍数、公約数、最小公倍数、最大公約数などさまざまなバリエーションがありますが、これらも桁数がそれほど大きくなければていねいな書き出しを行うことによって答えることは可能です。ポイントになるのは、いかに素早く、また正確に倍数や約数を導き出せるか、ということです。

実際の入試問題では、倍数や約数を使って解く問題が非常に多く出題されます。なかでも「分数の計算」では、最小公倍数、最大公約数を使うことが非常に多くなるので注意が必要です。入試の制限時間は非常に厳しいものですから、倍数や約数をすばやく正確に導き出すことができないと時間切れになってしまうことも少なくないのでやはり事前のしっかりしたトレーニングが重要になってきます。

倍数や約数を素早く正確に導き出すためには、計算問題の練習で意識することがもちろん一番大切なのですが、日常生活のなかで、数字を見かけたら倍数や約数を頭の中で導き出してみる練習も意外に効果的です。倍数や約数を導き出すには習慣化がなによりも大切であり、そのためには数量感覚を養うことが欠かせません。机に向かう以外にも、生活の中でそういった数量感覚を養うのもおすすめです。

たとえば、塾の行き帰りの道で、見かけた車のナンバープレートに書かれた数字を使って最小公倍数や最大公約数を暗算してみるなどは気楽にできますね。もし保護者の方が車で送り迎えをする場合は、「あ、ナンバープレートだ」と声がけをして、お子さんに倍数や約数を導き出すよう促すのも良いでしょう。

また、携帯電話はいまや生活必需品ですよね。家族の携帯電話番号を使って、ゲーム感覚で倍数や約数を出してみるのもおすすめです。スーパーやコンビニに買い物に行ったときなどに商品の値段を見て倍数や約数を暗算してみるのも良いですね。

分数の計算：加減と乗除の区別が重要

分数の計算も小学生にとっては関門のひとつです。倍数や約数を学習したあとにカリキュラムに出現してくるのが、「異なる分母のたし算・ひき算・かけ算・わり算」です。一つひとつの計算自体は実は決して難しくはない単元なのですが、分数を使って四則計算を一気に学習するところにつまずきポイントがあります。

四則計算をしっかり使い分けられているお子さんは問題なくできるのですが、４年生の段階では四則計算に不安が残るお子さんも少なくありません。さらに分数が入るため、解き方を混同してしまうということも怒り得るので注意が必要な単元なのです。

たとえば、分数のたし算、ひき算のばあい、分母どうしと分子どうし、どちらを足したり引いたりするのか迷ってしまうケースが少なくありません。また、分数のかけ算やわり算の場合、分母の最小公倍数をとってから解くのかどうなのか、といったように、たし算・ひき算と、かけ算・わり算によって解き方が異なるのですが、この解法を反対に覚えてしまい、間違い続けてしまう受験生も非常に多いので要注意ポイントです。

このようなもったいない間違いを防ぐためには、分数の計算を学習したら、できるだけ毎日分数の計算練習をすることが大切です。もし分数の計算が苦手な場合は、最初のうちは１問に時間をかけても構いません。何よりも大切なのは、分数の計算の法則を理解し、できるようにすることです。そのためには理解が不十分なのに急がせて多くの問題を解かせることは避けたほうが賢明です。間違いばかりが積み重なり、自身を失ってしまうからです。

最初のうちはある程度時間をかけてもいいので分数の計算、四則計算の基礎をしっかり理解し、徐々にスピードを上げて練習を積んでいきましょう。分数の計算問題は、分数だけではなく整数、小数、分数が入り交じった計算問題、四則が混合した計算問題も良く出題されます。難易度が上がるように思えるかもしれませんが、計算の法則を守り、練習を積むことで正答率を上げることは十分可能です。あきらめずに克服すべく、計算練習をしっかり行いましょう。

５年生の要注意単元と攻略ポイント

５年生で学習する内容は、中学入試の核となる単元が集中しています。つまり、５年生で学ぶ内容がどれだけ定着しているかが６年生での学習に影響し、ひいては入試本番でも結果を分けると言えるのです。

単に単元が頻出だというだけでなく、学ぶ内容、解法、法則などをほかの単元でも利用することが増えるのが５年生の学習の難しいところです。一つひとつの単元をしっかり理解し、違う単元で考え方を使うときに「これを使えば解ける」と使いこなせるようになるまでにしておくことが重要です。

５年生で学習する内容で、特にしっかり力をつけておきたい要注意単元は以下の３つです。

＜５年生後半の克服すべき要注意単元＞
1.速さ
2.比
3.合同と相似

速さ：単位換算と条件の図示が重要

速さの単元は、中学入試で再頻出の単元と言えるでしょう。ほとんどの中学校でなにかしらの形で速さの単元の理解を問う問題が出題されています。そのような重要単元なのですが、苦手とする受験生は少なくありません。範囲が広いことに加え、覚えなければいけないこと、解法が多いことから混乱してしまうことがその原因として挙げられます。

ですが、入試で頻出単元と言えば、なんとか克服したいですよね。そこで、速さの学習の際に攻略するポイントとして、単位換算を自由自在に行う「単位の修得」、そして問題文の条件（状況）を自分で図を描く「図示」が非常に重要なのでできるようにしておきましょう。

単位換算は速さの基礎中の基礎！

まず「単位換算」ですが、速さの３条件である「速さ」「距離（道のり）」「時間」のそれぞれについて、単位をしっかり押さえましょう。単に公式に数字を当てはめると最後にどの単位をつけるか迷ってしまい、間違いに繋がりやすいので、単位をつけながら計算できるようにすることが重要です。

それぞれの単位換算が自由自在にできないと、考え方は合っていたとしても最後の計算で間違えてしまいます。また、設問で速さを聞かれているのか、距離を聞かれているのか、はたまた時間を聞かれているのかを混在してしまいかねません。そうすると、せっかく解法を理解できていても不正解になってしまいます。そういうことを避けるためにも、単位をしっかり押さえておくことは速さの学習に置いて重要な攻略ポイントです。

状況図を描いて問題を整理しよう

単位換算の基礎基本をしっかり押さえることと同時に、速さの問題を解くなら必ずやらなければいけないのが、問題文の内容を簡単な図（状況図）を書いて整理することです。出てくる登場人物（Ａさん、Ｂさん）やその動き（いつ出発、どの方向に歩くまたは走る、など）を簡略な図にするのです。

速さの図と言うと「ダイヤグラム」を思い浮かべるかもしれません。実際に、速さの図を描こうとしてダイヤグラムを描く受験生も多いのですが、これはグラフの一種であり、描くのに非常に時間がかかります。もちろん設問でダイヤグラムの空白部分を埋めなさい、という問題が出された場合は書く必要がありますが、そういう場合でもない限り速さの問題で一からダイヤグラムを描こうとするとまず時間制限に間に合わないでしょう。

そこで、うまく活用したいのが状況を簡単に図示した状況図です。たとえば、以下のようなものです。

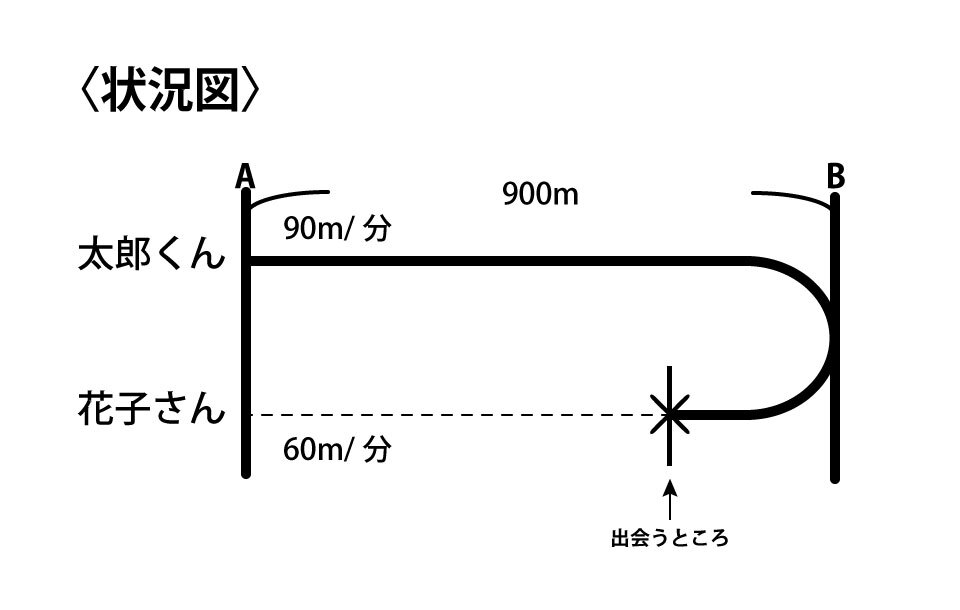
この図のような簡略化したもので大丈夫です。大切なのは、出題されている内容を素早く正確につかむことです。条件などを簡単に書き込んで図示することで、問題の内容を素早く正確につかむ練習を積むことが大切です。速さの問題に限らず受験算数では手を動かして図を描くことがとても大切です。ぜひしっかり図示できるように訓練しておきましょう。

比：比で表されているものに単位をつけてわかりやすくする

比を使う問題も、中学入試では必ずと言っていいほど頻出の単元です。比の計算自体はそれほど難しくないのですが、比を「使う」というところが要注意ポイントです。図形から特殊算、ありとあらゆる問題で比が使用されることが多いため、「どのように比を用いるか」という視点が非常に重要になってくるのです。

なぜ比が苦手になるのか

比の計算自体は、かけ算やわり算ができれば理解できる、比較的単純なものです。そのため、比を習い始める時点では、どの受験生も簡単だと感じ、意欲的に取り組もうとします。しかし、長い文章題で比が用いられているものになると途端に解けなくなり、比に対して苦手意識を持つようになってしまうのです。比という考え方自体が、お子さんにとっては少し抽象的でわかりにくい概念だということも比に対する苦手意識を助長する一因となっています。

比に単位をつけてみると一気にわかりやすくなる！

このように苦手な受験生が多い比を使った文章題ですが、問題をわかりやすくするために、「比に単位をつけること」をおすすめします。たとえば、「りんごとみかんが５：３あります」という問題の場合、「りんごが５個、みかんが３個あります」というように単位をつけて読み替えるのです。

お金についての比の文章題も多いですが、たとえば「姉と妹のお小遣いは７：５です」という問題であれば、「姉のお小遣いは７円、妹のお小遣いは５円」と考えがちですが、お小遣いが７円、５円というのは現実的ではないですよね。そこで「姉のお小遣いは７００円、妹のお小遣いは５００円」ともっとイメージしやすいように変えてみても良いでしょう。

このように比に単位をつけてみると、問題文の内容が具体的に見えてくるので、その問題の「状況」がどのようなものなのかがつかみやすくなります。そして、比がどのように扱われているのか理解しやすくなります。こういった単位をつける、ということは家庭学習で比が出てきたときに気軽にできることです。もし、比の文章題を解いているときにイメージがつかめずにお子さんが悩んでいたら、ぜひ「単位をつけてごらん」と助言してあげてください。考えが一歩先に進められますよ。

合同と相似：まずは基本図形を見つけるところから

５年生の学習単元として速さ、比は非常に重要です。そして、比はほかの単元や図形、文章題ありとあらゆるところにその後出てくる非常に重要な考え方です。このように比を学習したあとに押さえておきたい最重要単元として、「合同と相似」があります。受験カリキュラムでも、比を学習したあとに、図形と比を絡めた合同と相似が設定されています。

中でも「相似」は入試の頻出単元であり、図形と言えば相似と比、というくらいです。それだけに苦手意識を持つ受験生が多い単元でもあります。だからこそ「相似」を制する者は受験を制するというほど重要単元だと言えるでしょう。

ピラミッド型とクロス型を理解しよう

そんな相似をしっかり習得するためには、２つの基本図形を覚えることが何より重要です。それは「ピラミッド型」と「クロス型」の２つです。塾によってはＡ型とＸ型と呼ぶこともありますが、図形の形に２種類あり、形も同じなのでしっかり覚えましょう。

まずはこの２つの形、そして対応する辺の位置をしっかり覚えましょう。特にピラミッド型は、対応する辺の位置を間違えやすいパターンなので、覚える際には注意してください。

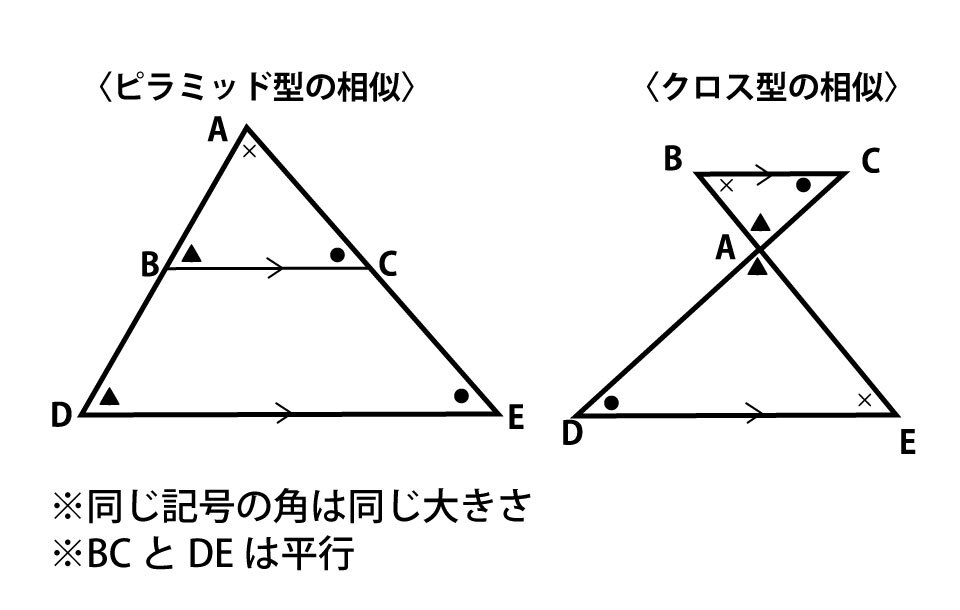
２つの形を覚えたら基本図形を見つける訓練を

ピラミッド型とクロス型をしっかり押さえたら、次に基本図形を見つける訓練をしていきましょう。たとえばクロス型の場合は、直線が交わっている箇所を見つければいいことがわかるので、見つけるのはそれほど難しくありません。ただし、ピラミッド型は少々難関だと言えるでしょう。苦戦する受験生も非常に多いところです。ピラミッド型を見つけ出すポイントとしては「平行線と三角形」を意識して見つけることが挙げられます。ぜひ注目してみてください。

合同や相似といった図形の問題は、平面図形の問題だけとは限らず、立体図形の問題でも絡めた形でよく出題されます。いずれの場合でも、基本図形を見つけ出し、解法のヒントを見つけていくことは同じです。最初は易しめの単純な相似の問題をしっかり理解できるようにし、徐々に応用的な問題にチャレンジしていきましょう。

入試の相似の問題は一見して基本図形が見つけられないような問題もあります。そこでは補助線をひいたりしながら自分で手を動かして相似形を見つけていくことになります。そういった難易度の高い入試問題に抵抗なく取り組んでいくためにも、相似の基本図形をしっかりマスターし、手を動かしながら学習することを心がけていきましょう。

自信を持って次学年の学習に取り組む

４年生、５年生の特に後半で学習する重要単元について、要注意ポイントと攻略法をご紹介しました。４年生で学習する単元は５年生で学習する受験算数の基礎です。そして学習は続き、５年生で学習する速さや比、相似といった単元は入試本番に直結しています。そのため、各学年に配置されている要注意単元をしっかり理解し、使いこなせるように訓練し、自信を持って次の学年の単元に取り組めるように準備しておくことが何よりも重要だと言えるでしょう。

今回ご紹介した要注意単元は、克服しなければ受験学年の学習に支障が出てしまうほどの重要単元です。出てきたときにしっかり理解しておき、次の学年で出てきたときに基礎基本を思い出して理解をさらに深められるよう、出てきた単元はひとつずつクリアにして行くよう意識して学習を進めていくことが重要です。

４年生の学習単元では毎日の計算練習が重要です。計算は受験算数の基礎であり、避けて通ることはできません。すばやく正確な計算力が受験算数の基礎基本と言っても過言ではないでしょう。また、５年生の速さや比、相似などの要注意単元を学習する際のポイントは「手を動かして」勉強することです。複雑な条件が問題文に入ってくることも少なくないため、その内容を単純化して簡単な図に描いてみると、最初はとっかかりすら見つからなかった問題を解くきっかけが見つかることはたくさんあります。

４年生、５年生で学習する内容は、自信を持って次の学年の学習内容に立ち向かえるようにするための準備運動とも言えるものです。決して手を抜かず、出てきた単元は出てきた都度理解し、わからないところは放置せずに塾の先生や個別指導などで質問し、潰しておきましょう。

わからないところをわからないままにしておくと、受験学年になって穴だらけということになりかねません。そうすると過去問演習もスムーズにできなくなりますし、模試などの成績も下がってしまいます。そういうことにならないためにも、要注意単元は意識して、早め早めに克服していくことが大切です。ぜひ、普段の学習でも意識しながら学習していきましょう。

＜関連記事＞