今回の記事では様々な立体のうち正多面体の注目し、その秘密を探っていくコラムのような内容になっています。受験で登場する図形の問題を解くためには、その土台となる図形の性質への理解が重要です。そのためここでは小学生が疑問にしやすい、正多面体が5つしかないことの理由などを交えながら、単元の内容を解説していきます。
多面体とは?
では今回の記事で正多面体を取り扱うにあたって、その前提知識として多面体とは何かについて解説していきます。簡単に言ってしまえば多面体とは4つ以上の多角形に囲まれた立体のことです。そして多角形とはいくつかの線分で囲まれた図形のことを指すので、つまり平たく言えば、多面体もたくさんの線分に囲まれた立体だとみなせるわけです。実際そのようなイメージで捉えている人がほとんどだと思われます。そして多面体の名前についても、いくつの平面図形で構成されているかで○面体と呼ぶことはほとんどの人が理解していることでしょう。
そのためここではもう少しステップアップした理解を目指していきましょう。ここでは腕見た定義の「多角形に囲まれた」という部分と「4つ以上」という部分に注目し、話を続けていきます。まず前者の「多角形に囲まれている」についてですが、これは裏を返せば多角形でない図形が組み込まれていれば、それは多面体だとは言えないわけです。では多角形でない図形とは何でしょうか。それは円やおうぎ形といった丸みを帯びた図形のことです。先で確認したように、多角形は線分で囲まれた図形でした。この線分とはある点からある点までまっすぐ引かれた線のことを指します。ゆえに点と点が繋がれていても、それがカーブしていては「線分」の定義にあてはまらず、円やおうぎ形は多角形とみなされないため、円柱や円すいといった図形は多面体の仲間には含まれないのです。
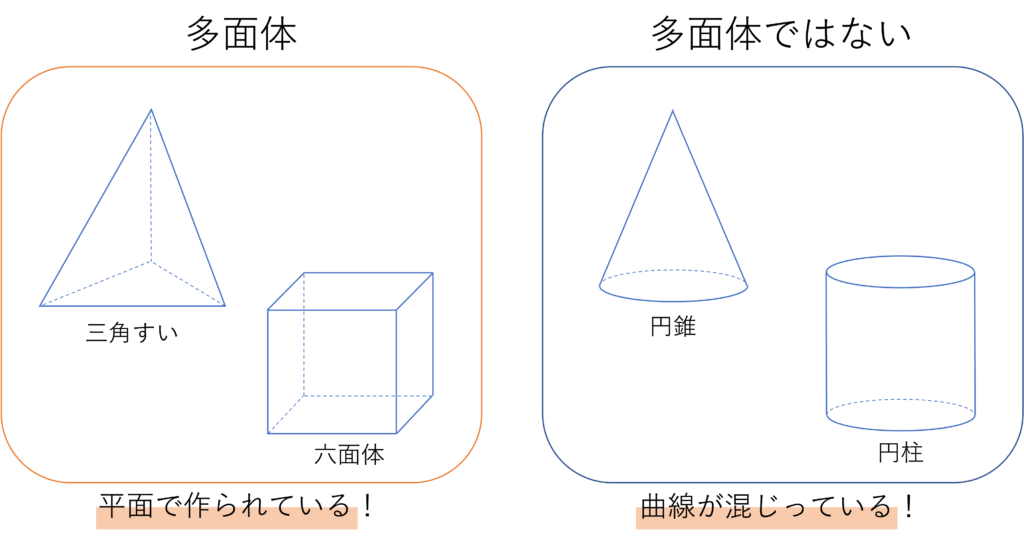
続いて「4つ以上」という部分に注目していきましょう。上で確認したように、多面体作られるには4つ以上の多角形が必要です。その理由は立体というものが底面と頂点で作られるからです。まず底面ですが、すべての多面体の面は多角形になっているので、当然底面も多角形です。そして多角形とは3つ以上の辺で作られるものなので、多面体とは少なくとも3つの辺と1つの頂点を繋いだ形になるわけです。ここで頂点と底面をつなぐ面について考えてみると、少なくとも1つ目の辺と頂点を結ぶ面・2つ目の辺と頂点を結ぶ面・3つ目の辺と頂点を結ぶ面の3つの面が必要になり、そのため底面+底面と頂点をつなぐ3面という構成で、最小でも4つの面がないと多面体は作られないわけです。
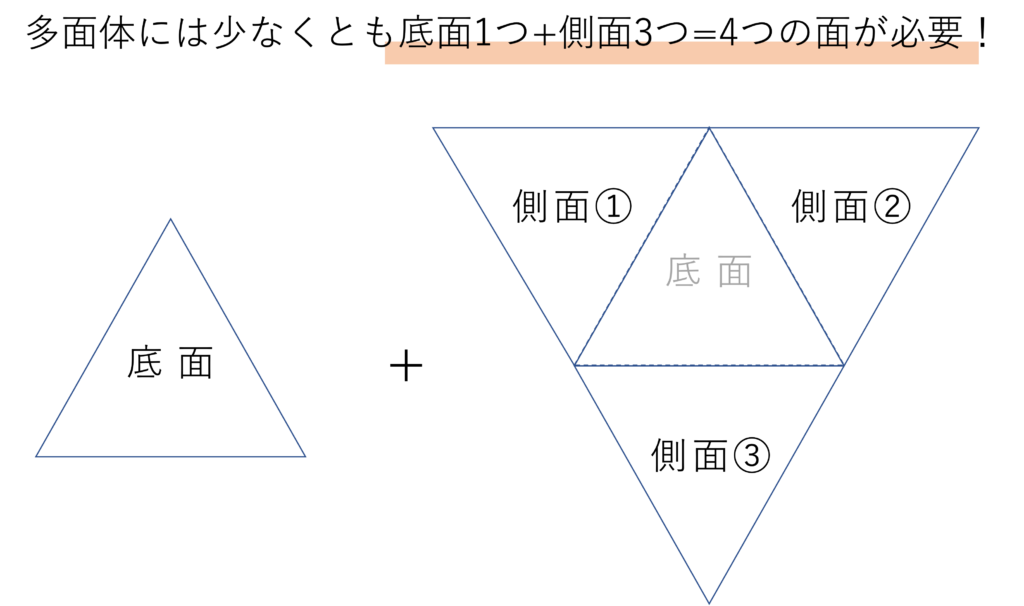
ただしこれも、円すいや円柱といった多面体以外の立体は例外になるわけです。例えば円すいだと、展開したとき面の数は側面が1つと底面が2つの合計3つになりますし、円すいは側面が1つと底面が1つの合計2つになりますね。このように多面体とそうでない立体の違いも覚えておくといいでしょう。
「正」多面体とは?
ではここからは多面体の中でも正多面体について見ていきましょう。正多面体とは、すべての面の形が合同な正多角形である多角形を指します。そして正多角形とは多角形のうち、すべての辺の長さが等しくすべての角の大きさも等しい多角形のことでした。つまり正多面体も全ての辺の長さが等しかったり、また全ての面における角の大きさが等しかったりするわけです。この正多角形ですが、全ての面が合同であるという条件がとても厳しいので当てはまるものは5つしかありません。その中身は正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類になります。特に覚えておきたいのは、それぞれの図形の面の数・頂点の数・辺の数・面の形の4つです。5つの正多面体における各要素は以下の表のようにまとめられます。
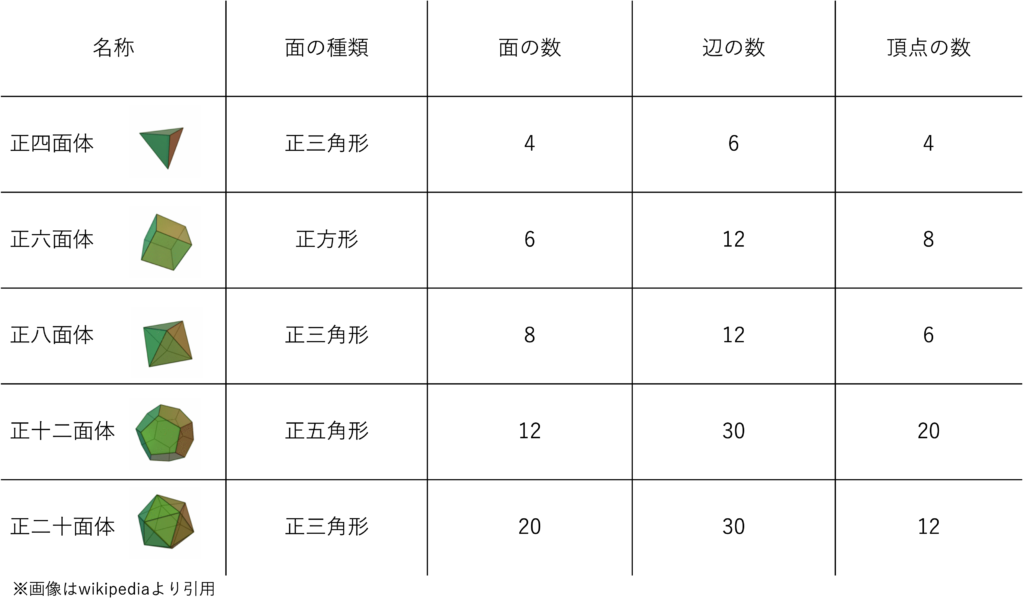
ここで意識しておきたいのは、面の数と面の頂点の数が違うということです。普通の多面体でも面の数と面の頂点の数は異なります。例えば六面体があったとして、そこに「6」という数字があるからといって、すべての面が六角形になるなんてことはないわけです。例えば下のようなすい状の六面体の場合、底面は五角形でそれ以外の面は三角形になっていますよね。
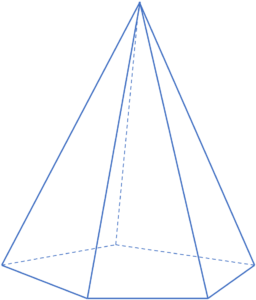
しかし全ての面の形が同じである正多面体だと、「正四面体の面の形は正四角形だ」とか「正六面体の面の形は正六角形だ」といったように誤解してしまう人が多いのです。ちゃんと図を見たり頭で考えたりすれば解決することなのですが、言葉の印象でつい間違えてしまいがちですので、その辺りの誤解を解くという意味でも図形に触れる機会を増やすことが重要だと言えますね。
なぜ5種類しかない?
ではなぜ正多面体は5種類しかないのでしょうか。その理由は正多面体を平面に展開したときのことを考えると見えてきます。すべての立体は辺で切っていくと展開図という形にすることができるのですが、逆に言えば展開することのできない図形は組み立てても立体にならないのです。
ここで、この展開できないと立体にはならないという前提をもとに、正多面体の角を見ていきましょう。上で取り上げた5つの正多面体でもそうでない図形でも、立体では1つの角に少なくとも3つ以上の面が集まっています。そのためここまでのことをまとめると、頂点に3つ以上の図形が存在して展開図から組み立てることのできるようなものであれば、立体図形として成立するというわけです。
そして正多面体とは正多角形で作られた図形のことでした。したがってここからはいくつかの種類の正多角形を頂点に集めてみて、図形が完成するかを見ていきましょう。まずは一番小さい単位として、正三角形を3つ集めてみます。この展開図は別の頂点にもう1つ正三角形を足すことで正四面体になりますね。
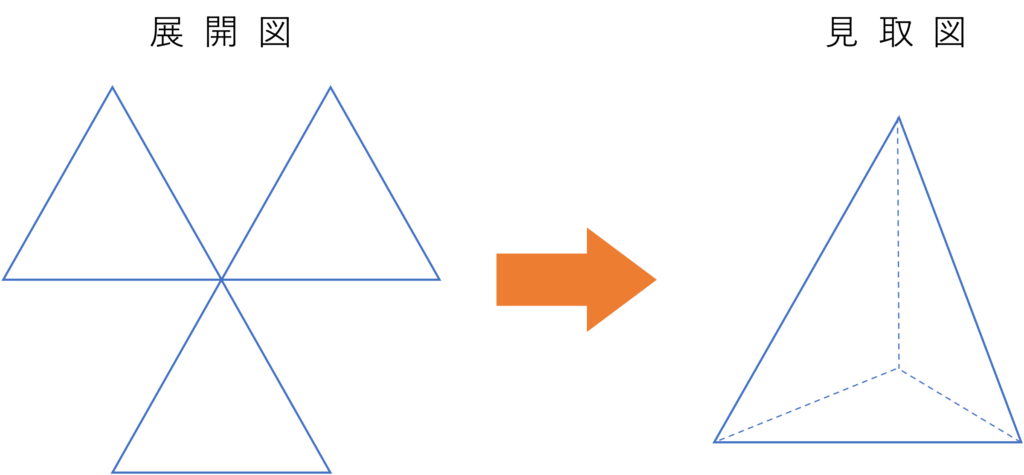
次は正三角形を4つ集めてみましょう。この図形は別の頂点にも2つずつ正三角形を足していくと正八面体になります。
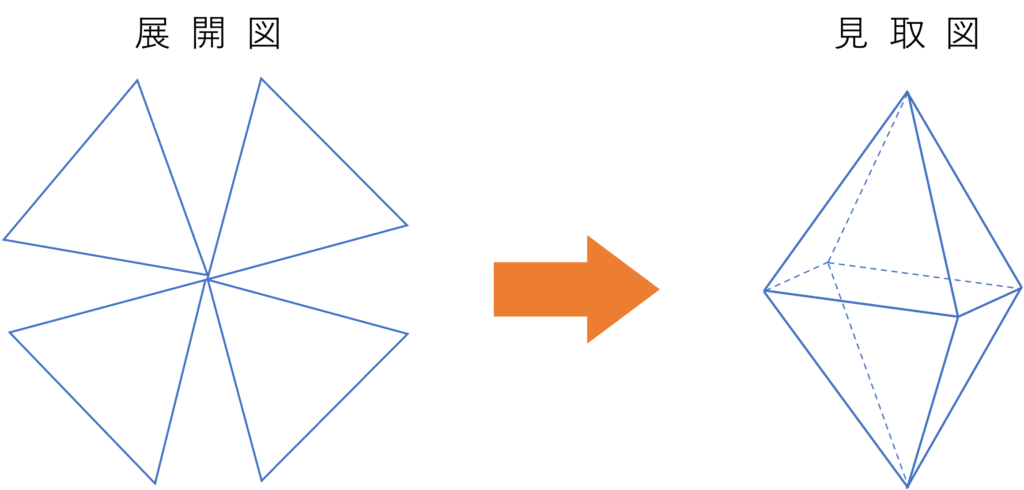
続けて正三角形を5枚集めてみます。この図形は別の頂点にも3つずつ正三角形を足していくと正二十面体になります。
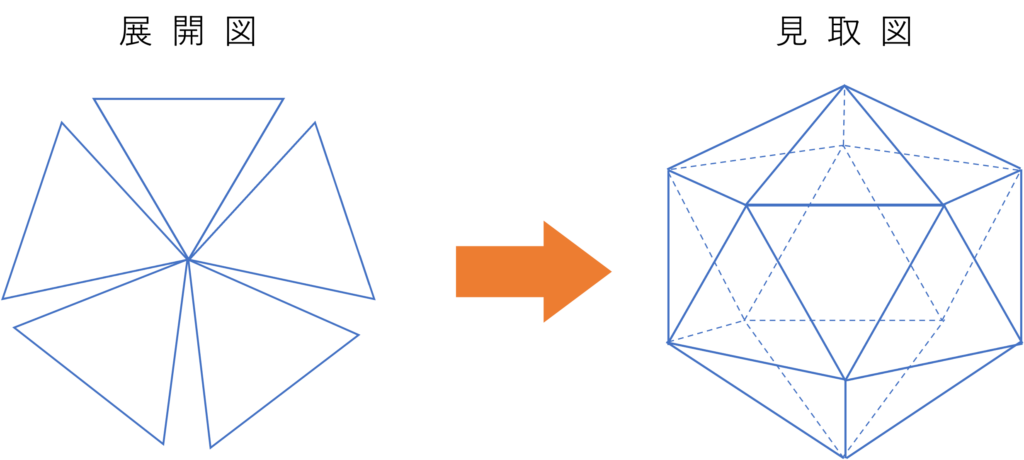
そしてここで正三角形を6枚集めてみます。正三角形の1つの内角は60°なので展開図上で1つの頂点に6つの正三角形を並べることはできるものの、360°ぴったしで図形が配置されているので、このまま組み立てることは不可能ですよね。このように1つの角に集まっている図形の内角を足した和が360°以上になると、その図形の角は平らになってしまい組み立てることができなくなってしまうのです。
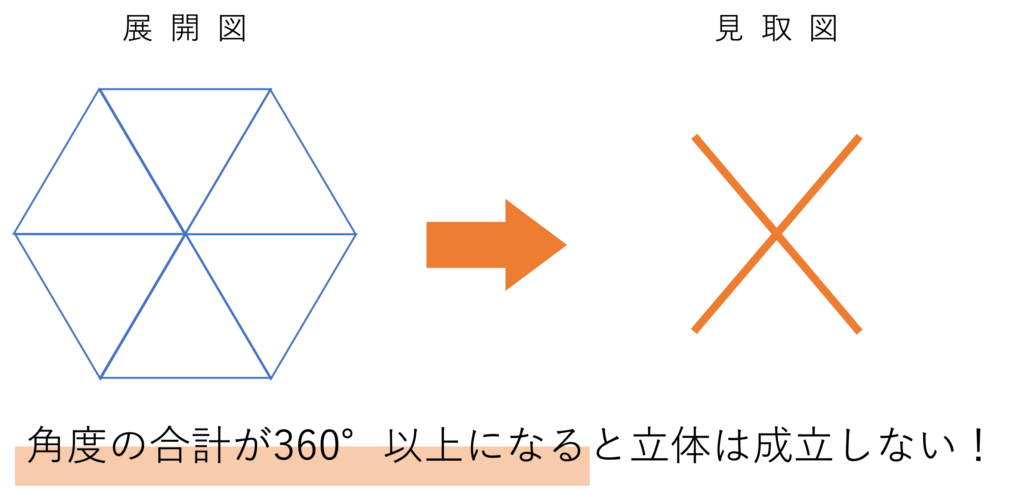
さて正三角形を集めるときの限界が5個だと分かったところで、次は正方形を集めてみましょう。まず1つの角に正方形を3つ集めてみます。この図形は別の頂点にも2つずつ正方形を足していくと、正六面体になりますね。
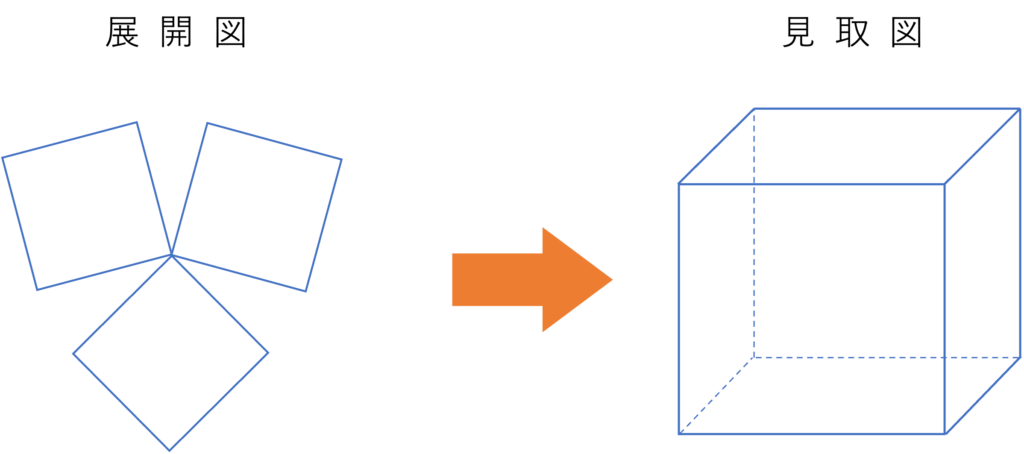
続けて正方形を4つ集めてみます。しかしこのとき、正方形の1つの角の大きさは90°なので1つの頂点に集まる角度の和は90°×4=360°になり、図形が組み立てられなくなってしまいますね。そのため正方形を集める限界は3つだと判断でき、これ以上の正多面体は正方形では作れないと判断できるのです。
同様の手順で次は正五角形を集めてみましょう。まず正五角形を3つ集めてみると、下の図のような展開図が出来上がり、これは他の頂点についても3つずつ図形を集めていくことで正十二面体となります。
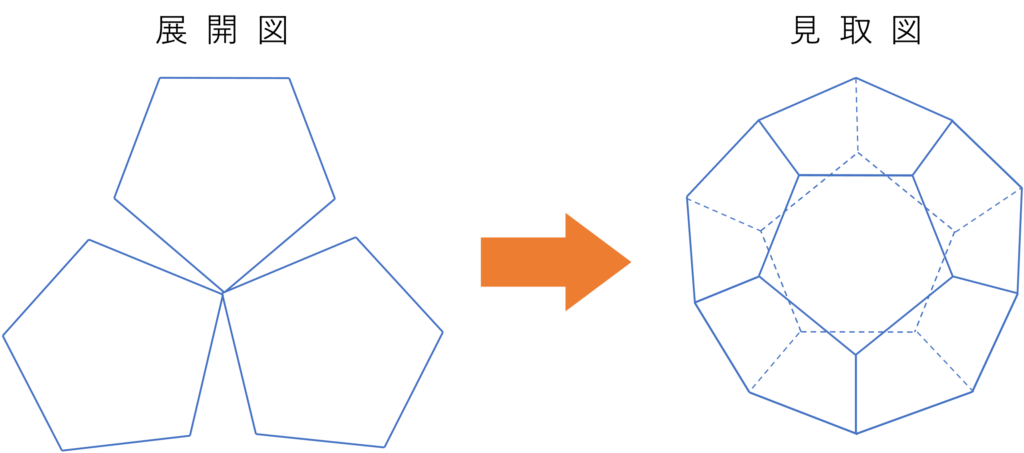
では続けて正五角形を4つ並べてみようといきたいところですが、正五角形の1つの内角は108°なので、4つ並べようとすると角度の合計は108°×4=432°となり、360°の平面上には表せないことになります。よって正五角形を集める限界は3つだということが分かりますね。
正五角形の次は正六角形、といきたいところですが、正六角形の内角の1つは120°なので3つ並べたところで360°となってしまい、いきなり組み立てることができなくなってしまいますね。このように正六角形以上の正多角形だと、1つの内角が大きすぎて3つ以上並べることができないのです。そのため正多面体は5つしか成立せず、5種類しかないというわけですね。このような理由が受験に登場するわけではないですが、ちょっとした疑問の解消から単元への解像度が上がることが大幅に上がることもあるので、頭の片隅に入れる努力をしてみるといいでしょう。
知識の確認
最後に簡単な問題を出したいと思います。ぜひ知識の確認に役立ててみてください。
【問題】
- 問1:正四面体の面の数は?
- 問2:正六面体の頂点の数は?
- 問3:正十二面体の辺の数は?
- 問4:正二十面体の頂点の数は?
【模範解答】
- 問1:4
- 問2:8
- 問3:12
- 問4:12
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

終わりに
今回の記事では子どもが疑問を持ちやすい正多角形に注目し、その基本的な定義から応用的な知識まで解説していきました。図形の問題は慣れるまで解きにくいでしょうが、まずは少しずつ図形を見る・図形に触れることを増やしていき、柔軟に問題を解くための知識を身につけていくことを意識していきましょう。本記事が今後の学習のお役に立てば幸いです。
(ライター:大舘)


















