今回の記事では平面図形・空間図形における移動について取り扱っていきます。第1段目の本記事では基礎編と称して,移動にはどのような種類があるのかを簡単にまとめてみました。図形の移動の問題は頭を柔軟にして解く必要があり,それゆえ勉強量や慣れが大きく結果に作用してきます。そのため早めの対策が必要です。よろしければ周りと差をつけられるよう,一緒に学習していきましょう
図形・点の「移動」とは…?
まず図形・点が移動するとはどういうことでしょうか。移動とは簡単に言ってしまうと位置が移ることを指します。この言葉自体は日常生活でも使うものですので馴染みがあると思いますが,算数において移動という単語が出てきた場合,もう少し限定的な使われ方がされます。それは移動する前と後で形が全く変わらないということです。つまり移動にあたって変形が伴わない,ということですね。以下でご紹介するように向きが変わったり裏表が逆になったりすることはあるものの形が変わることは絶対にありません。そのことを意識しながら,次の3種類の移動を覚えていただけますと幸いです。
平行移動
まず1つ目に紹介する移動のタイプが平行移動というものです。これは図形を一定の方向に一定の距離だけ動かすことを指します。移動と言われておそらく一番イメージしやすいのがこの平行移動なのではないでしょうか。例えば次のような図形があったとして,この三角形を左下から右上に動かしていくような場合を平行移動と呼ぶことができます。
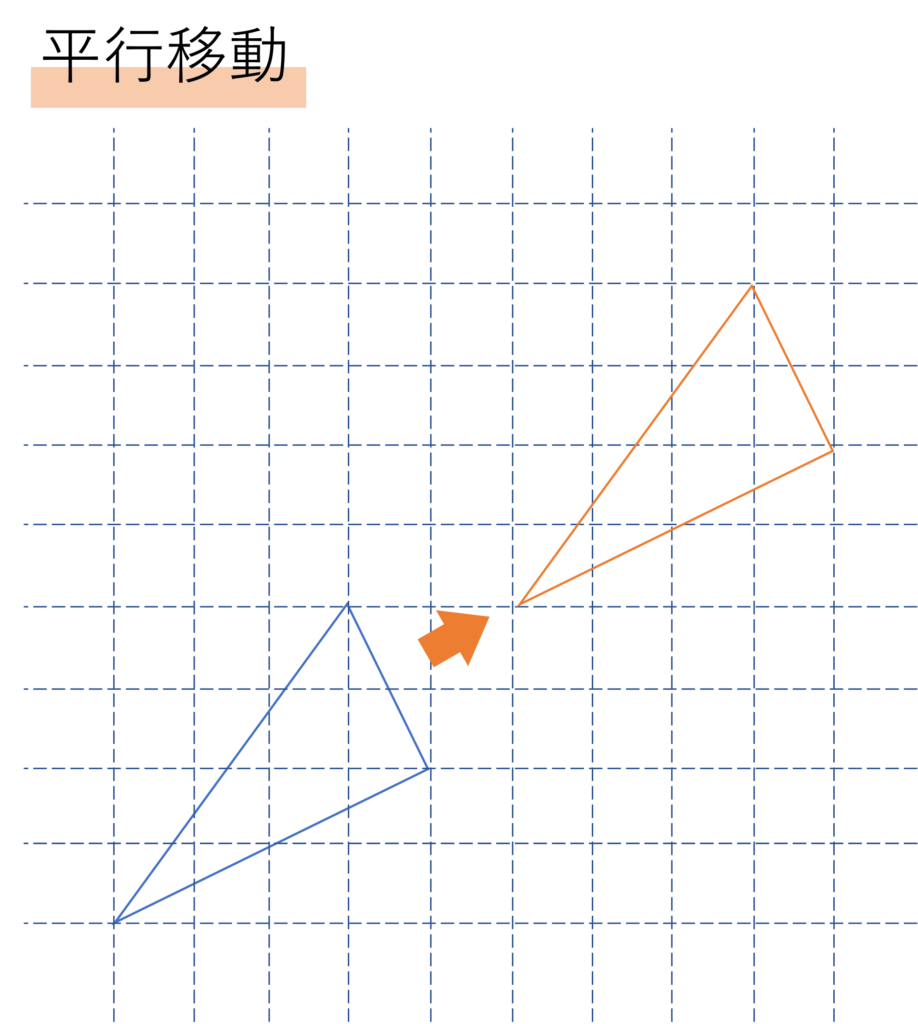
先ほどもご紹介しましたが,算数における移動とは形を変えずに位置を動かすということを意味します。この観点から上の図を見たとき,図形の形に一切変化がないことが分かりますよね。このように図形をただスライドさせるものを平行移動と呼ぶ,と覚えるといいでしょう。
なおここで図形が変形していないかを見分けるポイントとして,図形を構成するそれぞれの点を繋いだときどうなるかを考えてみるといいでしょう。今回は三角形なので3つの点が移動しているわけですが,この移動をつなぐと次のような図が出来上がります。
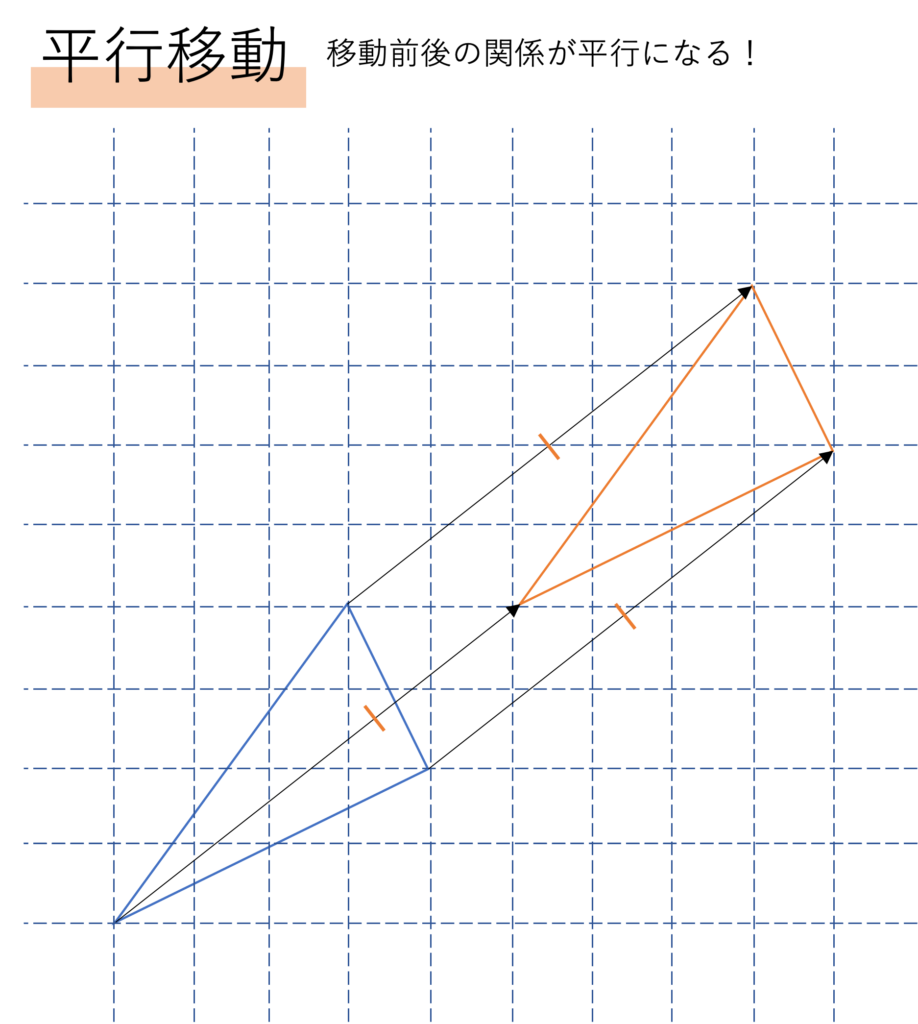
平行移動の場合,このように点同士を繋いでいくと全ての線分の長さが等しくなります。またそれだけでなく,方向も全く等しくなるため全ての線分が平行な関係におかれることになります。このことから図形をスライドするという平行移動の内容は,難しく言い換えると図形を平行に動かすということになりますね。今回はそれぞれの移動のイメージだけ掴めれば十分なのですが,このような細かい中身や定義も覚えておくといいでしょう。
回転移動
次にご紹介するのは回転移動です。これは図形の向きを変えるような移動のことを言います。この回転移動は一番図形の問題の中で登場しやすいものになります。例えば下の図において,左下のような図形を右上のように動かすことが回転移動の内容になります。
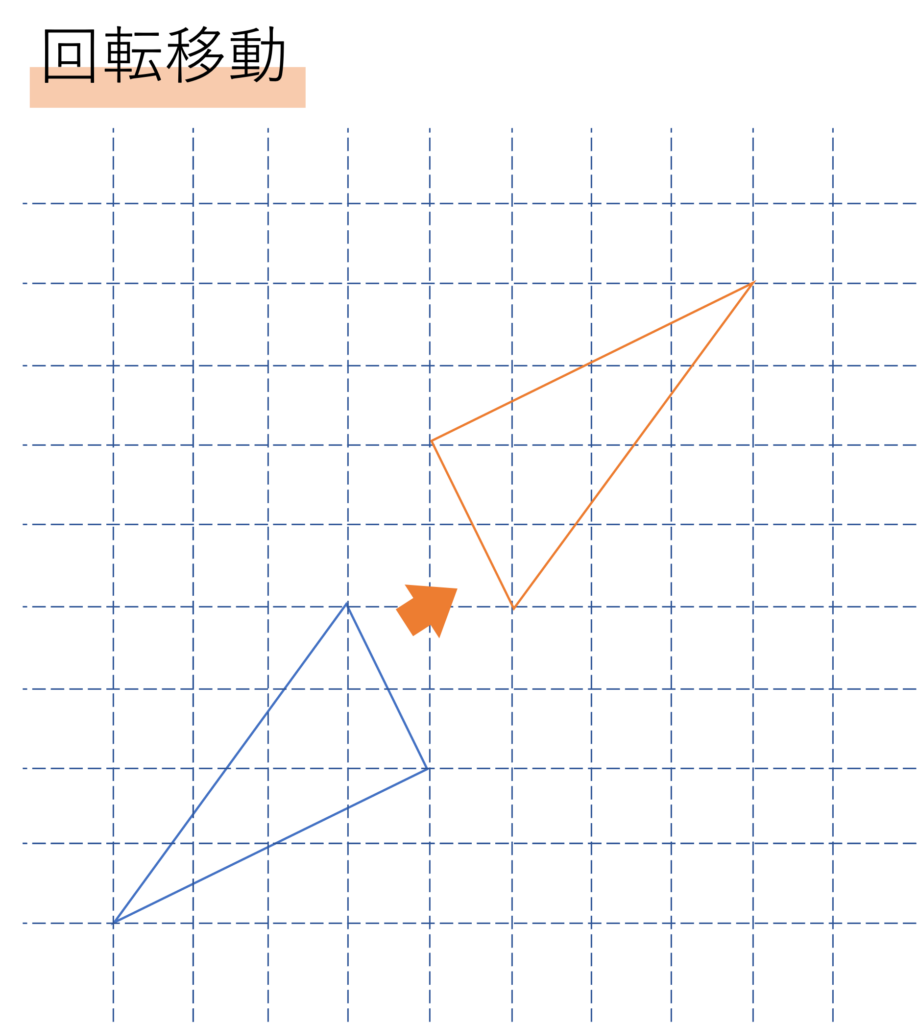
この回転移動でも,図形の向きこそ変わっていますが大きさや形は全く変化していないことを押さえておきましょう。そしてこの回転移動についても,移動前と移動後の点の動きに注目してみましょう。実はこの動きのなかに「回転」移動と呼ばれる理由があるのです。
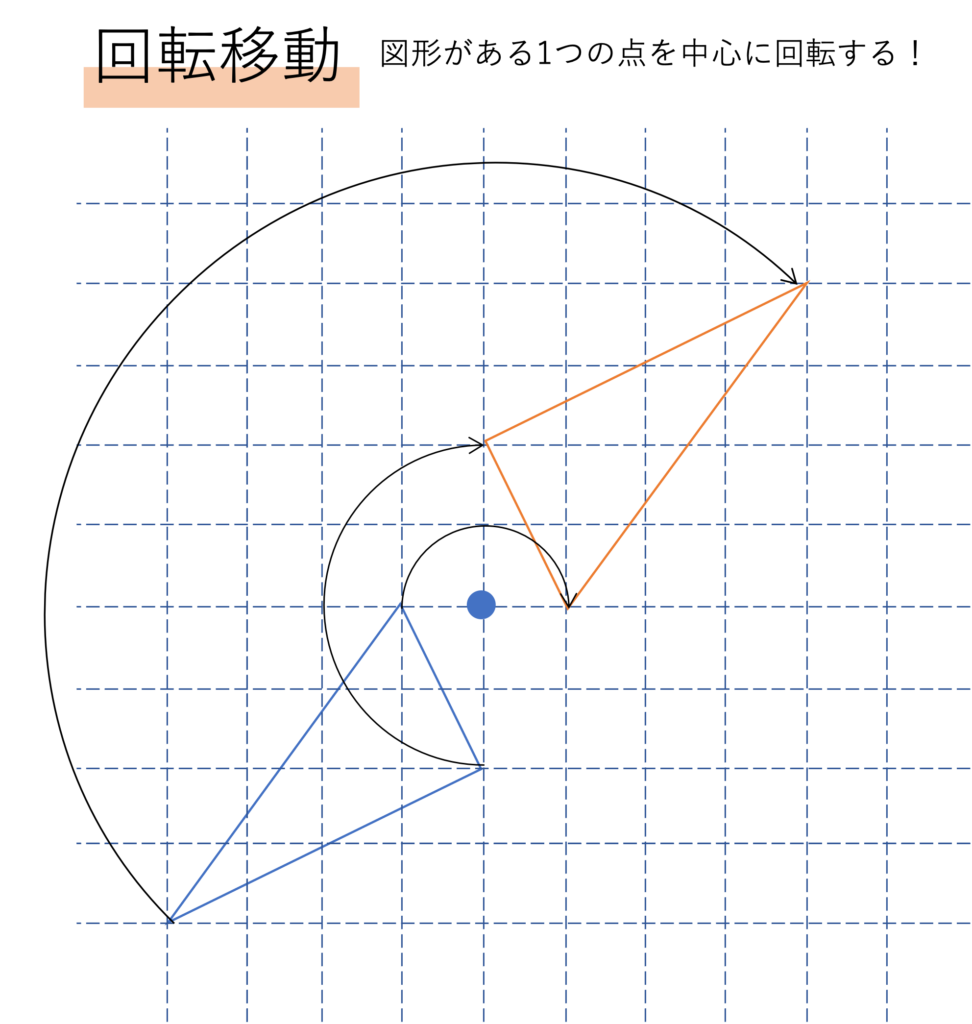
回転移動の場合,移動の前後の点を結ぶと円を描くような曲線ができます。この全ての曲線が1つの点を中心として描かれており,その様子から図形が1つの点を中心に回転すると言え,この動きが回転移動と呼ばれているわけです。ちなみにこのときの中心の点は,それぞれの点を直線で結んでいったときの交点になりますので,探すときに参考にしてみてください。なお受験ではこの回転移動のときに描かれる曲線が問題の対象になりますので,縁を描くことはきっちり覚えておきたいところです。
対称移動
最後にご紹介するのは対称移動です。この移動は,図形を鏡合わせになるように動かすことを指します。対称移動は中学受験において頻繁に登場するものではないですが,図形の折り返しという特別な問題においては必ず使われる移動です。一例を挙げると,左下の図形を右上に持っていくような移動が対称移動と呼ばれます。
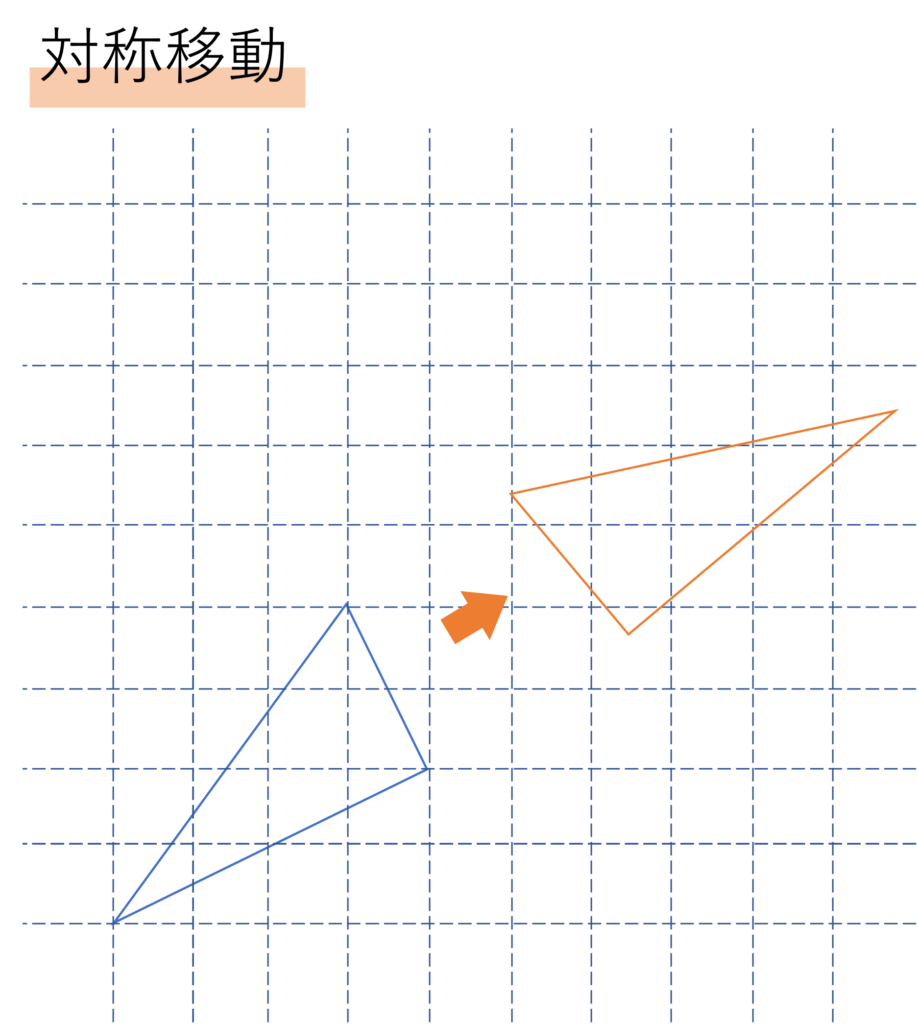
この対称移動でも,平行移動・回転移動と同様に図形のサイズや形に変化はありません。そしてこれまた同様に点の動きに注目してみましょう。
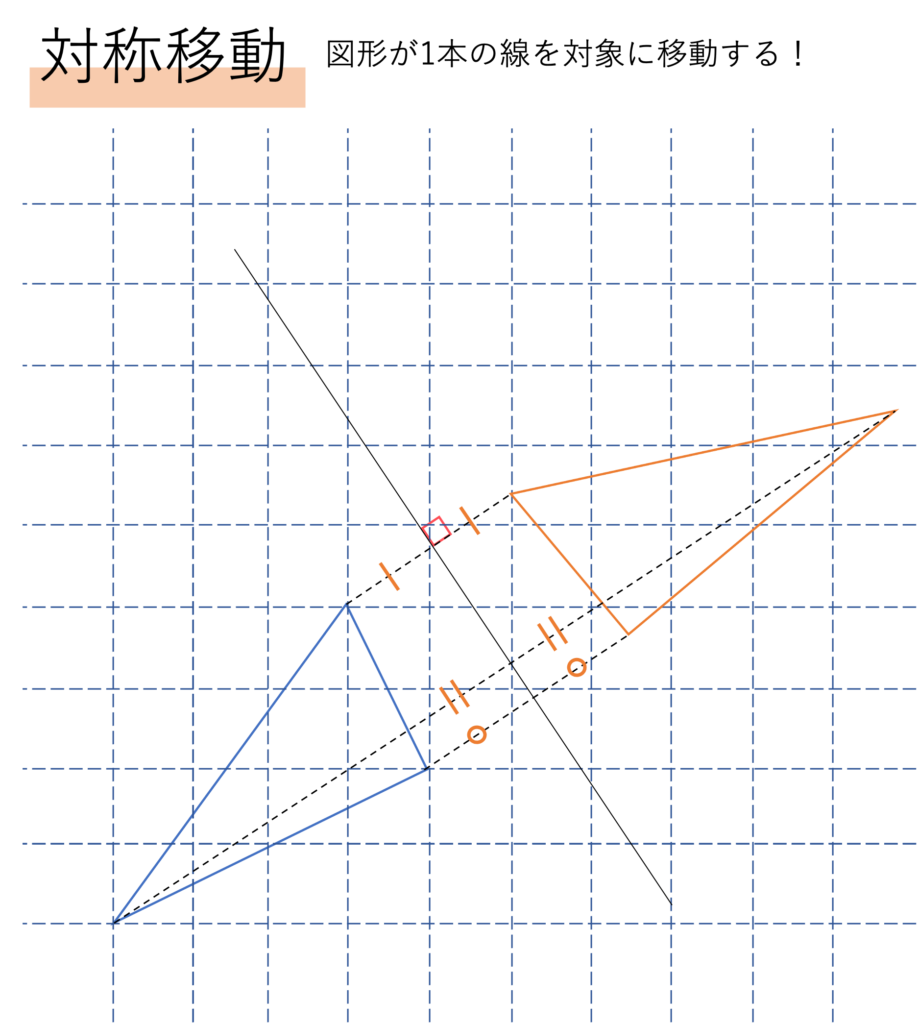
対称移動の場合,移動前後の点同士をつなぐと全ての線が平行になります。これだけだと平行移動と似ているようにも思えますが,対称移動で大きく重要となるのが対称の軸と呼ばれるものの存在です。この対称移動は1つの軸を基準として行われており,今回の図だと黒い線分がそれに当てはまります。上で確認した点を繋いだ線分はこの対称の軸と垂直に交わり,かつ点を結んだ線分を2等分します。そのため軸を探すときは点を結んで垂直かつ2等分になるポイントを押さえていくといいでしょう。
まとめ
- 移動とは図形や点が形を変えずに位置を変えること!
- 平行移動とは図形がスライドするように移動することを指し,移動の前後を結ぶと平行かつ等しい長さの線分が描ける!
- 回転移動では図形が向きを変えて移動することを指し,移動の前後を結ぶとある一点を中心とした弧が描ける!
- 対称移動では図形が鏡合わせのように移動することを指し,移動の前後を結ぶと平行な線分ができ,その線分を2等分して垂直に交わる対称の軸が浮かび上がる!
終わりに
今回の記事では図形や点の移動についてまとめていきました。本番の受験では,この要素を知っている前提の問題が登場します。そのため「移動とは何か」という部分が分かっていないと問題を解くことすらできません。したがって本記事でご紹介したことをしっかり覚えていただけますと幸いです。よろしければ下の参考書籍やおすすめ記事を使いながら,更なる学力向上に励んでいきましょう。


















