この記事は図形の折り返し問題に着目し,第1本目として基礎的な部分を解説していくものになっています。平面図形は中学受験で登場する算数の範囲の中でも難問が登場しやすい範囲の一つです。そのため幅広い形式の問題への理解を深めていくことが必要となります。それゆえ今回の記事を通して知識を広げていただけると幸いです。
Contents
図形の折り返しとは…?
まずは図形の折り返しとはどういう意味なのか・どういう問題なのか,ということについて説明していきます。図形の折り返し問題とは,長方形や正方形といった図形の一部を決まった線に沿って折り,そうして出来た新しい図形と元の図形との形を重ね合わせて考えていく問題のことを指します。具体的な問題のパターンや出題例については次の章で触れていきますが,文中に折る・折り返すといった言葉が入っていれば図形の折り返しと考えてしまっていいでしょう。求める対象は面積だったり角度の大きさだったりと様々ですが,折るという操作およびそこから見出せる特徴に基づいてこのような呼び方がされています。
この折るという操作は,大体の問題では1回のみ行われます。しかし複数回折り返しが行われたり,また1回の折り返しでも元々の図形が複雑だったり,折る際の線分が複雑だったりすると問題の難易度がグッと上がります。今回の問題では優しめの問題に着目しながら基礎的な攻略法をご紹介していきますので,読みながら・解きながら理解を深めていきましょう。
いくつかのパターンを見てみよう!
ここまでは図形の折り返しとはどういう問題かについてお話ししていきましたが,とはいっても実際の問題文や図がなければイメージがつきづらいかと思われます。そこでここでは図形の折り返し問題の例をいくつかご紹介させていただきます。
下の図は長方形を折ってできる図形です。アの角度の大きさを求めなさい。
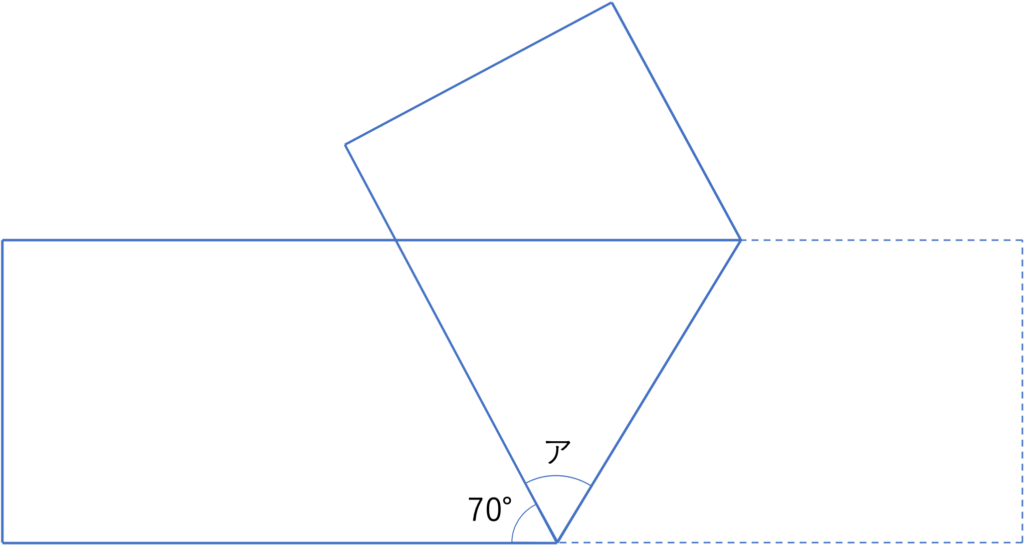
下の図のように正三角形の紙を折りました。紙が重なっている部分の面積は何cm2ですか。
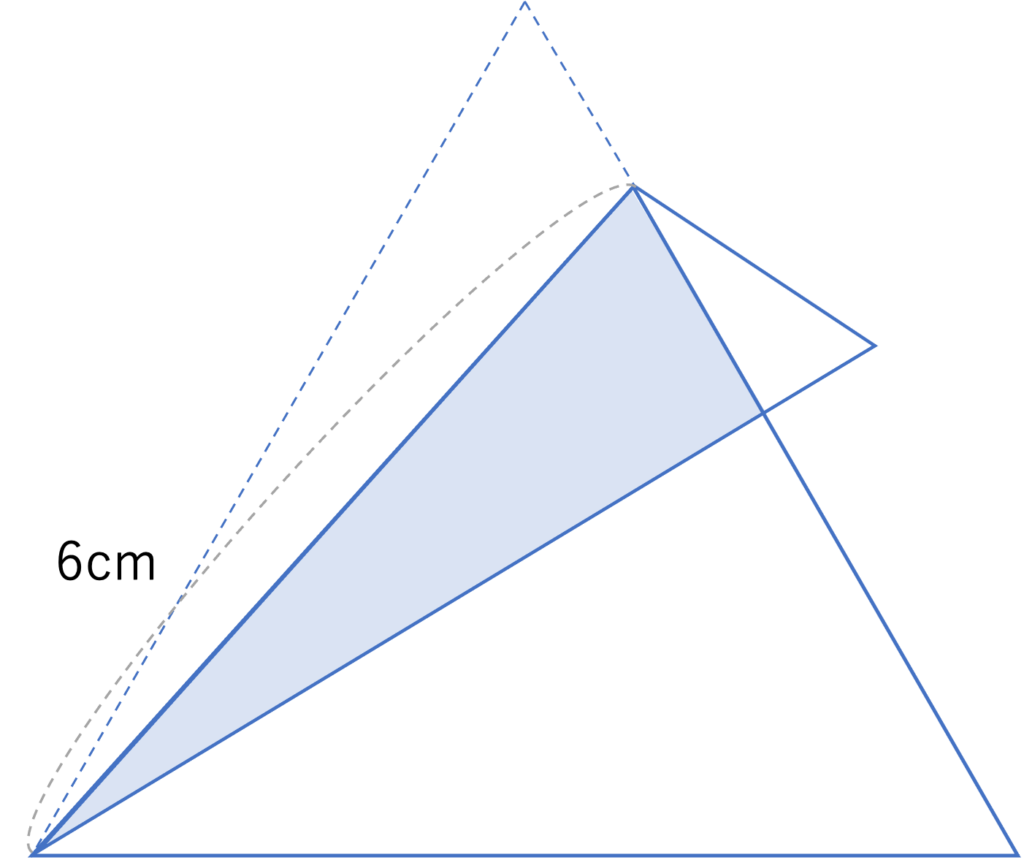
(早稲田中学校(2019),一部改題)
長方形ABCDの頂点Bが辺AD上にくるように折り返します。頂点Bが移る点がEで,Eは辺AB上にあり,CFが折り目であるとき,AFの長さを求めなさい。
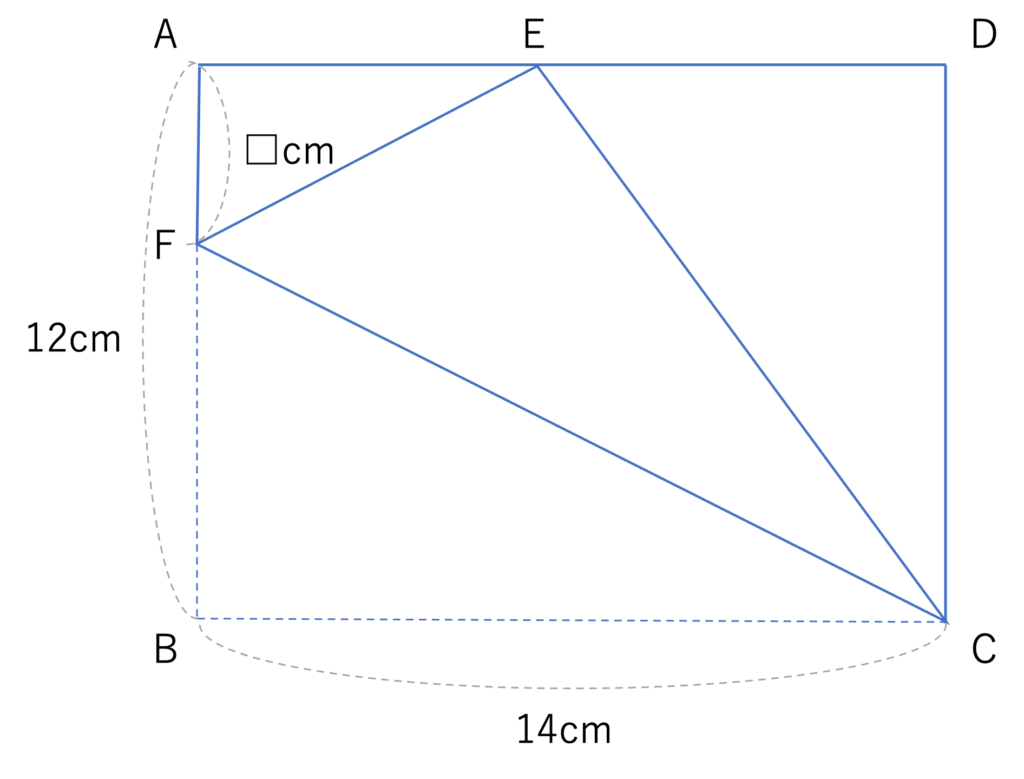
この3問だけでも様々な出題パターンがあることをご理解いただけたでしょうか。以上のように元になる図形も様々であれば,折り方も求めるものも多様なので,ベースとなる本質的な攻略法を頭に入れておくことが大切になることが分かりますね。まずは折り返し問題とはこのような複雑な平面図形の範囲の一部であるということ,そしてその問題文の大まかな構造や特徴を覚えておきましょう。
折り返し問題の解き方!
ここからは上でご紹介した1番目の問題を使いながら,図形の折り返し問題の攻略方法をお教えしていきます。まずは再度問題を掲載しておきますので,どうやって解けば答えがわかるのか・図形にどんな情報があるかを考えてみるといいでしょう。
下の図は長方形を折ってできる図形です。アの角度の大きさを求めなさい。

攻略法① 対応関係を把握しよう!
それではここからは攻略の手順をご紹介していきます。まずはどの文章題でも共通して重要となる問題文に書かれている内容の整理を行っていきましょう。特に図形の折り返しの問題ではどこからどこに向かって折ったのかという要素が問題を解く鍵になってきますので,図と文を見比べながら内容を眺めることは他の問題に増して重要です。今回の問題では長方形の右側を上向きにおり,そのときに70°の角度ができるという条件が提示されています。今回の操作は簡単だったとは言え,問題によってはより複雑な折り方も登場しますので,普段からまずは中身を整理することを意識していきましょう。
さて上の文で今回の問題では右部分から左上に向かって折ったと説明しましたが,この部分に問題を解く鍵があります。今回の問題は図形の折り返しですが,このとき折る前に存在していた部分の図形と折った後に新しく生まれた部分の図形は同じ形にならなければいけません。というのも,折り返し問題ではあくまで図形を折るだけなので,元の状態に戻せないといけないからです。今回の図形だと下のように2つの台形の部分が一致することになります。
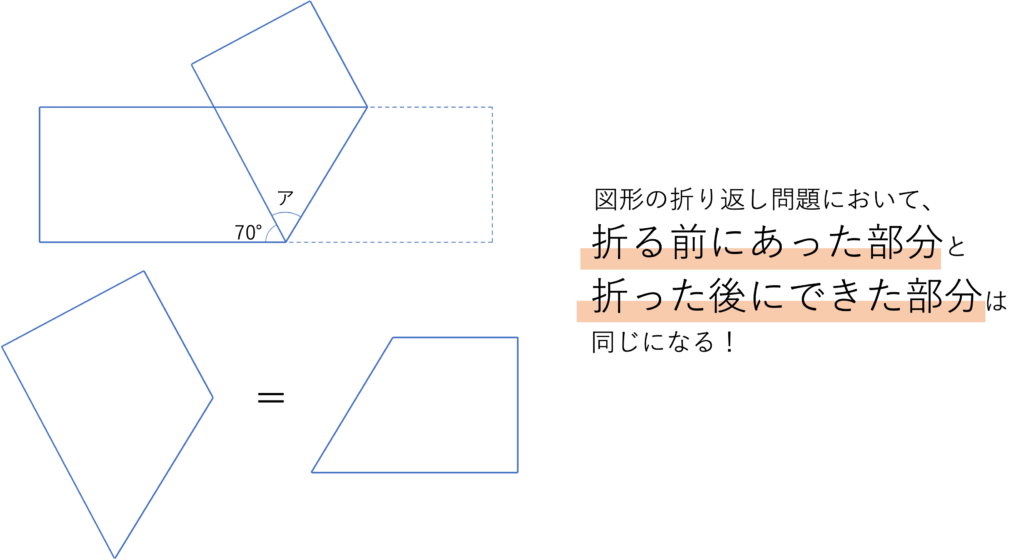
そして加えて注目しておきたいところが,当然のことですが,これらの同じ図形同士は折り線を境に正反対になっているということです。そのため以下でも詳しく見ていきますが,どの部分とどの部分が等しいのかを探るときは折れ線に着目するといいでしょう。
攻略法② 情報を埋めていこう!
さて1つ目のステップである同じ部分の図形の確認を終えたところで,続いては具体的な情報を埋めるというところに移っていきましょう。ここでの情報とはどこの角度とどこの角度が等しいとか,どこの線分とどこの線分が等しいとか,そういった図形に関する特徴のことを指します。今回の例題では,先ほど2つの台形が一致することを確認しましたが,そのことからいくつかの共通する要素が挙げられそうですね。このように折り返しをはじめとした移動によって位置が変わった図形・辺・頂点などのことを,元々の図形・辺・頂点に対応するといいます。つまり対応する辺であれば長さが,対応する角度ならその大きさが,対応する図形ならその形や面積が等しくなるわけです。このとき対応するもの同士には,○や×といった何らかのマークをつけておくことが多いです。今回の対応関係は下のようになります。なお直角の部分については一目瞭然なので省略します。
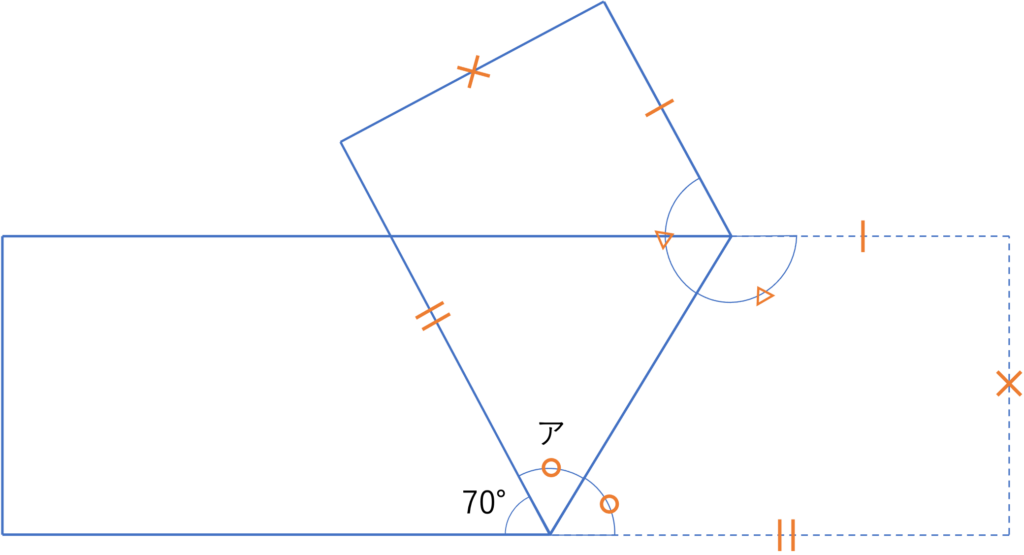
以上のように対応関係を図に落とし込んでいくことで,様々な情報が目で見て分かりやすくなります。簡単な問題でも書き込んでおく癖をつけておきましょう。今回の問題だとアの角と同じ大きさをする角が折れ線を挟んで反対側にも存在することが分かります。問題を解く上で重要な手がかりになりそうですね。
またマークの種類もいくつか頭に入れておくと,情報を整理していざ問題に挑戦するときや復習・見直しのため問題を見返したときに「この印はどういう意味だったっけ?」となりにくいためオススメです。
攻略法③ 整理した内容から計算を進めよう!
さて2つ目のステップでは折り返しという操作が関わってくるからこそ分かる対応関係に着目してきました。以降は上で導いた情報から計算を進めていきます。図形の折り返し問題はこれまで行ってきた一致・対応という関係に慣れるまでに時間がかかるので難しく感じてしまいやすいですが,情報の整理さえ済んでしまえば,後はくせのない平面図形の問題となんら変わりません。勉強した基礎を思い出しながら答えを求めていきましょう。
今回の問題だとアの大きさを求めましょう,という指示が出ていました。そのためアの存在する線分に注目していきましょう。いまこの線分上には3つの角度があり,うち1つは70°,うち1つはアになっていることが分かります。そのためアは180°-70°=110°よりは小さいと判断できますね。ここで先ほど確認した対応関係に着目すると,70°でもアでもない角度は図形を折って出来たものであることから,アと同じ大きさをしていることが分かります。そのためアの角度は180°から70°を引いた数を2で割った大きさになりますね。以上のことからアの大きさは(180°-70°)÷2=55°となります。
A.ア:55°
以上のように図形の折り返し問題では,対応関係さえ掴んでしまえば案外簡単に解くことができますので,他の文章題同様落ち着いて進めていきましょう。
まとめ
- 図形の折り返しとは図形の一部を決まった線に沿って折る問題のこと!
- 図形の折り返し問題は折る前に存在していた部分の図形と折った後に新しく生まれた部分の図形は同じ形になる!
- 一致する図形から辺・角・頂点の対応関係を掴もう!
- 対応関係さえ分かれば基本的な問題と同じ要領で解ける!落ち着いて計算しよう!
終わりに
今回の記事では図形への折り返し問題の解説の基礎編として,基本的な考え方や攻略法をご紹介していきました。冒頭で述べた通り,平面図形という範囲は難問が作られやすい分野ですので,早いうちから理解度を上げていきましょう。次回の応用編では受験問題を引用しながら実践的なテクニックをご紹介していきますので,下のおすすめ記事とあわせて参考にしてみてください。本記事が今後の学習のお役に立てば幸いです。


















