【大学受験物理】熱力学の基本的な解き方〜5つの手順に分けて解説〜

ここでは前回の「熱力学の基本的な考え方」に基づいて，実際に熱をどのように計算するのかを見る．

Contents

1 少しの復習
2 5つの手順
3 おすすめ記事
4 参考

少しの復習

前回のことを少し思い出そう．これからの熱力学の話で想定される系は以下の図1 であった．

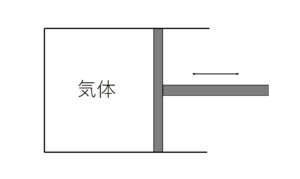
図1: 熱力学系

図1 の装置に対して「力学的な操作」を施し，気体の熱力学的な性質を探るのが基本的な考え方であった．

5つの手順

これから「熱」というものを求める手順を5 つに分けて述べるが，はじめにその手順をまとめておく．その手順は以下の通りである：

容器の大きさから気体の体積を，力のつり合いから気体の圧力を求める．
状態方程式から気体の温度を求める．
求めた温度から内部エネルギー変化を求める．
\(P-V\)図から気体のする仕事を求める．
熱力学第1 法則から気体に流入した熱を求める．

分からない言葉も含まれているだろうが，詳細はこれから述べる．

体積と圧力の決定

問題の設定から容器の体積を求めることができる．図1 の装置のピストンの底面積と容器の底面からピストンまでの距離から体積が分かる．

次に気体の圧力を求める．気体はピストンを押している．そしてピストンは外部からおさえられている．それらの力のつり合いから気体がピストンを押している力が求まり，それをピストンの面積で割ると圧力が求まる．

理想気体の状態方程式と温度の決定

さて，自分たちにできる力学的な操作は「圧力の測定」と「体積の測定」のみであることが分かった．ここからどうやって，熱だとか温度を知ることができるのか．結論を述べると，温度は理想気体の状態方程式から決まるのである．理想気体の状態方程式とは，

\(PV = nRT\)　(1)

のことで，\(P\)は圧力，\(V\)は気体の体積，\(n\)は気体のモル数，\(R\)は気体定数，\(T\)は絶対温度である．これは一連の実験の結果から得られたものであるが，実際はずれが生じる．つまりこの方程式が成立する気体のことを理想気体という．気体定数\(R\)は，

\(R = 8.31 J / mol K\)　(2)

という値を持つ．今，問題の設定上\(n\)は一定¹だから，\(nR\)は一定の値を持っている．したがって，\(P\)は圧力の測定から，\(V\)は気体の体積の測定から決まるので，状態方程式から温度も決まる．むしろ状態方程式は温度を定義するための式ということだ．だから入試問題において温度を求める問題では²，基本的には状態方程式を用いて求めることになる．

内部エネルギーの決定

次に内部エネルギーについて述べる．内部エネルギーも熱力学的な物理量であるが，入試で扱われる理想気体の場合，温度が決まれば内部エネルギーも決まってしまうので温度から計算することができる．具体的には内部エネルギー\(U\)は，

\(U = \frac{3}{2}nRT\)(単原子分子)

\(U = \frac{5}{2}nRT\)(二原子分子)　(3)

となることが知られている³ので，これを公式として覚えて計算すれば良い．内部エネルギーの変化も温度の変化が分かれば計算できる．

仕事

ここでは力学でも学習する仕事の復習と，熱力学での仕事の求め方について述べる．

ある物体を力\(F\)で，\(x_{1}\)の地点から，\(x_{2}\)の地点まで動かしたときの仕事は，以下の式で定義される⁴．

\(W = \int _{x_{1}}^{x_{2}}Fdx\)　(4)

いきなり積分が出てきて焦るかもしれないが，これは「(仕事) ＝（力）×（距離）」というものを，より正確に表現したものである．

積分の意味を思い出そう．この式の場合，ある力\(F\)で微小な距離\(dx\) だけ動かした仕事を，\(x_{1}\)の地点から\(x_{2}\)の地点まで積み上げたものである．なぜ積分で書くと正確なのかというと，一般に力\(F\)は\(x\)の関数で，場所によって異なる値を持つ．（図1 でピストンを押し込むことを想像してみよう．押すほど手応えが強くなるはずである．）したがって，積分でないと仕事を正確には表現できない⁵．

さて，この仕事は力学的な操作で求められる．力学的な操作で求まっているのは圧力と体積である．よって式(4) を圧力と体積で表現しよう．圧力\(P\)と力\(F\)の関係は，断面積\(S\)を用いて，

\(F = PS\)　(5)

と書ける⁶．これを式(4) に代入すると，

\(W = \int _{x_{1}}^{x_{2}}P(x)Sdx\)　(6)

となる．ここで，「（断面積）×（距離）＝（体積）」だから，

\(Sdx = dV\)　(7)

である⁷．よって仕事は，

\(W = \int _{V_{1}}^{V_{2}}P(V)dV\)　(8)

である．積分範囲が変わっていることに注意してほしい．この式から仕事が圧力と体積から求まることが分かる．ところで，積分は面積を求めるときにも使う．それと同じ考え方で，\(P-V\)図上での面積が仕事に相当する(図2 参照)．よって熱力学で仕事を求める場合は，\(P-V\)図を描いてその面積を計算することで求める．

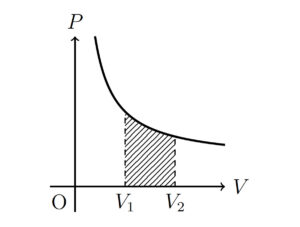図2: 仕事を表す面積

熱力学第1法則と熱の決定

さて最終的なゴールである熱の決定に入ろう．これも結論から述べると，熱は熱力学第1 法則から決まるのである．だからまずは，熱力学第1 法則の説明からしよう．

熱力学第1 法則とは，

\(\delta U = Q – W\)

であり，\(\delta U\)は内部エネルギー変化，\(Q\)は流入する熱，\(W\)は外にする仕事である．この熱力学的第1 法則はエネルギー保存則を表している．これは熱の定義式とも解釈できる．

これらの符号に注目してほしい．符号は以下の図3 のように定めている⁸．つまり，下線を引いたように気体に対して「入ってくる」ものを正，「出ていく」ものを負とした．参考書や問題集によって正負の定め方が異なる場合もあるので注意してほしい．内部エネルギーと仕事は，圧力と体積から求められることはすでに見たので，式(9) から熱を求めることができる．

以上が熱力学で熱を決定するまでの基本的な流れである．具体的な問題は次回以降の記事で紹介する．実際に計算をしながら今回の流れを定着させよう．

図3: 熱力学第1 法則のイメージ

¹容器への気体の流出入がない．

²問題の中には初めから温度が分かっているとして，圧力や体積を「逆算」させるものもある．

³マクロな視点における熱力学の枠組みからは得られない．

⁴簡単のため１次元で考える．

⁵力が一定の場合のみ，（力）×（距離）で仕事が求められる．

⁶圧力の定義は，「単位面積あたりの力」であったことを思い出そう．

⁷\(d\)の意味は「微小な」を表している．この式は，変数x から変数V への置換積分と考えても良い．

⁸この定め方は，熱力学がそもそも機械を動かすことから始まったことに由来している．つまり，ある機械中の気体を温めて，その結果外部に何かしらの仕事するというイメージに基づいている．

参考

花井遼介

こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。