| 前回：標本調査とデータの分類 | 次回：度数分布表とヒストグラム |
第３回 尾崎
前回の記事ではあらゆる測定データを量的データと質的データに分類した．今回はスタンレー・スティーブンスによって1946年に提唱された理論（Stevens, 1946）に基づき，測定尺度という観点から量的・質的データを全部で４つのクラスに分類する．データを適切に記述するという目的において，この理論を知っていることはたいへん有意義だと思う．なぜならば，測定尺度の異なるデータには，適用できる数学・統計学的操作（例えば，和や差に意味があるか・平均値をとることができるか）も異なるからだ．
なお，重要な話題ではあるものの，この内容はやや高校数学の範囲を超えている．読み飛ばしても先の記事の内容について大筋を理解する分には差し支えないよう配慮するので，気持ちを軽くして覗いてみてほしい．
Contents
測定尺度と水準
測定尺度
測定尺度とは物差しの目盛りのようなものである
統計学で扱うデータはみな，何らかの尺度（scale）によって測られている．測定における尺度（測定尺度，scale of measurement）とは，対象に値を割り当てるルールのことだ．
たとえばサンマの長さを測りたいとしよう．そのためには，物差しの端をサンマの口の先に当てて尾の部分の目盛りを読み取ればよい注１．このとき得られる値は，目盛りの単位（ミリメートル，またはインチだろう）に応じたものになる．つまり，物差しに記されている目盛りに従って，測定対象のサンマに実数値が割り当てられている．この例では目盛りが測定の尺度に相当すると考えることができる注２．
データに対して行うことが可能な数学・統計学的操作は測定尺度に依存する
さて様々な測定尺度に対応する目盛りを図１に示した．皆さんが上記の例で想像した物差しは，この中で言うといずれに近いだろうか？
普段使っている文房具の物差しは（c）または（d）のような見た目をしていると思う．しかし，物差しの端をサンマの口先に当てて測るのであれば，（d）がこの中で最も適切な目盛りであるといえるだろう．
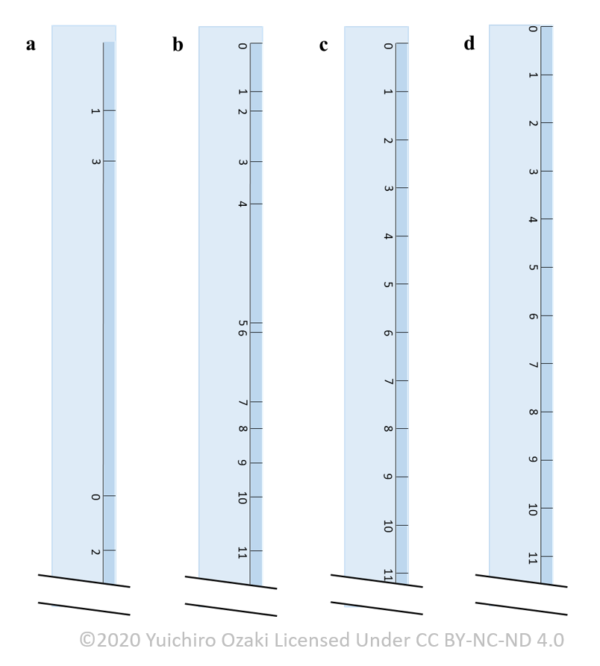
図１ ４つの尺度の概念図．それぞれの「物差し」の目盛りは異なる水準の尺度を表現している：（a）名義尺度，（b）順序尺度，（c）間隔尺度，および（d）比率尺度．
仮に物差し（c）をサンマに当ててみたとき，目盛りが示す値は真の体長にいくらかの定数値が加えられたものとなる．したがって，物差し（d）のように比をとって「個体Aが個体Bよりも何倍大きい」ということを調べることはできない．しかし「個体Aが個体Bよりも何cm大きい」などと差をとることには意味がある．
また物差し（b）を用いた場合，目盛りの間隔がバラバラなので差をとって「個体Aが個体Bよりも何cm大きい」といったことを調べることもできないが，「個体Aが個体Bよりも大きい（小さい）」のように大小の比較はできるだろう．
物差し（a）は上手い使い方が思いつかない（笑）．しかし，世界の海にはサンマの仲間が数種類いるので，ひょっとしたら種を判別するのに使えるかもしれない注３．つまり物差し（a）の目盛りの値によって「個体Aが個体Bよりも大きい（小さい）」かを調べることはできないが，「個体Aと個体Bは種類が同じである（異なる）」といった等しさの判定は可能である．
こうした例から，物差しで測られた値に対して行うことができる数学的な操作は測定尺度（目盛り）に依存して異なるということが判る．統計学でデータに対して行うあらゆる操作（例えば，平均値をとる，最大・最小値を調べるなど）は，数学的な操作に基づいている．したがって，データに対して適用できる統計学的操作もまた測定尺度に依存する．
注１．実際に魚の長さを測定しようとすると，どこからどこまでを測ればよいのかきっと悩むことになるだろう．実はサンマの場合は，魚類の中でも体長の測り方が少し特殊で，下あごの口先（下顎の吻端）から尾鰭にある肉質部の後端までを測ることが多い．この部分の長さを魚類の研究者たちは肉体長（knob length）と呼ぶ．
注２．変数に値を割り当てる規則（rule）である尺度（scale）を，物差し（ruler）の表面に描かれている目盛り（scale）として説明した．我ながらなかなか精確な例えで表現できたものだとドヤ顔しているのだが．．．（笑）
注３．おそらくは困難である．
測定尺度の水準
測定尺度には水準の高い・低いがあり，高い水準のデータほど適用できる統計学的操作が多い
割り当てられた値たちが持つ数学的構造によって尺度の水準（level）が異なるとされる．
たとえば，図１の物差し（d）によって得られた値は，比をとること，差をとること，大小の比較，そして等しさの判定のすべてが可能である．一方，物差し（c）では比をとることができず，差をとることと大小の比較，等しさの判定だけが可能である．したがって，物差し（d）の測定尺度は（c）の測定尺度よりも「水準が高い」と表現される．
図１において測定尺度の水準は低いものから順に（a），（b），（c），（d）であり，それぞれ名義尺度（nominal scale），順序尺度（ordinal scale），間隔尺度（interval scale），比率尺度（比例尺度，ratio scale）という．水準が高位の測定尺度は低位の測定尺度の特別な場合であり，自分より低位の測定尺度が持つ数学的構造をすべて備えている．
測定尺度の観点から，変数およびデータを４つのクラスに分類することができる（表１）．
表１ 尺度水準に基づくデータの分類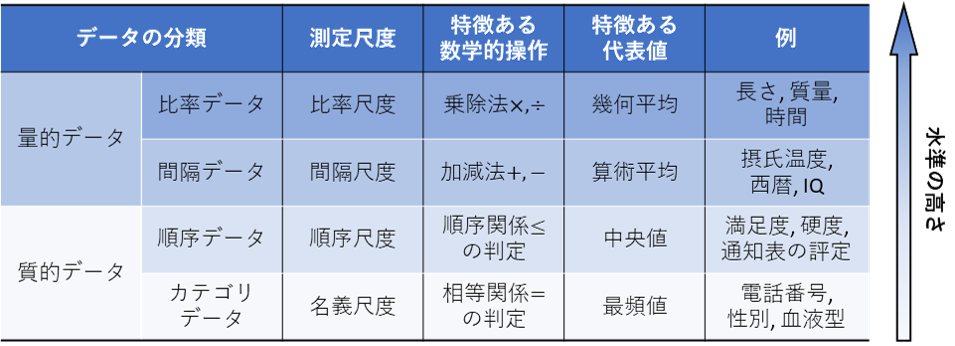
＊本表はStevens（1946）および栗原（2011）を基に作成した．
高い水準の尺度であるほど，変数やデータから算出することができる数値（統計量）の種類は多くなる．表１の各行に示す測定尺度は，自分よりも低水準の測定尺度で許されるすべての数学的操作と代表値を用いることができる．
たとえば，間隔尺度は加減法（足し算と引き算）と順序関係（大小の比較），相等関係（等しさの判定）のすべてを備えているが，乗除法（掛け算と割り算）を行うことは適切でない．また間隔データに対して算術平均や中央値，最頻値を求めることはできるが，幾何平均を求めることは妥当でない注４．
注４．最頻値，中央値，平均値（算術平均や幾何平均）は，いずれもデータの「真ん中」を表すために算出される統計量（代表値）である．本連載の後の記事で詳しく説明する．
測定尺度に基づくデータの分類
上記４つの尺度で測られたデータについて，それぞれを水準が低いものから順に紹介しよう．
名義尺度／カテゴリデータ
名義尺度で測られたカテゴリデータは分類のラベルを表す
名義尺度（nominal scale）は単に分類を行うためのラベルとして数値を個体に割り当てる．名義尺度で測定されたデータをカテゴリデータ（カテゴリカルデータ，categorical data）という．
生徒の郵便番号のデータはカテゴリデータである．それぞれの郵便番号が住所の分類を表すラベルとなっている．また性別 {男性, 女性, $\cdots$} や血液型$\{\rm{O, \, A, \, B, \, AB}\}$のように，数字以外の文字で表される要素がラベルを表す値であってもよい．こうした場合もO型を0，A型を1，B型を2，AB型を3というように数値にコード化することができるので本質は変わらない．
名義尺度の変数が「分類」というより，「個体そのもの」のラベルとなっている場合もある．たとえば生徒の電話番号のデータは，それぞれの番号が（兄弟姉妹がいない限りは）ただ１人の生徒と対応している．このようなときも，個体のレベルに至るまで詳細に分類を行った特別な場合と考えることで，他と同じく分類を表すカテゴリデータとみなすことができる．各市町村から住民に指定される個人番号（通称，マイナンバー）もこうした「個体レベルの分類」を表すカテゴリデータの１つだ．
名義尺度で測られた変数の値どうしでは，どちらがより大きいかといった順序の判定や加減法，乗除法などは一般に行うことができない．等しい（同じ分類に属す）か，そうでない（同じ分類に属さない）か，といった相等性の判定だけを行うことが可能だ．
したがって，データの中に同じ値がいくつ含まれているのか（度数，degree）を数えることは妥当な操作である．統計学ではカテゴリデータの代表値注４として，度数カウントによって求められる最頻値を使う．中央値や平均値などは，相等性の判定よりも高い水準の数学的操作を前提とするので，カテゴリデータの代表値には一般に用いることができない．
またデータの中心からの「距離」を考えることができないため，標準偏差などをカテゴリデータのばらつきを表す指標として計算することには意味がない．
順序尺度／順序データ
順序尺度の測定値どうしには大小関係がある
– 順序尺度
間隔尺度／間隔データ
間隔尺度の測定値どうしの差には意味がある
– 間隔尺度
比率尺度／比率データ
比率尺度の測定値どうしの比には意味がある
– 比率尺度
注．カテゴリデータという語は，順序尺度以下の水準で測定されたデータを表す語（つまり，本稿でいう質的データと同義）として用いられることもある．
用語のおさらい
練習問題
問題１ 次の各変数について尺度水準を答えよ．
（１）野球選手の背番号
（２）川の流れの速さ
（３）テストの得点
（４）牛肉の肉質等級（$\{1, \, 2, \, 3, \, 4, \, 5\}$の五段階評価）
（５）日付（※日数ではない）
（６）メダカの個体数
（７）ヒトの性別コード（ {0 : 性別不明, 1 : 男性, 2 : 女性, 9 : 性別を適用できない} の区分）注５
（８）学校の期末テストの総合得点
解答案
問題１
（１）名義尺度，（２）比率尺度，（３）間隔尺度，（４）順序尺度
（５）間隔尺度，（６）比率尺度，（７）名義尺度，（８）順序尺度
注５．ISO 5218という，ヒトの性別表記についての国際規格である．国際標準化機構（ISO: International Organization for Standardization）によって提案されている．割り当てられた数値の大小にはいかなる差別的な意味も含まれていないとされる．
