【高校１年生～大学生】「データの分析」を基礎から徹底解説！

第２回　尾崎

　統計的なデータとは，そもそもどのようなもののことをいうのだろうか？データの整理方法についてあれこれと紹介を始める前に，データが得られるまでの枠組みやデータの種類による特性の違いについて，ざっと説明しておこう．

　「データの分析」を初めて学ぶ方は，目次の【発展】や【補足】と付された事項を読みとばし，第４回の記事へ進んでいただいても構わない．データの扱いに慣れてきた頃，本記事をもう一度読み返していただけると効果的に学習のお手伝いができるのではないかと期待する．

Contents

1 データを得るまでの枠組み
- 1.1 標本調査
- 1.2 用語のおさらい
2 データの分類
3 まとめ
4 おすすめ記事
5 参考文献

データを得るまでの枠組み

　まずは統計学において欠かせない標本調査（sample survey）というアイディアについて簡単に紹介する．実際に自分自身でデータを分析しようとする際や，統計的推測まで学ぶとき特に重要になるので，「そんな話もあったな」と頭の片隅に置いていただけるとよいだろう．

標本調査

標本調査では，母集団の部分集合である標本について性質を調べる

　ある池に生息するメダカを調査したいとしよう（図１）.

　このとき興味の対象である，池にすむすべてのメダカの集まりが母集団（population）である^注１. 母集団に属すメダカ一匹いっぴきのことを個体（individual）という．

　池にすむ個体すべてを根こそぎ捕まえて調べるのはあまりに大変なので, 一部の個体を網で捕まえて調べることにする．採集された測定対象となるメダカたちの集合は標本（sample）という^注２．またこのように興味の対象である母集団の部分集合を取り出して行う調査のことを標本調査（sample survey）という．標本として100匹のメダカを捕まえた場合，標本の大きさ（sample size）というのはこの100という個体数のことを指す^注３．

　さて「ある時点でこの池にすむメダカ」を母集団とする場合は，たとえ数が多くとも個体数に限りがある．このように，有限個の個体から成る母集団のことを有限母集団（finite population）と呼ぶ．

　一方，無限個の個体が属す集合を調査対象にすることもできる．たとえば，池にすむメダカが実は新種であるなどの理由で，この池を産地とするメダカそのものが持つ性質を知りたいとする．そうした場合には，調査対象となる母集団として有限な個体の集まりを想定することができないだろう．個体の数が有限でない母集団を無限母集団（infinite population）という．

標本をある変数について（測定して）得られる値たちのことをデータという

　標本として捕まえたメダカたちを調べよう．

　決められた一定の手順でメダカを観測・計測して，体長，体重，性別などの値を割り当てることを測定（measurement）という．測定の対象となる性質は変数（variable）^注４，５，そして実際に測定して得られた値たちはデータ（data）である^注６．

　メダカたちの体長を変数として測定する場合は，

$\begin{equation}
22.8, \quad 21.9, \quad 24.5, \quad 21.7, \quad 21.9, \quad 23.1, \quad 23.0, \quad 22.1, \quad 23.3, \cdots \, (\rm{mm})
\end{equation}
$

といった値がデータとして得られるだろう.

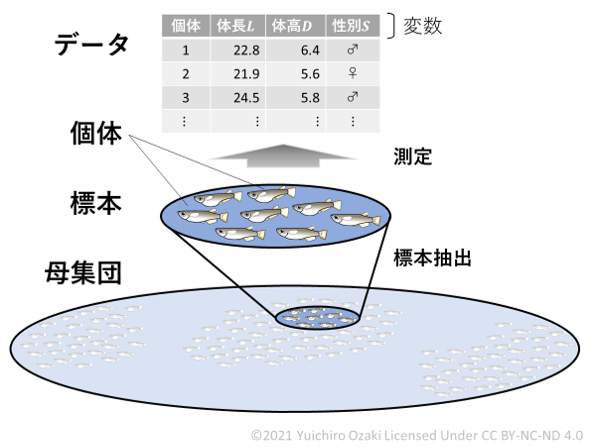
図１　ある池にすむメダカたちを母集団とした標本調査

注１．母集団という用語の英訳には，実はpopulationとuniverseの２語がある．意味にも違いがあり，経済系の統計学など，分野によってはこれらを使い分けているらしい．本稿のニュアンスだと厳密にはuniverseの方を用いるべきとも考えられるのだが，いくつかの理由によりここではpopulationを採用した．

注２．母集団と標本の区別は記述統計学においてはしばしば曖昧となる．より下流の解析において統計的推測などを行う際はこれらの概念が非常に重要である．なお母集団に属すすべての要素を標本とする調査を全数調査と呼ぶ．全数調査は，標本調査において母集団と標本が等しい特別な場合だと考えることができる．

注３．標本の大きさ (sample size) と似ているが意味の異なる用語に標本数 (sample number) がある．注意が必要だ．標本数とは調査によって得られた集団の数を指す．100匹のメダカを捕まえる標本調査を毎年一度，20年間にわたって行ったとする．このとき標本が全部で20集団あるので標本数は20ということになる．他方，１つひとつの標本の大きさは100である．

注４．変量（variate）という用語もある．変数（variable）と厳密には意味が異なるが，面倒くさいので誤解が起きる心配がないときには，あえて区別せずに用いる．

注５．【発展】確率論を統計学に適用する数理統計学（mathematical statistics）という分野では，変数と測定を同一視する．変数を考えるというのは，母集団から標本を取り出して，体長や体重，性別などの特性を測定することに相当するためだ．つまり，個体$\omega\in\mathit{\Omega}$を変数$X$について測るというのを数学的に捉えると，$\omega$に対して値$X(\omega) \in S$を割り当てるという写像を考えていることになる： $X:\mathit{\Omega} \to S; \quad \omega \mapsto X(\omega).$

注６．データ（data, 単数形はdatum）という語は事実や資料，数値などを指す語として，分野や文脈に依存してやや異なる意味で用いられている．本稿では，用語を整理して見通し良く学ぶ目的で，（統計的な）データを「標本をある変数について（測定して）得られる値の組」という意味として使うことにした．【以下，発展】なおデータに基づいて一定のルールで計算された値のこともデータと呼ぶことができる．明確に表現すると，データ$\mathcal{D}=(x_i)_{i \in I}$を関数$f$で写した$f(\mathcal{D})$もまたデータと呼ぶということだ．変数$X$を$f$で写すというプロセスを測定の段階に込めて解釈し，新たな変数$f(X)$を考えているものとみなせばよい．

用語のおさらい

　用語がたくさん出てきたので，重要なものを整理しておこう．

母集団（population）：ある調査・実験において観測や測定の対象となるもの全体からなる集合．
- 有限母集団（finite population）：有限個の要素からなる母集団．
- 無限母集団（infinite population）：無限個の要素からなる母集団．
個体（individual）：母集団に属す各要素．
標本（sample）：調査対象となる，母集団の部分集合．
標本調査（sample survey）：母集団のうち一部の個体を抽出して得られた標本に対して行う調査．
標本の大きさ（sample size）：標本に含まれる個体の数．
変数（variable）：観測や測定の対象となる性質．あるいは個体に測定値を対応付けるもの．
データ（data）：標本をある変数について測定することで得られた値の組．

データの分類

様々な視点に基づいてデータを分類することができる

　実際に何かしらの調査やデータ分析を行ってみると，一口にデータといっても色々な性質のものがあることに気づく．データ（あるいは変数）を分類するためのいくつかの方法を紹介しておこう．データの種類に応じて解釈や分析の方法が変わってくるので，どのような視点に基づいて分類できるのか理解することはきわめて重要だ．

データの次元

　さまざまなデータの分類法のうち，まずは次元（dimension）という観点について紹介する．

d次元データ

各個体についてd個の変数を測定して得られるデータをd次元データという

　先の章では池で捕まえたメダカの体長を測定するという例を挙げた．このように標本の各個体につき１つの変数を測定して得られるデータを１次元データ（1-dimensional data）という．大きさ$n$の標本から得られる１次元データは，一般に添え字を使って次のように表すことができる：

$\begin{equation}
x_1, \, x_2, \, x_3, \, \cdots , \, x_n.
\end{equation}
$

　各個体について体長だけでなく体高も測るというように２つの変数を測定することも頻繁にあるだろう．こうして得られる２次元データ（2-dimensional data）は，一般に

$\begin{equation}
(x_1, \, y_1 ), \, (x_2, \, y_2 ), \, (x_3, \, y_3 ), \, \cdots , \, (x_n, \, y_n )
\end{equation}
$

のように書くことができる．

　任意の自然数$d$に対して，d次元データも同様に定義される．$i$番目の個体（$i = 1, \, 2, \, 3, \, \cdots , \, n$）の$d$次元データは，

$\begin{equation}
(x_{i1}, \, x_{i2}, \, x_{i3}, \, \cdots , \, x_{id})
\end{equation}
$

のように表せる．

【補足】多次元のデータの記法

d次元のデータを数列やベクトルとして表現することがある

　さて表記を簡単にするためのtipsとして少し先取りした内容にも言及しておこう．

　もし数学Bをすでに学んでいれば，

$\begin{equation}
2, \quad 4, \quad 6, \quad 8, \quad 10, \quad 12, \quad 14, \quad 16
\end{equation}
$

のように数が並んだもののことを数列（numerical sequence）と呼ぶことをご存知かもしれない．有限個の数が並んでいるときは，この数列を

$\begin{equation}
(2, \, 4, \, 6, \, 8, \, 10, \, 12, \, 14, \, 16)
\end{equation}
$

といった要領で，かっこ$( \, )$で囲んで表記する．数列の要素を左端から順に，第1項，第2項，第3項，…，第8項と呼ぶとき，この数列の第$k$項（$k=1, \, 2, \, 3, \, \cdots , \, 8$）は$2k$と表すことができる．そこで式(6)を

$\begin{equation}
(2k)_{k=1}^8
\end{equation}
$

のように端的に表現する^注７．
　先ほど$d$次元のデータを式(4)のように表したが，これはまさに数列の記法である．d次元データは数列として解釈することができるのだ．したがって，$d$次元データを式(7)のように，

$\begin{equation}
(x_{ik})_{k=1}^d
\end{equation}
$

と書くことが可能だ．
　式(8)の記法によって，次元$d$や添え字$k$の取りうる値を明示しつつ任意の次元のデータが簡潔に表現できる．

　また数学Bをすでに学ばれている方は，いくつかの「数」を並べた組がベクトル（vector）であることを知っているだろう^注８．そのようなベクトルは数列の特別な場合であり，２つの数$a, \, b$を並べて書いた数列$(a, \, b)$を２次元ベクトルという．１文字で表したいときはベクトルであることが判るように

$\begin{equation}
\overrightarrow{v} = (a, \, b)
\end{equation}
$

などと，文字の上に矢印を付けて表記する．名前の付け方は$\overrightarrow{x}$でも$\overrightarrow{p}$でも，混同の恐れがなければ$\overrightarrow{a}$や$\overrightarrow{b}$でもよい．

　上記の理由から，「数」を値に持つd次元データはベクトルとしても表現できる．$i = 1, \, 2, \, 3, \, \cdots , \, n$について

$\begin{equation}
\overrightarrow{x_i} = (x_i, \, y_i)
\end{equation}
$

のように表すことにすれば，式(3)に示した２次元データは

$\begin{equation}
\overrightarrow{x_1}, \, \overrightarrow{x_2}, \, \overrightarrow{x_3}, \, \cdots , \, \overrightarrow{x_n}
\end{equation}
$

と書ける．

　３つの数$a, \, b, \, c$を$(a, \, b, \, c)$のように並べて書いたものを３次元ベクトルという．同様に，$d$個の数を並べた$(a_1, \, a_2, \, a_3, \, \cdots \, a_d)$のことを$d$次元ベクトルと呼ぶことは想像に難くない．

　さて$i = 1, \, 2, \, 3, \, \cdots , \, n$について

$\begin{equation}
\overrightarrow{x_i} = (x_{i1}, \, x_{i2}, \, x_{i3}, \, \cdots , \, x_{id})
\end{equation}
$

とすれば，$d$次元データを

$\begin{equation}
\overrightarrow{x_1}, \, \overrightarrow{x_2}, \, \overrightarrow{x_3}, \, \cdots , \, \overrightarrow{x_n}
\end{equation}
$

のように簡潔に書くことができる．しかもこれは，式(11)と全く同じ見た目をしている．つまり，データの次元によらず一般に使うことができる記法だ．

注７．伝統的な記法では式(7)を$\{ 2k \}_{k=1}^8$のように表記する．日本の高校で使われている，多くの数学の教科書もこの伝統的な書き方に従っているから，式(7)のようにかっこ$( \, )$を用いた記法を見慣れないと感じた方もいるかもしれない．現代の数学では波かっこ$\{ \, \}$を，主に集合（set）を表すために用いる．集合は要素の順番や重複を考慮しないので，$\{ 2, \, 4, \, 6, \, 8 \}$や$\{8, \, 6, \, 4, \,2 \}$，$\{ 2, \, 2, \, 4, \, 6, \, 8\}$がすべて同じであるとみなされる：$\{ 2, \, 4, \, 6, \, 8 \} = \{8, \, 6, \, 4, \,2 \} = \{ 2, \, 2, \, 4, \, 6, \, 8\}. $ 一方，要素の順番や重複を考慮するようなものの集まりは列（sequence）と呼ばれ，集合と区別するためにかっこ$( \, )$を用いて表記する．列においては$(2, \, 4, \, 6, \, 8) \neq (8, \, 6, \, 4, \, 2) \neq (2, \, 2, \, 4, \, 6, \, 8)$である．

注８．【発展】ここでいう「数」とは，厳密には体（field）と呼ばれるもののことを指している．我々がふだん「数」と言ったとき暗黙に想定する複素数や実数などは体であるから，あまり身構えなくても大丈夫だ．そうした「数」を並べたものは自然にベクトルとみなすことができ，特に数ベクトル（numerical vector）と呼ばれる．詳しくは線形代数学の教科書や記事（近日公開予定）を参照してみてほしい．

【補足】時系列データ

時系列データは変数の順序に意味がある特別な多次元データだ

　時間の経過に従って測定されたデータを時系列データ（time series data）という．１時間ごとの株価や，1日おきに測ったメダカの体長などは時系列データの例である．

　時系列データは時刻$t=1, \, 2, \, 3, \, \cdots , \, T$における測定値の組であり，$(x_1 , \, x_2 , \, x_3 , \, \cdots , \, x_T)$あるいは$(x_t)_{t=1}^T$のように表すことができる．$T$個の変数について測定して得られるのだから，T次元データである．

　時系列データがふつうの多次元データと異なる最大の特徴は，変数の順番に意味があるということだ．時系列データでは変数が時刻$t=1, \, 2, \, 3, \, \cdots , \, T$の順に並んでいることが重要であり，もし時刻間で変数を入れ替えてしまうと情報が著しく損なわれる．

　ふつうの多次元データに対して行うほとんどの解析方法は変数の順番を考慮していないから，時系列データを扱う際には可視化・定量化のいずれにおいても特別な方法を用いる必要がある．

　時系列データの具体的な解析方法については後の記事で紹介する．

【発展】離散型と連続型

　続いては離散型と連続型という視点について紹介しよう．推測統計学において，変数が従う確率分布を考察するときにこれらの型の違いがとても重要となる．

　この内容はやや高校数学の範囲を超えている．読み飛ばしても先の内容について大筋を理解する分には差し支えない．

とびとびの値しか取り得ないデータを離散型，連続値を取り得るデータを連続型という

　メダカ8匹がある日に産んだ卵の個数：

$\begin{equation}
17, \quad 0, \quad 8, \quad 0, \quad 11, \quad 21, \quad 15, \quad 9
\end{equation}
$

などのように, とびとびの値しかとりえない量を表すデータ（あるいは変数）のことを離散型（discrete type）という．個数や回数などといったカウントできる量のデータは離散型である．

　一方，メダカの体長や体重，卵がかえるまでの時間，泳ぐ速度などのように連続値をとりうる量を表すデータ（あるいは変数）のことを連続型（continuous type）という．

　なお連続値をとりうる変数であっても，測定を行う際の精度が有限であるために，厳密に考えるとデータの値はほとんどの場合で離散的な値しかとりえない．しかし，そうした場合でもデータを連続型とみなして解析を行うことが多い．

【発展】量的データと質的データ

　続いては統計学で扱うあらゆるデータを，量的データと質的データという２つの種類に分けてみよう．なお次回の記事では測定尺度というアイディアに基づいて，量的データと質的データをさらに詳しく分類する予定である．

　この内容はやや高校数学の範囲を超えている．読み飛ばしても先の内容について大筋を理解する分には差し支えない．

量的データは数量を表し，和と差が意味を持つ

　メダカたちの体長や池の水温などのように数値によって何らかの量を表しているデータのことを量的データ（quantitative data）という．また数量を表す変数のことは量的変数という．

　先の2.2節では，とびとびの数値だけをとる離散型データと途切れのない数値をとりうる連続型データという分類について紹介した．離散型のデータと連続型のデータはいずれも量的データである．

　量的データは数量を表しているので，値どうしでの和や差をとることに意味がある．

質的データは区分を表し，和と差が必ずしも意味を持たない

　一方，生徒の血液型を$\{\rm{O, \, A, \, B, \, AB}\}$の４タイプで表すデータや，サービスへの満足度を５段階 {5 : 満足, 4 : やや満足, 3 : 普通, 2 : やや不満, 1 :不満} で表すデータのように，数量ではなく区分を表すデータのことを質的データ（qualitative data）という．区分を表す値をとる変数は質的変数である．

　質的データであってもそれぞれの区分に数を割り当てることで，数値によって表現することは可能である．たとえば生徒の血液型データ：

$\begin{equation}
\rm{A, \quad O, \quad A, \quad B, \quad AB, \quad A, \quad B, \quad O, \quad \cdots}
\end{equation}
$

は，O型，A型，B型，AB型を0，1，2，3として表すことにすれば，

$\begin{equation}
1, \quad 0, \quad 1, \quad 2, \quad 3, \quad 1, \quad 2, \quad 0, \quad \cdots
\end{equation}
$

とコードできる．

　このように質的データは数値で表されることもあるのだが，その和あるいは差に必ずしも意味がないという点で量的データと異なっている．たとえば血液型データにおいて，AB型（コードは3）とA型（コードは1）で和をとると$3+1=4$となるが，この値を解釈することは困難だ．

　また男性と女性，既婚と未婚などのように変数の値が２通りしかとりえない質的データのことを特に２値データ（binary data）という．2値データの場合は男性を0, 女性を1というように$\{ 0, \, 1 \}$でコードすることが多い^注９，10．このとき，ある10人の実験参加者の性別データ：

$\begin{equation}
1, \quad 0, \quad 0, \quad 1, \quad 1, \quad 0, \quad 0, \quad 1, \quad 0, \quad 0
\end{equation}
$

において，データ全体で和をとった4という値は女性の人数を表している．$\{ 0, \, 1 \}$上の要素を値にとる２値データの場合は，質的データであっても和に意味を見出せるということに注意しよう．

注９．男性を1，女性を0のように値を割り当てても全く差し支えない．数値の大小には，いかなる差別的な意図も含んでいない．

注10．$\{ 0, \, 1 \}$上の要素を値にとる２値変数のことをダミー変数（dummy variable）という．ダミー変数は和をとるなど，普通の質的変数よりも高い水準の数学的操作を行うことができる．統計解析を行うときの多くの場合において，質的データは量的データよりも適用できる解析手法が限られている．しかし，このダミー変数の性質を活かすことで，しばしば質的データに対しても量的データのための解析手法を利用することができる．

用語のおさらい

　新たにたくさんの用語が登場したから，重要なものを簡単にまとめておこう：

データの次元
- １次元データ（1-dimensional data）：各個体について１つの変数を測定して得られるデータ．
- ２次元データ（2-dimensional data）：各個体について２つの変数を測定して得られるデータ．
- ｄ次元データ（$d$-dimensional data）：各個体について$d$個の変数を測定して得られるデータ．
離散型と連続型
- 離散型（discrete type）：とびとびの値しかとりえない量的データ（あるいは量的変数）
- 連続型（continuous type）：連続値をとりえる量的データ（あるいは量的変数）
量的データと質的データ
- 量的データ（quantitative data）：数量を表し，和や差に意味があるデータ．
- 質的データ（qualitative data）：区分を表し，和や差に必ずしも意味がないデータ．

練習問題

問題１　次のデータは何次元データであるか？
（１）全校生徒の身長，座高，体重のデータ（各生徒が個体）
（２）英語の文書にアルファベット$\{ \rm{a, \, b, \, c, \, \cdots , \, z} \}$が何文字ずつ含まれているかを調べたデータ（各文書が個体）

問題２　次の変数は離散型か，それとも連続型か？
（１）あなたの毎朝の体温
（２）あなたが通う学校へ，1日に登校した生徒の人数
（３）あなたの1日のくしゃみの回数
（４）あなたの飼っているイヌが1日に歩行した距離

問題３　次のデータは量的データか，それとも質的データか？
（１）問題２の（１）から（４）のデータ
（２）顧客の電話番号データ
（３）企業の株価データ
（４）全校生徒の通知表の評定データ（５段階で評価する）

解答案

問題１　（１）３次元データ，（２）26次元データ

問題２　（１）連続型，（２）離散型，（３）離散型，（４）連続型

問題３　（１）量的データ，（２）質的データ，（３）量的データ，（４）質的データ

まとめ

　今回の記事では，これから記述統計学で扱っていくデータがどのようなものなのかを明確にしておくため，データが得られるまでの枠組みやデータの分類方法について概説した．ポイントは以下の通りだ：

統計的なデータは標本調査によって得られる．
データを様々な方法で分類することができ，データの種類によって解析の方法が異なる．
- d個の変数を測定して得られるデータをd次元データといい，数列やベクトルとして表すことがある．
- 量的データのうち，とびとびの値をとるものを離散型，連続値をとるものを連続型という．
- 数量を表す量的データは和と差が意味を持つが，区分を表す質的データは和と差が必ずしも意味を持たない．

　今回の記事には測定尺度に関する話題が収まりきらなかった．そこで次回は，測定尺度という観点に基づいて量的データと質的データをさらに詳しく分類する方法を解説する．なお，重要な話題ではあるものの，次回の内容はやや高校数学の範囲を超えている．読み飛ばしても先の記事の内容について大筋を理解する分には差し支えないよう配慮するので，気持ちを軽くして覗いてみてほしい．

　次々回以降の記事では，いよいよ１次元データの解析手法について可視化と定量化の方法を順に解説する．