今回の記事では分数の計算の一種であるキセル算について解説していきます。算数の入試では,どれだけ簡単な問題をスムーズにこなし難しい問題に時間を割くことができるか,が肝心です。そのため本記事を通し,計算式への理解を深めていきましょう。

キセル算とは?
そもそもキセル算とはどんな問題を指すのでしょうか。キセル算とは,高校の数学で部分分数分解と呼ばれるテクニックを使う問題のことを指します。部分分数分解と言われてもほとんどの人がピンとこないでしょうが,この計算は分子を1とした分数の分母が隣り合った2つの整数のかけ算で表されるとき,その答えが分子を1・それぞれの整数を分母とした分数の引き算の結果と一致することを意味します。
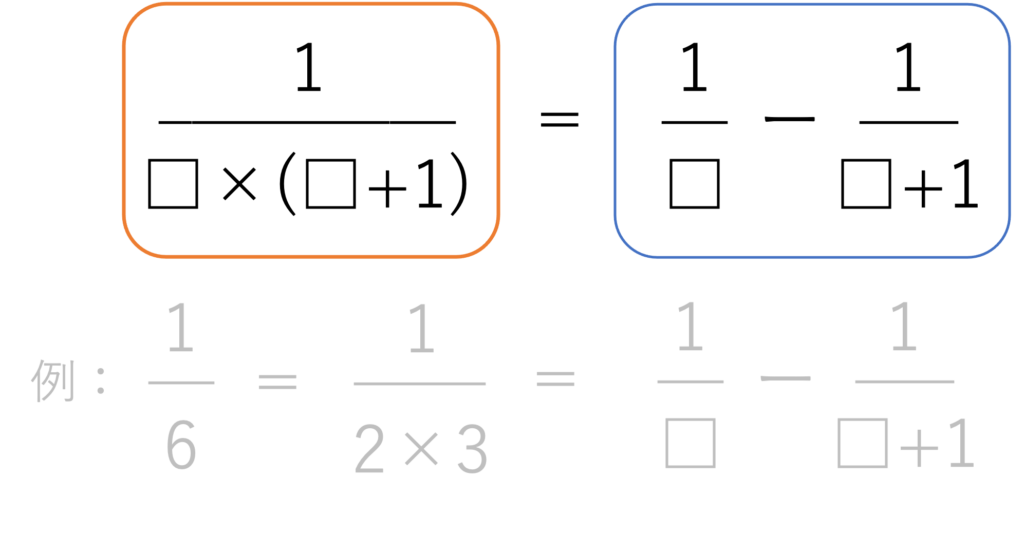
言葉だけだと難しいかもしれないですが,上のような図にすると部分分数分解,つまりはキセル算が何かを理解しやすいでしょう。この分解のテクニックを使って解く問題のことをキセル算と呼びます。 しかしこのように分解しただけでは1個の分数が2個に,かけ算が引き算になっただけのようにしか思えないでしょう。そのため以下では受験に出てくるような問題を取り上げながら,どうやってこの分解を使うのかを解説していきます。
分解のテクニックの使い方!
それではこのキセル算とは具体的にどういう形で受験に登場するのでしょうか。中学受験の算数では,次の図のようにいくつかの分数の足し算や引き算の過程で先ほど解説した部分分数分解を使う,というのがキセル算の基本の形になります。
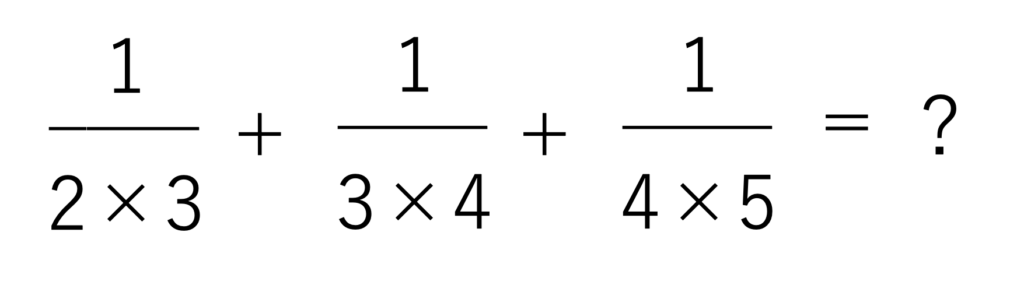
このような計算を何のテクニックも使わずに解いていると,とてつもない時間がかかってしまいますよね。上の問題で言うのであればそれぞれの分数の分母のかけ算をまず処理しないといけないので,1つ目の分母は6・2つ目の分母は12・3つ目の分母は20となります。しかし分母を計算したところで,3つの分母の異なる分数を通分して足し算するというのは大変骨が折れる作業です。計算ミスも起きやすいですし,貴重な時間を失ってしまいます。
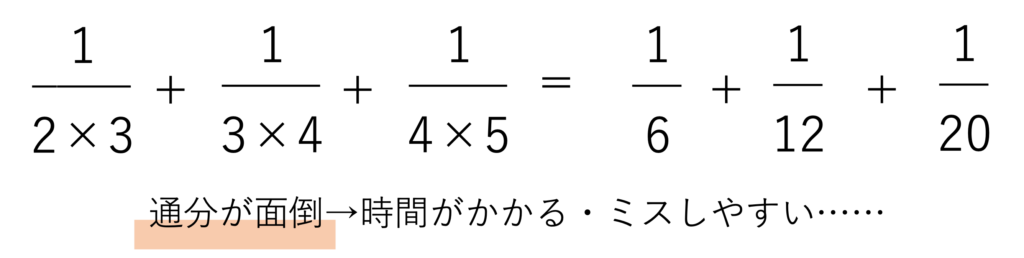
しかし部分分数分解をここで活かすと,計算をとても簡単にすることができるのです。上の問題を見ると,すべての分数の分母がかけ算になっていますが,その数が隣り合った2つの整数であることがわかりますよね。そのため3つの分数をそれぞれ分解して引き算の形に直すと,次のように変形することができます。

ここで部分分数分解をした後の式に注目してみましょう。分数が6つに増えて式も長くなったので面倒に感じる人もいるかもしれませんが,3分の1・4分の1という分数が2つずつ存在することがわかりますよね。そしてそれらの共通している分数にプラスとマイナスが1つずつくっついていることから,足し算の結果0が出来上がることがわかります。つまりこの長くて面倒に見える式は,2つの分数の引き算にできるのです。

このように部分分数分解のテクニックを使って,複雑な分数の足し算や引き算を簡単な2つの数の計算にしてしまおうというのがキセル算になります。ちなみにこの問題の答えは,最後に残った2つの分数の引き算を行うと,次のようになります。

キセル算は初見では解くことがほとんどできない問題ですので,キセル算と言う名前は聞いたことがなくとも,多くの受験生が一度は勉強したことがあると思います。しかし大抵の場合,どうしてこうなるのかを説明せず,2つの足し算・引き算になるということだけを教わりがちです。そのため部分分数分解というテクニックとセットで覚えておきたいところです。
なぜ「キセル」なのか?
ここまでキセル算とは何か・どうやって解くのかを解説してきましたが,ではなぜこの計算方法をキセル算と呼ぶのでしょうか。以下ではその命名の由来を見ていき,この記事を締めくくりましょう。このキセルというのは喫煙の道具のことであり,パイプのように中が空洞になっています。ここで先ほどのキセル算の計算過程を見てみると,2つの分数以外の分数は分解の結果消えてしまうので,式の真ん中が空洞になっているとみなすことができます。このような「空洞」という共通点があるため,キセル算と名付けられたというわけです。どの名前の問題がどういう計算をするかは直接受験に登場するわけではないのですが,テキストの索引で問題を探したりネットで検索をかけたりするときに有効です。そのため由来や名前のイメージと計算の内容を結びつけておくといいでしょう。
受験問題を解いてみよう!
ここからは実際に受験で出題された問題を取り上げながら,キセル算の応用的な解き方をご紹介していきます。しっかり解説もしていきますが,まずはここまで読んだことを活かして自力で解けるかチャレンジしてみましょう。
次の□にあてはまる数を答えなさい。
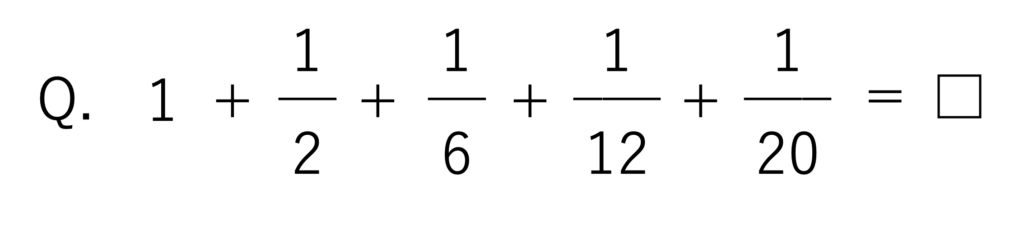
(愛知中学校(2022),一部改題)
問題解説
では問題の解説を行っていきます。この問題は分数の足し算ですので,全ての分母を通分して順番に足していって最後に訳文すれば答えを出すことができます。しかしいくつかの分数が続けて並べられているという形はキセル算であることが多いです。今回はキセル算の例題として問題を出題していますが,本番でも似たような形を見たらキセル算・部分分数分解ということを思い出してみるといいでしょう。
さてこの分数の式ですが,分母に注目すると2つの連続する整数のかけ算で表せるということが分かります。そしてそのかけ算の中身に着目してみると,2は1×2,6は2×3,12は3×4と1つずつ数が飛んでいることも明らかになりますよね。

ここで分数の分母が隣り合った整数のかけ算になっているので,部分分数分解のテクニックが使えそうですよね。そこで,この分母を2つの整数のかけ算に表した分数を分解し,式を引き算の形で書き換えてあげましょう。式を変形させると次の図のようになります。
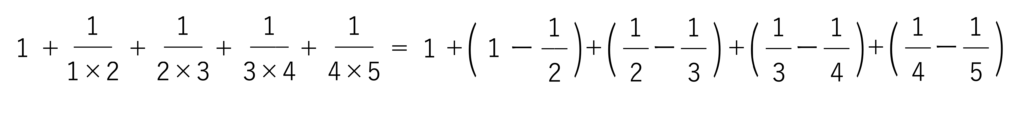
そしてこの図を見ると,先ほど解説の欄で取り扱った例題のように,同じ分数が符号を変えて存在することが分かります。したがって計算の結果0が3つ生まれ,1が2つと5分の1が1つだけ残って計算式を大幅に簡単にすることができるのです。このことから残った分数を引き算でまとめると,答えは次の図のようになります。

キセル算では「これは部分分数分解を使えば楽だな」ということに早く気づけるかどうかが重要になってきます。そのためたくさん分数の問題を解いてテクニックに慣れておく必要があります。はじめのうちはどんな分数の問題でも,一旦分解してみれば楽に解けるかも…?と考えて寄り道しながら計算してみるといいでしょう。
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。
まとめ
今回の記事ではキセル算という計算式に着目し,その定義や計算方法について解説していきました。分数の計算は中学受験では落としたくない問題です。スムーズに確実に正解できるよう,今回お教えしたことを活かして更なる勉強に励んでいただけますと幸いです。よろしければ以下の記事や書籍を参考にしてみてください。
(ライター:大舘)

















