今回の記事では,体積や比率など複数の単元の内容が絡んでくる水量変化とグラフという問題について解説していきます。
この基礎編の記事では,主にこの範囲ではどのような特徴の文章が登場するのか,どうやって答えを導いていけばいいのか,といった事柄を取り扱っていきます。
この範囲は難しい問題が出題されやすいので,早めの対策が必須です。よろしければ本記事で対策を進めていただけますと幸いです。
Contents
「水量変化とグラフ」とは…?
まず水量変化とグラフとはどのような問題なのかを押さえていきましょう。
この分野の問題は,立体の容積という空間図形の特徴と水の流れるペースという速さの特徴を兼ね備えています。そのため初めてだとなかなか解きづらい問題が多いです。
具体的な問題設定はこの後確認していきますが,基本の流れは水の入る容器の中に一定のペースで水を入れていき,その貯まり具合をグラフとの関係で考えていくというものになっています。
そのためもし立体あるいは速さといった範囲の内容が得意ではない人は,その辺りの単元を振り返りながら読んでみてもいいかもしれません。
「水量変化とグラフ」の3つの特徴を掴もう!
それではここからは問題の特徴を詳しく押さえるために,例題を見ながら中身を深掘りしていきましょう。この単元では次のような問題が出題されると覚えておいてください。
下の図のようなかたちをした直方体の水そうがあります。この水そうに毎分20リットルの割合で蛇口から水を入れたときの時間(分)と水面の高さ(cm)の関係をグラフに表しなさい。
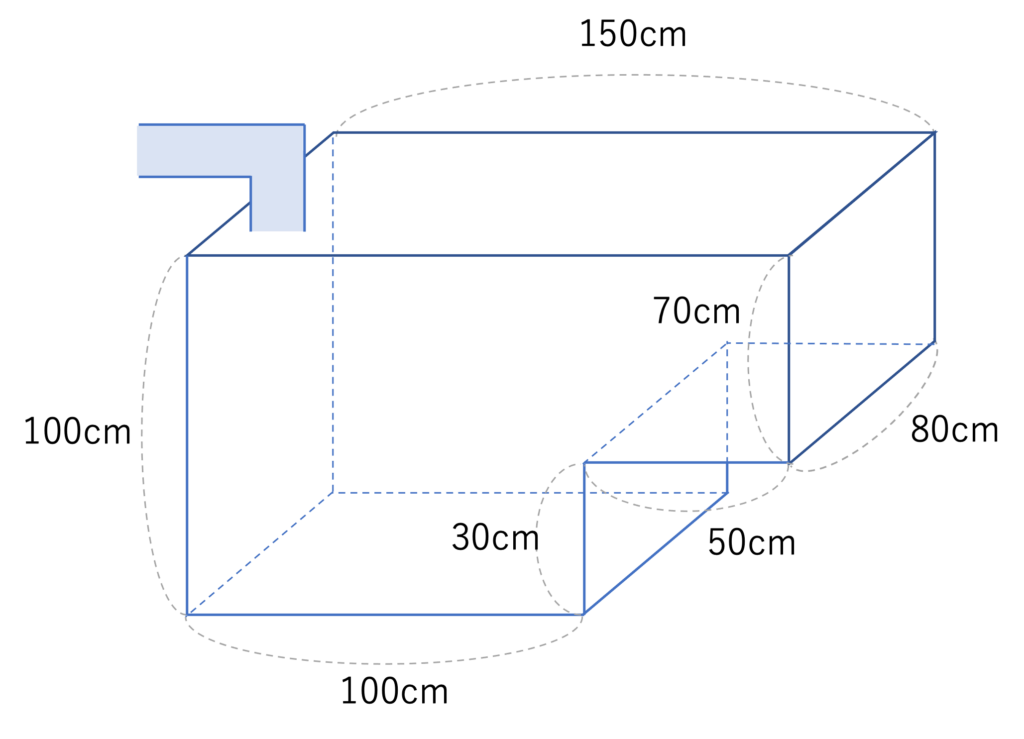
この問題はグラフを書くことをゴールとしていますが,問題によってはグラフから水の流れるペースを考えたり,グラフから立体の容積を考えたりすることもあります。
今回は基本編ということでこの例題を使用していきますが,今後の記事では別パターンの出題についても取り扱いますので,よろしければそれらの記事も併せてご活用いただけますと幸いです。
さて問題の分析に移りましょう。1つ目に特徴として挙げられるのが,やはり立体の存在でしょうか。
この問題でもたて・よこ・高さが与えられていて,かつ少し窪んだ形をした立体が登場しています。このほかにも仕切りがあったり段が増えていたりとさまざまなパターンの出題が考えられますが,後々解説するようにどれも注意するべき要素は同じです。
それゆえまずは,変な形の立体があれば水量変化とグラフからの出題かもしれないという予測を立てるということを意識できるようになるといいですね。
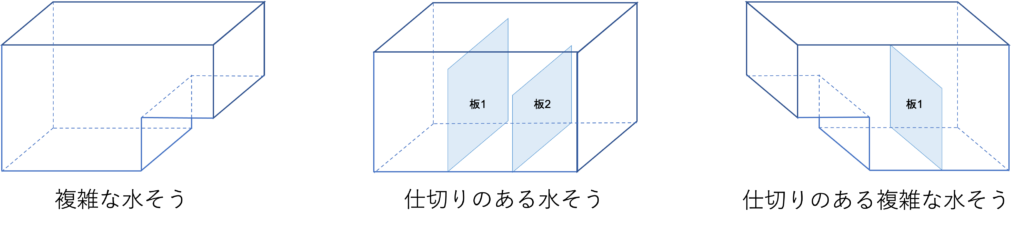
そして2つめの特徴としては,水を入れるというシチュエーションが挙げられます。
水量変化なので当然のことではありますが,水そうに水を入れることで問題が始まりますので,そのような単語もしくはそのときの割合が文中に入っていたらこの分野からの出題と決めてしまってもいいでしょう。
また問題によっては,入れるだけでなく水を抜くという設定も登場します。その場合計算が複雑になり,入れる量と抜く量の差を考える必要があるので注意が必要となります。
最後に3つめの特徴ですが,これはグラフの存在になります。今回はグラフを答えとして書く問題ですので,グラフそのものは載っていません。
しかし受験で登場するような複雑な問題は大抵がグラフの読み取りありきの構成をとっています。それゆえ書くという意味でも読むという意味でも,グラフへの理解度は解答を導き出す1つのキーポイントだと言えるでしょう。
例題を解いてみよう!
それではここからは例題を解いてみましょう。使うのは先ほど登場させた問題です。実際に蛇口をひねったら水はどのように増えていくのかということをざっくり頭で考えて,その結果から予想を立てて時進めていくといいでしょう。
下の図のようなかたちをした直方体の水そうがあります。この水そうに毎分20リットルの割合で蛇口から水を入れたときの時間(分)と水面の高さ(cm)の関係をグラフに表しなさい。
例題の答え合わせをしよう!
それではここからは問題の答え合わせに移ります。今回の問題のような水量変化とグラフからの出題では,次のような3つのポイントを抑えることで正しい答えを導くことができます。
もちろん答えが出れば何も問題はありませんので,下のステップに必ず従うはありませんが,一つの目安として覚えていただけますと幸いです。
ポイント① 立体を平面に置き換える!
まず重要なのは,立体を平面に置き換えるということです。
先ほども申し上げましたが,水量変化とグラフの問題では水そうの中の水の貯まり具合が聞かれます。しかし水そうという立体における水の動きはイメージしづらいので,一度その貯まり具合がイメージしやすい形に中身を整理する必要がありますね。
そのために立体を平面に置き換え,どのように水位が変わっていくのかを想像するというわけです。
例えば今回の立体にはくぼみが存在しますが,そのくぼんだ部分が分かりやすいように平面に書き起こすと次のような形を描くことができます。
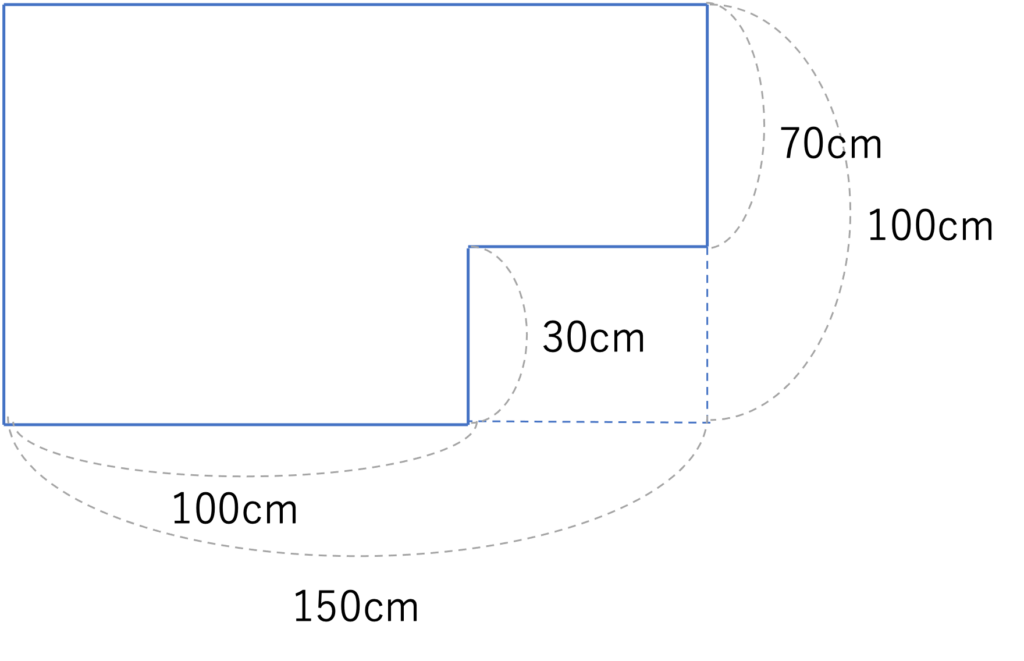
このように書き換えると,平面のときより水の動きがイメージしやすいのではないでしょうか。
今回の問題だと水を入れるペースは1分間に20リットルと指定されていますが,初めにこの水はくぼんで底面積が小さくなっているところに貯まり,水面が30cmを超えると底面積が拡大するため水位の上がり具合が緩やかになっていくことが頭の中で描きやすいと思われます。
またイメージのしやすさだけでなく,立体を平面に起こすことで情報が書き込みやすくなるという利点もあります。
唯一の弱点としては図形の奥行き(今回なら80cmという要素)だけ見えにくくなってしまうので,その点だけ気をつけましょう。
ポイント② ペースの切り替わりを抑える!
さてポイント①を通して水の貯まり具合が確認できました。今回の問題だと水位30cmを境に貯まるペースが変わることが分かりましたね。
この問題は図形がシンプルなため分かりやすいとはいえ,この攻略法は推奨変化とグラフという単元の全ての問題に有効にはたらくので覚えておくといいでしょう。
ここで,いま高さ30cmの地点で切り替わるということを確認しましたが,ここからは30cmという要素を意識しつつ,ペースの切り替わりの細かい部分を確認していきましょう。具体的にはどれくらいのペースで初めは貯まっていき,何分の地点で30cmに達し,そこからはどれくらいのペースに変わるのかといったことを計算していきます。
これらの情報はグラフを書く上で欠かせませんが,グラフを書く問題以外でも必須の要素ですので,必ず計算する癖をつけておきましょう。
まず初めに30cmに達するまでのペースを計算していきましょう。ここで容積の考え方について振り返っておくと,立体の容積はたて×よこ×高さで計算できましたね。たて×よこの部分を底面積と言ったりもするこの計算式ですが,今回取り扱う図形のうち30cmまでの部分の容積を計算すると,たて×よこ×高さ=100cm×80cm×30cm=240000cm3となります。
ここで問題文ではこの容積を1分間につき20リットル=20000cm3ずつ埋めていくという指示が与えられているので,30cmの部分までを貯めるのにかかる時間は240000cm3÷20000cm3=12分となります。
ちなみに,今回のグラフの作成には必要ないですが,このときの1分あたりに上昇する水位についても考えておきましょう。1分あたりに追加される水の量が20リットルであるとき,その20リットルの水は当然ですが水位が均等になるように貯まっていくので,入れる量を底面積で割ってあげることで1分あたりの上昇分を計算できますね。
いま1分あたりに上がる水位を○とすると,80cm×100cm(底面積)×○=20000cm3という式が立てられます。この式を解くと○=2.5cmとなるので,30cmの部分までは1分ごとに2.5cmずつ水位が上昇していくと求められますね。
ではここからは同様の手順で,30cmの地点から立体の一番上である100cmの地点までの70cmにおけるペースを考えていきましょう。
この部分の容積は,30cmの部分までと比較すると底面積の値が大きくなっていることに注意すると,150cm×80cm×70cm=840000cm3となります。この立体に毎分20リットル=20000cm3ずつ水を入れていくわけですから,かかる時間は840000cm3÷20000cm3=42分となります。
また1分あたりに上昇する水位についても考えてみましょう,いまその値を□cmとすると,150cm×80cm(底面積)×□cm=20000cm3という式が成り立ち,これを解くと□の中身は6分の1となることから1分ごとに6分の1cmずつ水位が上昇すると求められます。
ポイント③ 対応する形で解答する!
ここまでのポイントによって図形の平面図の作成により水の流れをイメージし,具体的にどのようなペース・時間で溜まり具合が切り替わっていくのかを求めることができました。
ここまで求めた情報を先ほどの図に落とし込んでいくと,次のように整理することができます。このように求めた値をまとめていくのも文章題では重要です。見直しのしやすさという意味でも,計算の記録は分かりやすく整理する癖をつけましょう。
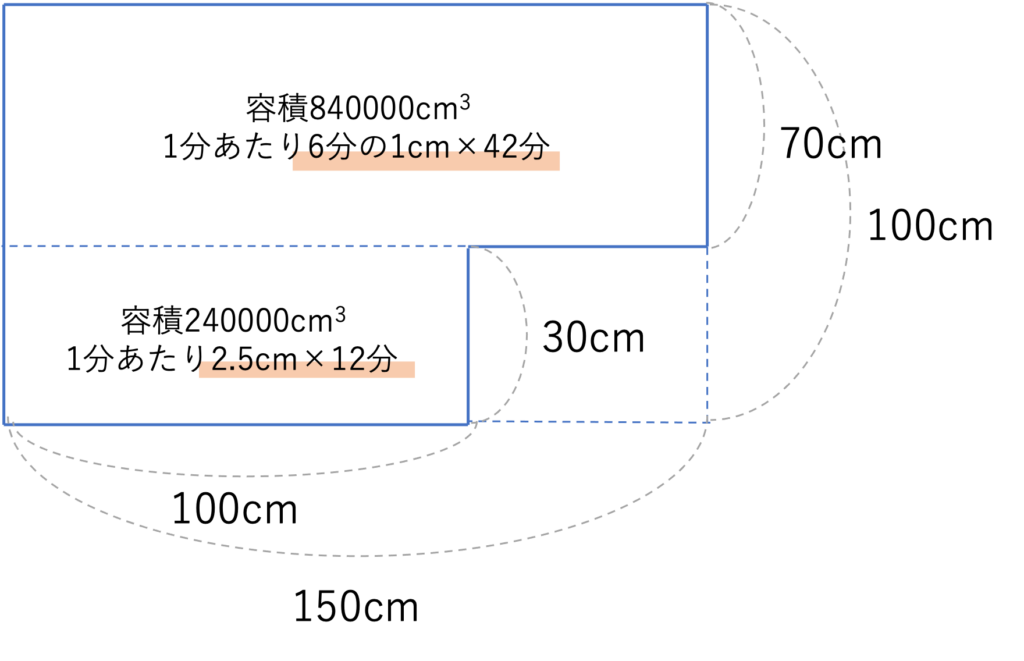
この図から,水は初めのうち1分間に2.5cmの速さでかさを増していき,12分経ったところで30cmに達するため,1分間に6分の1cmのペースに変わり42分かけて最高水位まで到達することが分かります。
そしてこれらの要素がまとめられたので後は求められている形で答えを出しましょう。
今回は時間と高さのグラフにまとめるという指示がありましたが,問題によっては高さや速さを答えとして導くものもあります。何が問われているかに注意し,最後まで気を抜かずに解き進めましょう。
グラフが答えになっているということで,ここで基礎の確認を含めグラフの書き方を振り返りながら答えを考えていきましょう。まずグラフに必要なのは縦軸と横軸です。
今回は時間と高さ,という指示があったので次のようにグラフの基盤を作りましょう。
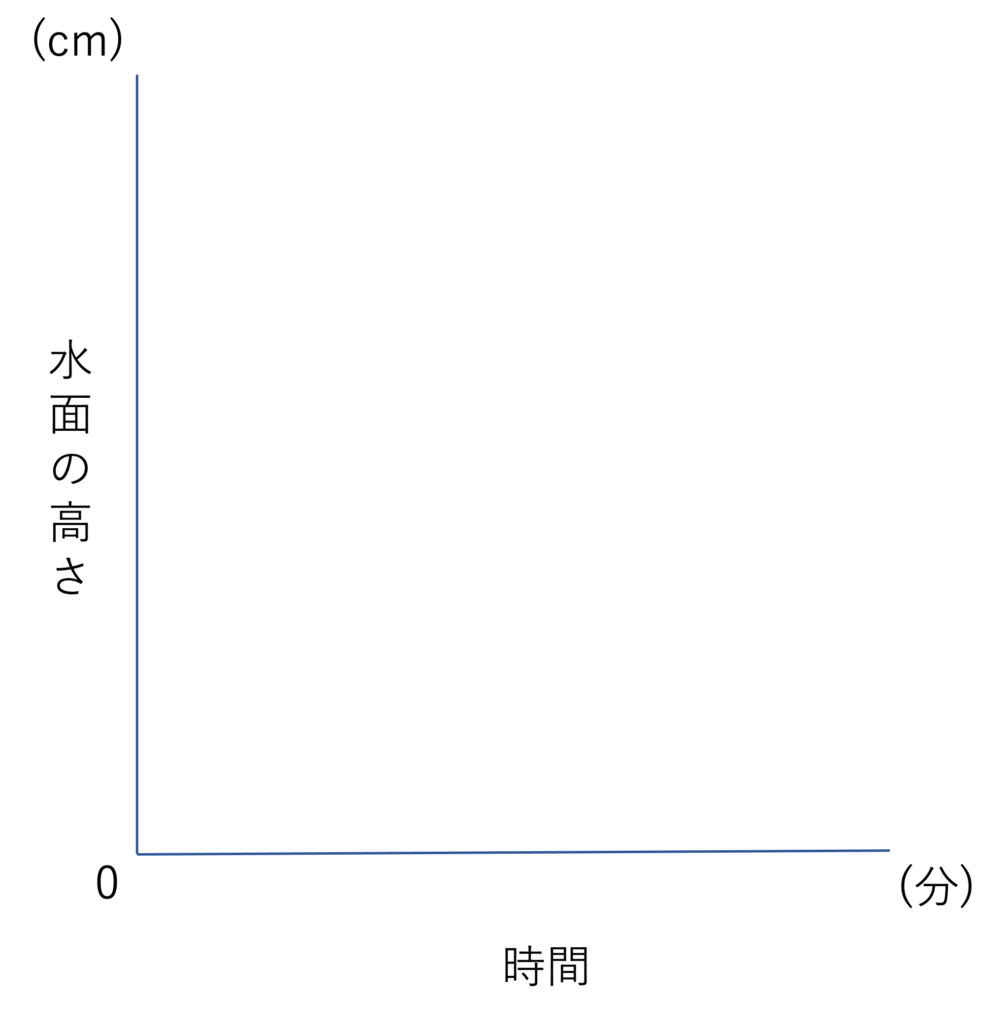
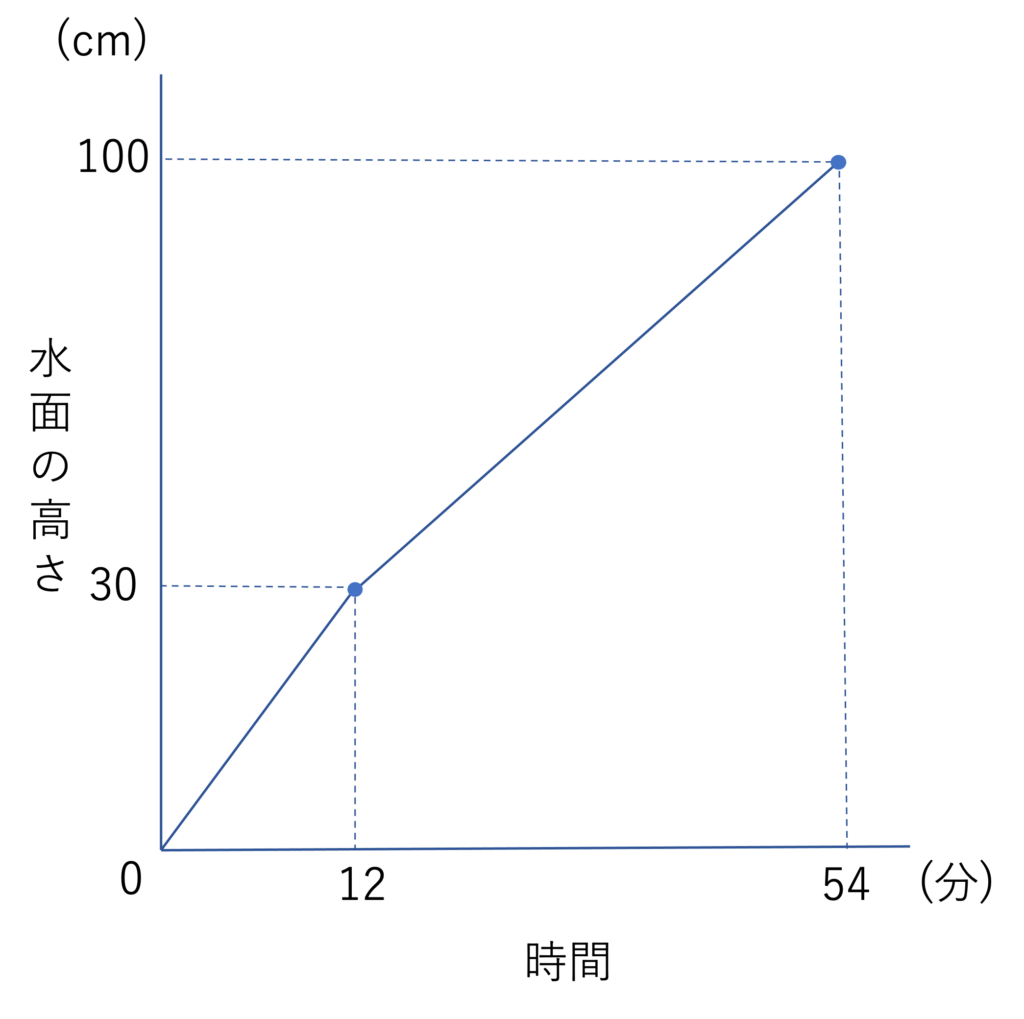
次にグラフの中に点を打ち込み,それらを繋いでいきましょう。今回は12分・30cmの地点までは一定のペースで水位が増えていき,そこから42分後に70cm分増える,つまりは54分・100cmの地点で最高点に到達することが分かっていますので,その2点を取って繋ぐことで答えのグラフを作ることができます。
A.
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

まとめ
- 水量変化とグラフとは「水の入る容器の中に一定のペースで水を入れていき,その貯まり具合をグラフとの関係で考えていく」問題のこと!
- 解答のヒントは立体を平面に置き換えることで見つけよう!
- 貯まるペース・時間・ペースの転換点の3つの要素に注目しよう!
終わりに
今回の記事では立体・速さという2つの単元が関わる分野としての「水量変化とグラフ」問題に焦点を当て,その解き方を解説していくものでした。
この単元はなかなかはじめのうちは解くのが難しく感じることが多いでしょうが,しっかり解けるようになるだけで周りと大きな差をつけることができます。
そのためまずは解答スピードを気にせず正確な答えを出すことを意識して取り組んでみるといいでしょう。本記事が今後の学習のお役に立てば幸いです。

















