今回の記事ではトーナメントというものの受験算数での扱われ方について解説していきます。
本記事を執筆している2022年冬現在,サッカーのワールドカップが世間では盛り上がっていますが,このようなスポーツの大会等,ただ一人の優勝者を決めるための大会で使われがちな仕組みがトーナメント戦です。しかし,日常的に見かけるものであるトーナメントも,ひとたび受験問題として登場すると苦戦してしまいやすいものです。むしろ対策がおざなりになりがちな分,周りに差をつけられやすい分野だとも言えます。そのため本記事で対策を進めていただければ幸いです。
Contents
「トーナメント」とは?
そもそもトーナメントとはどのような仕組みのことを指すのでしょうか。特にスポーツなどに疎い人はイメージがつきにくいかと思われますので,今一度解説させて頂こうと思います。既にご存知の方は次の章まで飛ばしてしまってください。
トーナメントとは,簡単に言ってしまうと,勝ち残り形式で優勝を決める仕組みのことを指します。英語のtournamentは単に競技大会といった意味なのですが,日本語で「トーナメント」といった際には,各競技者(又はチーム)が一対一での対戦を行い,負けた側は脱落,勝った側はまた次の試合へ……という工程を繰り返し,最後に残ったものが優勝,という仕組みのことを指すことがほとんどです。
本題は算数の側面からの解説ですので深くは説明しませんが,一度でも負けてしまうと次のチャンスがないことから,全ての試合に緊張感があり無駄な試合無く盛り上がるが,反面一発勝負で純粋な実力を測るのには向かない,という特徴があります。
一般的に,トーナメントの参加者がはじめに対戦する1対1の試合のことを1回戦,その次の試合を2回戦,……と呼んでいき,最後に残った試合を決勝戦と呼びます。ただし以下で解説するように,必ずしも1回戦ですべての参加者が対戦を行うのではなく,中には2回戦からの参加となるシードという枠も存在します。このようにだんだん残りの数が減っていくという数字の変化の仕方やシードが出てくるときの条件などを考える上で,算数で使うような頭の動かし方が必要とされるため受験でも登場するというわけです。
なお似たような言葉として受験に登場しがちなリーグ戦という仕組みも存在します。今回はリーグ戦には着目しないものの,どのような違いがあるかを述べておきましょう。
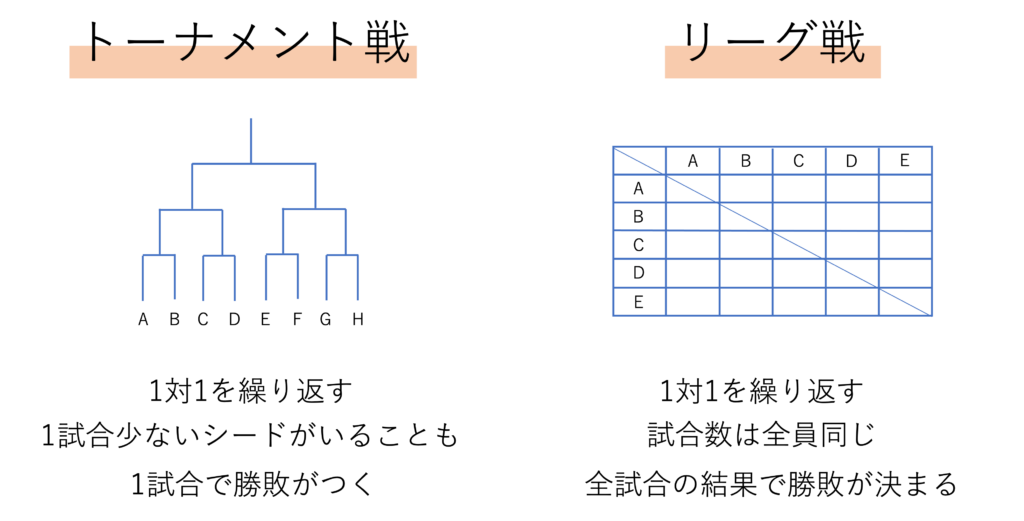
先ほど述べたようにトーナメントとは1対1を繰り返していくシステムのことを指しますが,リーグ戦も1対1の試合を繰り返していくという仕組みであり,その点は共通していると言えます。
しかしトーナメント戦と異なるのは,リーグ戦は他の全参加者と対戦して,優勝を決めるという点です。このような全員と当たって対戦するという特徴から,総当たり戦と呼ばれることもあります。
このリーグ戦(総当たり戦)の最大の利点は,負けたらおしまいのトーナメントと違って,負けても次の試合,つまり挽回のチャンスがあるという点です。ただし,参加人数が増えるほど加速度的に試合数が多くなってしまうという欠点もあります(5人だと計10試合だが,10人だと計45試合!)。リーグ戦も受験で出題されやすいので,何試合あるのか・どうなれば優勝するのか,など日頃から大会を見る・大会に出るなどの際に意識してみるといいでしょう。
中学受験におけるトーナメント
ここからは受験におけるどのようなシーンでトーナメントというものが登場するのかについて解説していきます。
はじめに,トーナメントは2つの分野で出題される傾向にあります。1つ目は場合の数という単元です。場合の数というのは,ある事柄に関して起こりうる可能性のある状況の数のことを指します。
この言い方だと少し難しいかもしれませんので,サイコロをふるときのことを考えてみましょう。サイコロを振った時,出る目は1から6のいずれかですよね。しかし投げるまではどの目がでるかは分からないので,サイコロをまだ振らないうちは出る目に関して6通りの可能性があるわけです。
このように,どのような可能性がどれくらいあるかにまつわる問題が登場するのが場合の数という単元なのですが,トーナメントというのはこの単元と絡めて登場することが多いです。考えられる問題としては,トーナメントである特定の2人の参加者が対戦する可能性だったり,1回戦で考えられる組分けの可能性だったりがあります。この単元からの出題では,数字を使った頭の動かし方が必要とされます。
2つ目は論理と推理という単元での出題です。論理と推理という単元は,いくつかの情報に基づいていろいろな条件を絞り込んで1つの答えを出すという範囲のことを指します。ただし,この説明だけでは「普通の算数の文章題でも同じでは?」と思われたかもしれません。しかし算数の中でもこの推理と論理という範囲にしかない特徴として,数字が全く関係なく,すべての説明が文章で与えられるということです。いわば謎解きみたいなものですね。そのため先ほど説明した場合の数が算数そのものといった頭の動かし方をしなければならない単元だったのに対して,この論理と推理では言葉を巧みに操って内容を紐解いていく力が必要となります。この分野におけるトーナメントの問題としては,「AさんはBさんに買ったが3回戦で負けた」「BさんはCさんとは戦わなかった」などの条件をもとに,トーナメントのどこにだれがいたかを推測していく,といったようなものが出題されがちです。クイズに近い,と言った理由もこのような出題傾向にあります。
【すべての試合の回数】を考えてみよう!
ではここからは出題傾向の話から,トーナメントの性質の話へと転換していきます。まず見ていくのはトーナメントというもので起こる試合の数についてです。トーナメントの問題で特に聞かれがちなのがこの「試合の数」というもので,どのような数字が使われても解けるようにしっかり暗記しておきたいところですが,まずは参加者が2人,3人,4人と増えていったときの試合の数の増え方を見ていきます。
はじめに参加者が2人の場合,1回の試合で優勝・準優勝が決まるので,すべての試合は1試合になります。次に参加者が3人の場合,先ほど説明したシードというものが1人出てきますので,はじめに1回戦で3人のうち2人が戦ったあと,その勝者と戦わなかった1人が試合をして優勝が決まります。つまり必要な試合数は2試合ですね。そして参加者が4人のとき,4人を2人ずつに分け2試合で勝者を2人出したあと,3試合目で勝った者同士を戦わせるので,優勝を決めるまでに必要な試合数は3試合となります。このように2人のとき1試合,3人のとき2試合,4人のとき3試合,……と見ていくと,参加者が□人いるとき試合数は(□-1)回となるという関係性を見出せるのです。
なぜこのような関係性が成立するのでしょうか。それはトーナメントが1対1の試合で勝者を決める,というシステムであることと関連しています。トーナメントにおいて,1回の試合ごとに勝者は1人現れ,敗者も同じように1人現れます。このうちの勝者はまた別の勝者と戦い,そこでもまた1人が敗者になるので,つまりトーナメントでは1回の試合ごとに1人が脱落していきますよね。そして1人の優勝者を決めるためには,参加者のうち優勝者以外の全員を敗者にしなければいけないということから,必要な試合数は全参加者から最終的な勝者の数を引く,つまり参加者の数-1で計算することができるというわけなのです。

【優勝までの試合回数】を考えてみよう!
ではここからは優勝までに必要な試合の回数に視点を変えて解説を行っていきます。なお分かりやすいように解説していくため,ここではシードがいないものとしてトーナメントについてみていきましょう。ここでは勝つまでの試合が○回戦まであると考えた上で,○の中身が増えていくと参加者がどう増えていくか考えていきます。
まず1回戦まであるとき,つまり優勝するまでの試合の回数が1回のとき,参加者は当然2人ですよね。次に2回戦まであるとき,決勝戦に残るのが2人であり,その2人の枠を決めるための1対1の試合が2回行われるわけですから,4人の参加者がいることになります。次に3回戦まであるとき,2回戦までのとき考えた4人を決めるための試合がそれぞれの参加者についてもう1回分必要なわけですから,8人の参加者がいないと成立しません。このように関係を追っていくと,○回戦まであるとき2を○回かけた分の人数の参加者がいることが分かります。
この関係性が成立する理由は,トーナメントでは1回戦につき参加者が半減するからです。先ほどトーナメントの1試合では参加者が1人勝ち残り1人敗退するということを説明しましたが,このことから全ての参加者が1回ずつ試合に参加することで,試合が行われた数の半分の参加者が勝って半分が負ける,つまり参加者が半減するということが説明できます。これは裏を返せば,ひとりひとりの試合の数を1回増やすごとに全体の参加者が倍になるという風に言えますね。そのため優勝者が1人,決勝戦が2人,準決勝が4人,……と参加者の数は○回戦の分まで倍増していくわけです。

【シードの数】を考えてみよう!
最後にシードの数の計算の仕方をお教えしていきます。先ほどシードがいない状況では,参加人数は,2を優勝するまでの試合の数の分だけかけ算することで計算できるとご説明しました。ではその延長としてシードがもし出る場合,そのシードは何人になるのでしょうか。
先ほど説明したように,大前提としてシードを作らないときの参加者の人数は2を優勝までの試合数の分だけかけた値になります。このことから,2を優勝までの試合数の分だけかけ算した値がシードのいないときの参加人数になる,という逆の関係も成立すると言えますね。ここで2を何回かかけた数というのは2,4,8,16,32,……となりますが,当然のことながら色々な大会の参加人数がこれらの数になるとは限りません。このような場合トーナメントでは,はじめに参加人数よりも大きな,2を○回かけた数を用意します。例えば参加人数が5人だった場合,先ほど挙げた2,4,8,16,32,……という数の中で5よりも大きな数である8という数を用意する,と言ったような感じです。
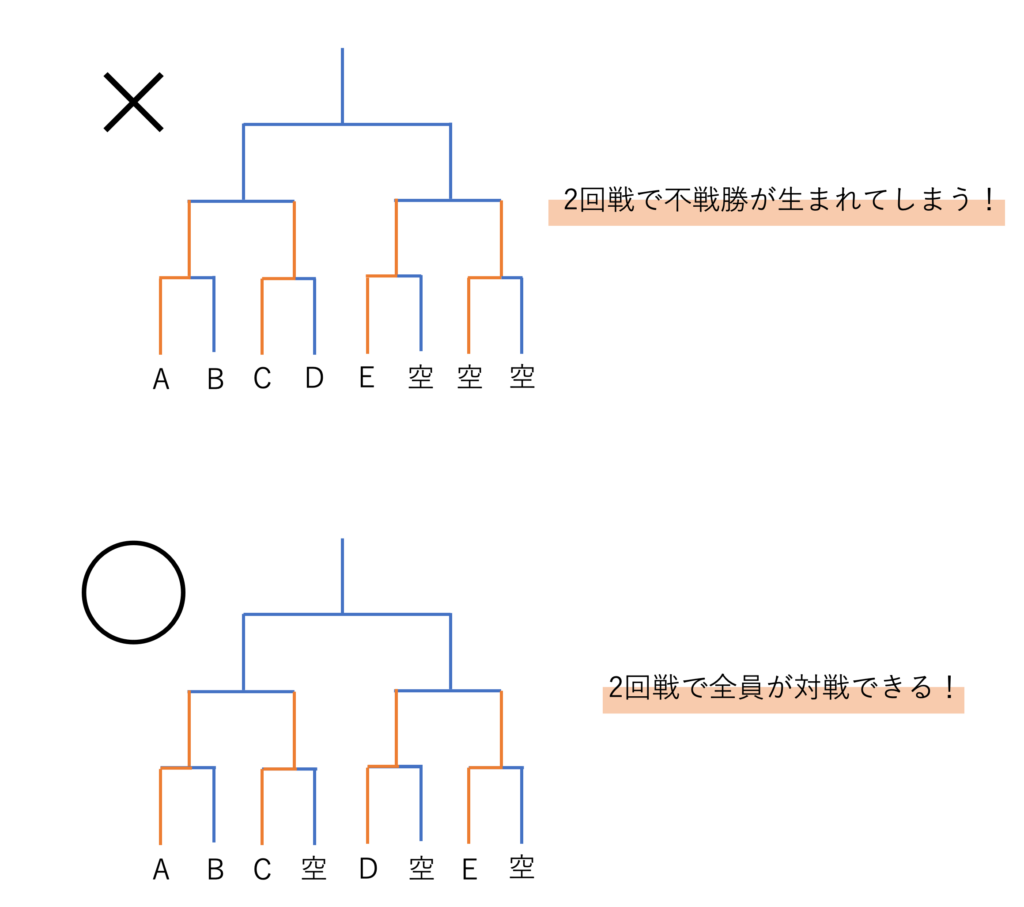
そして上の図のように5人+空欄3つという内訳の8つの枠が用意できるわけですが,このままではトーナメントが行えないことが分かります。それは空欄同士では戦うことができないからです。空欄同士での対決をしてしまうと,勝ちも負けも出でこないことになりますが,このままだと2回戦でも空欄が現れてしまいます。シードというものが1回戦で参加人数を揃えて2回戦以降で全員を戦わせるためのものだったのに,これではそのシステムが崩れてしまいます。そこで2回戦で空欄が出ないように,空欄は参加者と向かうようにトーナメントを組む必要がありますよね。
このように組むと,空欄の部分が不戦敗のような形で消え,2回戦で空欄が全くでないことが分かります。このことからシードの数とは1回戦における空欄の数と同じであることが明らかになり,つまりシードの数とは,参加人数より大きな2を○回かけた数-参加人数で計算できるということになります。よくありがちな間違いとして,参加人数より小さい2を○回かけた数で考えてしまう人がいるので注意しておきましょう。

受験問題に挑戦してみよう!
それではここからは実際に受験で登場したトーナメントの問題にチャレンジしてみましょう。今回は場合の数からの出題をピックアップしました。論理と推理から出題されている過去の受験問題もあるのですが,前述したようにそちらはクイズの成分が強く,コツというよりは日頃から思考力を養ってきたかが問われるものですので,今回はよりテクニックが重視される場合の数に絞っている,というわけです。それではまずは自分の力で解けるかどうか,チャレンジしてみましょう。
次の□に適する数を求めなさい。
52チームが参加する大会は,トーナメント戦で優勝が決まります。このとき,1回戦が不戦勝のチームは□チームあります。
(鎌倉学園中学校(2014),一部改題)
問題解説
それでは上で挙げた問題の解説を行って,本記事を締め括っていきましょう。この問題はシードの数に関する問題でした。そのため先ほど説明した式から問題を簡単に解くことができますが,解説の振り返りとして考え方についても触れておきましょう。
まず参加者の数に注目しましょう。参加人数が2を○回かけた数であれば,シードがないトーナメントになりますが,今回は52ということで当てはまらないのでシードが絶対に出てきます。そのため参加人数より大きな,2を○回かけた数を用意しましょう。ここでは2を6回かけた数である64が,52より大きい,2を○回かけた数として考えられますね。
そしてこのとき64個のトーナメントの枠が出来上がるわけですが,参加チームは52チームであることから,64-52=12個の空欄ができてしまいますよね。そして前の章で説明したように,空欄は参加者と向かうようにトーナメントを組まなければいけないことから,シードの数は空欄の数に一致するという関係がありました。そのためシードの数は12チームとなり,答えは12チームとなります。この問題は何も知らない状態で考えるのは難しいですが,法則を知っているだけで簡単に解けますよね。中学受験ではこのように知っている/知っていないが勝敗を分ける問題が多く出てくるので,トーナメントに限らず幅広い知識を吸収していきましょう。
A.12チーム
まとめ……の前に
『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓

終わりに
今回の記事ではここまで,トーナメントというシステムを受験算数と絡めて解説していきました。繰り返しになりますが,トーナメントというのは日常生活で登場する分,つい対策がおざなりになりがちなところがあります。もちろん図形問題や文章題より優先度は低いですが,少しでも問題を取りこぼさないよう,きっちり対策しておきましょう。本記事が今後の学習のお役に立てば幸いです。
(ライター:大舘)