【高校１年生～大学生】「データの分析」を基礎から徹底解説！

第1回　尾崎　

Contents

1 はじめに
- 1.1 「データの分析」という単元の位置づけ
- 1.2 【補足】この連載記事のねらい
2 記述統計学の概観
- 2.1 記述統計学の目的
- 2.2 記述統計学の方法
  - 2.2.1 可視化のアプローチ
  - 2.2.2 定量化のアプローチ
3 まとめ
4 おすすめ記事
5 参考文献

はじめに

　高校の数学Iで学ぶ単元の１つに「データの分析」がある．データを適切に整理・要約する方法についての応用的な数学だ．この単元と数学Aの「場合の数と確率」で習得する知識は，ともに数学Bで「統計的推測」を学ぶときの基礎となる．

「データの分析」という単元の位置づけ

「データの分析」で学ぶ内容は，記述統計学という分野に含まれる

　勉強をはじめる前に，少し学問の世界を俯瞰してみよう．数学Iの「データの分析」と数学Bの「統計的推測」はいずれも，数学的な手法を応用することでデータから何らかの知識を得ることを目的としており，統計学（statistics）という学問の中に位置づけられる．特に「データの分析」が記述統計学（descriptive statistics），「統計的推測」が推測統計学（inferential statistics）という領域の導入部分にあたる．

　後続の2.1節でもう少し詳しく説明するので，ここではそれぞれの分野について簡単に言及するだけにとどめておく：

「データの分析」（数学I）
記述統計学：データを適切に整理・要約することで標本の性質について解釈可能な情報を抽出しようとする数学．
「統計的推測」（数学B）
推測統計学：確率論のアイディアを用いて，標本が持つ性質からその背景にある母集団の性質を推測しようとする数学．

「データの分析」で学ぶ知識は，きっとあなたの役に立つ

Left to be written：統計学の観点は現代の科学的手法において欠かすことができない；統計学が重要なのは別に科学者に限った話ではない；実際に大学の教養課程や専門課程では文系・理系を問わず多くの学生が「統計学」を学ぶことになる；数学Iの「データの分析」は，そうした実応用上きわめて重要な学問の入り口なのだ．

【補足】この連載記事のねらい

　この連載では「データの分析」で学ぶ内容を中心に，記述統計学の基礎を解説する．具体的には次の語をキーワードとして話を進めていく：度数分布とヒストグラム，代表値，散布度，箱ひげ図，基準化，相関，回帰．

　筆者が想定している主な読者は，例えば次のような方々だ：

「データの分析」を初めて学ぶ高校生１年生の皆さん
「データの分析」を復習してさらに理解を深めたい高校生２，３年生の皆さん
大学の教養課程や専門課程などで初めて統計学を学ぶ大学生の皆さん

　初めて「データの分析」を学ぶ方でも記述統計学の考え方を易しく習得することができるように，一貫して丁寧な説明を心掛ける．その一方で，既習の方にも新たな発見があることを願い，やや発展した事項や推測統計学を意識した事項についても言及していきたい所存である．

　そのため時には一般化を目的とした少し抽象的な表現や，やや先取りした内容が含まれることがあるかもしれない．初学者にとって難しいと思われる部分については「発展」や「補足」事項の扱いとして，読み飛ばしても大枠が理解できるように配慮するから安心してほしい．またそれぞれの記事はなるべく，それ一つで完結した内容とするので，気になる項目だけを辞書的に読んでいただくこともできる．

　気軽に覗いてみていただき，記述統計学の雰囲気を掴むだけでも皆さんのお手伝いができれば幸いだ．

記述統計学の概観

記述統計学の目的

記述統計学はデータを良く知るための素朴な学問だ

　我々の身の回りには，測定によってもたらされたあらゆる記録の集まり，すなわちデータ (data) があふれている．この連載ではデータを適切に整理・要約することによって，そこから解釈可能な情報を取り出そうとする数学（記述統計学，descriptive statistics）について紹介しよう．具体的には，手元にあるデータの分布はどのようになっているのか（どのくらいの数値のデータがどれくらい豊富にあるのか），真ん中の値はいくつなのか，値の散らばり具合はどうか，といったことを調べる方法について学ぶ．

　難しそうに聞こえるだろうか？

　大丈夫，心配は要らない．実のところ皆さんはすでに記述統計学に触れたことがあるのだ．

　たとえば，リンゴ5個の重量をはかった結果，

$$ 295, \quad 312, \quad 280, \quad 292, \quad 301 \, (\rm{g})$$

というデータが得られたとする．「リンゴって，どれくらいの重さ？」と聞かれたとき，簡潔に説明できるよう，このデータの真ん中の値をリンゴの重量の代表的な値として採用しよう．そのためには平均値（算術平均）を求めると良さそうだと思いつく：

$$ \dfrac{295+312+280+292+301}{5}=296 \, (\rm{g})$$

何の変哲もない当たり前の計算に感じるかもしれないが，これぞデータの記述．記述統計学の目的は「データそのものをよく知る」ことであり，ほとんどの解析がこうした素朴な発想に基づいている．

記述統計学は統計解析の第一歩である…

　さてデータを記述することによって得られた情報は，たとえば確率のアイディアと組み合わせることで，その標本の源となった母集団が持つ未知の性質について探るため利用される．このような分野は記述統計学に対して推測統計学（inferential statistics）と呼ばれている．

　記述統計学では，たくさんのリンゴの重量を調べたデータについて，先ほどやったように，平均値などのデータの特徴を捉えた数値（統計量）を算出する．そうして得られた統計量に基づき，推測統計学において，その品種のリンゴ全体が「真に持つ」重量の真ん中の値を推測し，またその値の確率的な信頼性の高さを求めることができるのだ．

　これは推測統計学を応用する方法のごく一例に過ぎない．推測は統計学の花形ともいえる分野である．

　残念ながらこの連載では推測統計学が主要なテーマとして話題にのぼることはない．確率モデルや統計的推測といった事項についてさらに知りたいと思われた方は，数学I「データの分析」（本連載）と数学A「場合の数と確率」をマスターした後，数学B「統計的な推測」へと進んでみてほしい（近日公開予定）．

　このように記述統計学はさらなる応用に向けた準備として必要である．だがその限りでなく，データをよく知ろうとする最も基本的な姿勢の体系を学ぶことは，それだけでも我々に実りある洞察を与えてくれるだろう．データの見方が変われば日常の見方も変わるかもしれない！

記述統計学の方法

データ分析の際は，可視化と定量化のアプローチを補完的に行うことが重要である

　データを整理・要約するための方法には大きく分けて次の２つがある：

図やグラフなどによって可視化 (図的表示，visualization) する方法
標本から算出される統計量を用いて定量化（量的表示，quantification）する方法

　データをより良く記述するためには，これらの方法の片方だけで済ますことはできない．両者を互いに補完的に用いることが不可欠である．

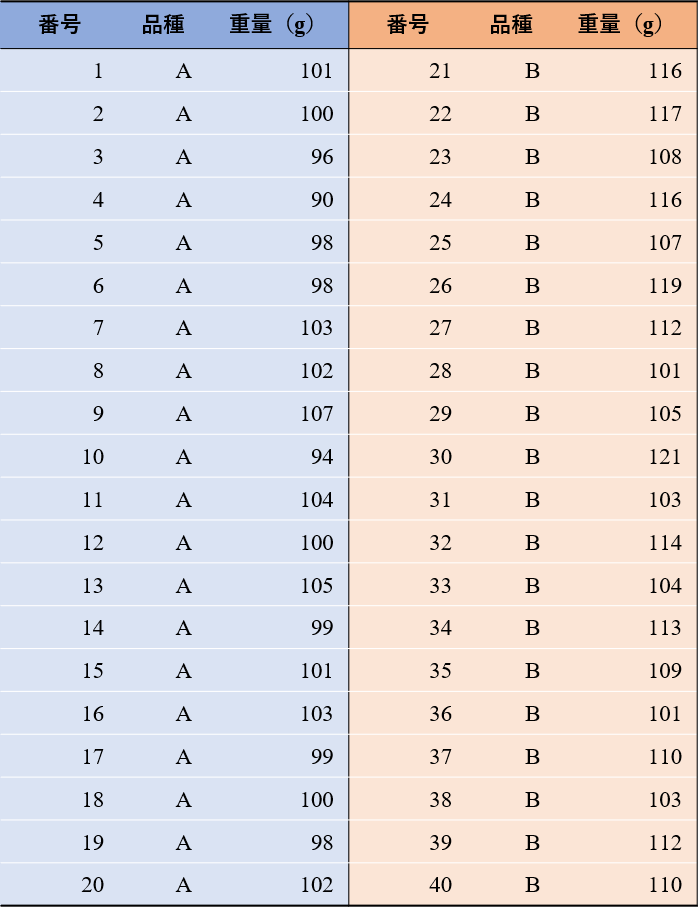
　説明のため，架空のデータを用いて実際に可視化と定量化を行ってみよう．表１は２つのミカン品種についてそれぞれ果実20個の重量を調べた結果だ．これらのデータはどのような性質を持っているだろうか？

表１　ある架空のミカン品種の果実重量データ

可視化のアプローチ

　表１のように統計処理を施す前の測定結果そのもの（生データ，raw data）は，測定値が並んでいるだけなのでデータの性質がイメージしづらい．そこで図１や図２のようにデータを図として可視化して，人間が理解しやすいようにする^注１．

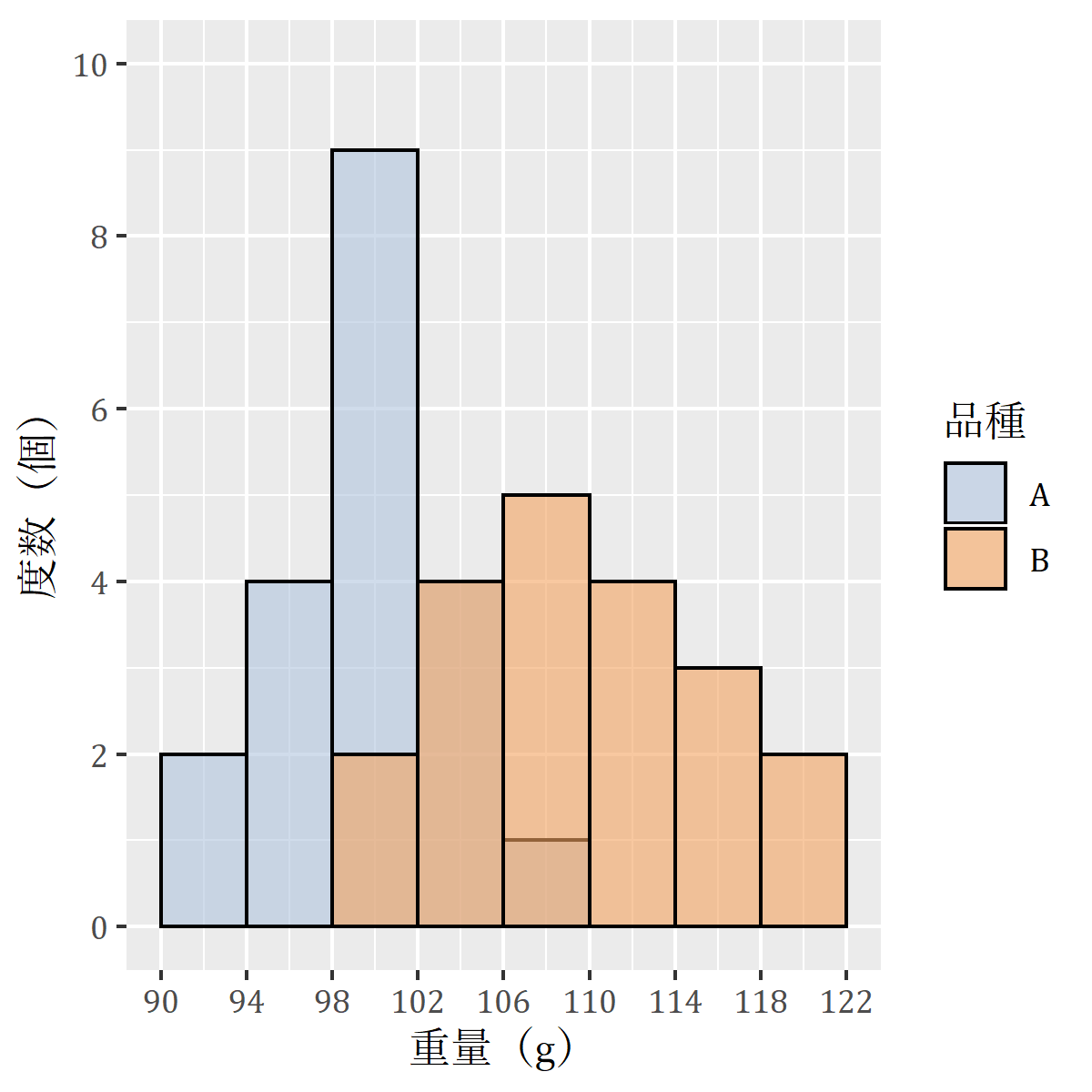
図１ヒストグラムによるミカン重量データの可視化

図２　箱ひげ図によるミカン重量データの可視化

　データを図的に表現する方法はいろいろある．図１はヒストグラム（柱状図，histogram）^注２，図２は箱ひげ図（boxplot）^注３という図的表現だ．ヒストグラムや箱ひげ図の読み取り方や描き方については，のちの記事で詳しく説明する．だから各図についての細かい話はここではあまり気にしなくてよいが，可視化によってデータが持つ大まかな傾向をぐーんとイメージしやすくなることはきっとお分かりいただけるだろう．

　図１や図２から読み取れる，このデータの大まかな傾向とは，たとえば，

品種Bの方が品種Aよりも全体的に実が大ぶりである（つまり，分布の中心がより大きい）
品種Aの方が品種Bよりも実のサイズにばらつきが大きい

などだ．

　またデータを目で見ることは，データの中に異常な値（外れ値，outlier）が含まれていないか確認するためにも重要だ．

注１．本稿に示すヒストグラムと箱ひげ図はプログラミング言語R（バージョン3.5.2）のもとで作成した．特に，‘ggplot2’パッケージ（バージョン3.2.1）を用いて描画したものである．

注２．図１のヒストグラムは，横軸に測定された値の区間，縦軸に各区間に属すデータの個数をとったグラフであり，データの分布を長方形の「柱」の高さで表す．柱の高い区間ほどたくさんのデータが集中していることを意味している．

注３．図２に示した箱ひげ図は，データの中央と散らばり具合を長方形の「箱」によって表現する．箱の区間は，各ミカン品種の20個のデータのうち中央付近の値を持つ10個のデータ（全体の50%のデータ）の範囲を表している．箱の中にある太い横線はちょうど真ん中の値（中央値）である．そして箱に生えた「ひげ」がデータ全体の値の範囲（最大値と最小値の間の区間）を表す．

定量化のアプローチ

　可視化のアプローチは，データの大まかな傾向を掴むのには向いているが，分布どうしが「どれくらい」違うのかを簡潔に表現することが難しい．そこでデータの分布を特徴づけるような数値（統計量，statistic）を算出する，定量化のアプローチが有効だ．データを定量することにより，手軽かつ正確に分布の性質を比較することが可能になる．

　先の2.2.1では表１のデータを可視化したことによって，ミカンの品種Bの方が品種Aよりも概して大ぶりであることが判った．ではその差はどれくらいなのだろうか？各品種データの分布の「真ん中」の値を定量化することで求めてみよう．

　要するに平均値（mean）を比べればよい．品種Aのデータの平均値$\overline{x_{\rm{A}}}$は，次のように20個のミカンの重量を足し合わせ，データの個数で割って求めることができる：

$$\overline{x_{\rm{A}}}=\dfrac{1}{20}(101+100+96+\cdots+102)=100 \, (\rm{g}).$$

同様に品種Bの平均値$\overline{x_{\rm{B}}}$は，

$$\overline{x_{\rm{B}}}=\dfrac{1}{20}(116+117+108+\cdots+110)=110 \, (\rm{g})$$

である．したがって品種Bが品種Aよりも分布の中心が10 gだけ大きいことが判った^注４．

　また図１と図２から，品種Aの方が品種Bよりも実のサイズにばらつきが大きいことが窺われた．これについては，標準偏差（standard deviation）という統計量によって定量して確かめることができる：

$$s_{\rm{A}}=3.67 \, ({\rm{g}}), \quad s_{\rm{B}}=5.73 \, ({\rm{g}}).$$

注４．データの中心を定量化する統計量は平均値のほかにもいろいろある．たとえば最頻値（モード，mode）や中央値（メジアン，median）などもよく用いられる指標だ．最頻値とはデータ内に最も多くの回数出現する値のことで，図１のヒストグラムにおいては山のピークとなる区間の値に相当する：${Mo}_{\rm{A}}=100, \, {Mo}_{\rm{B}}=108 \, (\rm{g})$．また中央値はデータを値の小さいものから順に並べたとき真ん中に来る値のことで，図２の箱ひげ図では太い黒線の値に相当する：${Md}_{\rm{A}}=100, \, {Md}_{\rm{B}}=110 \, (\rm{g})$．表１のような「ある性質」を満たすデータでは，平均値，中央値，および最頻値の値が概ね一致するのだが，品種Bの平均値110と最頻値108のように厳密には等しくならないことがある．詳しくはのちの記事で説明する．