方陣算という文章題をご存じでしょうか?この文章題は,何らかの図形に沿って石やおはじきを並べていき,そのときの図形を構成する石の数や形の移り変わりについて聞いてくる問題を指します。本記事では方陣算について解説していくシリーズの第3本目として,実践に即した攻略法をご紹介していきます。
Contents
基礎編・発展編振り返り!
まずは受験問題を見ていく前に,前々回の基礎編・前回の発展編でどのようなことを学習したか,再確認していきましょう。この2つの記事の中身をきちんと理解できていないと,もしかしたら今回の記事の内容もなかなか頭に入らないでしょう。方陣算についてまだあまり馴染みがない方は,ぜひこれらの記事を一読してみてください。
さてここからは復習に移るのですが,前回と前々回の記事では基礎編・発展編と称し,基本的な4つの図形の形や,その中の石の配置などについてご紹介していきました。4つの図形というのは,中実方陣・中空方陣・三角形・五角形です。もちろんこれ以外の図形も方陣算では出題されますが,基本の形をいくつか覚えておくだけで大分応用が効きます。ぜひ頭に入れておきましょう。

そしてこれらの図形に関して,全体の数や外周の数と1辺あたりの数の関係をそれぞれ見ていきましたね。関係をまとめた式については,長くなってしまうのでそれぞれの記事でご確認していただきたいのですが,全ての図形・全ての関係において大切なことの1つはいくつかのシンプルな図形に分割できないかを考えるということです。例えば真ん中が空いている中空方陣は,大きな四角形から小さな四角形をくり抜いた形のように見ることができます。五角形であれば,中心に存在する1個とそれを取り囲む5つの三角形に分割することが可能です。そしてシンプルな図形に分割することができれば,そこから数についての関係を見出すこともできます。以上のように,方陣算を解くときは最初から数を数え上げていくのではなく,図形を冷静に分析することからスタートしてみると良いでしょう。
問題① シンプルな方陣算に挑戦してみよう!
まずは基本編や発展編でご紹介した,単純な図形における方陣算の答えを計算してみましょう。単純とは言っても引用するのは本番で登場した入試問題です。本番を意識しながら,計算ミス等に注意して進めてみてください。
同じ大きさのご石を正方形の形にすき間なく並べたあと,外側4列を残して中のご石をすべて取り除いたところ,下の図のようになった。並んでいるご石の数が464個であるとき,一番外側に並んでいるご石の数は全部で何個ですか。

(慶應義塾湘南藤沢中等部(2016),一部改題)
解説①
それでは解説に移ります。この問題は典型的な中空方陣に関する問題ですね。そして並んでいる石,つまりは全体の数と一番外側の外周の数が登場していることから,基礎編で学んだことがそっくりそのまま活かすことができそうだとわかります。ここで,前々回の記事でご紹介した中空方陣に関する式をいくつか改めてご紹介しておきます。
1辺に置かれている石の数={(全体の数÷4-列の数×列の数)÷列の数)+(列の数×2)
1辺に置かれている石の数=(外周の石の数+4)÷4
これらの式を見て思い出した方もいるかもしれませんが,この中空方陣というのは全体を隅の部分と隅に挟まれた部分に分割していくと理解しやすい,ということを基礎編ではご説明しましたね。今回の問題ではこの分割を使うことで問題が解けそうです。上の図形において,隅の部分と挟まれた部分とを分けると次のようになります。
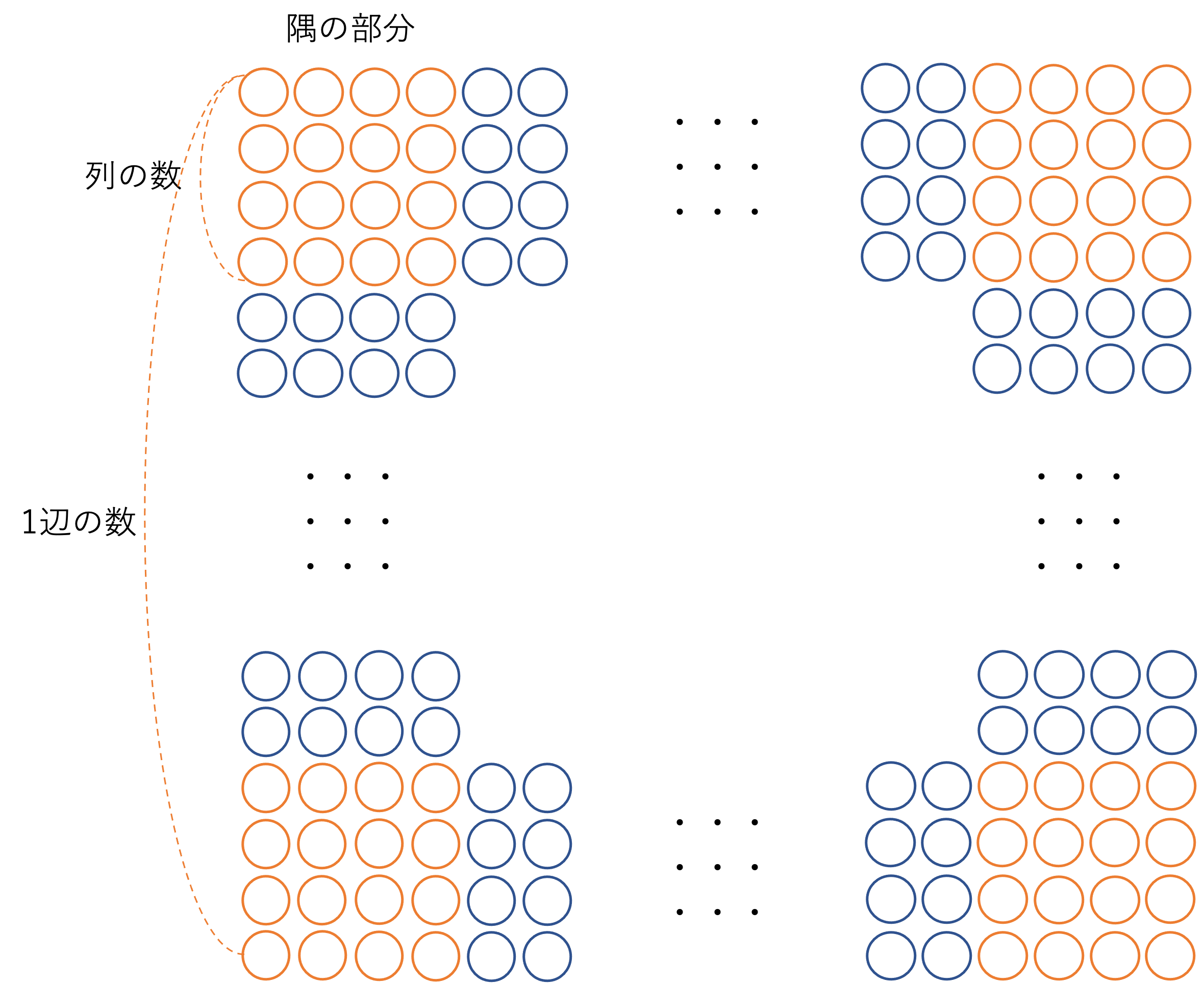
このように,今回登場した中空方陣は4個×4個の隅の部分と,その隅の部分に挟まれた長い部分に分けることができました。そしてこの図からは,列の数が4個だと判断することもできますね。いま問題文で,方陣で使われているご石の全体の数は464個であると示されていることから,上でご紹介した式の1つ目を使うことにより答えが求められそうです。この式が導かれた理由は基礎編にてご紹介するので,「どうしてこの式を使うのだろう」と疑問に思った人は基礎編をご参照ください。さて,このように問題の内容を整理していくと次のような式を作ることができ,計算の結果1辺に置かれているご石の数を計算することができます。
1辺に置かれている石の数={(全体の数÷4-列の数×列の数)÷列の数}+(列の数×2)
1辺に置かれている石の数={(464÷4-4×4)÷4}+(4×2)
1辺に置かれている石の数={(116-16)÷4}+8
1辺に置かれている石の数=25+8=33個
このことから,上の中空方陣の1辺には33個のご石が並べられていることがわかりました。そして今度はこの値を使って外周の数を計算していきましょう。外周の数も上でご紹介した式を使えば計算できそうですね。こちらの式がなぜ成り立つのかも基礎編に書いてありますのでパッとしない人はそちらを見ていただき,ここからは最後の計算に移りましょう。上の式に,先ほど求めた1辺に置かれている石の数を当てはめると次のような計算が行えます。
1辺に置かれている石の数=(外周の石の数+4)÷4
33=(外周の石の数+4)÷4
132=外周の石の数+4
外周の石の数=128個
A.128個
したがって答えは128個となります。このように,やや覚えづらい計算式が多数登場しますが,分割という基本的なテクニックを使えば簡単に問題を解くことができます。また分割の仕方もこれ一つだけではなく,全体は4つの外周がつながった形とも,大きな正方形から小さい正方形を除いた形ともみなすことが可能です。式ももちろん覚えていただきたいですが,演習を通して応用力・柔軟性を養えるといいですね。
問題② 見たことのない形でも柔軟に対応しよう!
続いても分割を使って解いていく方陣の問題です。ただし,今回登場するのは正六角形であるため,自分の力で図形の中に存在する関係性を見つけなければいけません。そのため癖してしまうかもしれませんが,粘り強く頑張っていきましょう。
次の□の中に正しい答えを入れなさい。
右の図のように正六角形状に玉を並べます。一番外側にある玉の数が156個のとき,玉は全部で□個あります。
(大阪星光学院中学校(2018),一部改題)
解説②
それでは解説に移ります。今回の問題では,正六角形を構成するご石の外周の数から全体の数を計算していくというものです。前述したように過去の記事では正六角形を扱わなかったため,どうしていけばいいのかと困惑した人もいたでしょう。しかしこのような見覚えのない問題も,全体の数・外周の数・1辺の数の関係性を見ていくと問題に応えることができます。まずはこの例で登場している図形を使いながら,関係性を具体的な式に表していくことから挑戦していきましょう。
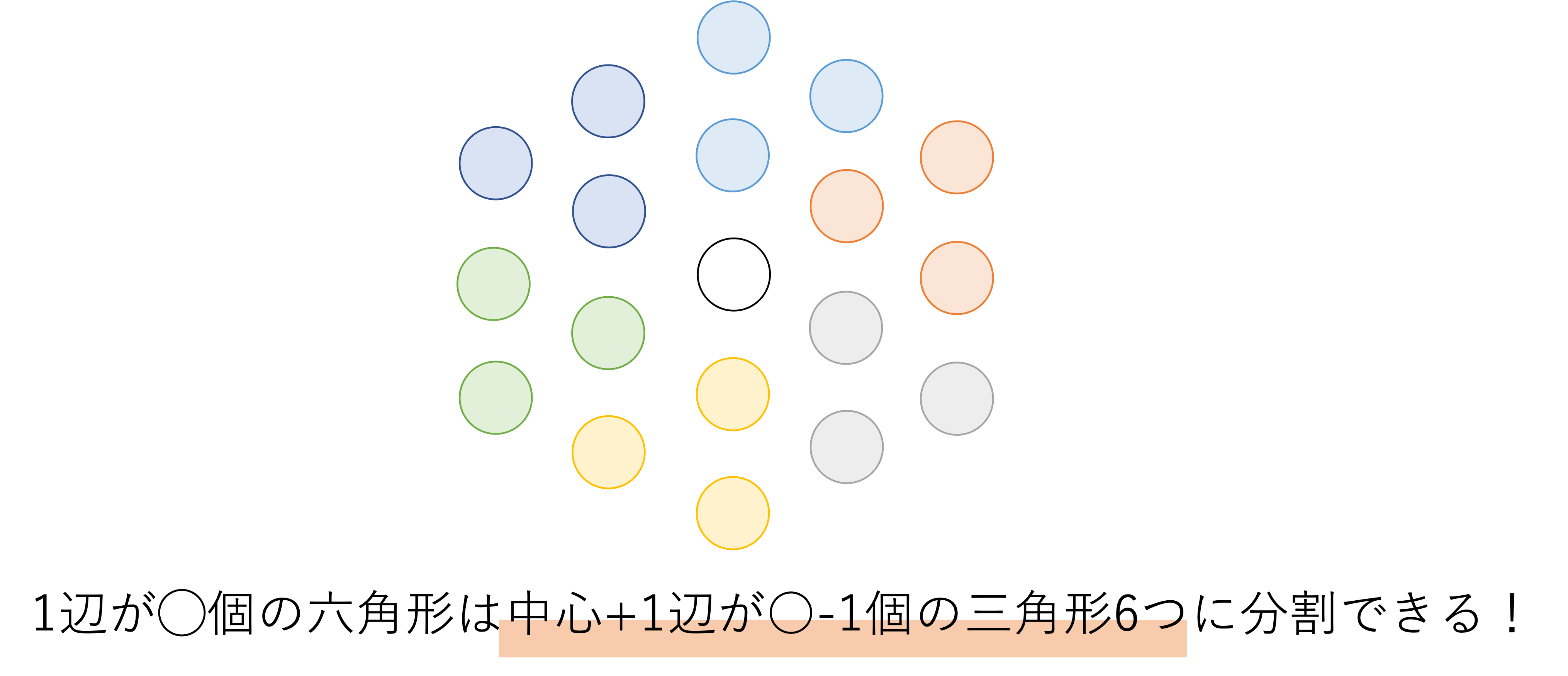
さて全体の数と1辺の数の関係性ですが,まずは発展編で扱った正五角形における全体の数と1辺の数の関係性を思い出してみてください。このとき正五角形は中心の1個の石とそれを囲うように存在する5つの三角形に分割できました。これと同じ要領で正六角形を中心と三角形とに分割していくと,次のように整理することができます。
以上のことからこの六角形の全体の数を計算するためには,中心と三角形5つの数を足し算すればいいとわかります。そして1辺が○個の三角形の全体の数は(○+1)×○÷2という式で計算できることから,この問題では六角形の1辺の数を求めてしまえば,あとは答えとなる全体の数まで計算できそうだと予想できますね。
そして次は1辺の数と外周の数の関係性を見ていきましょう。この2つの関係が分かれば,あとは式に代入していくことで全体の数を計算できます。このように回答の流れの大枠を掴むことはなかなか簡単にはできないかもしれませんが,このスキルが身につくと冷静に問題に対処できるようになります。何が分かればいいのかな,と常日頃から考えていくといいでしょう。さて肝心の外周ですが,こちらも五角形の外周の数を見て行ったときと同じ流れで分割していくことが有効にはたらきます。

このように,六角形の外周は○-1個の部分6つに分解することができます。前回の五角形のときは○-1の部分5つに分解できましたが,図形が何角形であるのかと絡めながら性質や関係を考えていくのは極めて重要です。
そして以上の関係から問題の中身をもう一度考えていきましょう。今回の問題では,六角形の外周が156個のときの全体の個数の合計を求める必要がありました。ここで先ほど見た外周の関係から,六角形の1辺に置かれている石の数は次のように計算できます。
1辺が◯個の六角形の外周の数=(○-1)×6
156=(○-1)×6
○=156÷6-1=27
したがって今回の図形では1辺の数が27個になっていると導けました。ここでさらに上で確認した全体の数と1辺の数の関係性に着目すると,六角形は中心の1個と26段ピラミッド6つに分解できるということも明らかになります。したがって,問題の答えは次のようになります。
1辺が◯個の六角形の全体の数=(○-1)段ピラミッドの全体の数×6+1
1辺が◯個の六角形の全体の数={○×(○-1)÷2}×6+1
1辺が27個の六角形の全体の数={27×(27-1)÷2}×6+1
1辺が27個の六角形の全体の数={27×(27-1)÷2}×6+1=27×13×6+1=2107
A.2107個
以上のように,親しみのない図形や習ったことのない図形でも分割して関係を考えていくことで攻略の糸口が掴めます。遠回りに思うかもしれませんが,焦って答えを考える前に,まずはじっくり図形を眺めてみることがオススメです。
問題③ 石が登場しなくても柔軟に読みとこう!
それでは最後の問題です。この問題では上の2問と違い,ご石が登場しません。そのためパッと見で方陣算かどうかわかりづらいです。しかし中学受験ではこのように,実は〇〇算だけど形がカモフラージュされているから理解しづらい,といった問題も多数出題されます。そのため応用力を養ういい機会だと捉えて挑戦していただけますと幸いです。
図のように数字を規則的に並べていきます。5以下の数字を全て足すといくつになるでしょうか。
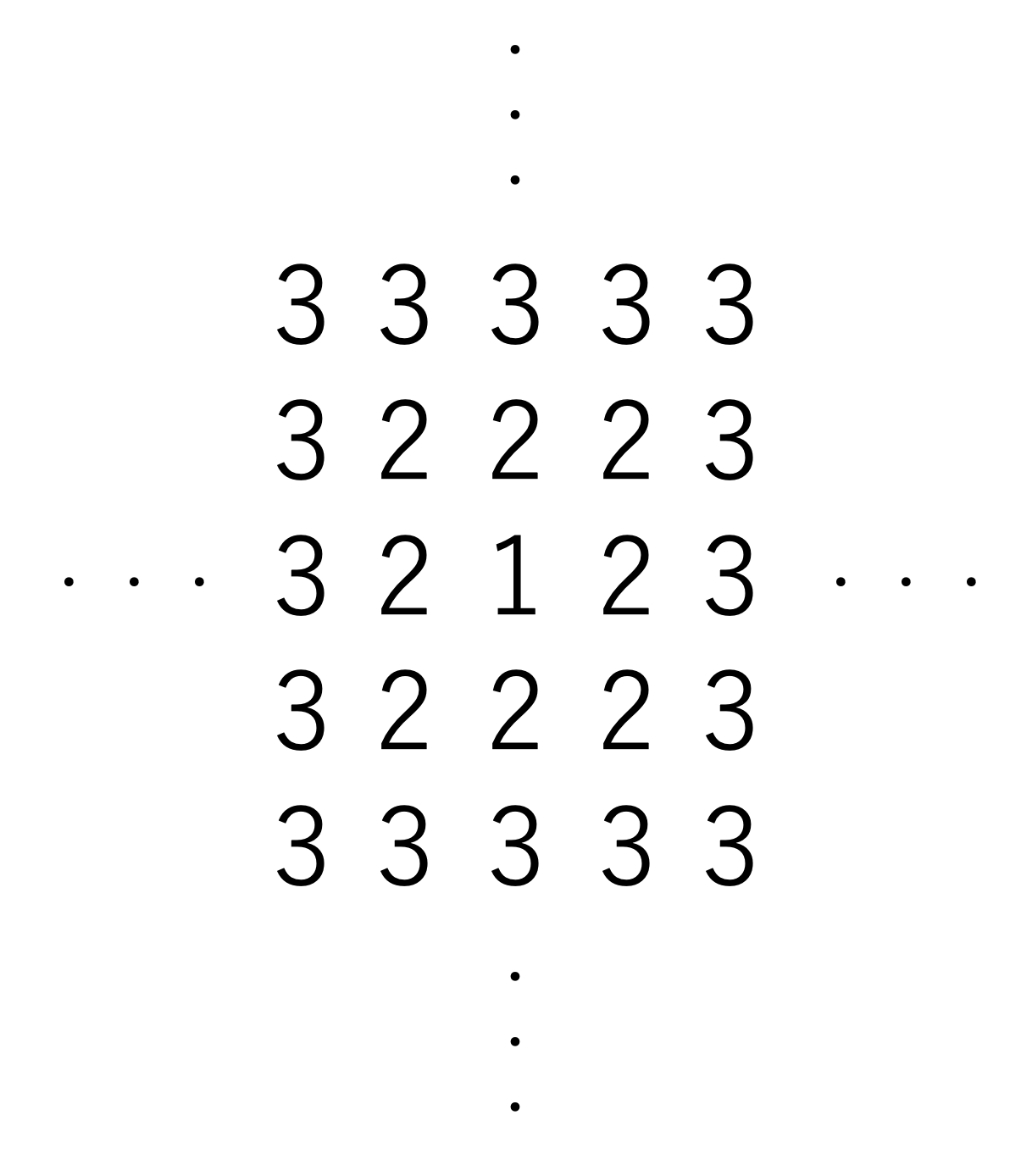
(明治学院中学校(2017),一部改題)
解説③
ここからは最後の問題の解説に移ります。前述したように,数字の羅列を方陣算と考えることが今回の問題では一番難しいところでしょう。一見しただけではわかりづらいですが,よく見れば真ん中に1が存在し,その1を取り囲むように2が,そして2の四角形を囲むように3が,……といった具合で配置されていることがわかります。このような法則性探しが図形を分析する上では極めて重要です。法則性と言っても,「変なところはないかな」といった軽い気持ちで眺めてもらうだけで大抵見出せるようになっています。面白半分でトライしていきましょう。
さて,数字の並びに関する法則性が見えてきたところで,どうやったら答えが求められるかをもう少し深掘りしていきましょう。今回は図形における1から5までの合計を足し算して求めろ,という指示が出ています。つまり次の式にしたがって答えを導いていけばいい,ということが分かります。
1×1の個数+2×2の個数+3×3の個数+3×3の個数+4×4の個数+5×5の個数
ここで上の図から1の個数は1個,2の個数は8個,3の個数は16個だと数えられるので,あとは4の個数と5の個数が分かれば答えを無事導けそうですね。しかし4と5を図形の周りに書いていくことは現実的ではありません。そこで使えるのが方陣算にまつわる関係です。この図形は数字を◯で置き換えると中実方陣だと考えることができますね。そしてある特定の数字の数は,その数字が一番外側にくるときの四角形の外周の数と一致します。例えば図形における2の数に注目すると,2が一番外側にくるとき,1辺に3個の2が並んでいる四角形が出来上がることが分かります。中実方陣において1辺が○個の四角形の外周の数は(○×4)-4個だったので,この○に3を代入して計算すると8個という数字が算出されます。これは先ほど数え上げた2の個数と等しく,このように四角形の形と対照させながら方陣算の式を使っていくと,4の個数も5の個数も導けそうだなと見通しがつきます。
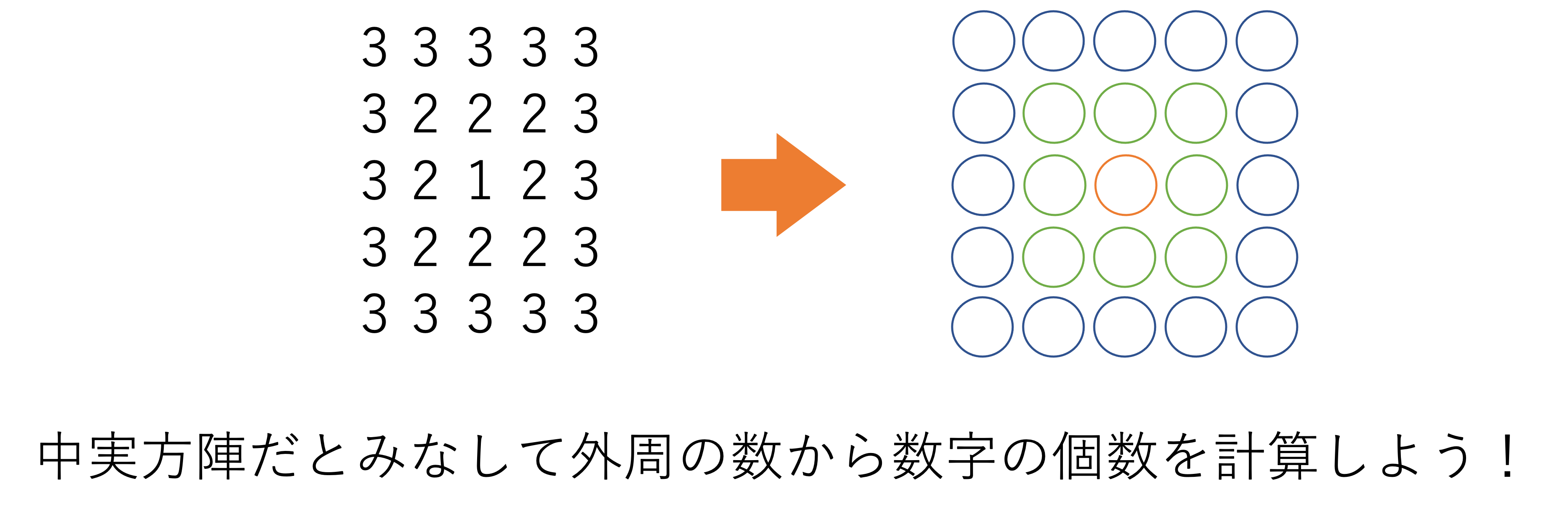
この想定にしたがって4の個数をまずは計算していきましょう。この図形において1が1辺に1個,2は1辺に3個,3は1辺に5個,……と2個ずつ数が増えていっているので,4は1辺に7個ずつ配置されることが分かります。このときの外周の数は(7×4)-4=24だと計算できるので,4は全部で24個存在すると明らかになりました。これと同じ要領で,1辺に9個配置されていると考えられる5の個数についても計算していくと,(9×4)-4=32であることから5は全部で32個存在すると判断できます。
したがって1から5までの全ての個数が求められたところで,あとは上の式に値を代入して合計を計算すると,答えは321となります。
合計=1×1の個数+2×2の個数+3×3の個数+3×3の個数+4×4の個数+5×5の個数
合計=1×1+2×8+3×16+4×24+5×32=321
A.321
終わりに
本記事では方陣算について解説するシリーズの第3本目として,実際に入試で出題された問題を引用しながら,実践的な攻略の方法をお教えしていきました。方陣算は毎回必ず出題される問題ではありませんが,難関校になるにつれて出題頻度は増えていきます。そのため第一志望の中学校を受けるまでには完璧にしておきたい範囲の一つです。よろしければ以下でご紹介するおすすめ記事や参考書籍を活用しながら,さらなる学力向上に励んでいきましょう。



















