今回の記事では方陣算について取り扱う記事の基本編として,中実方陣・中空方陣の特徴を解説していきます。方陣という単語は多くの人にとって馴染みのないものでしょう。そして馴染みがないのは決して言葉だけではなく,その問題の中身も中学受験特有のものなのでほとんどの人が初見ではつまずいてしまいます。そのため本記事を読んで,受験での得点力向上につなげていきましょう。
方陣算の「方陣」とは?
方陣算の解き方を説明していく前に,まず方陣とは何かということに触れておきます。法人とは,簡単に言ってしまえばたてよこにモノを並べていくときの陣形のことを指します。ここで並べられるものとは,囲碁のご石やおはじきのような丸いものが多いです。通常は正方形の陣形を指すことがほとんどですが,問題によっては三角形に配置されたり五角形に配置されたりするため,なかなか手強い範囲の一つです。この範囲では,たとえば次のような問題が出題されます。
49個のおはじきを正方形にしきつめるとき,1辺に使うご石の数は何個になりますか。また,一番外側に並んでいるご石の数は合計で何個になりますか。
240個のご石を使って,真ん中に正方形ができるように3周分ご石を並べました。このとき,一番外側のご石の数はいくつになるでしょうか。
いかがでしょうか。おそらくほとんどの人が,どうやって計算を進めていけばいいのかパッとみただけでは思いつかないことでしょう。しかしこのように難しい方陣算ですが,実はパズルやゲームの要領で楽しみながら解くことができます。今回と次回の記事では問題の攻略の手がかりになる方陣の形について詳しく解説していきます。よろしければ参考にしてみてください。
いろいろな形を覚えよう!
それではここからは方陣の形を覚えていく章の前編として,中実方陣と中空方陣の性質についてお教えしていきます。中実方陣とは先ほど述べた正方形の陣形を指す方陣のうちご石やおはじきが中央まで敷き詰められているものを,中空方陣とはご石やおはじきが中央を空けて囲うように並べられているものを指します。言葉だけでは分かりづらいかと思われるため図を用意しました。
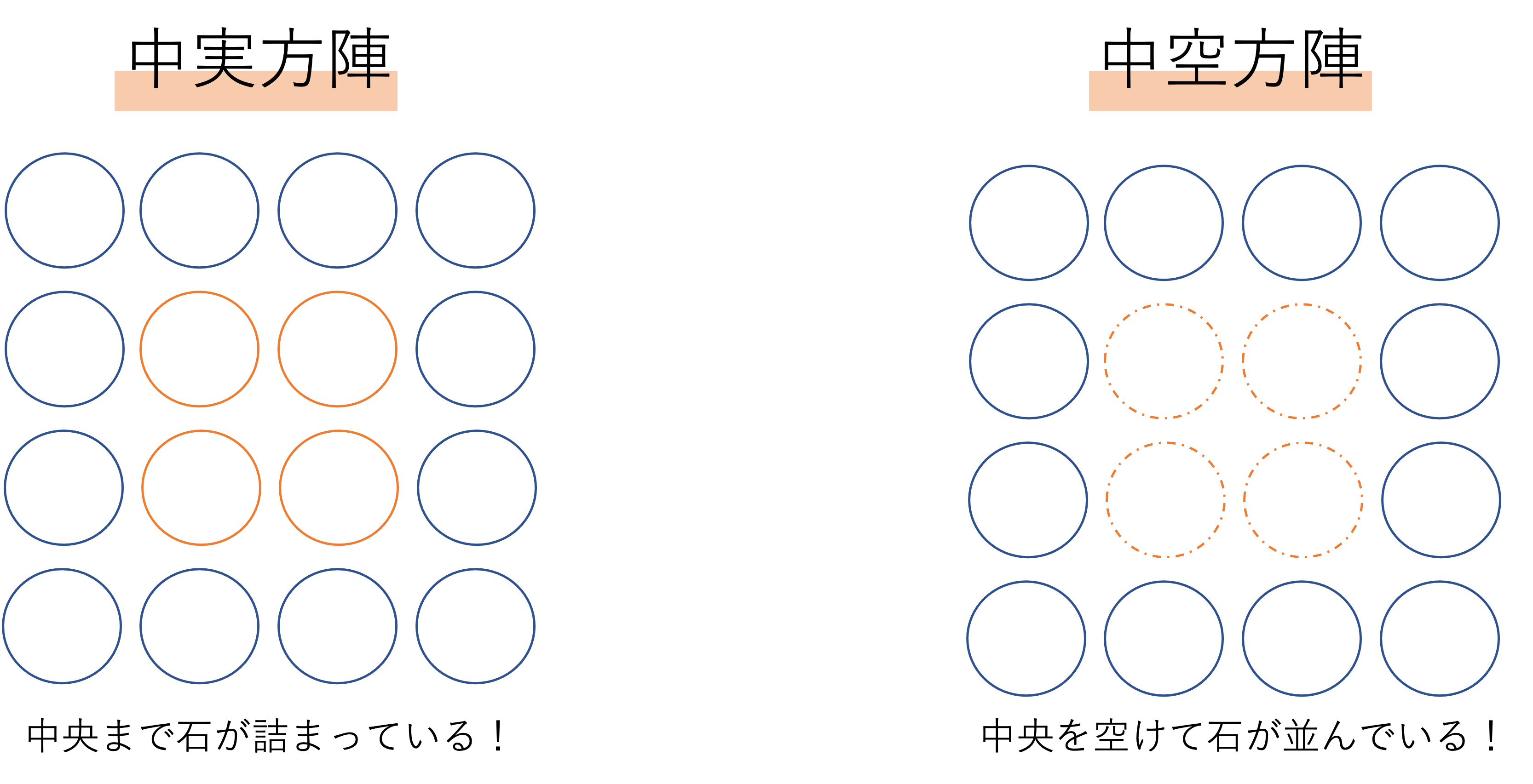
この2つの中実方陣と中空方陣は似たような形をしていますが,全体で使われているご石やおはじきの数が中空方陣の方が少ないという大きな違いがあります。この違いを正確に抑えておかないと方陣算は解きづらいので,まずは今回の記事でこの2つの方陣の性質を覚え切ってしまいましょう。方陣の性質を覚えておく上で大切なことは,それらの形全体を作るのに必要な個数・外周の数・1辺の個数の関係です。したがって以下では中実方陣・中空方陣の順で,それらの要素を確認していきましょう。
中実方陣の性質!
まずは中実方陣の特性から見ていきます。前述したように方陣算では正方形の形が基本となるので,正方形において上でご紹介した3要素がどう関わってくるかを確認していきましょう。初めに1辺の数と全部の数の関係です。敷き詰めた石の全部の数は四角形の面積と同じ要領で,具体的には1辺の数×1辺の数で求めることができます。具体例として,先ほどご紹介した中実方陣を取り上げます。この中実方陣は合計で16個の石が,1辺が4個の正方形を作るように配置されていますね。ここで全体の数は,横に並べられている石の数が縦の列の個数の分だけ配置されていると捉えることができます。そのため1辺の数×1辺の数で計算できるというわけです。
配置されている石全体の数=1辺に置かれている石の数×1辺に置かれている石の数
続いては1辺の数と外周に置かれている石の数の関係です。外周とは方陣の一番端に沿って一周並べられている石のことを指します。ここで注意しておきたいことが,外周は一週分の石,つまり4つの辺に並べられている石のことだから1辺の数×4で計算できる!という間違った考えをしてしまうことです。通常の正方形の周の長さであれば,1辺の長さを4倍することで計算できますが,この方陣算ではそうもいきません。それは被っている石が存在するからです。四隅の石に注目してみましょう。これら4つの石は2つの辺にまたがって存在するため,1辺に置かれている数を純粋に4倍してしまうと四隅を2回カウントしてしまうことになります。したがって正しい公式を覚えておく必要があるわけです。
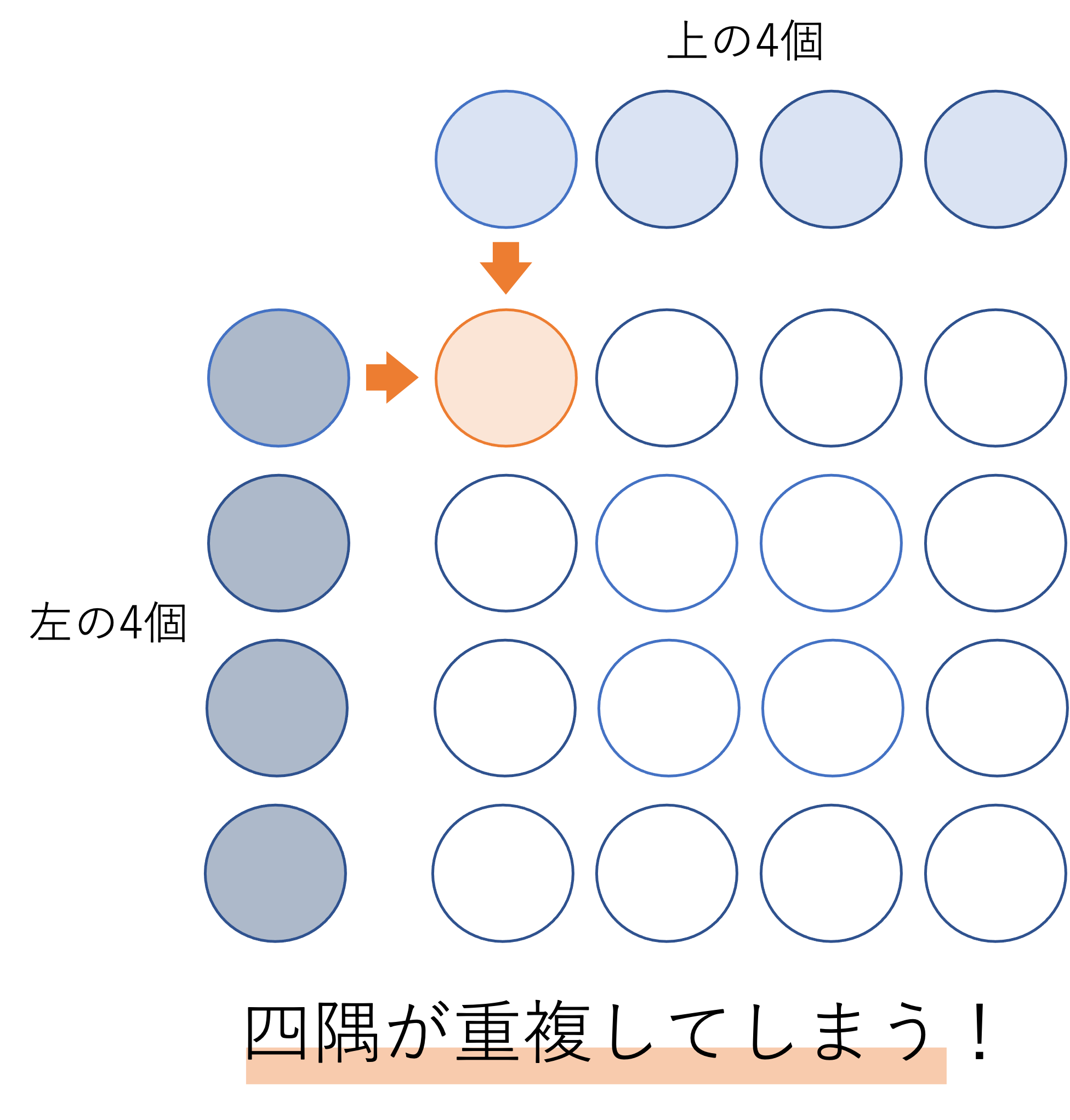
それでは四隅を2回数えないように外周の数を計算するにはどのようにしたらいいのでしょうか。ここで重要になるのが四隅とその間に外周を切り分けていくというものです。以下では先ほどあげた4×4の方陣を使いながら,このテクニックを詳しくお教えしていきます。四隅を2回計算してしまうことを避けるために,まず四隅の数を数えてからそれ以外の数と一緒に足し合わせよう,というのがこのように切り分けた理由です。以上のように切断すると外周に置かれている石の数は,4ヶ所の角に1個ずつ置かれている四隅の石・隅に挟まれた4ヶ所にそれぞれ2個ずつ置かれている石の合計だと考えることができます。
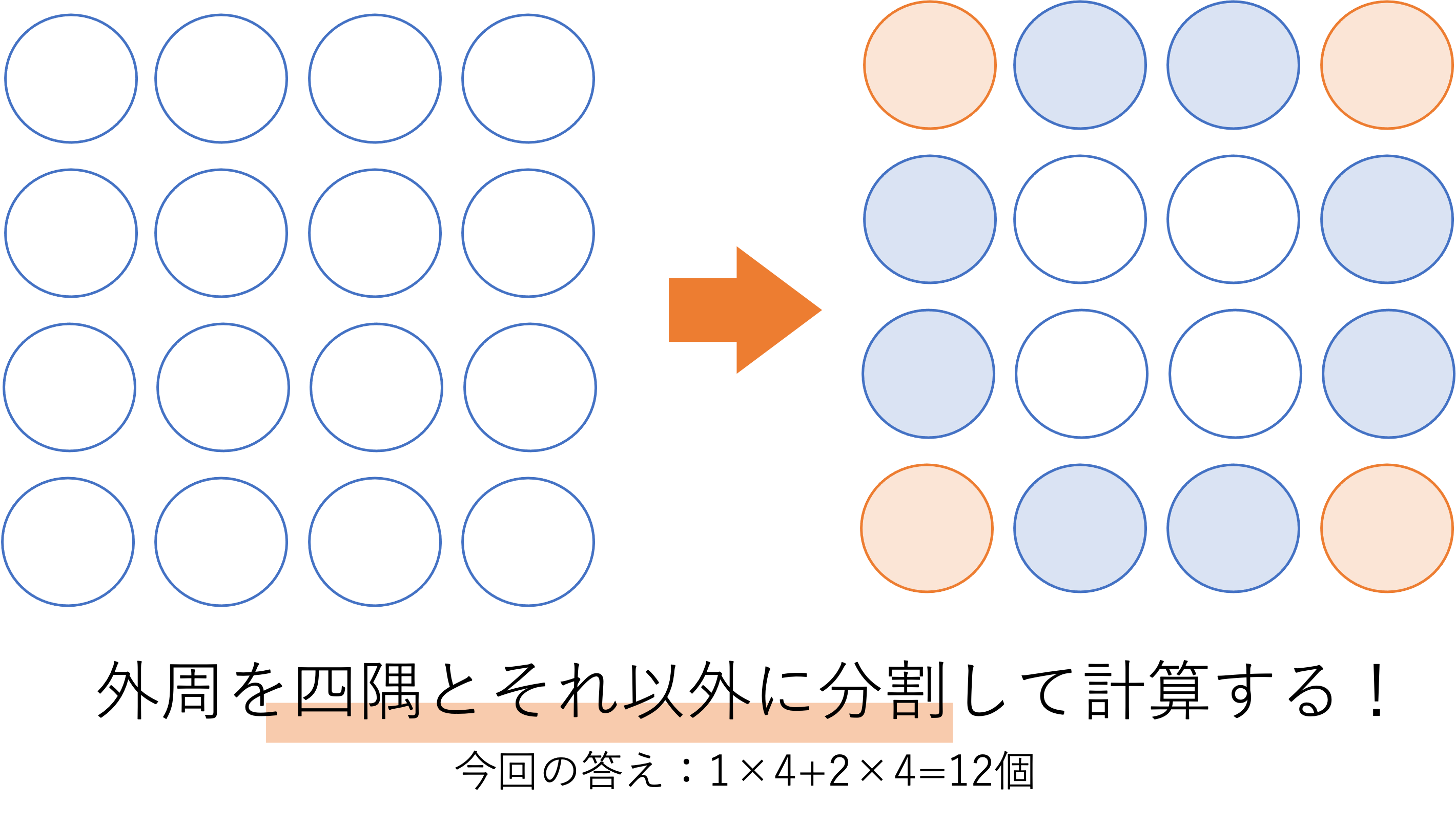
これらを計算式にまとめると次のようになります。
外周の石の数=(1×4)+{(4-2)×4}=12個
そしてこの式を全ての正方形の中実方陣に当てはまるように書き直すと,次のような式が得られるわけです。この外周の数は受験生が最も引っかかりやすい問題ですので,気をつけて頭に入れておきましょう。
外周の石の数=(隅に置かれている石の数×4)+(隅に挟まれた石の数×4)
外周の石の数=4+{(1辺に置かれている石の数-2)×4)
外周の石の数=4+(1辺に置かれている石の数×4)-8
外周の石の数= (1辺に置かれている石の数×4)-4
では中実方陣の最後の特性として,1辺の数の求め方も考えていきましょう。中実方陣の1辺に置かれている石の数は,先ほどご紹介した2つの式を変形することで計算することができます。まず初めに紹介した石全体の数=1辺に置かれている数×1辺に置かれている数の公式を使っていくと,1辺に置かれている石の個数は2回かけると石全体の数と等しくなる数になることが分かります。例えば全体が4個だったら2×2=4であることから1辺には2個,全体が9個だったら3×3=9であることから1辺には3個,……といったように計算することで,1辺の数も求めることができます。
ただこの式だと,4・9・16といった簡単な数以外の計算が行いづらいでしょう。そのため外周の石との関係から考えられる外周の石の数=(1辺に置かれている石の数×4)-4の公式をいじって関係性を覚えていくことをおすすめします。この式を1辺の数について解くと,次のような関係が導かれます。
外周の石の数=(1辺に置かれている石の数×4)-4
1辺に置かれている石の数=(外周の石の数+4)÷4
この式にしたがって辺の数を求めていきましょう。ただし方陣算では全体の数や外周の数が聞かれやすいので,それら2つの指すものや計算方法を覚えてから頭に入れていくといいでしょう。
特殊な中実方陣!
ちなみにこの中実方陣ですが,長方形の場合は少しだけ話が変わってきます。長方形の場合1辺の長さがたてとよこで異なるので,計算の公式の中身が少しズレてくるのです。しかし基本的な考え方は同じです。そこでここでは番外編として長方形の配置のときの攻略法をご紹介します。
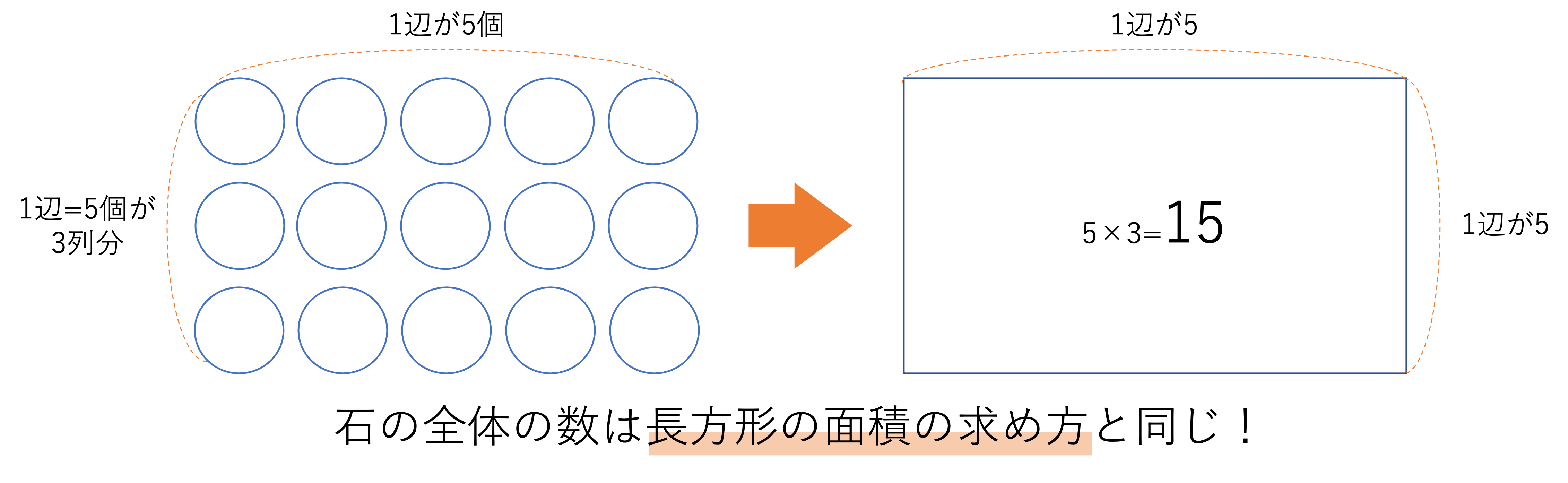
まず全体の数ですが,このときの求め方は面積の考え方と同じです。つまり1辺の長さを2回かけるという式が,全体の数=たて×よこという式に変化します。例えば下の図のような長方形の中実方陣があったとして,ここで使われている石の数は5×3=15個になります。この辺りは面積の公式さえ覚えておけば,問題なく解くことができそうです。
重要なのは外周の数です。こちらも四隅の数が重複してしまうということは変わらないのですが,分割していった結果が正方形のものとは大きく異なるため,慎重に考える必要があります。正方形の場合は四隅とそれ以外という2つのパーツに外周を分割できましたが,先ほど載せた3×5個の中実方陣の場合,四隅とたての余りとよこの余りという3つのパーツに分割することになります。
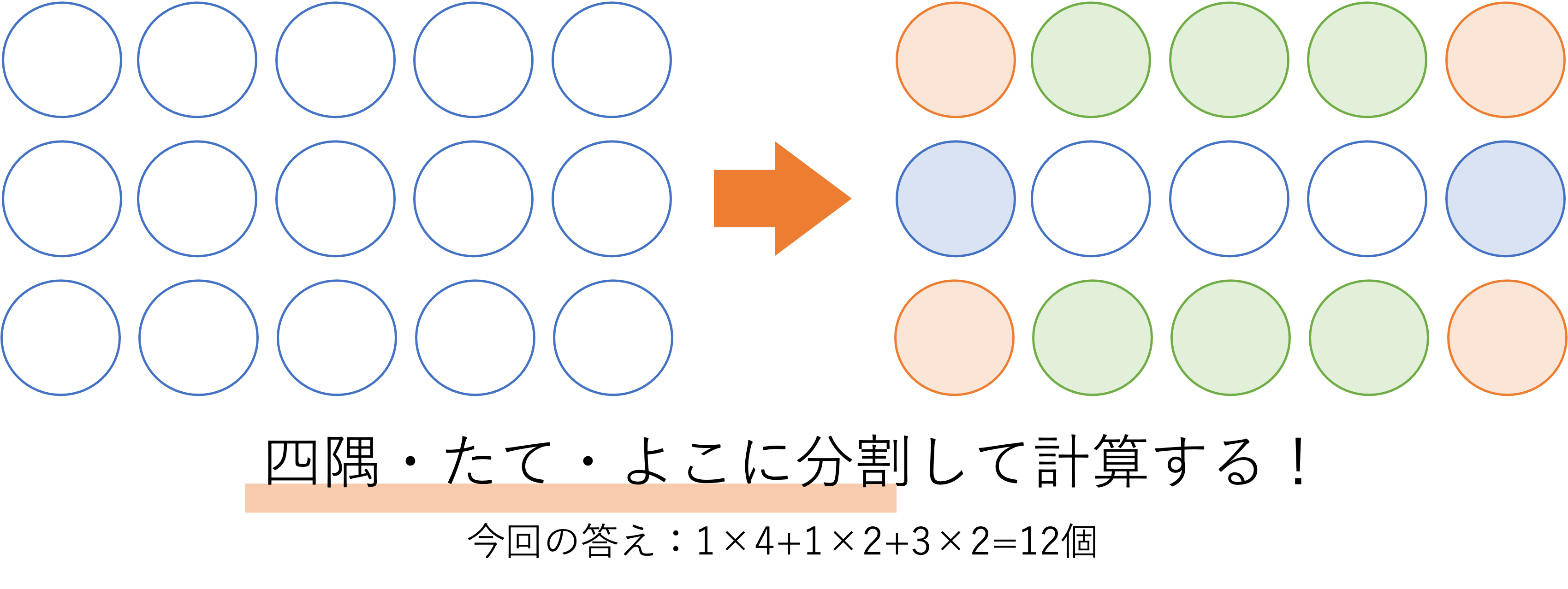
ただ3つのパーツになるということが理解できたのであれば,後はそれらの合計の数を足していくだけなので計算そのものは難なくこなせます。式を立てて計算をすると,答えは次のようになります。
外周に置かれている石の数=四隅の数+2つのたての余り+2つのよこの余り
外周に置かれている石の数=(1×4)+(3-2)×2 +(5-2)×3
外周に置かれている石の数=4+2+6=12個
またたて・よこの数を求めたい場合についても,これら2つの式を変形させることで計算できます。今回は紙面の都合上および変形は正方形のものと大差ないので省略しておきますが,ともかくたてとよこの数が違うだけでいくつもの差が発生してしまいます。その点に気を付けながら覚えていきましょう。
中空方陣の性質!
続いてご紹介するのは中空方陣です。この中空方陣でも全部の石の数・外周の石の数・一辺に置かれている石の数について確認していきましょう。加えて中空方陣ではたてとよこに何列ずつ並べられているかということにも注目する必要があります。その点を意識しながら読み進めていただけますと幸いです。
初めに1辺の石の数と全部の石の数の関係です。中実方陣では一辺の数×一辺の数で計算した全部の石の数ですが,中空方陣では別の式で計算していかなければいけません。というのも,中空方陣では真ん中が空いているからです。真ん中に置かれていない石の数をきちんと省いた上で数を数えないといけないため,答えを導くのに苦戦する人も多いです。ここで重要になってくるのが,先ほどの中実方陣の外周の数でご紹介した分割というテクニックです。中空方陣の全体の石の数を計算するには,外周の数を考えたときのように,4つの隅と隅に挟まれた4箇所の合計8つのパーツに図形を分けてしまうことが重要です。分割した後の様子をお見せすると下のようになります。
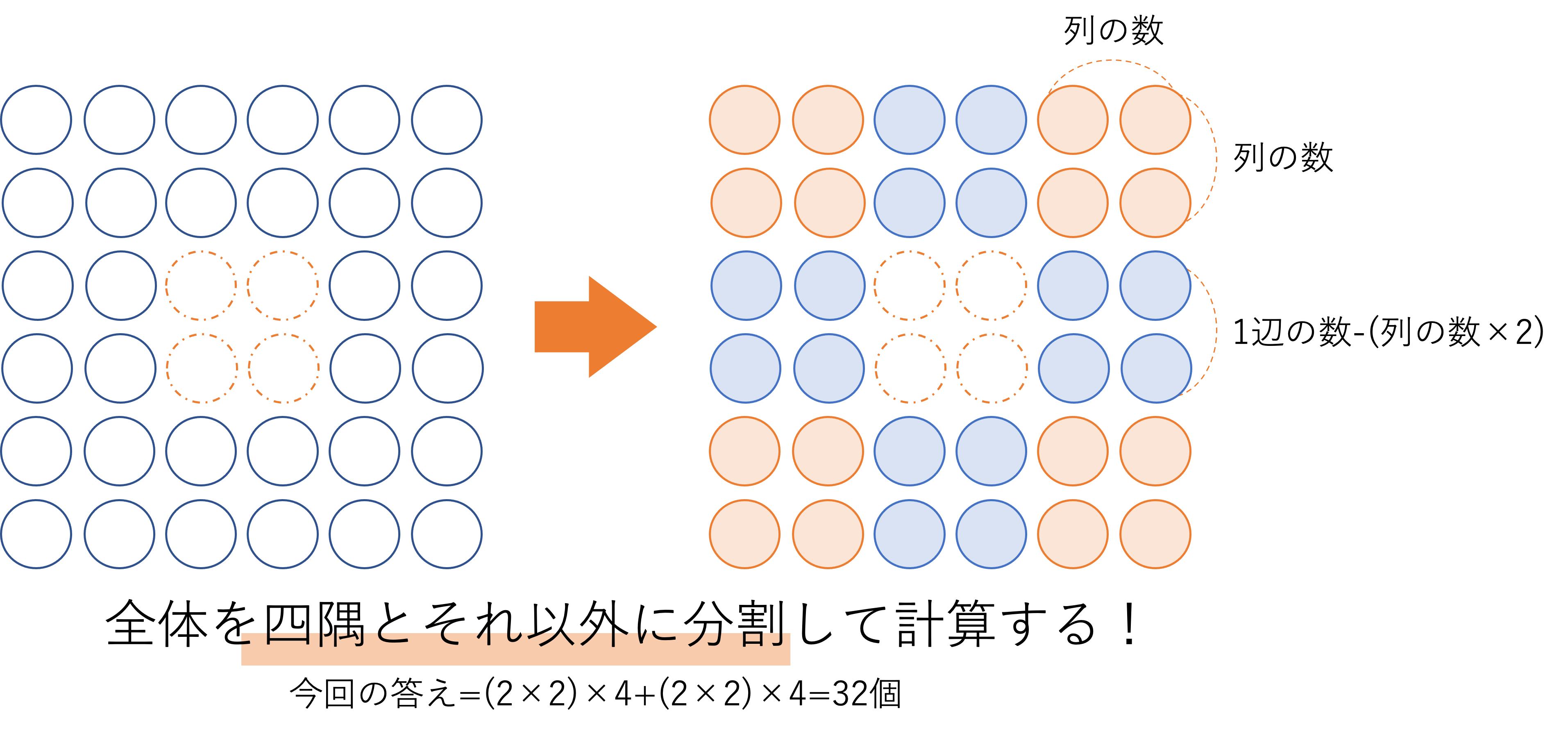
このような8パーツに分割し,それらの合計として全部の数を考えていきましょう。まず四隅に置かれている数を考えると,こちらはたてとよこに並べられた石の列の数をかけ算することで計算できますね。今回は2列ずつなので2×2=4個が四隅にそれぞれ配置されていることになります。そして次に四隅に挟まれた部分に置かれている石の数を計算すると,こちらは1辺に置かれている石から2つの隅の部分と被っている石を除いた数,つまりは1辺の数-列の数×2に列の数をかけ算することで計算できますね。今回だと1辺に6個・たてよこに2列並んでいるので,(6-2×2)×2=4個がそれぞれの部分に置かれているというわけです。そして隅の部分も挟まれた部分も4個ずつ存在しているわけなので、次の式が成り立ちます。これらの計算式はやや分かりづらいので,図を書きながら数え上げてもいいかもしれません。しかし図が大きくなると数え上げるのに時間がかかるので,列の数と辺の数の関係から計算できるようにしておきましょう。
全体の数=(1辺の数-列の数×2)×列の数×4+(列の数×列の数)×4
続いては外周の数ですが,こちらは中実方陣と同じ方法で計算することができます。というのも中実方陣と中空方陣は真ん中に石が詰まっているかいないかが異なるのであって,外を取り囲む一番大きな周は同じだからです。そのため中空方陣の問題でも,四隅とそれ以外とに分けて計算と覚えてしまいましょう。
そしてこのように全体の数・外周の数の求め方が分かったということはそれを使うことで一辺の数も計算できるということです。今回は並べられている列の数というものが登場したため若干複雑になっていますが,基本的にこの列の数は問題の中で指定されるので,関係性をそのまま覚えてしまえば問題ないでしょう。全体の数から一辺の数を計算するには,先ほど見た(1辺の数-列の数×2)×列の数×4+(列の数×列の数)×4を紐解いていけば問題ありません。これを辺の数について解くと,
全体の数=(1辺の数-列の数×2)×列の数×4+(列の数×列の数)×4
1辺の数={(全体の数÷4-列の数×列の数)÷列の数)+(列の数×2)
となるため,この関係に値を代入して計算すればいいですね。なお外周の数から求める場合については,外周の数の求め方が中実方陣と変わらなかったため,こちらも中実方陣と同じように計算することができます。以下の式を頭に入れておきましょう。
1辺に置かれている石の数=(外周の石の数+4)÷4
特殊な中空方陣!
それでは最後に,正方形ではなく長方形の中空方陣が出てきたらどうすればいいかについてご紹介していきます。中実方陣と同じように,中空方陣でも長方形になると計算の仕方が変わってくるので,気をつけて覚えていきましょう。
まず全体の数ですが,このときの求め方は外周の考え方と同じです。つまり全体を四隅・たて・よこの3つのパーツに分割することで,全体でどれくらいの石が配置されているのかを計算することができます。例えば次の図のような中空方陣でも,3種類のパーツに分割することで計算が進められます。なお隅の石が1つ,もしくは正方形になっていないため初めのうちは戸惑うかもしれませんが,テクニックを一度身につけてしまえば計算はうんと簡単になります。まずはこの分割の方法から頭に入れていくといいでしょう。
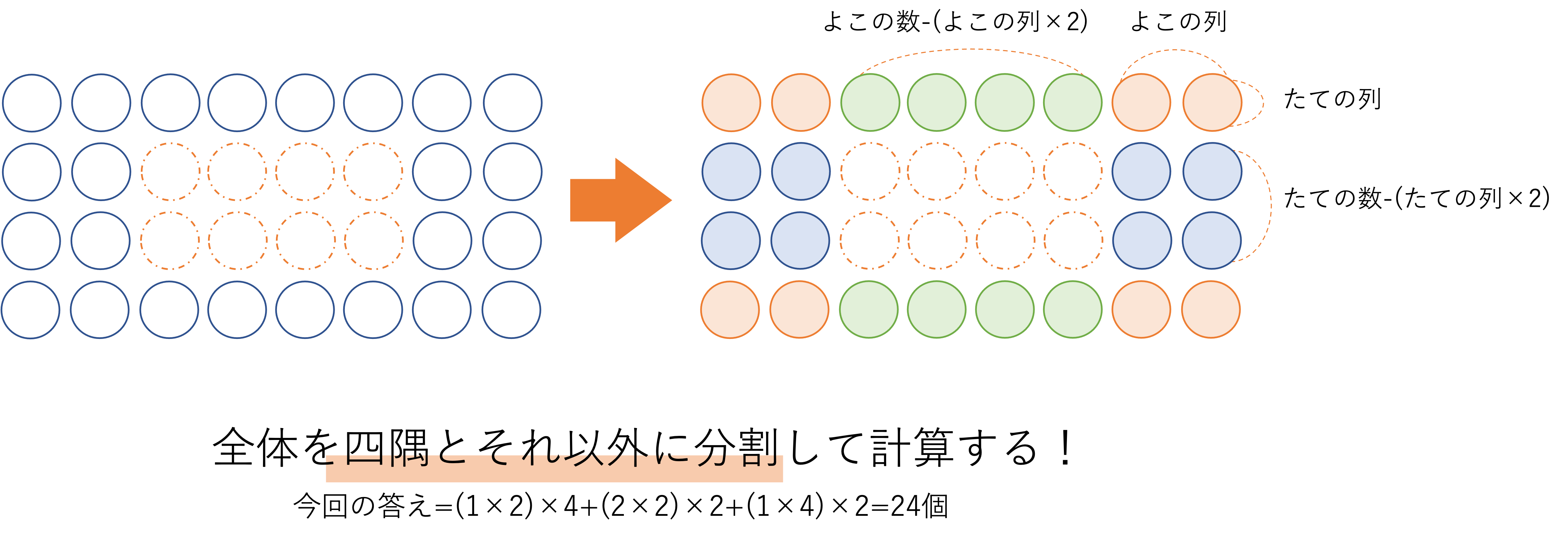
この図から長方形の中空方陣では,全体に置かれている石の数は次のような式で求められると分かります。ぜひ覚えておきましょう。
全体の数=隅の部分×4+たての部分×2+よこの部分×2
隅の数=たての列の数×よこの列の数
たての部分=たての辺の数-(たての列の数×2)
よこの部分=よこの辺の数-(よこの列の数×2)
なお長方形の中空方陣における外周ですが,こちらは先ほどの正方形でご紹介した方法,つまりは分割することで計算ができます。外周に置かれている石の数は中身のあるなしに関わらず一定なので計算式が覚えやすいですね。すんなり頭に入ってくるものから慣れていきましょう。
まとめ……の前に
『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓

さいごに
今回は中空方陣と中実方陣の性質、それぞれの石の求め方について学習しました。あまり馴染みのない分野だと思いますが、特殊なものを含め多くのパターンがあるので、パターン同士の違いに注意しながら学習を進めていってください!
















