本記事では2021年度の中学入試,その中でも特に難関校と呼ばれる偏差値60から偏差値65の中学校で出された問題に焦点を当て,出題のトレンドと対策法をご紹介していきます。このレベル帯を目標とされるお子様も多いかと思われますので,来年受験を控えるご家庭もそれ以降に受験を志すご家庭も,傾向と対策を知っておくと有利に働くでしょう。主な出題傾向は次の3つにまとめられました。ぜひ参考にしてみてください。
Contents
1つ目の出題傾向:工夫が必要な四則演算
まず初めに挙げられる傾向は,工夫して計算する必要のある四則演算です。難関校では,偏差値65以上のチャレンジ校に比べると,計算問題が多くなっています。それは計算の正確さや速さなどの基礎力を図るためでしょうが,中には工夫して計算しないと解けない・工夫することで圧倒的に早く計算できる問題が存在します。例えば今年度は次のような問題が登場していました。
次の□にあてはまる数をそれぞれ求めなさい。
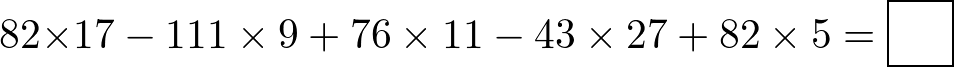
(ラ・サール中学校(2021),一部改題)
次の空欄にあてはまる数を答えなさい。
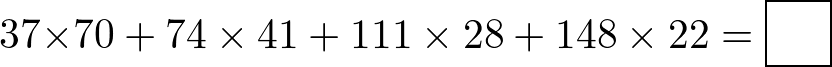
(洛南高等学校付属中学校(2021),一部改題)
どちらも整数の計算であり,じっくりと解けば問題なく正解が導けるお子様の方が多いことでしょう。しかし限られた時間での勝負となる中学入試では,これらの問題を工夫して解かなければなりません。何回も筆算を繰り返している時間は用意されていないのです。そのためこのような式を工夫して変形できるかどうか,が大事になってきます。
工夫がいる計算の対策法は?
ではこのような工夫が必要とされる問題について,どのようにして対処していけばいいのでしょうか。そのために重要なことの一つが,因数分解のテクニックとなります。この知識は中学校で本格的に習うものですが,小学校でも実は計算の工夫についての単元で取り扱っているのです。因数分解とは,端的にいうと次のような式の変形のことを指します。
\(A\times B+A\times C=A\times (B+C)\)
この式は,同じ数をかけて足し算するのであれば,先に足し算をしてから足し算をしてもよいということを指します。このテクニックを使うことで,かけ算の筆算が2回必要だったところが筆算1回で,場合によっては頭の中だけで計算することができるのです。例えば1問目には\(82\times17\)という式と\(82\times5\)という式がありました。この面倒な計算が因数分解を使うことですっきり整理できるのです。
したがって因数分解のテクニックを覚えておくことが重要となります。他にも計算を簡単にする方法はいくつかありますが,おそらく難関校受験において大きく周りと差をつけるのが因数分解を知っているか知らないかになります。ぜひこの技術を身につけておきたいところです。
2つ目の出題傾向:平面図形からの出題
2つ目の出題のトレンドは,平面図形からの出題です。先日ご紹介した【チャレンジ校】の記事では空間図形が出題の傾向だ,とご説明したのですが。難関校では平面図形の面積や角度を求める問題が多く出題されていました。例えば次のような2つの問題が挙げられます。
図のような,正六角形ABCDEFがあり,その面積は10\(cm^{2}\)です。BG=EHでGI:IC=2:3です。次の問いに答えなさい。(式や考え方も答えなさい。)
(1)四角形ABDFの面積を求めなさい。(2)三角形BGIの面積を求めなさい。
(3)三角形IDJの面積を求めなさい。
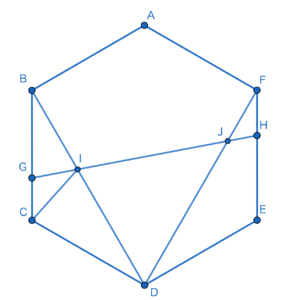
(武蔵中学校(2021),一部改題)
下の図において,CEの⻑さは□cm,⻑方形ABCDの面積は\(□cm^{2}\)です。このとき,図の×では半円が⻑方形の辺にぴったりくっついています。
(洛南高等学校付属中学校(2021),一部改題)
これらの問題は問題集などでよく見られるものですが,それでも慣れている人と慣れていない人とでは大きな差が出てきます。このような問題ではいかにはやく回答の糸口を見つけ出せるか,が重要です。中学受験に臨むにあたって対策は欠かせないでしょう。
平面図形の対策法は?
ではこのような平面図形の問題にはどのように対策していけばいいのでしょうか。平面図形では,まず図形の性質をしっかりと把握しておくことが重要です。例えば⻑方形であれば対になる辺の⻑さが等しいということや,ひし形であれば対角線が直角に交わるなど,図形の性質をもとに図にどんどん情報を書き込むことが大事になってきます。
そして覚えた図形の性質をもとに,図形同士の足し引きを考えることが問題を解く上で大切になります。難関校で出題されるのは単なる正方形やおうぎ形の問題ではなく,高さ・底辺がわかりづらいなど簡単には解けないものばかりです。そのため様々な視点から図形を眺める必要があります。
例えば1問目の四角形ABDFの面積であれば,一目見るだけで直角に交わる辺が無いことがわかると思います。今回は六角形の面積から2つの小さな三角形の面積を引くことで面積を求められる,と見通しが立てられるのですが,このような視点は一朝一夕で身につくものではありません。平面図形に対するこのような知識・発想力を養うためには応用レベルの問題を反復練習していくことが大事です。先ほどの四則演算は出題のパターンがある程度決まっていますが,平面図形に関しては無限の問題が存在します。そのため知らない問題にどんどん挑戦して,柔軟に対応する力を身につけていきましょう。
3つ目の出題傾向:速さに関する問題の出題
最後にご紹介するのは速さに関する問題です。先日投稿した【チャレンジ校】の記事でも速さに関する問題がトレンドだ,とご紹介しました。旅人算・流水算といった速さに関わる問題は中学受験の大きなトレンドと言っても過言ではないでしょう。
そのなかでも難関校で出題されていた問題は,チャレンジ校のものと比べて条件が短くてわかりやすいもの,すなわち解く速さと正確性が問われるものが多い印象でした。例えば次のような2つの問題が挙げられます。
ある列車は,⻑さが400mのトンネルに入り始めてからで終わるまでに36秒かかります。また,この列車が1.5倍の速さで走ると,⻑さ800mの鉄橋を渡り始めてから渡り終わるまでに40秒かかります。この列車の⻑さは何mですか。
(浦和明の星中学校(2021),一部改題)
図のような道路があり,PQ間は600m,QR間は320m,RS間は800mです。

太郎君はPからSへ向かって,次郎君はSからPに向かって,同時に出発しました。太郎君がSに着いたとき,次郎君はPまであと344mのところにいました。なお,2人が歩く速さはそれぞれ一定です。
(1)2人が歩く速さの比を求めなさい。
別の日に,RからQへ向かって一定の速さで動く歩道ができました。太郎君はPからSへ向かって,次郎君はSからPへ向かって,同時に出発しました。すると,2人はRですれちがいました。ただし,QR間は動く歩道を歩くものとします。
(2)太郎君が歩く速さは,動く歩道が動く速さの何倍ですか。
太郎君がSについてから2分42秒後に,次郎君はPに着きました。
(3)太郎君が歩く速さは毎分何mですか。
(洛星中学校(2021),一部改題)
どれもみ・は・じの情報がしっかりとわかりやすく,それでいて登場する数字も100,1.5といった比較的キリがいいものが多いですね。したがってこれらの問題は基本的な計算手順に則っていけば解くことができるのですが,解答のためにどのような対策をとっておけばいいのでしょうか。
速さの問題の対策法は?
前述したように,このような難関校で出題される問題は意外にも基本的な計算手順に沿って解いていけるものが多いです。それはこの速さの問題はどこまでも難しくすることができるからです。【チャレンジ校】の記事を見ていただけるとわかるのですが,応用レベルの問題では登場する人物が多かったり,グラフが登場したり,何通りにも条件が分岐することがほとんどです。
しかしいくら標準的な難易度とはいえ,本番の緊張した状況では解きにくく感じてしまうかもしれません。そのため対策が必須となります。対策方法としては,一般的なレベルの問題を解いて,問題のパターンを覚えておくことが効果的でしょう。このような文章や条件が出てきたらこのように解く,というパターンが染み付いていれば,身についた流れに沿って情報を整理して計算をすることができます。
そして次に大事なのが,今解いている問題が何算なのかの確認です。パターンだけを覚えていても,今解いているのが何算なのかの把握が間違っていたら折角覚えたパターンが意味をなしません。こういう言葉があったら旅人算で,こういう言葉があったら流水算だ,といった具合で問題の種類と頻出する言葉をリンクさせて初めてパターンに沿って解くことができます。対策のため演習を重ねるときには,ぜひこのような意識を心掛けていただければと思います。
まとめ
今回は偏差値55から偏差値65までの中学校で2021年度に出題された問題を眺め,その出題の特徴や傾向をまとめ,対策法をご紹介していきました。傾向と対策をまとめると次のようになります。
- 傾向その1:工夫が必要な四則演算→因数分解などのテクニックを覚えよう!
- 傾向その2:平面図形からの出題→図形の性質を覚え,大局的な視点を身につけよう!
- 傾向その3:速さに関わる問題→問題が何算かを考え,パターンに沿って解こう!
傾向を知っておくと効率良く受験のための勉強を進めることができます。もちろん全ての範囲の基礎から応用までを完璧に仕上げることが理想ですが,なかなか難しいと思いますので,よろしければ本記事でご紹介した特徴をふまえて学習プランを立てていただければと思います。本記事が今後の勉強のお役になれば幸いです。















