今回は数ある文章題の中から,過不足算と差集め算という問題をピックアップしてご紹介していきます。このような文章題は試験のうち大問1,小問集合で出されがちです。そのため早く正確に解くために,たくさん演習を積んでおく必要があります。基礎から紹介していいますので,「聞いたこともない…」という人はこの記事を読んで対策していきましょう!
Contents
「過不足算」「差集め算」は同じもの!
過不足算=問題文の特徴/差集め算=計算過程の特徴
はじめに過不足算とは・差集め算とは何か,についてお話ししていきます。
中学入試で登場する文章題は,名前から内容を推測しづらいものが多く,初めて触れる人は「過不足算・差集め算」と言われてもピンとこない方が多いと思います。またこの2つはセットで取り上げられることが多く,頭の中でこんがらがっている人も多いのではないでしょうか。
結論から言ってしまうと,過不足算と差集め算とは全く同じものであり,どちらも「あるものをいくつか用意したときの差から全体の数を計算する」という問題を指します。扱うテキストなどによって言い方が違うだけで,中身は全く同じです。強いて言えば,おそらくこのような用語の違いが生まれているのは,注目している部分が異なるからだと推測されます。
過不足という単語は,「過」剰と「不足」とが組み合わさってできたものです。過剰とはあるものの数が想定より多く存在している状態を,不足とはあるものの数が想定より少なく存在している状態を指します。つまり過不足算とは,これらの過剰と不足ということが関わってくる問題なのです。問題文で過不足の条件が指定されるという文章の特徴に注目したものが過不足算だといえます。
他方差集めという単語は「差を集める」という漢字で構成されています。これは問題の解き方の話です。詳しくは次の章で解説しますが,この「過不足算・差集め算」の答えは,問題で登場する過剰している量と不足している量を合わせる,つまりは差を集めることにより求めることができます。このことから差集め算とは解答の過程に注目した用語といえます。
以上の理由から呼び名が異なるのではないだろうか,と私は考えますが,ここで一番覚えて欲しいのは,前述したように2つのものが同じ内容を指すということです。このことを知らないと過不足算・差集め算を別々に取り組んで時間を無駄にしてしまった…!なんてことにつながりかねないので,ぜひ覚えておいてください。
基本的な出題パターン!
では早速ここからは過不足算・差集め算の出題パターンに注目していきます。
例えば次のような問題が過不足算・差集め算に当てはまることになります。過不足算・差集め算といえばこれ!というお決まりの文章ですので,下の例題に似ている問題が出てきたら,今回の記事で学んだことが使えそう!と覚えてしまってもいいでしょう。
みかんがいくつかあります。これらを家族でひとり2個ずつ分けるとみかんは5個あまり,3個ずつ配るとみかんは1個足りません。このとき,みかんはいくつあるでしょう?
このようにあるものの全体の数がわからず,分ける・配るという作業を伴う文章題が,過不足算・差集め算と呼ばれるものです。問題によっては過剰・不足の2つの場合が書かれているのではなく,過剰のケースが2つ書かれていたり,逆に不足のケースが2つ書かれていたりすることもありますが,基本的な解き方は変わりません。
配る・分けるといった言葉・差といった単語が出てきたら,「これは過不足算・差集め算かもしれない」と疑ってみると良いでしょう。
問題の攻略法をご紹介!
では以下では上の章で紹介した例題を使いながら,過不足算・差集め算の解き方をご紹介していきます。改めて先ほどの例題を記載しておきます。よろしければ解説を読む前に,自分の力だけで解けるかどうか,試してみてください。
みかんがいくつかあります。これらを家族でひとり2個ずつ分けるとみかんは5個あまり,3個ずつ配るとみかんは1個足りません。このとき,みかんはいくつあるでしょう?
いかがでしょうか?解けた人も解けなかった人もいるとは思います。ただ大事なのはいま解けるかどうかではなく,受験当日までに解けるよう勉強しておくことなので,解けた人は改めて答えの確認をしながら,解けなかった人は答えの求め方を覚えながら,読み進めてもらえますと幸いです。
ポイント① 情報をまとめよう!
まずこのような問題に出会ったら,情報を1つの図にまとめることが大事です。この整理する・まとめるということは全ての文章題で通じることですので改めて説明するまでもないかもしれませんが,やはり文章だとわかりづらいことも多いかと思われますので,日頃から徹底しておきましょう。
今回の例題で登場する情報といえば,みかんの全体の個数・家族の人数,そして何個ずつ配るか・そのときいくつ差が出るか,ですね。これらを簡潔にまとめると下の図のようになります。みかんの絵まで書く必要はありませんが,このような形式で図を書く習慣がついていると良いかと思われます。
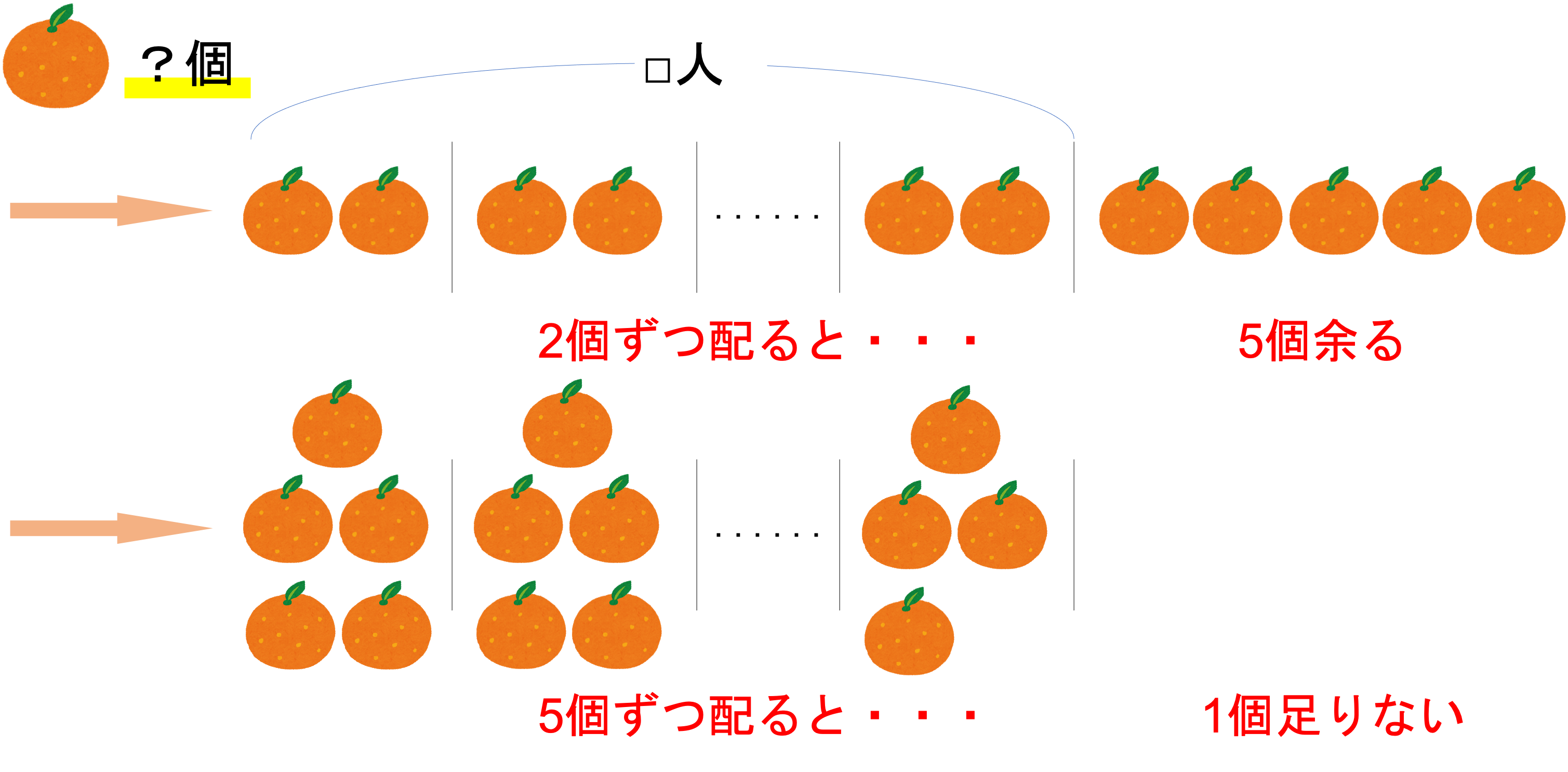
ポイント② 全体の差・1人あたりの差を考える!
では情報をまとめられたところで,ここからが過不足算・差集め算特有の計算を行なっていきましょう。今回答えとして求めるものはみかんの全体の個数でした。全体の個数は次の計算式で求められます。
全体の個数=\(2\times□+5=5\times□-1\)
いまはこの□,つまり人数がわからないので全体の個数は計算できませんが,人数さえ求められれば問題の答えも計算できそうだ,と予測が立てられます。したがって人数に着目して計算を進めることが大事です。
この人数を求める上で重要なのが,みかんの1人分の差とみかんの全体の差になります。1人分の差とは一人頭に配られるみかんの差のことを意味し,全体の差とは全員に分けていったときに余る個数の差を意味します。
今回配られるみかんの量の差は,2個ずつの場合と5個ずつの場合が挙げられていたので,1人について3個の差があることがわかります。そして全体で見ると,2個ずつ分けると5個余る・5個ずつ分けると1個足りないので,全体では6個の差があることがわかります。
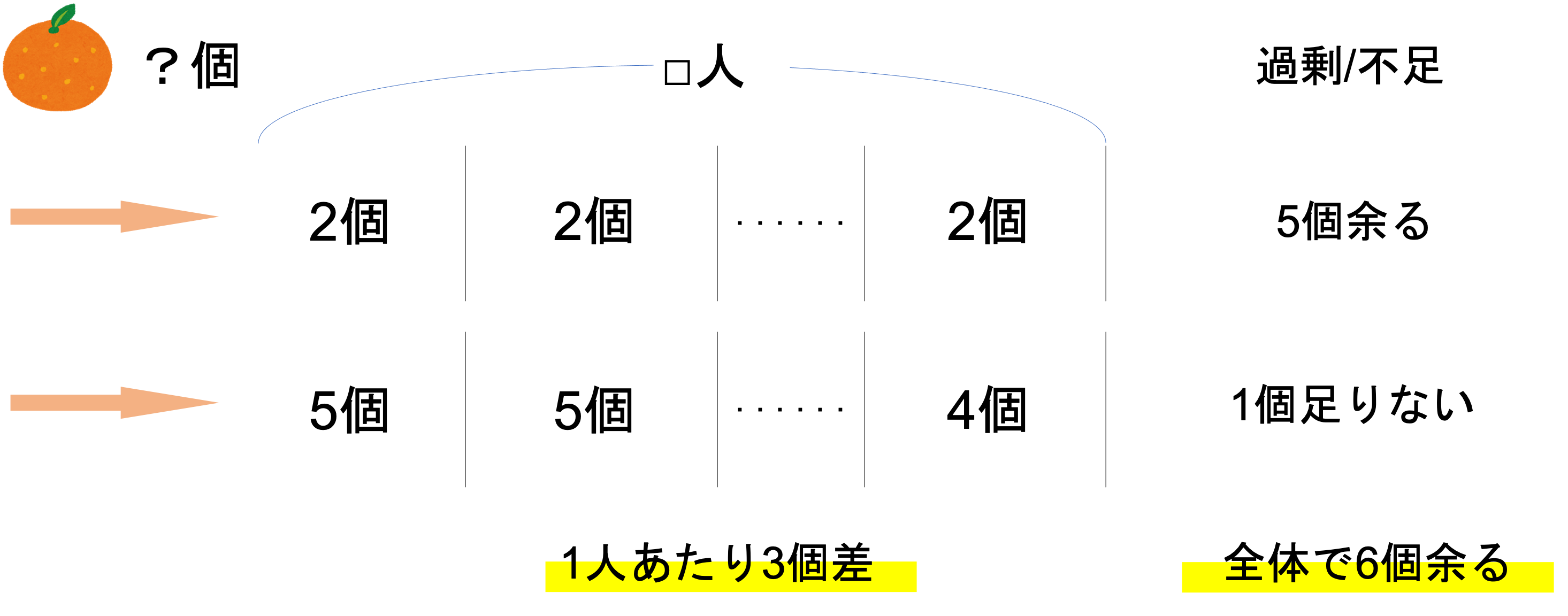
ここで全体の差は,1人あたりの差をすべて足した数に等しくなります。今回は1人当たりの差が3個とわかっているので,それらを人数分集めたものが全体での差である6個になるわけです。
1人あたりの差\(\times\)人数=全体の差
\(3\times\)□(人)=6
したがって上の計算式が成り立ちます。これを解くと□=2と分かりますので,家族は2人ということが導かれました。このことから前述の式に人数を当てはめることで,全体の個数が計算できますね。
\(2\times2+5=9\)
このことからみかんは9個だと分かります。
A.9個
一応5個配ったら1個足りないという式の方にも人数をあてはめて,答えを確かめておきましょう。
\(5\times2-1=9\)
したがってみかんの個数は9個で間違っていないと分かります。過不足算・差集め算では2つ以上の式が立てられることがほとんどですので,確かめ算の習慣をつけておくことも忘れないでください。
攻略法のまとめ!
以上で過不足算・差集め算の解き方の紹介は終わりとなります。改めて解く上でのコツを箇条書きにしてまとめておきます。
- 個数・差などに注目して情報を図に整理する。
- 全体の差・1人あたりの差に注目して計算を進める。
はじめのうちはこのような解き方に苦戦するかもしれませんが,たくさん問題を解いているうちに慣れていくかと思います。今回の記事を読むだけではなく,演習を積み重ねていくことが大切です。
練習問題を解いてみよう!
それでは過不足算・差集め算の基本的な攻略法を理解していただけたところで,最後に1問似たような問題を解いて攻略法に慣れていきましょう。先ほどの例題とそこまで難易度が変わらないよう作問しましたので,よろしければいまの自分の力で解けるかどうか試してみてください。
1本50円の消しゴムと,1本150円のシャーペンを同じ本数ずつ買ったら,消しゴムの代金とボールペンの代金の差が500円になりました。消しゴムとシャーペンを何本ずつ買いましたか。
練習問題の解説!
それではここからは問題の解説に移ります。整理する→全体/個々の差に注目する,という手順を踏むことはこの問題でも変わらないので,上でご紹介した攻略法に沿って解いていくことにします。まずは今回登場した消しゴム・シャーペンについての値段と個数の関係をまとめていきましょう。
このとき,例題ではあとから個々の差や全体の差を考えていきましたが,慣れていったら一度にこれらの情報もまとめて抑えてしまうといいでしょう。今回の問題の条件をまとめると下の図のようになります。
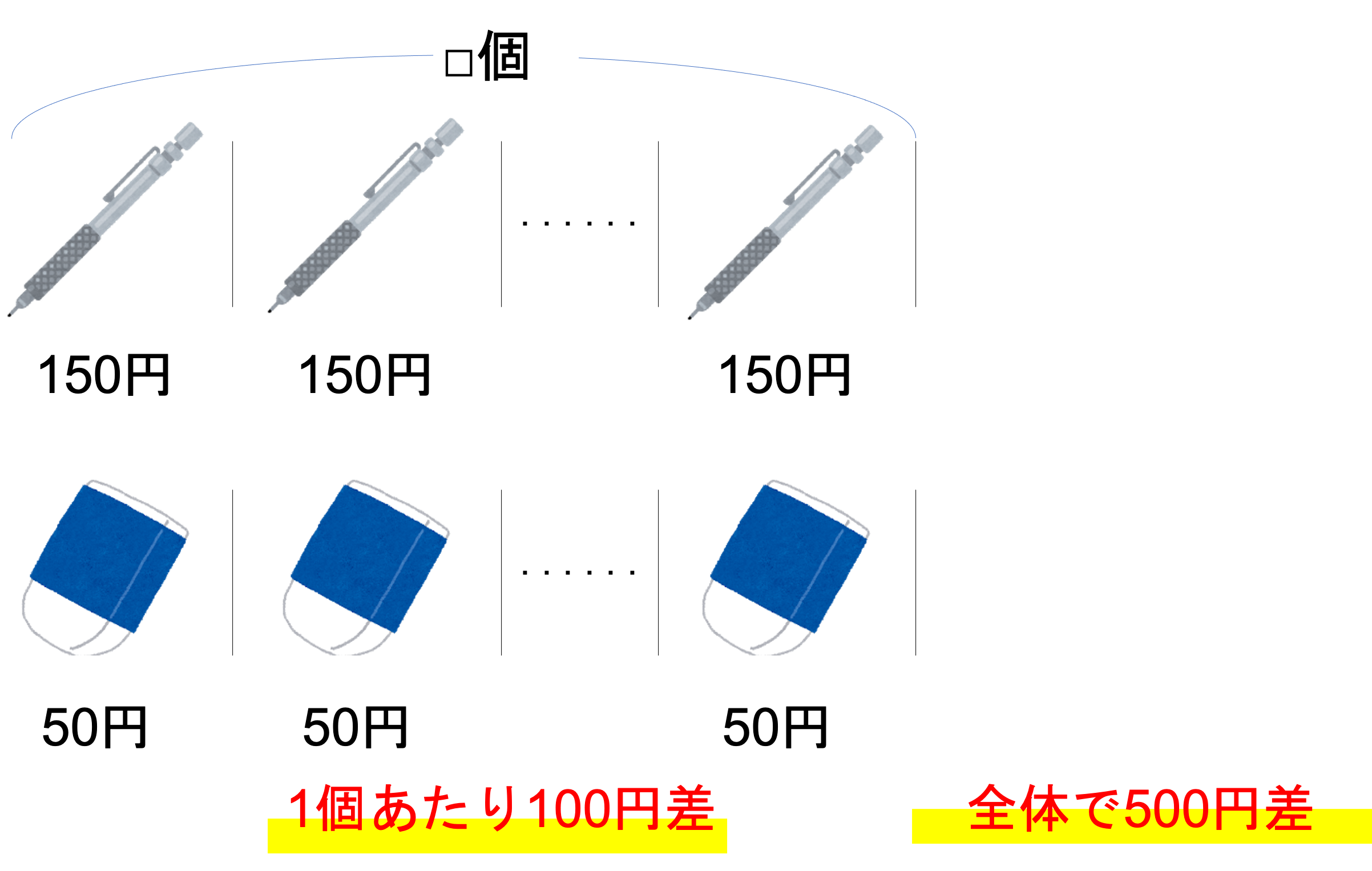
では続いて個々の差と全体の差に注目して計算を進めていきます。今回の問題を読むと,シャーペンが150円・消しゴムが50円で売られていることがわかります。そのためシャーペンの代金と消しゴムの代金は100円離れている,つまり1個あたりの差が100円だと判断できます。また全体の差については,問題文中で「消しゴムの代金とボールペンの代金の差が500円になりました」と言われているので,500円離れていると言えます。
そして1個あたりの差が買う個数分集まると全体の差になるという関係から,
1個あたりの差\(\times\)人数=全体の差
という式が成り立つことは,例題でも触れたかと思います。今回の問題でもこの式に則ると,
100\(\times\)□=500
という関係が導かれます。これを解くと□=5,つまり消しゴムとシャープペンを5個ずつ買った,ということが求められました。
A.5個
念のため確かめ算も行いましょう。消しゴム5個の値段とシャーペン5個の値段を求めると,消しゴムが250円・シャーペンが750円となります。この差は500円ですので,個数は5個で間違いないと確かめられました。この確かめ算も,基礎・演習に関わらず毎回行う習慣をつけておくといいでしょう。
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

おわりに
今回は過不足算・差集め算についての基礎的な知識と攻略法をご紹介していきました。ここでお話ししたのはほんの一部の問題に過ぎませんが,このような初歩的な問題を積み重ねることで受験に適応する算数の力が育ちます。ぜひこの記事で学んだことを生かす練習を積んでいただければと思います。本記事が今後の学習の手助けになれば幸いです。
(ライター:大舘)

















