今回の記事では,水の深さと体積に関する記事の第3本目として,複雑な容器に関する問題の解き方をご紹介していきます。この問題は図の体積・グラフの2つの大きなポイントに対する理解が必要とされるため,苦手とする人も非常に多いです。そのため早い段階からの対策が不可欠です。よろしければ本記事をお読みいただくことで,対策を進めていきましょう。
Contents
「複雑な容器問題」とは?
今回取り上げていくのは,数ある水の体積と高さに関する問題の中の一つである複雑な容器問題です。この分野の問題では,複雑な形をした水そうの中に水を入れていくというシチュエーションが登場し,水を入れていく時間と水面の高さを比べながら,どういう風に水が溜まっていく様子が変化していくかが問われる問題です。よく出題される形が次のようなものです。典型的な図形は直方体がくっついたような形をとっているため,立体の切断などのテクニックが必要となってきます。またそのほかにも,仕切りが設けられている場合も存在するため,冒頭でも説明したように図形に対する知識だけでなく水の溜まり方に関する想像力も必要とされます。この能力はなかなか鍛えられるものではないですが,普段の遊びやゲームの中で考える機会を少しずつ増やしていくことで,徐々に養成することができます。よろしければおすすめ記事などをご参考にしていただけますと幸いです。
例題を解いてみよう!
それではここからは例題を解きながら,問題を解く上で必要となるポイントについて整理していきます。今回の問題はやや複雑な問題に見えますが,実は至って標準的な難易度の問題です。立体とグラフの両方が登場することに頭を抱える人もいるかもしれませんが,難しく感じているのは誰しもに当てはまることなので,今後解けるようになれば問題ないという意識で眺めていただけると幸いです。
図1のような直方体を2つ合わせた形の水そうがあります。図2は,空の状態から,はじめ毎分25L(リットル)の割合で水を注ぎ,深さが20cmになったときからは毎分40Lにしていっぱいになるまで水槽に水を入れたときの時間と水の深さの関係を表しています。アに入る数を求めなさい。
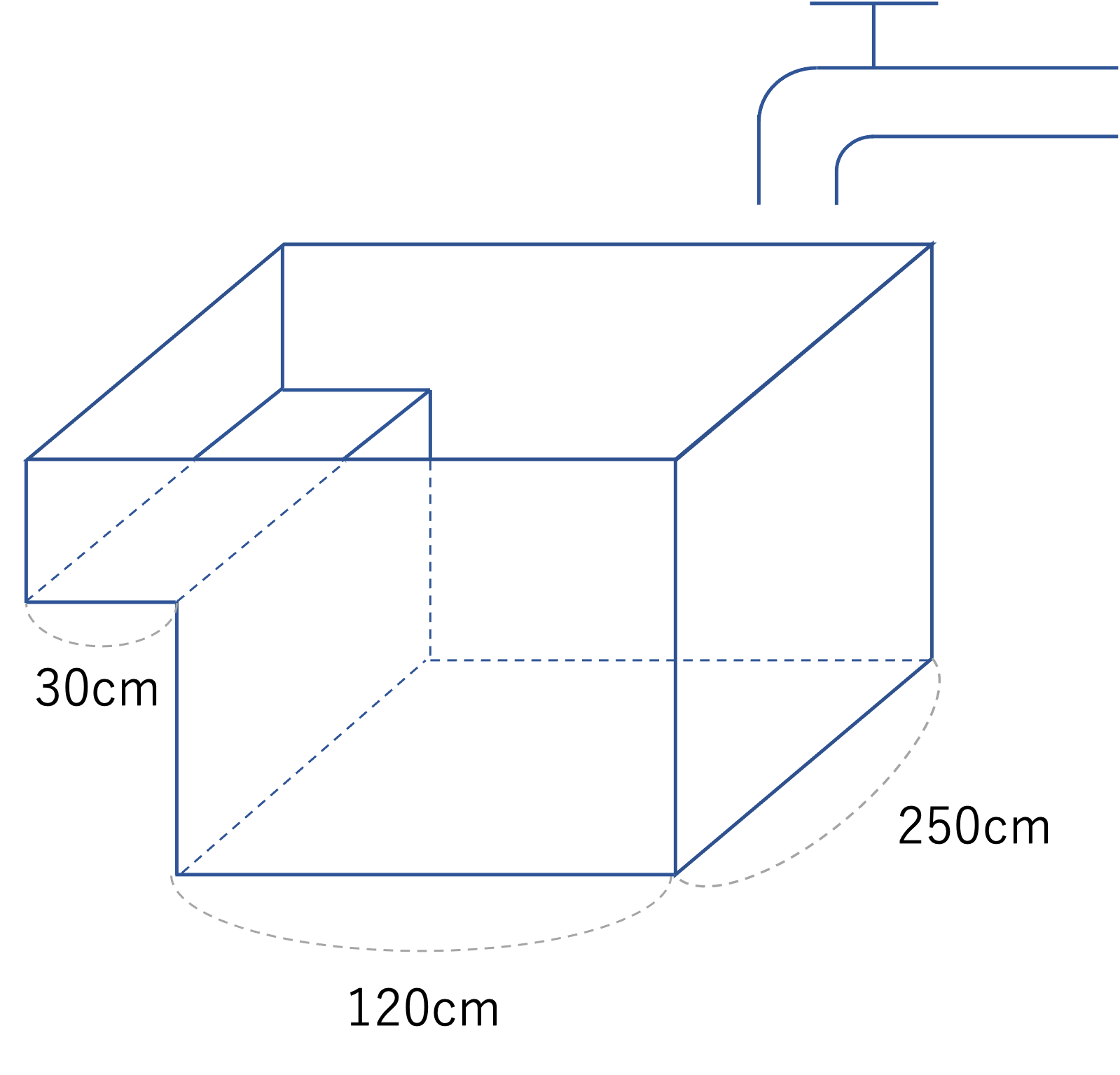

(武蔵中学校(2013),一部改題)
解説①まずは問題文の整理!
それではここからはこの問題を使いながら,複雑な容器問題を解くコツをご紹介していきます。まず肝心なのが問題文の中身を整理するということです。今回は複雑な容器問題として問題文をご紹介していますが,受験に実際出題されるときは「これは複雑な容器問題からの出題です」と明言されるわけではありません。そのため,いま自分が解かなければいけないのはどの範囲からの出題かを理解し,テクニックを思い出すために整理の手順が必要になるわけです。
今回注目しておきたいのは,グラフと立体の登場です。複雑な容器問題であるかどうかはこの2点の有無で判断することができます。そしてその次に大事なのが,水を入れていく速さをはじめとした一連の数値への注目です。今回ははじめに毎分25L・その後毎分40Lと1回だけ水を入れる速さが変化しています。問題文が長くなればなるほどこれらの要素は見落としてしまいやすいので,明らかになっている情報でも自分の言葉や書き方でまとめていくことが大事です。意識しておきましょう。
解説②グラフの転換点に注目しよう!
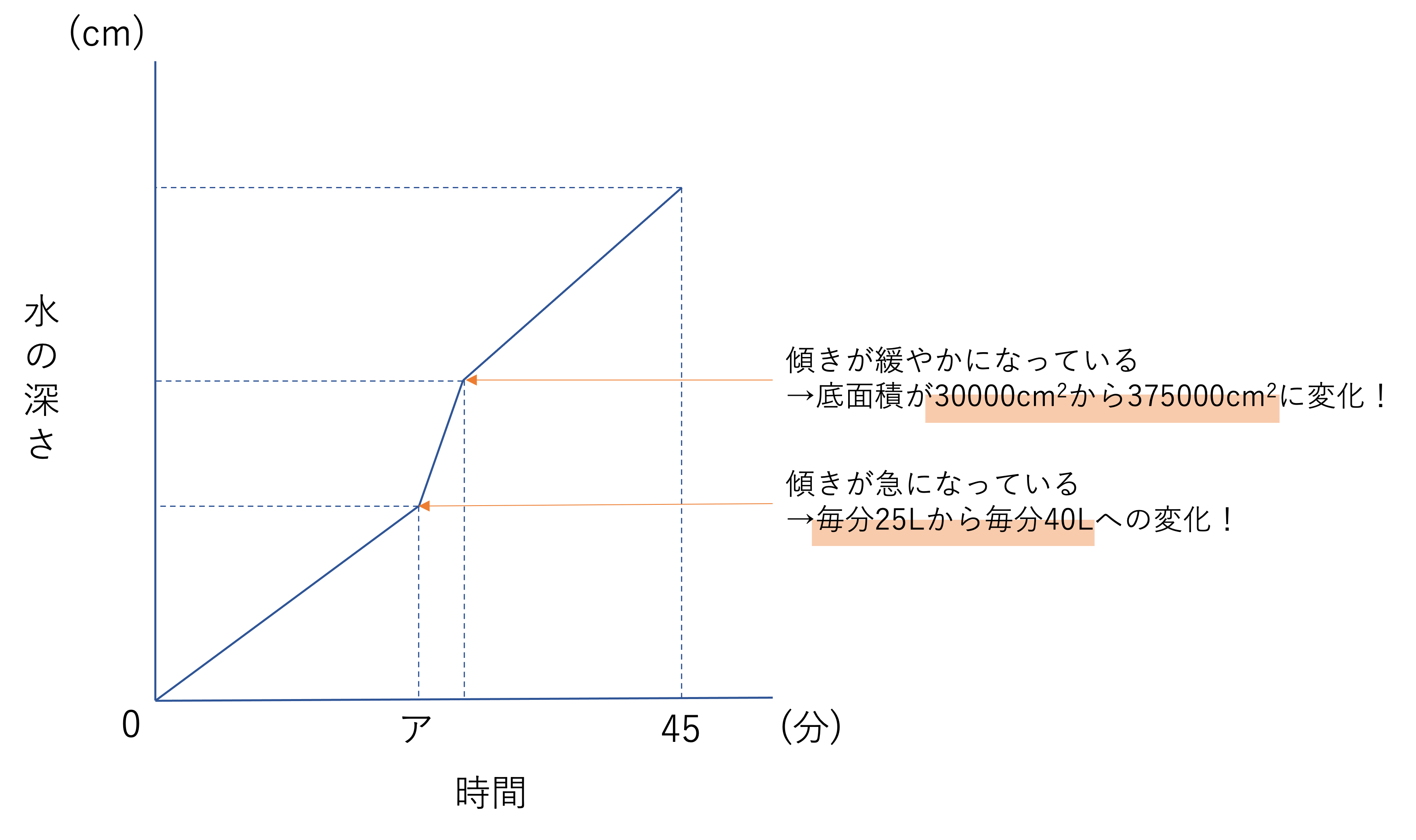
そして2つ目のステップとして大切なことは,グラフの転換点に注目するということです。今回の転換点とは,折れ線グラフの折れている部分を指します。今回の問題だと,時間がア(分)のところ・水の深さがイ(cm)であるところの2点で折れていますね。そして重要なのが,このグラフにおける折れているポイントとは水の溜まり具合の変化を表しているということです。この水の溜まり具合というのは水の注ぐ割合と容器の形の2点で変化するのですが,つまり今回の問題では2回溜まり具合が変化しているというわけです。そしてこのうち1回は前述した毎分25Lから毎分40Lへの割合の変化が挙げられるため,もう一つが容器の形の変化に基づいているというわけです。したがってグラフにおいて傾きが急になっている部分があれば,それは毎分25Lから毎分40Lに変化している瞬間を指していると判断できますね。この転換点への注目,ならびにその原因の特定が解答ステップの2つ目として重要なことです。頭に入れておきましょう。
ではこの複雑な形の変化による割合の転換は,一体どこで行われているのでしょうか。そこで注目するべき要素が図形の底面積の変化です。容積=底面積×高さの公式に基づくと,一定の量の水を水そうに入れていくとき,容器の底面積が小さければ水面はより高い位置になりますが,底面積が大きくなれば水面は低い位置になります。この関係をもとに今回の問題の容器を見ると,真ん中あたりでよこの長さが30cm伸びているので,途中で底面積が250×120=30000cm2から250×150=37500cm2になっていることがわかります。このことから,水を入れていく過程で高さが増えにくくなっている,つまりグラフの傾きが緩やかになっている瞬間があることが明らかになります。これらのことをまとめると,次のように情報を整理できますね。どういう要件で溜まり具合が変わるのか・急と緩やかのどちらに変わっていくのか,の2点を照合しながら情報をまとめていきましょう。
解説③計算に移ろう!
グラフと容器の形から水の溜まり方の大体の様子が判断できたところで,次は肝心の計算に移っていきましょう。このような問題があるとアの値を直接求めにいきたくなりますが,ここで重要なことが遠回りしてでも着実に計算できるところを順番に解いていくということです。今回の問題では,1回目の転換点である毎分25Lから毎分40Lへの変換のポイントに注目できそうなので,その部分から考えていきましょう。
この転換点ですが,問題文中で深さが20cmになったときに水を入れる割合を変えると言われていたことを思い出してみてください。このことからグラフに次のような情報を足していくことができます。このようなステップを一つずつ踏むことで,正しい答えを導いていきましょう。
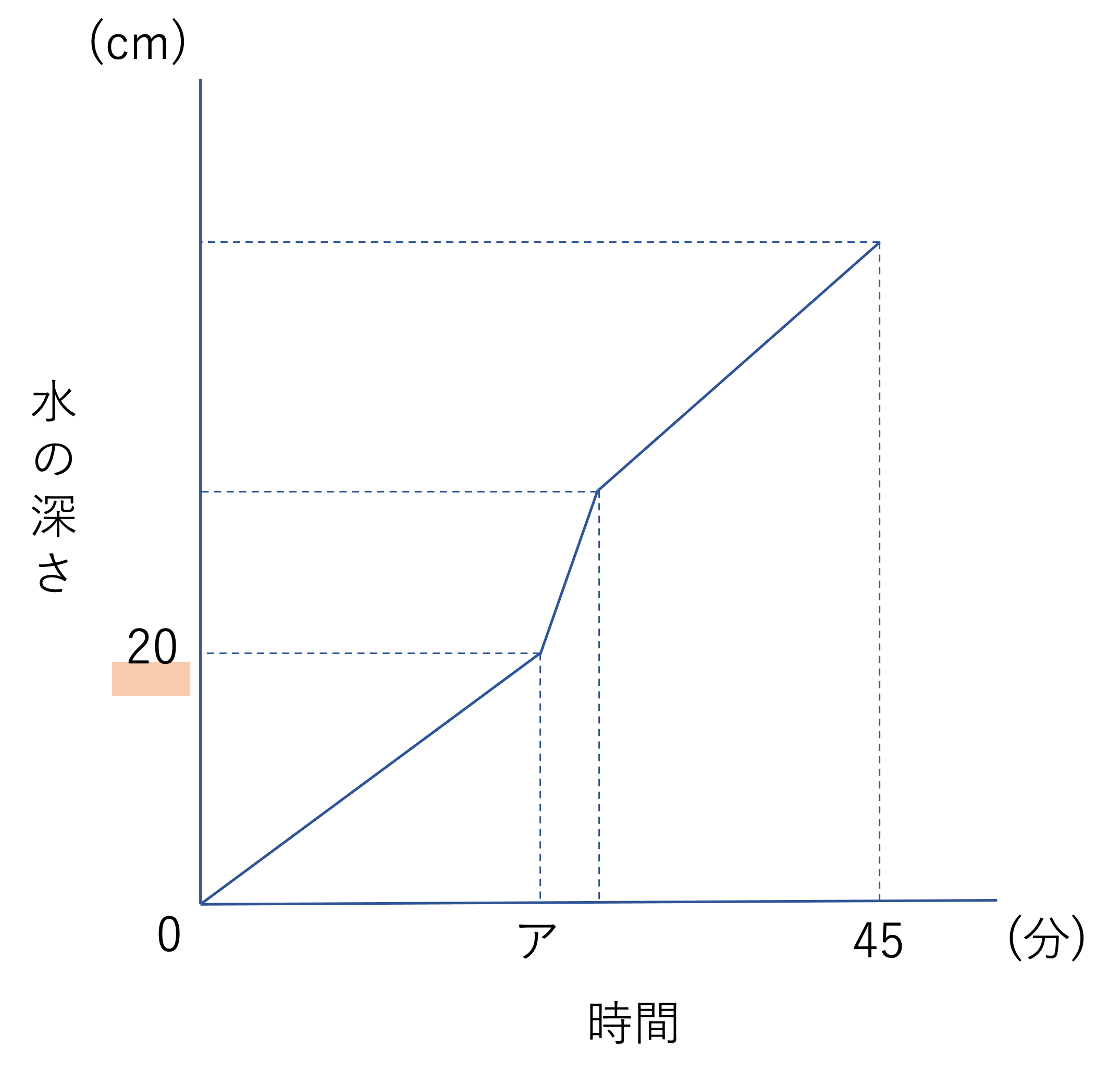
そしてこの情報があればアの値が計算できますね。底面積が30000cm2であり高さが20cmである容器の容積は30000×20=600000cm3ですね。他方水を入れる割合に注目すると,このとき1分あたりには25Lの水が入れられています。1cm3が1mLであることに注目し25Lの単位を25000mLに変換すると,600000cm3の容器に水を貯めるには600000÷25000=24分かかることが分かりますね。このように単位の変換などを行いながらかかる時間を計算していくと,アには24という数字が当てはまることが分かります。
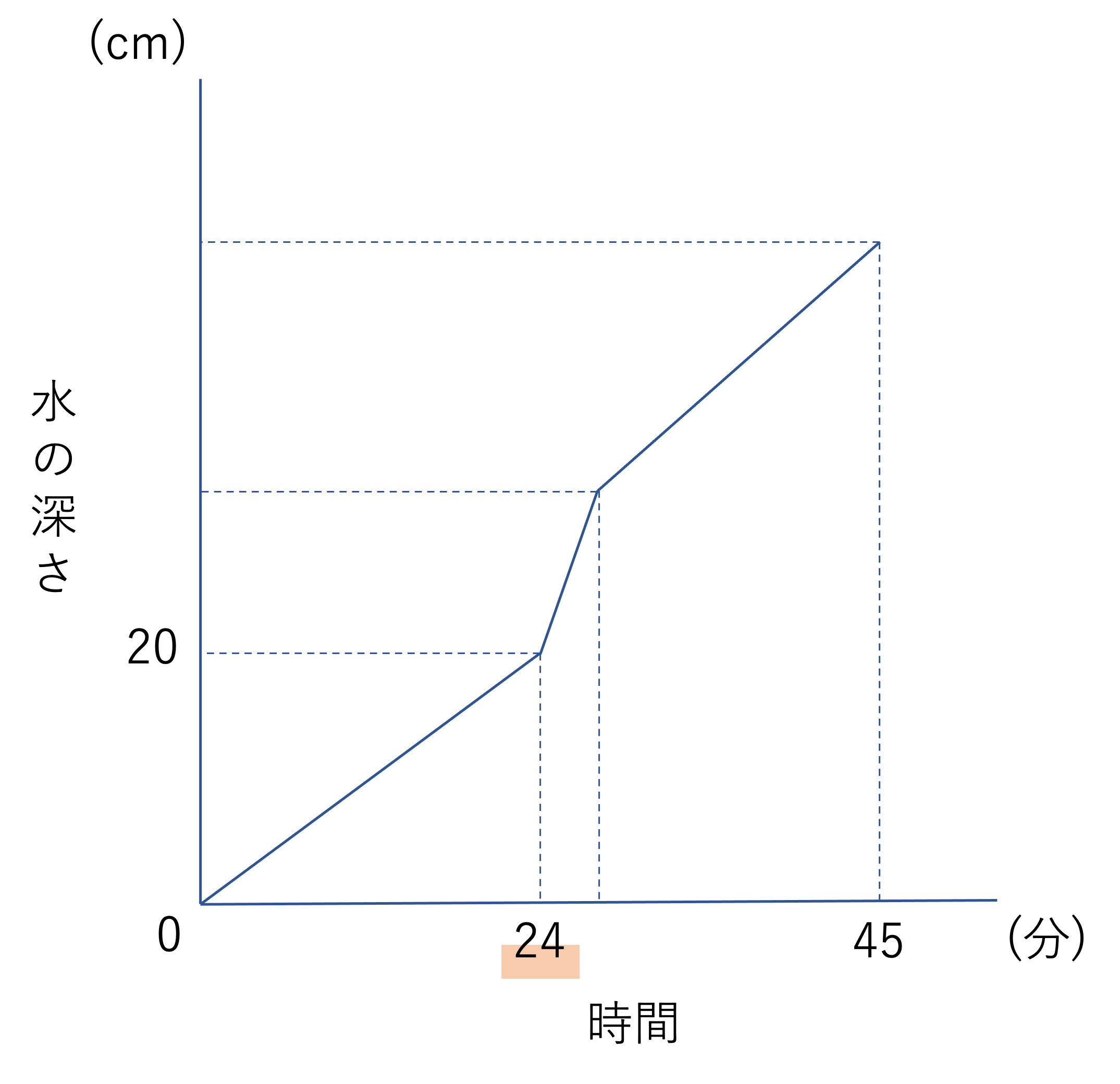
A.ア:24
まとめ
以上のような手順を踏むことで複雑な容器問題を解くことはできます。もちろん今回ご紹介したのは簡単な問題のほんの一部分でしかありませんが,グラフと図形の両方に対する視点が問題を解く上で重要であるということを理解していただけますと幸いです。改めて回答のポイントをまとめていきましょう。
- 問題文の中身をまずは整理しよう!
- 溜まり具合の転換点に注意しながら,グラフに情報を書き込もう!
- 着実にわかるところから計算を進めていこう!
終わりに
本記事ではこれまで,複雑な形をした容器の中に水を入れるというシチュエーションに即した問題の解説を行っていきました。この問題にはグラフと体積という2つの分野に対する理解が不可欠だという難しさがありますが,一方それはこの問題を解けるようになればグラフも体積も理解度を上げられることを指します。慌てずに落ち着いて演習を重ねていきましょう。本記事が今後の学習のお役に立てば幸いです。