密度の基本　～質量と重さの違い、密度とは何か、密度の大きさと浮き沈みの関係について知ろう～【練習問題付き】　

　物質の性質の1つとして 密度 があります。密度の求め方や周辺の測定実験なども含めて他の分野との複合問題として出題されることもあります。ここでは密度についての基本を学習しましょう。

密度

質量

　まず密度とは何かを確認する前に質量というものについて確認しておきましょう。

質量とは，物体そのものの分量を表す量のことです。単位は「g」や「kg」を用います。

皆さんにとって「g」や「kg」は「重さ」の単位というイメージが強いかもしれませんが，実はこれらは物体の「分量」を表す単位なのです。

しかしこれでは「質量」と「重さ」の違いがよく分からなくなってしまう方も多いと思います。

そこで次に改めて「重さ」とは何かということも確認していきましょう。

重さ

　質量と重さの違いをより明確にするために「重さ」というものの定義についても改めて確認しておきましょう。一部中学以降の内容を含むため，あまり深入りする必要はありません。

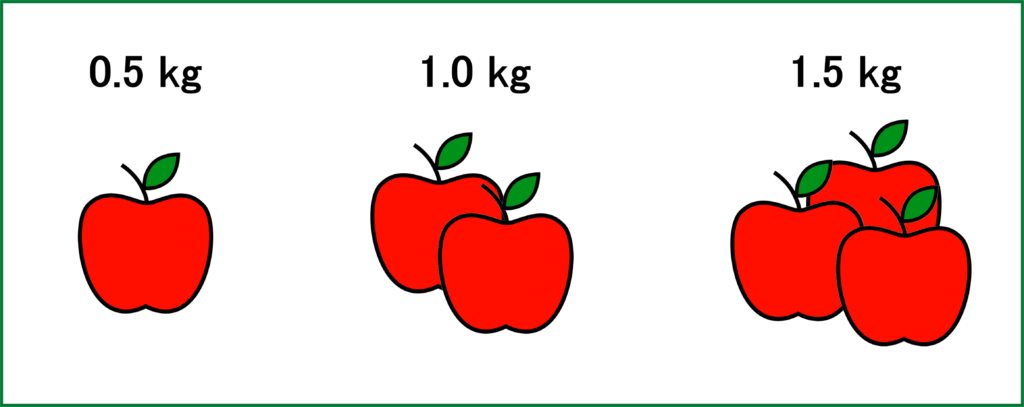
重さとは，物体が受ける重力の大きさのことです。単位は「N(ニュートン)」を用います。

つまり質量は物体の「分量」を表し，重さは物体が受ける「重力の大きさ」で，それぞれ定義が異なるのです。

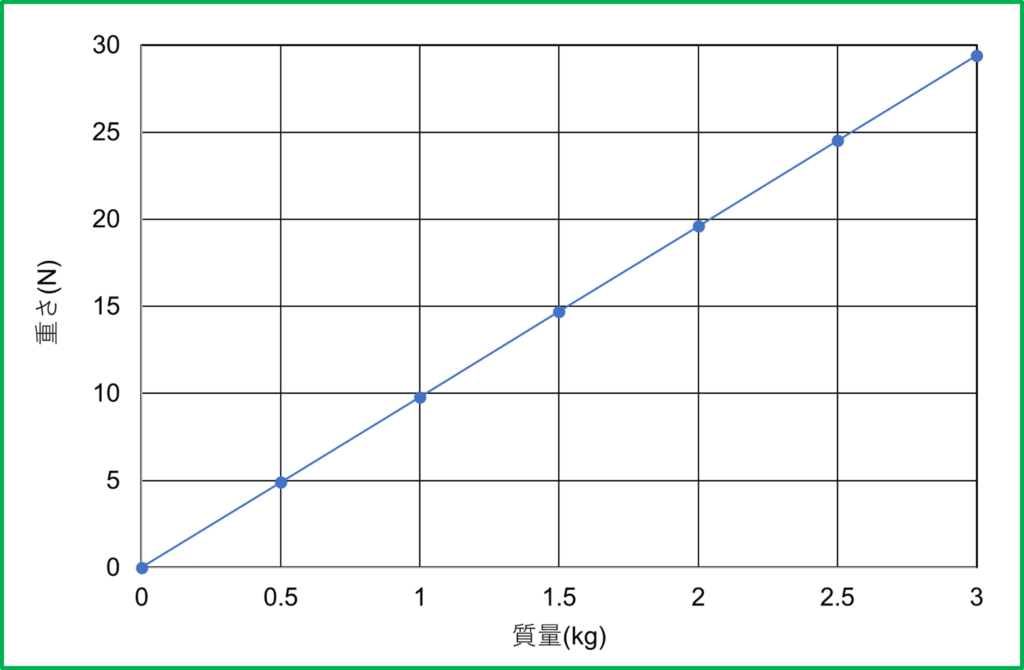
そして重さは質量に比例します。つまり物体の量である質量が2倍，3倍，…と増えれば物体の重さも2倍，3倍，…と増えるのです。だから質量を重さのように扱ってもその比は変わらないため都合よく使えるということになります。

(おまけ)質量と重さ

　ここで質量と重さの区別をより明確にするためにさらなる例について紹介します。理科を学習するうえでは非常に重要な内容ですが本題とはあまり関係がないので読み飛ばしてしまっても問題ありません。

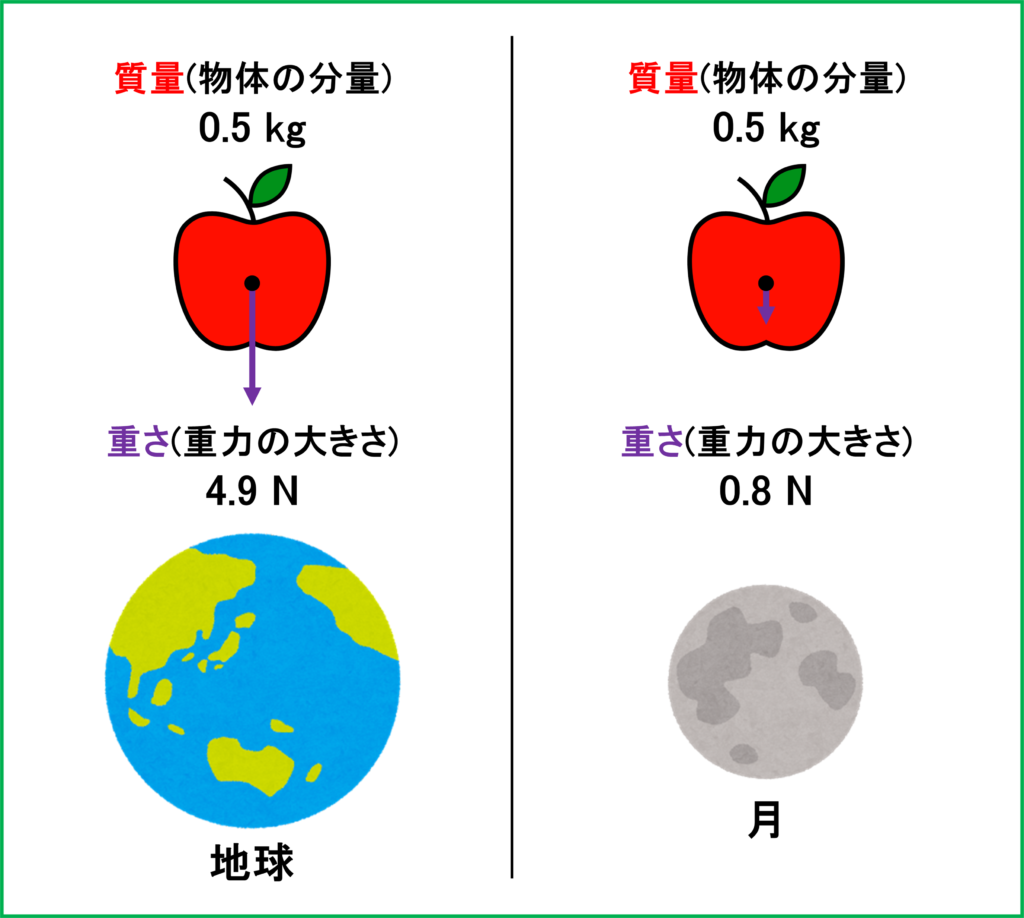
　皆さんはテレビや漫画などで「月に行くと重力が地球より軽い！」なんて話を聞いたことがあると思います。実際に物体が受ける「重力の大きさ」は月の方が小さいのです。

　ここで1つのりんごを想像してみましょう。地球から月に持って行ったとしても何もしなければりんごが突然半分になることはありません。

　つまり地球と月の間でりんごの分量，つまり質量は変化しません。しかし重さは違います。

　月では地球に比べて，物質が受ける重力の大きさが約6分の1になることが知られています。

　つまりりんごの「量」は変化しなくても，「重さ」に関していえばりんごは月にあるときより地球にあるときの方が6倍重いのです。

質量と重さの違いがなんとなく理解していただけたでしょうか。この質量というものを用いて次からは本題の密度について解説していきます。

密度 とは

　本題の密度とはどのようなものなのかを確認していきましょう。

密度とは，物体の質量を物体の体積で割ることで出る値のことで，単位体積あたりの質量のことを言います。

多くの場合は1cm³あたりの質量で表されます。基本的にはこちらで覚えていただいて問題ありません。

つまり1cm³という大きさの中にどれだけの分量の物体があるかということを示しています。

密度が大きければそれだけ物体がぎゅうぎゅうに詰まっているということですし，逆に密度が小さければ同じ大きさでも中身はスカスカということです。

密度は物質に特有の値を持っているため，「物体がどの物質からできているか」の1つの手掛かりにもなります。

密度 と浮き沈み

　皆さんは水に浮く物質と水に沈む物質の違いは何だと思いますか？

軽い物質が水に浮いて，重い物質は水に沈む。その考え方は半分くらいは正しいですが正確なものとは言えません。実は物質の浮き沈みには密度の大小が大きく関係しています。

正確には密度が小さい物質が浮き，密度の大きい物質が沈みます。

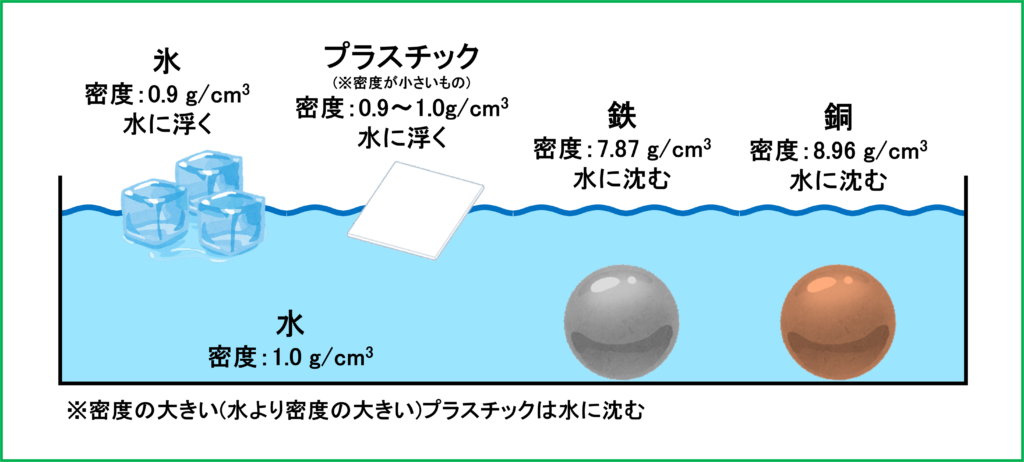
水の密度は1.0 g/cm³です。つまりこれよりも密度が小さい物質は浮き，密度が大きい物質は沈みます。

例えば「氷」は密度が約0.9 g/cm³なので水に浮き，「鉄」は密度が約7.9g/cm³なので水に沈みます。

水に入れる物質は固体である必要はありません。油など水と混ざらない液体であれば密度によって層に分かれます。一般的に油は水よりも密度が小さいため水に浮きます。

練習問題　密度

　上で学習したこと活かして練習問題を解いてみましょう。

問題

解答

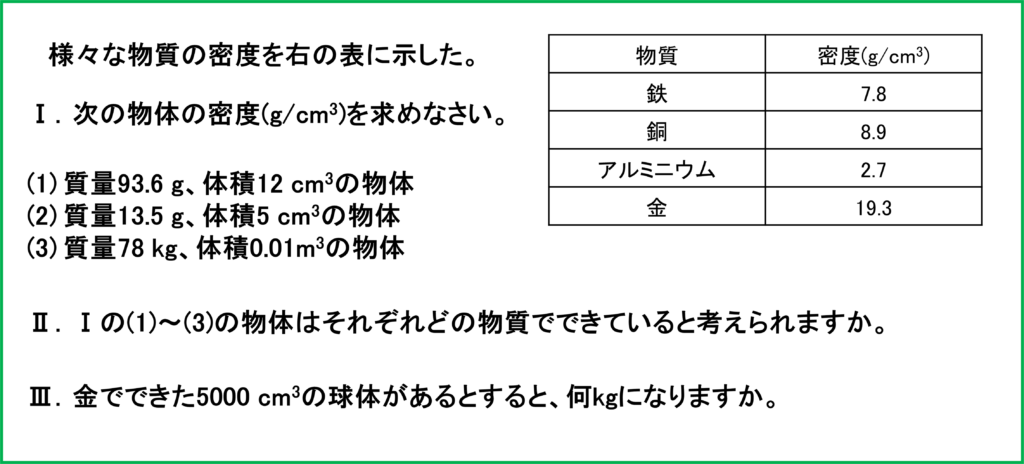
Ⅰ

• (1) 7.8 g/cm³　
• (2) 2.7 g/cm³　　　
• (3) 7.8 g/cm³

Ⅱ

• (1) 鉄　　　
• (2) アルミニウム　　　
• (3) 鉄

Ⅲ：9.65 kg

解説

Ⅰ

(1)
93.6÷12=7.8 よって7.8 g/cm³

(2)
13.5÷5=2.7 よって2.7 g/cm³

(3)
まずはそれぞれ単位の換算をする必要があります。

1 kg = 1000 gなので、78 kg = 78000 g

1 m³ = 1000000 cm³なので、0.01 m³ = 10000 cm³

この状態で計算すると78000÷10000 = 7.8 よって7.8 g/cm³

Ⅱ

表の値より(1)鉄、(2)アルミニウム、(3)鉄

Ⅲ

金の密度は19.3 g/cm³なので，1 cm³につき19.3 gの質量があるということです。

これが5000 cm³あるとなると，19.3×5000=9650 つまり9650 gあるということになります。

1 kg = 1000 gなので，9650 g = 9.65 kg となります。

入試問題演習　密度

　実際の入試問題を見てどのように密度の考え方を応用すればよいのかを見ていきましょう。

問題

解答

• 問1：D
• 問2：(1) ア　　(2) 密度：2.7 g/cm³　記号：C
• 問3：A
• 問4：(1) 89.5 g　　(2) 96.2 cm³
• 問5：カ

解説

問1
物体A～Dについて，それぞれ重さを体積で割って密度を計算すると次のようになります。

• 物質A：8.9 g/cm³
• 物質B：7.9 g/cm³
• 物質C：2.7 g/cm³
• 物質D：0.9 g/cm³

水に浮くためにはその密度が水よりも小さくなければならないので，物体A~Dのうち水に浮くのは物体Dのみとなります。

問2
(1)
まず水をメスシリンダーに入れた場合，液面の内側が少し下に沈むようなへこみ(メニスカス)ができます。

つまり選択肢のアやイのような液面が形成されます(物質によってはウやエのようになるときもあります)。

そしてメスシリンダーで物質の体積を測る場合，液面の内側の平らな部分の目盛りを読むことになっています。

今液面の内側の平らな部分が56の目盛りの部分にきてなければならないので問題の下線部を表す適切な図はアです。

(2)
メスシリンダーに水を張ったところに物質を入れると，入れた物質の体積分だけ全体の体積が増えるので，56 – 50 = 6 より，物体Eの体積は6cm³であることが分かります。

問題文から，物体Eの重さは16.2gなので，これを重さで割ると，16.2÷6=2.7となるため物体Eの密度は2.7g/cm³となります。

問1で計算した密度と比べると，物体Eは物体Cの密度と同じなので物体Eは物体Cと同じ材料でできていると分かります。

問3
密度が1cm³あたりの重さを表しているのならば，密度が大きい物質は小さな体積で大きな重さを稼げることになります。

つまり密度の異なる物質同士を同じ重さだけ用意しようとしたとき，密度の大きい物質が小さい堆積で済みます。つまり体積が最も小さくなるのは物体Aです。

問4
(1)
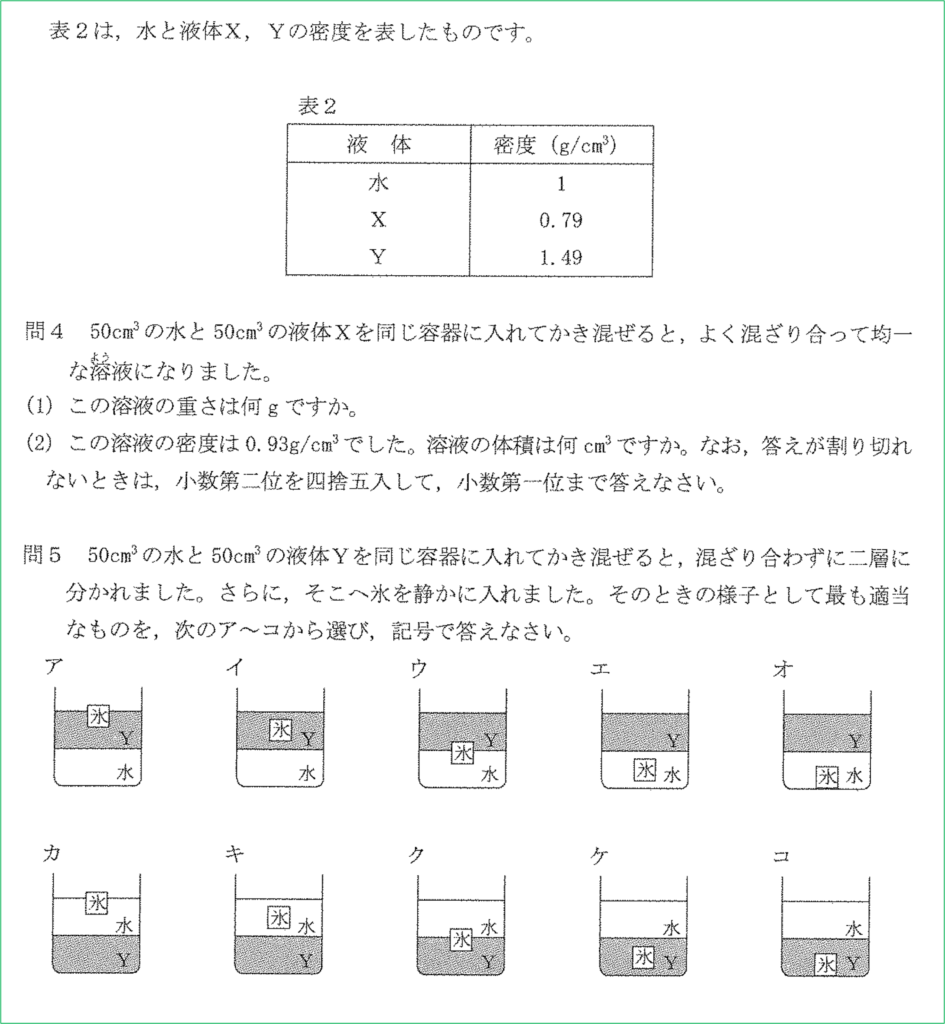
水50cm³の重さを計算すると，問題の表2から水の密度が1g/cm³だから，1×50=50より50gとなります。

次に液体X 50cm³の重さを計算すると，問題の表2から液体Xの密度が0.79g/cm³だから，0.79×50=39.5より39.5gとなります。

これらを足すと50+39.5=89.5となるため，求める液体の重さは89.5gとなります。

(2)
密度は重さを体積で割ると計算できるので，体積は重さを密度で割ることによって計算することができます。

(1)より溶液の重さは89.5gと計算しているので，これを溶液の密度0.93g/cm³で割ると，89.5÷0.93=96.23…≒96.2より溶液の体積は96.2cm³となります。

溶液が混ざるとき，重さは単純に加えればよいですが，体積は50cm³と50cm³を加えたからといって単純に足して100cm³になるわけではありません。溶液同士が相互作用して密度が変化します。

問5
表2より溶液Yは水よりも密度が大きいので水の下に沈むことになります。よってカ～コのいずれかになります。また氷は水よりも密度が小さいので水に浮きます。よってカが正しい図です。

関連サイト→https://chugaku-juken.com/math-ratio-basic/

おわりに

『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨

塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介！！

↓↓詳細は以下をタップ↓↓