この記事では力学の3 つの原理について述べる.教科書や参考書によってはニュートンの3 法則と書かれている場合もあるが,ここでは「原理」と書く.つまり何か別の法則から導かれることがなく,それらを前提するという意味を強調しておく.ただし,それぞれの原理の名前は慣習に従って,「法則」と表記する.
力学の第1原理:慣性の法則
慣性の法則とは,力を受けていない物体は慣性系において等速直線運動をするというものである.
まず慣性系の意味について述べる.慣性系の「系」の意味は「座標系」という意味である.座標系とは簡単に言うと,誰から見るかということである.慣性系とは,力を受けていない物体が等速直線運動する座標系のことである.
ここで注意してほしいのが,「等速直線運動」にはもともと静止していた(速さ0) 物体が静止し続けることも含まれているということである.
さて,この慣性の法則だが,初めて聞いた人からすると「そいうもんか」程度のものに思えるかもしれない.経験的に,水平な床でボールを転がすと同じ速度で運動し続けることを知っている人もいるだろう.(もちろん現実的には摩擦や空気抵抗があるので減速していずれ止まる.) だからなぜ「原理」にまでする必要があるのかと疑問に思うだろう.
そこで慣性の法則についてもう少し詳しく見ていこう.初めて力学を学ぶ場合は,立ち入るとかえって混乱するので) 次の第2 原理に移っても構わない.後に出て来る慣性力を学ぶときにでも見返してほしい.
今,等速直線運動をしていない物体を考えよう.例えば落下しているボールなどを思い浮かべればよい.もし物体と一緒に動く人(座標系) からそれを見ると,物体は静止(あるいは等速直線運動) しているように見えるはずだ.このように,見る人,すなわち座標系をうまく選んでやれば,力が働いていようがいまいが物体は等速直線運動と見なせる.するとこの座標系も慣性系であるように思える.
しかし,この座標系は慣性系でない.というのも,先ほどの物体とは別の等速直線運動している物体を考えたとき,最初の物体が等速直線運動しているように見える座標系から,他方の物体の運動を見ると,それは一般に等速直線運動をしていないからである.つまり,慣性系とは力が働いていない全ての物体が,等速直線運動をしている座標系のことであり,慣性の法則の主張(要請) は,そのような慣性系が存在することにある.
力学の第2原理:運動方程式
力学の第2 原理は,慣性系において,運動量の時間変化は力に等しいというものである.まず運動量\(\overrightarrow{p}\)は,質量\(m\),速度\(\overrightarrow{v}\)の物体に対して,
\(\overrightarrow{p} =m \overrightarrow{v}\) (1)と定義されるものである.速度がベクトルなので,運動量もベクトルである.
力学の第2 原理が言っていることは,この時間変化が力\(\overrightarrow{F}\)に等しいということだから,
\(\frac{d\overrightarrow{p}}{dt} = \overrightarrow{F}\) (2)となる.多くの場合は質量\(m\)は変化しないので1,以下のように書き直せる:
\(m \frac{d\overrightarrow{v}}{dt} = \overrightarrow{F}\) (3)この方程式を運動方程式という.速度や加速度の定義を思い出すと,運動方程式は,
\(m \overrightarrow{a} = \overrightarrow{F}\) (4)だとか,
\(m\frac{d^{2}\overrightarrow{x}}{dt^{2}} = \overrightarrow{F}\) (5)のように表せることも分かる.第2 原理が言っていることは,慣性系において運動方程式が成立することである.以下では説明を簡単にするため1 次元として考える.
まず運動方程式の意味を考えよう.運動方程式はイコールで結ばれているが,物理的な意味は両辺で等価ではない.右辺の力\(F\)が原因となって,左辺にあるような質量\(m\)の物体に加速度\(a\)という結果が生じるという因果関係を表している.だから,ある物体がある加速度で運動していたからといって,右辺の力が何かが分かるわけではない.
そして物体の運動は,この運動方程式によって決まる.だから,力学の問題では物体に働いている力を判断して運動方程式立て,それを解けば運動が予言できるのである2.具体的な運動方程式の解き方は後の記事で学ぶことにする.
とりあえず今は,物体の運動を知るには運動方程式を立てる必要があるということだけを認識しておこう.
さて,ここまで来て鋭い人は気付いたかもしれない.運動方程式において力が全く働いていない場合,加速度が0 になる.そして等速直線運動になる.これは力学の第1 原理と同じことではないかと.そうすると,力学の第1 原理は第2 原理の特別な場合のことを言っているだけになってしまう.わざわざ別の原理にする必要があるのか.
この問題の答えは第1 原理のところにも書いたように,慣性の法則はあくまで「慣性系の存在」を主張していることにある.第2 原理はそのような慣性系においては運動方程式が成立することを言っているのだ.だから第1 原理は第2 原理に含まれている訳ではないことに注意しよう.
力学の第3原理:作用・反作用の法則
作用・反作用の法則とは,2 つの物体が互い力を及ぼし合っている場合,それぞれに働く力は同じ大きさで逆向きであるというものである(以下の図).
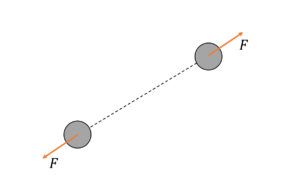
例えば,水面上で手漕ぎボートに乗っている人が,別の手漕ぎボートに乗っている人をある力で押すと,押した人も押された人も互いに反対方向に動き出す.これは押された人が受けた力と同じ大きさの力を,押した人が逆向きに受けるからである.他には銃を撃つと反動があるのは,作用・反作用の法則のためである.
1原子核反応では質量が増えたり減ったりする.
2正確には初期条件というものも必要.詳しくは後の記事を参照のこと.
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。