この記事では力学を学ぶ上で前提となる運動の記述の仕方について述べる．具体的には，そもそも力学における運動をどのように記述するか，そして位置や速度，加速度といったものがどのように定義されるかを見る．
物理を学ぶ意義
大層な見出しだが，そもそもなぜ物理を学ぶのかを疑問に思っている人向けの動機とな る(といいな) と思う内容を紹介する．もちろん，意義は人によって違うし，様々な意見 があって良いと思う．既に物理が大好きです，あるいは，物理を勉強するのに抵抗がない という人は，ここを呼び飛ばして先に進んでしまおう．
まず「物理」という漢字を見ると，物(もの) の理(ことわり) となっている．意味をく み取ると，この世界の現象の法則ということである．つまり物理を学ぶということは，こ の世界の物理法則=この世界の設計図を学ぶということである．物理の歴史をたどると， はじめは神が創造したこの世界がどのように創られたのかについて知りたいということ から始まっているようだ1．
さて，物理を学ぶということは，この世界の設計図を学ぶということだと述べたが，その設計図を学ぶことの何が嬉しいのか．多くの場合，設計図そのものに対する好奇心で 研究がなされているが，設計図を学ぶことの意義は他にもある．そのひとつが「予言」で ある．
予言なんて聞くと，怪しい占いか何かのように聞こえるかもしれないが，そうではな い．例えばボールを斜めに投げたとき，どのような軌道を描くかは実験してみれば分か る．しかし，物理法則を知っていれば投げる前からどのような軌道を描くか予言できるの だ．
これは簡単な例だが，もっと予言が役立つ例もある．例えば車を作る際に，試しに車 を作ってみて人を乗せて走らせたら事故になりました，では困る．車を作る前から，ある 程度どうなるかが分かるためには，物理法則を知っている必要がある．また，宇宙のこと だとか，実験が困難な場合も，物理法則にしたがって推測することができる2．
ところで現代社会では多くの情報が飛び回っている．その中にはそれらしい科学用語を 用いて，これは健康的に良いだとか，幸せになると宣伝してお金儲けをするような人もいる．たいていの場合，科学的に正しいなんて言われると信じてしまいそうだが，このようなものを自分で見極める能力が必要である．物理を通して，そのような情報に騙されない知識，思考力が多少は身につけられるはずである．
運動をどのように記述するか
力学と聞くと，何か物体が動いてその運動がどのようになっているかを学ぶのだろうという漠然としたイメージを持つだろう．教科書の最初の部分を見ると，「等速直線運動」だとか「等加速度運動」という言葉が登場する．ではその運動をどのように記述するのか．
あの有名なガリレイの言葉に，「この世界は数学という言語で書かれている」といった容のものがある．この言葉から分かるように，物理法則は全て数学を用いて記述される．数学があまり好きでない人はなんでわざわざ難しい数学を使うのかと思うかもしれない．むしろその逆なのである．人類は今のところこの世界の現象を記述できる道具として数学しか知らないのだ．そして今のところ数学でうまく説明ができているのだ．だからこれから登場する力学の運動も数学によって表現される必要がある．
さて，力学において「運動が分かった」とはどのようなことを意味するのだろうか．結論から言うと， 任意の時刻での位置と速度が求められれば，運動が分かったと言える．だから力学での最初の目的は，位置と速度を求めることにある．一連の力学を学べばどのようにしてそれらが求められるのかが分かるだろう．
そこでまずは，運動の記述に必要な位置，速度，加速度といったものの定義を確認しよう．「定義」はある現象を数式化するために覚えておかねばならないものである．だから自分で数式に落とし込めるように定義をしっかり定着させよう．
スカラーとベクトル
物理で登場する値を持つような対象(速度や密度，質量など)，すなわち物理量にはスカラーと呼ばれるものとベクトルと呼ばれるものがある．スカラーは大きさのみを持ち，ベクトルは大きさと向きを持つ物理量である3．高校物理の範囲では，ベクトルは成分に分けて考えるということだけ意識しておこう．
スカラーは例えば質量や密度，ベクトルは位置や速度などである．これらの分類には注意しておこう．というのも，物理の問題を解く際に大きさのみを答えるのか，向きまで答える必要があるのかを知っておくことはケアレスミスの防止にもつながるからである．
位置，速度，加速度の定義
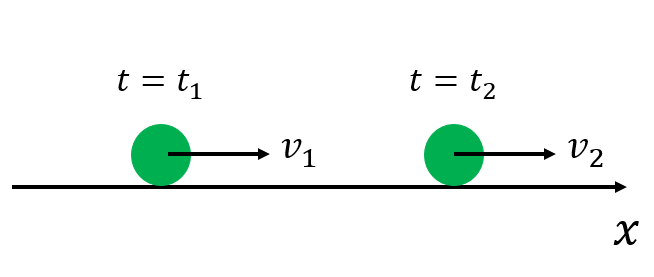
簡単のために1 次元で考えよう．まず以下の図のように右向きを正に\(x\)軸をとる．このように力学の問題では最初に座標の設定をしよう．座標を決めることで位置が決定される．位置はベクトルである．
今は1 次元で考えているので，成分を考える必要はない．(だからベクトルを表す矢印も省略してる．あるいはベクトル3 成分の内の\(x\) 成分のみに注目していると思ってもよい．)
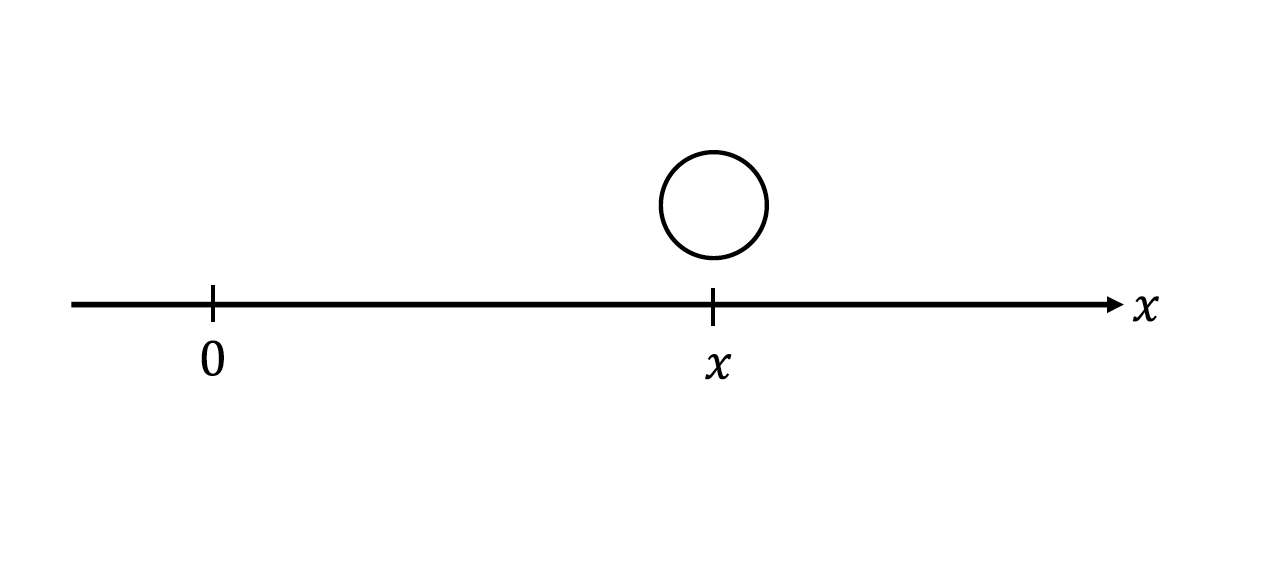
次に速度を定義しよう．小学生でも習うように，物体が動いた距離(位置の変化) を時間変化で割れば速さが求まる．しかし，100 mを10 s で4走ったからといって，ずっと10 m/sだったわけではない．より正確な速度を求めるには，速度を計測する時間間隔を短くする必要がある．これは後でも見るように，時間間隔を0 に近づける極限に相当する．
そこである時間間隔\(\Delta t\)の間に，位置\(x(t)\)が\(\Delta x\)変化したとすると，
と書ける．このように変化は「変化後」から「変化前」を差し引く．
これらを用いて速度\(v(t)\)を6以下のように定義する：
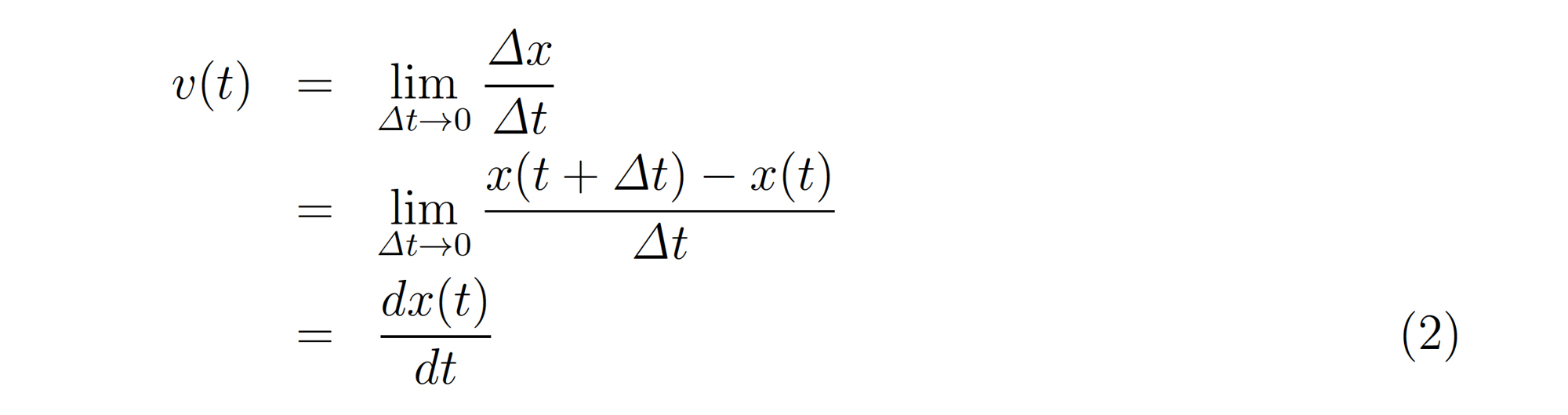
最後は数学で習う微分の定義そのものを用いた．このように，速度は位置の時間微分で定義される．微分を用いることに抵抗がある人がいるかもしれないが，そもそも微分は力学の基礎を築いたニュートンによって開発されたものである．しかも微分を用いることで「簡単に」速度が求められるのである．以下の例題を通して，計算に慣れよう．分からない計算は数学の教科書を参考にしてほしい．これ以降も数学を用いるが，高校数学の範囲を逸脱することはないので，数学の勉強も各自で行ってほしい．
ここで注意してほしいことがある．「速度」と言った場合はベクトルだが，「速さ」と言った場合は速度の大きさのことを意味し，スカラーである．問題で問われているものが速度なのか速さなのかに注意しよう．
例題
以下のように表される位置\(x(t)\)に対して，速度\(v(t)\)を求めよ．なお，\(C\)，\(D\)，\(\omega\)，\(\lambda\)は定数を，\(e\)は自然対数の底を表すものとする．
(1) \(x(t)\) = \(C t\) + \(D\)
(2) \(x(t)\) = \(C t\)2 + \(D t\)
(3) \(x(t)\) = \(C sin(\omega t)\)
(4) \(x(t)\) = \(C cos(\omega t)\)
(5) \(x(t)\) = \(C e\) \(\lambda t\)
解答
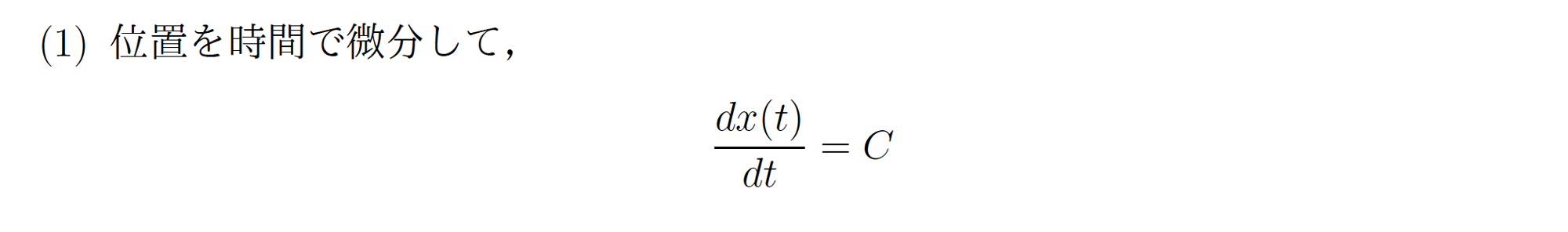
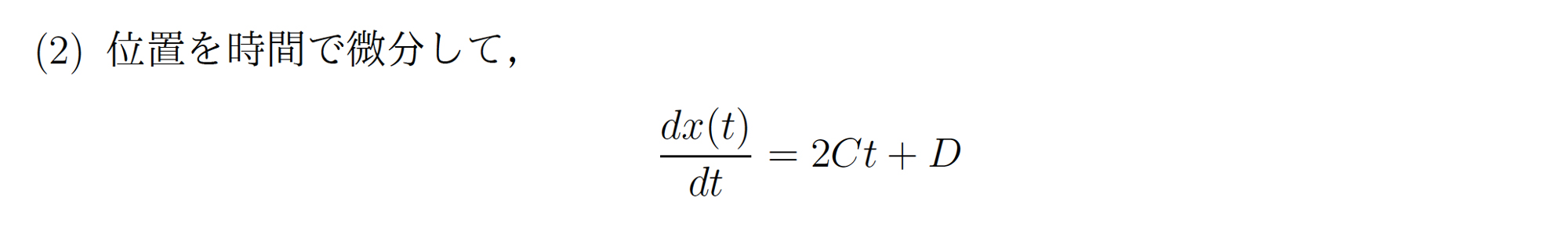
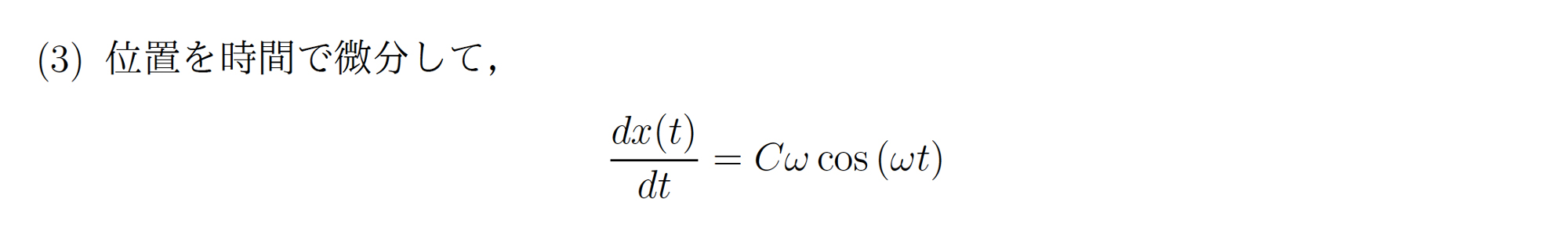
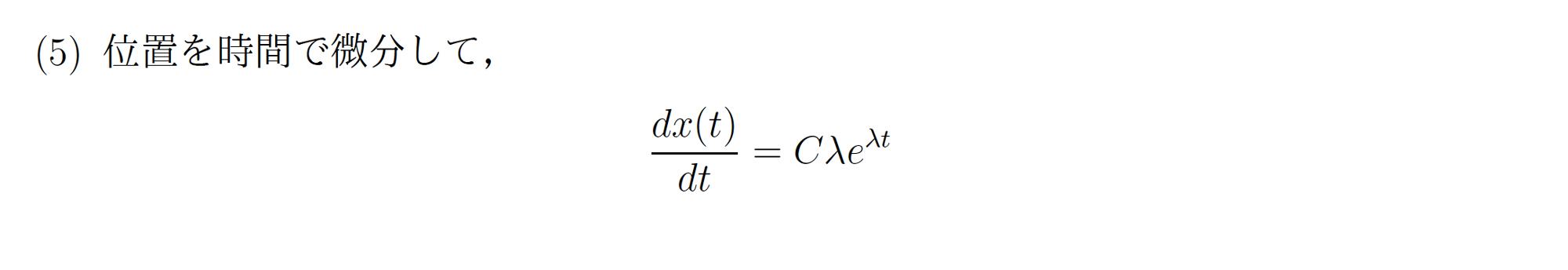
次に加速度を定義しよう．速度は，ある微小時間変化に対する位置の変化であった．加速度\(a(t)\)は7それを繰り返し，ある微小時間変化に対する速度の変化で定義される：
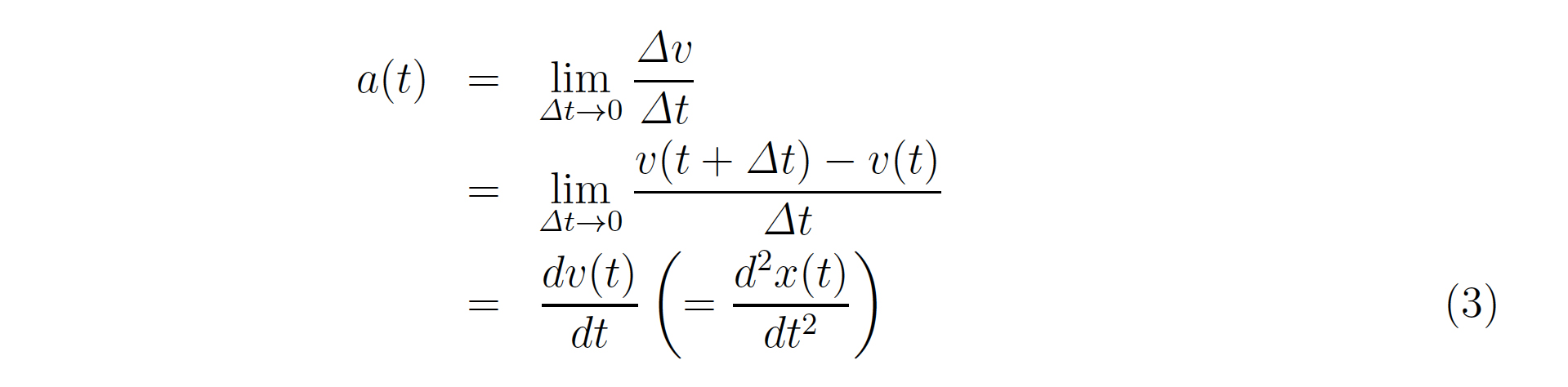
最後の表式は，速度を使う場合と位置を使う場合があるので注意してほしい．だから加速度も速度を時間で1 度微分するか，位置を時間で2 度微分するかで求めることができる．また，今まで1 次元として考えてきたが3 次元の場合も，それぞれの成分に対して同様に計算すればよい．
変位，速度，加速度の関係
以上より位置を時間で微分すると速度，速度を時間で微分すると加速度が得られることが分かった．そこで今度はその逆を考えてみよう．つまり「微分の逆の操作」である積分を計算する．
まず加速度\(a(t)\)を時間で積分する．ここで積分は定積分を考える．だから積分範囲を決めてあげる必要がある．
はじめの時刻を\(t\)0，最後の時刻を任意の時刻\(t\)とすると，
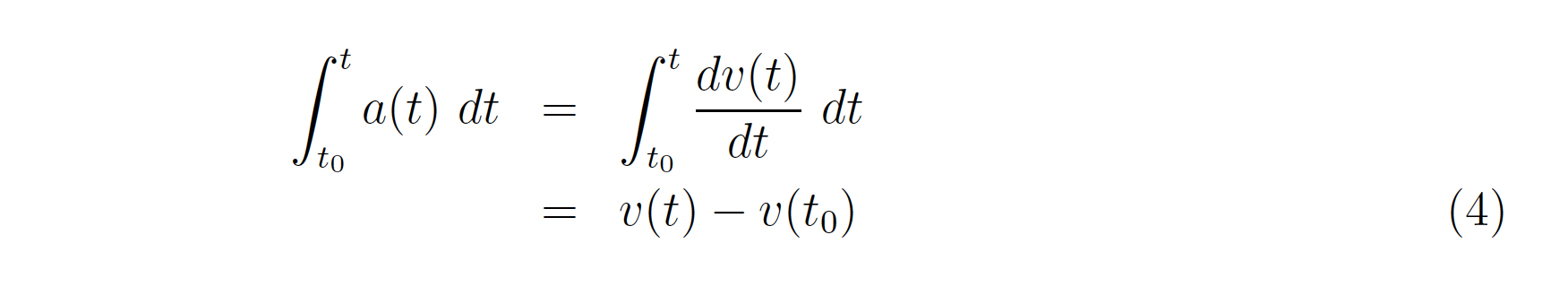
となる8．最後の変形は置換積分の形(正しくはないが\(dt\)を「約分できる」形) に注目して積分を実行した．つまり，加速度を時間で定積分すると速度の変化が得られる．このように積分を考えると，求めたい速度\(v(t)\)に加えて初速度\(v(t\)0)も出て来る．
同様に速度を時間で積分すると，
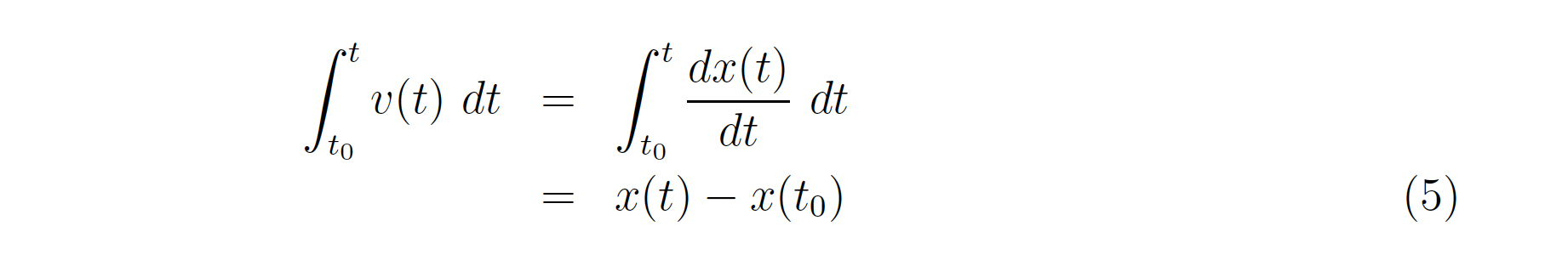
となり，速度を時間で定積分すると位置の変化(変位) が得られる．
以上から分かることは，加速度，速度，位置のどれか1 つが分かってしまえば，微分や積分を用いることで他の2 つも求まってしまうということである．
例題
以下のように表される加速度\(a(t)\)に対して，速度\(v(t)\)と位置\(x(t)\)を求めよ．ただし\(C\)，\(g\)，\(\omega\)，\(\lambda\)は定数であり，時刻\(t\) = 0 に速度\(v(0)\) = \(v\)0，位置\(x(0)\) = \(x\)0であったとする．
(1) \(a(t) = -g\)
(2) \(a(t) = Ct\)2
解答
1科学史の本などを読むと，必ずしも科学と宗教が対立の構造にあったわけではないということが分かる．
2物理法則から理論的に予測したことが必ずしも正しいとは限らない．推測が正しいかは実験や観測で検証する必要がある．ある時代では正しいと思われていた物理法則が，後の時代に修正されることは多い．しかし適用範囲を限定すれば十分に正しい．
3(発展) 実はこれらの他にも分類が存在する．その際の分類は，座標に対して「変換」を行ったときの変換の仕方に応じて定義される．例えば，スカラーは座標回転をしても値が変わらないもの，ベクトルは座標回転で大きさは変わらないが，向きは変わるものとして定義する．
4s は秒を表す．second の頭文字．
5このように微小な変化を表すのに\(\delta\) (デルタ) を頭につける．
6velocity の頭文字．
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。
