Contents
イオン結合の紹介
イオン結合の結晶とは
+の陽イオンと-の陰イオンがクーロン力によって引きつけ合っているイオン結合の結晶。
+と-が規則正しく配列し、そのくり返し単位を単位格子という。
配列のしかたは多種に及ぶが、ここではNaCl型とCsCl型のみを紹介する。
NaCl型の単位格子
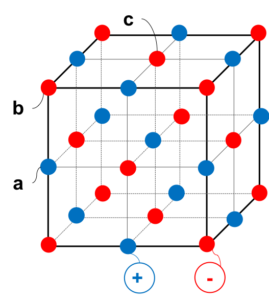
図1
図1のように立方体の各頂点および各面の中心に-イオン、各辺の中心に+イオンが配置され、+と-が交互に並んでいるのがNaCl型である。

図2
まずは、この1コの単位格子中に+イオン、-イオンがそれぞれ何コずつあるかを考えたい。これは単純に左の図の●の数を数えれば良いのではない。
なぜならば、左の構造が延々と繰り返されており、他の単位格子と共有している球もあるからである。
たとえばaの位置の球は4つの単位格子と共有され図2のようになっているので、1つの単位格子あたりは1/4コと数えるべきである。
同様に考え、bの球は1/8コと数え、cの球は1/2コと数える。
すると、単位格子あたり
+イオン → 1/4 × 12 + 1 × 1 = 4コ
-イオン → 1/8 × 8 + 1/2 × 6 = 4コ
入っているとカウントできる。
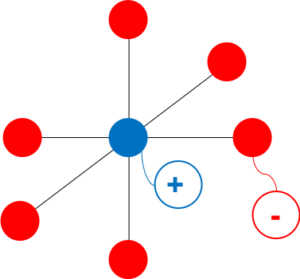
図3
次に、1コの+イオンがいくつの-イオンに囲まれているかを考える。
これは配位数と呼ばれており、単位格子の中心を拡大した図3より6コと分かる。
そして繰り返される単位格子の対称性から明らかに-イオンの配位数も6コである。
CsCl型の単位格子
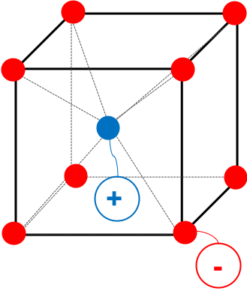
図4
図4のように立方体の各頂点に、-イオン、立方体の中心に+イオンが配置された、くり返し構造がCsCl型である。
単位格子1つあたりに
+イオン → 1コ
-イオン → 1/8 × 8 = 1コ
入っているとカウントできる。
また、CsCl型も8コ並べてみると分かるが、+イオンと-イオンの間に対称性があり、配位数は+イオンも-イオンもともに8である。
- Ex) NaCl結晶の密度は何g/cm3か?(Na=23、Cl=35.5、単位格子の1辺は56nm)
単位格子1つあたりにNaCl分子は4分子=\(\frac{4}{6.0\times10^{23}}\)mol含まれているので
\(\frac{4}{6.0\times10^{23}}\times58.5\)gの重さである。ところで単位格子1つの体積は(0.56nm)3=(5.6×10-8)3cm3
なので\(\frac{\frac{4}{6.0\times10^{23}}}{(5.6\times10^{-8})^{3}}\) ≒2.2g/cm3 と求まる。
※1nm = 1.0×10-9mである。よく出てくるので覚えておこう。
イオン結晶の限界半径比
イオン結晶の限界半径比とは
イオン結晶が安定な配列をするためには、+イオンと-イオンが接しなければならない。
いま、1章で見たようにイオンの大きさとしては+イオン<-イオン(∵ 中心の陽子の+が大きいほどクーロン力が大きくて半径が小さい)であるから、
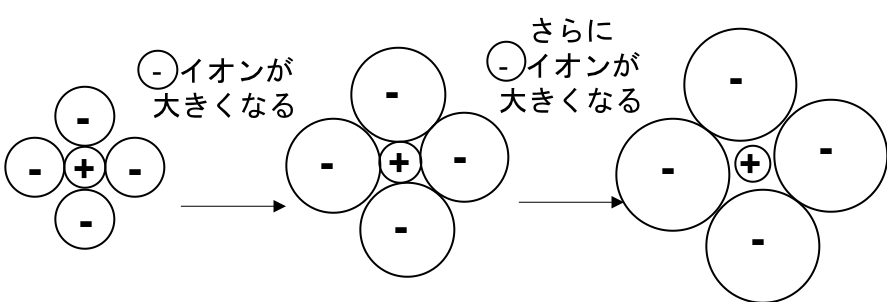
図5
安定 ギリギリ安定 不安定
(-と+のみ接している) (-と-、-と+が接する) (-と-のみ接している)
のように、-イオンと+イオンの半径比r+/r-がある程度以上でないと安定にならないことがわかる。(-イオンが+イオンに対して大きすぎるとNG)ということなので、NaCl型、CsCl型それぞれにつきギリギリどの半径比まで許されるのか(=限界半径比という)を考えてみる。
NaCl型の限界半径比
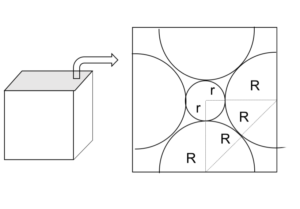
図6
限界になるように、+と-、-と-が接しているような図で考える。
NaCl型の立方体の任意の一面を取り出して、+の半径をr、-の半径をRとおく。
あとは図形的にrとRの関係式を導いていく。
1:1:√2の直角二等辺三角形に注目し、
(R+R) = √2(r+R)
↔︎ r/R = √2-1
≒0.41
つまりr/R ≧ 0.41の範囲でないとNaCl型は安定にならない。
CsCl型の限界半径比

図7
図7のグレーの面を取り出して、+と-、-と-が接している図を考える。
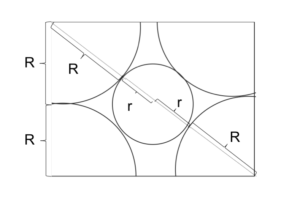
図8
1:√2:√3の直角三角形に注目し、
(R+r+r+R) = √3(R+R)
↔︎ r/R = √3-1
≒0.73
つまり、r/R ≧ 0.73の範囲でないとCsCl型は安定にならない。
この2つの結果から、陽イオンの半径と陰イオンの半径比r/Rが0.41≦r/R≦0.73ならNaCl型になりやすいと考えられる。
このようにイオン結晶は構成する陽イオンと陰イオンの半径比で、どのような単位格子型を取るのかが決まっている。(他にもCuCl型、CaF2型、Cu2O型など様々あり)
イオン結晶の特徴(復習)
- 融点が高い → イオン結合はクーロン力によって強く結びついており、バラバラにしてとかすのに大きな熱エネルギーを必要とする。
- 電気を通さない → +や-はかたい結合で結びついており、動けないから。しかし水に溶かしたり融解させると、動けるようになって電気が流れるようになる。
- へき開性がある → 何らかの力が加わって一層ずれると、+と+、-と-が隣同士になって、大きな反発により壊れてしまう。そのため、層状に結合が切れやすいもろさがある。
共有結合性結晶の特徴(復習)
共有結合の結晶には、共有結合性結晶と分子結晶の2種類があった。
共有結合性結晶は、主にCやSiのように4本の腕があるものが、四重結合が取れないため無限に全て共有結合でつながって、結晶となっているものである。
代表的なものにダイヤモンドと黒鉛がある。
- ダイヤモンド→すべてのCが4コの価電子をすべて結合に使い、正四面体の立方的な構造になったもの。とてもかたく、融点はきわめて高い。
価電子がすべて結合に使われてしまっておち、電気を通さない。
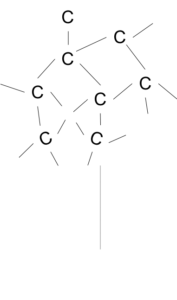
図9
- 黒鉛→Cのもつ4つの価電子のうち、3つのみを結合に使い、正六角形の連なった平面構造をとる。1コ価電子が余っているため、電気を流すことができる。また、平面と平面の間は、共有結合に比べてとても弱い分子間力がはたらいており、そのため平面に沿ってはがれやすい。
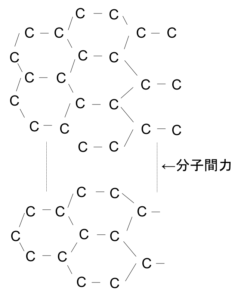
図10
分子結晶の特徴(復習)
ほとんどの共有結合化合物は分子という1グループを作って安定化し、その分子同士が弱い分子間力によって結びついて結晶となっている。
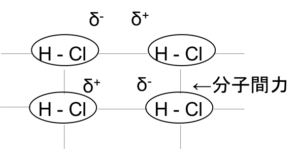
図11
分子間力とは極性分子のδ+とδ–の間ではたらく弱いクーロン力であるファンデルワールス力、無極性分子の一瞬の電荷のかたよりではたらくロンドン力、HとF、HとN、HとOという電気陰性度の大きく異なる原子間にはたらくやや強い水素結合の3つからなる。
分子間力は弱いため、分子結晶はどれも融点・沸点は低いが、その中でもやや強い水素結合を含むものは融点・沸点が高い。δ+、δ–なので電気は通さない。
金属結晶の紹介
金属はいらない価電子を押し付け合って結晶化する際、できるだけ金属が密に規則正しく詰まって配列する。
その単位格子の配列のしかたは複数あるが、ここでは代表的な体心立方格子、面心立方格子、六方最密構造の3つを紹介する。
- 体心立方格子

図12
図12のようにイオン結晶のCsCl型のような金属の配列のしかたを体心立方格子という。
単位格子1コに含まれる金属は 1/8 × 8 + 1 = 2コで配位数は8である。 - 面心立方格子

図13
図13のようにイオン結晶のNaCl型の片方のイオンのように、立方体の各頂点と各面の中心に金属が配列したものを面心立方格子という。
単位格子1コに含まれる金属は1/8 × 8 + 1/2 × 6 = 4コで
配位数は12 である。
配位数は図14の●で考えるとその上、その面、その下に4つずつで計12コと数えられる。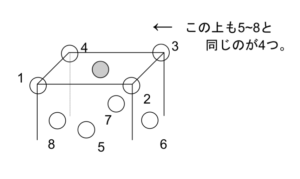
図14
- 六方最密構造

図15
図15のような金属配列のしかたを六方最密構造という。点線で図のように区切ると体心立方格子のような形のものが3つ合わさったものということが分かり、その1つ分を単位格子とみなす。
単位格子1コに含まれる金属は1/12 × 4 + 1/6 × 4 + 1 = 2コで
配位数は12である。
配位数は図16の●で考えると、その上、その面、その下に4つずつで計12コと数えられる。
図16
金属結晶の充填率
単位格子1コの体積のうち、金属の体積が何%を占めているのかで、どれくらい金属が密に詰まっているのかを表したものを充填率という。
※密度 → g/cm3 、 充填率 → cm3/cm3より%計算なので注意!
- 体心立方格子
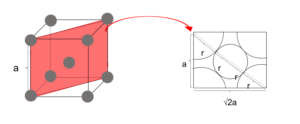
図17
単位格子の1辺をaとする。金属球の半径をrとする。
図より 4r = √3a
∴ r =\(\frac{\sqrt{3}}{4}a\)
(密に詰まっているので球と球が接する図を書く。)
いま、単位格子の体積はa3、金属球の体積の合計は、
\(\frac{4}{3}πr^{3}\)×2コ =\(\frac{8}{3}πr^{3}\)
=\(\frac{8}{3}π\times(\frac{\sqrt{3}a}{4})^{3}\)
これより、充填率は \(\frac{\frac{8}{3}π\times(\frac{\sqrt{3}a}{4})^{3}}{a^{3}}\)×100 ≒ 68% と求まる。 - 面心立方格子
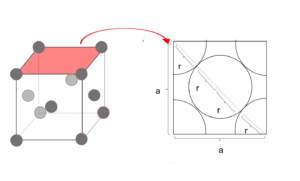
図18
図より 4r = √2a
∴ r =\(\frac{\sqrt{2}}{4}a\)
いま、単位格子の体積はa3
金属球の体積の合計は、
\(\frac{4}{3}πr^{3}\)×4コ = \(\frac{16}{3}πr^{3}\)
=\(\frac{16}{3}πr^{3}\times(\frac{\sqrt{2}}{4}a)^{3}\)
これより、充填率は\(\frac{\frac{16}{3}πr^{3}\times(\frac{\sqrt{2}}{4}a)^{3}}{a^{3}}\)×100 ≒ 74% と求まる。
※六方最密は難しいので、省略するが、これも充填率は74%である。
金属結晶の特徴(復習)
- 金属光沢がある → 表面を流れる自由電子の光の反射により、表面がキラキラしている。
- 熱や電気をよく通す → 自由電子が動けるため。
- 展性・延性に富む → 結合のもとが自由電子なので、割と自由に伸ばせる。
規則性の無い結晶
いままで見てきた結晶とは異なり、原子・分子の配列に規則性が無いものをアモルファスという。アモルファスの代表としてはガラスが有名である。
ガラスはもともと共有結合性結晶であるSiO2(石英)を約2000℃に加熱してそれを凝固することで得られる。