Contents
反応速度の定義
化学反応には中和反応のように一瞬で起こるものもあれば、鉄が空気中でさびる酸化反応のようにゆっくりと起こるものもある。
この、「一瞬」や「ゆっくり」のような、反応の速さは以下のように、
「反応物または生成物の単位時間あたりの濃度の変化量」
で定義させている。
A → 2B
反応前 [A0]mol/L [B0]mol/L
t秒後 [At]mol/L [Bt]mol/L
上図のような化学反応の反応速度vは
Aの減少速度に注目すると、
\(v_{A} = \frac{[A_{0}]-[A_{t}]}{t} = \frac{-Δ[A]}{Δt}\)
と表される。
Bの減少速度に注目すると、
\(v_{B} = \frac{[B_{0}]-[B_{t}]}{t} = \frac{-Δ[B]}{Δt}\)
と表される。
※いま、Aが1mol減少するとBが2mol生成するので、2Δ[A]=Δ[B]であるため、2VA=VBとなっている。
なお、反応速度は一定ではなく、時間経過具合によって変化する。たとえば、2H2O2→2H2O + O2と過酸化水素が分解する反応において、各時間のH2O2の濃度が以下の表にように変化したとする。
|
時間(min) |
濃度(mol/L) |
|
0 |
0.675 |
|
2 |
0.556 |
|
4 |
0.458 |
|
6 |
0.372 |
0分から2分までの平均の反応速度は、
\(-\frac{0.556-0.675}{2-0} = 0.060 mol/L・min\)
また、4分から6分までの平均の反応速度は、
\(-\frac{0.372-0.458}{6-4} = 0.043 mol/L・min\)
となり、反応が進むにつれて平均の反応速度が小さくなっていっている。
反応速度式
“⑴反応速度の定義”では、ある時間t0秒後と、ある時間t1秒後を比べ、その濃度変化の割合から平均の反応速度というのを考えたが、今度はある時間t2を指定した時にその瞬間の反応速度をどう考えたらいいかという一般式を見ていく。
たとえばA+B→Cという化学反応があった時、その反応の反応速度はその時点の残りのAの濃度とBの濃度に比例することが分かっており、
\(v=k[A]^{a}[B]^{b}\)
の形になる。(直感的にも反応物の濃度を大きくしたら、反応速度も大きくなるのは納得しやすい。)これを反応速度式といい、\(k\)はその実験条件に固有の比例定数であり、反応速度定数とよばれている。
また、指数のa、bがいくつになるかは実験によって求めるしかない。
※指数a、bは反応式A、Bの係数に等しいと書いてある参考書を見かけるが、全くの間違いであるので気を付けること。(反応が一段階反応の時のみ一致する。)
- Ex) 2H2O2 → 2H2O + O2 の反応速度式を求めよ。ただし、この実験は3回行い、それぞれの濃度と速度は以下のようになった。
[H2O2] v
1回目
0.1mol/L
0.03mol/L・s
2回目
0.2mol/L
0.06mol/L・s
3回目
0.3mol/L
0.09mol/L・s
これより、H2O2の濃度はvと一次比例しているので、
\(v=k[H_{2}O_{2}]\)
→H2O2の係数は2だが2乗ではない!
★発展
H2O2の係数が2なので一見すると、H2O2の濃度を2倍にすると22=4倍の速度になりそうだが、ならないのは、この反応が二段階反応だからである。
触媒としてMnO2を入れることで、この反応は進行するが、まずH2O2がMnO2とくっついてから、分解反応が進行する。
この際、分解反応の段階では、\(v=k[H_{2}O_{2}]^{2}\)であるが、MnO2とくっつくはじめの段階では\(v=k[H_{2}O_{2}]\)である。
しかも、MnO2とくっつくことがこの反応において最も時間のかかる、律速段階であることから、2乗ではなく、1乗で比例している。
- Ex2) 2NO + Br2 → 2NOBrの反応速度式を求めよ。ただし、4回実験を行った時のデータを以下に示す。
[NO] [Br2] V
1回目
0.1
0.1
0.006
2回目
0.2
0.1
0.024
3回目
0.1
0.2
0.012
4回目
0.2
0.2
0.048
[NO]を2倍にすると、vが4倍になり、[Br2]を2倍にするとvが2倍になっていることから、反応式は、
\(v=k[NO]^{2}[Br]\) - Ex3) 2N2O5 → 4NO2 + O2の反応の反応速度式はで表せる。反応開始時のN2O5の濃度は5.02mol/Lであったとすると、反応速度定数[/min]はいくらか?
0分後から4分後までの平均の反応速度vは、定義より
\(v=-\frac{4.20-5.02}{4-0}=0.205 mol/L・min\)
である。
また、0分後から4分後までの平均のN2O5の濃度[N2O5]は、
\(v=-\frac{(5.02+4.20)}{2}=4.61 mol/L\)
である。よって
\(v=k[N_{2}O_{5}]\)
に代入して、
\(0.205=k[/min]\times4.61\)
より、
\(k=4.45\times10^{-2}/min\)
おまけとして…
H2 + Br2 → 2HBrという反応の反応速度式について考えてみる。
ここまで見てきた通り、1段階反応かどうかは分からないことから
などと指数を係数から判断してはいけない。
実際、この反応の反応速度式は
\(v=\frac{k[H_{2}][Br_{2}]^{\frac{1}{2}}}{1+m\frac{[HBr]}{Br_{2}}}\)
(m,kは定数)
の形で表される。
というのもこの反応は3stepからなるとても複雑な反応だからである。
触媒をMとすると、
- 開始反応 Br2 + M → 2Br + M (Br2の解離)
- 伝播反応 Br + H2 → HBr + H
- 伝播反応Ⅱ H + Br2 → HBr + Br
なお、①、②の逆反応である抑制反応と停止反応についても合わせて考え、
\(\frac{d[HBr]}{dt}\)、\(\frac{d[H]}{dt}\)、\(\frac{d[Br]}{dt}\)の三式を立てることで上に書いたvは求めるが、ここでは詳細は割愛する。
詳しくは大学2~3年生で。
反応のメカニズム
たとえば、H2 + I2 → 2HIという反応について、反応のメカニズムを考えてみる。
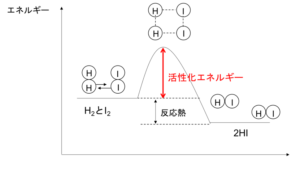
図1
この反応は、H2分子とI2分子がうまく衝突し、H-H結合およびI-I結合が切れるという不安定な状態を一回経由した後に、H-I結合が形成され安定な状態へ移行する。図1のようなエネルギー図で見ると分かりやすい。
この図にあるように、H-H結合、I-I結合が切れながら、H-I結合を形成しようとする、一瞬の不安定な状態をとる。これを活性化状態という。また、この活性化状態をとるために超えなければならない壁となるエネルギーを活性化エネルギーという。
そのため、この反応がどのくらい進行するかは、どのくらい多くの分子が衝突によって活性化エネルギーの壁を超えられるかにかかっている。
反応速度を大きくする条件
化学反応の反応速度を大きくするには3つの方法がある。
- 反応物の濃度を大きくする
反応物の濃度を大きくすると、活性化エネルギーを超えようと挑戦する分子の母数が多くなるので、必然的に成功して超えられる分子数も多くなる。
実際、\(v=k[A]^{a}[B]^{b}\)より、[A]や[B]を大きくするとも大きくなる。なお、同じ理由から固体の反応なら粉末状にして表面積を大きくしてあげることで反応速度は大きくなる。 - 温度を上げる
温度を上げると、分子の熱運動が激しくなるため、より多くの運動エネルギーを分子が持つため、活性化エネルギーを超えやすくなる。
反応速度式でいうとにあたる部分が温度に依存している。
※分子はすべて同じエネルギーを持っているわけではなく、高いエネルギーを持っている分子もいれば低いエネルギーを持っている分子もいる。
これらは統計的にボルツマン分布という確率のようなものに従って数が分布している。高温にすると、全体的に高エネルギーを持つ分子数が多くなる。
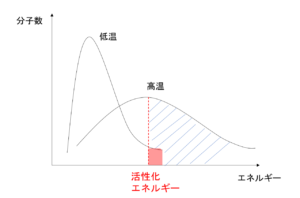
図2
図2の赤と青を比較しても、活性化エネルギーを超える分子の数は高温の方が多い。 - 触媒を加える
触媒というのは反応前後で形や量に変化はないものの、反応経路を変えて反応の手助けをしてくれる物質のことである。
これにより、活性化エネルギーが小さくなり、活性化状態の山を超えやすくなるので、反応速度が大きくなる。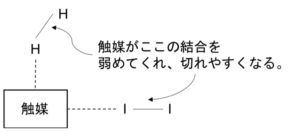
図3
反応速度式でいうと\(k\)が活性化エネルギーに依存している。
なお、触媒は反応経路を変えるだけで、反応物と生成物のエネルギーは変わらないため、反応熱はそのままである。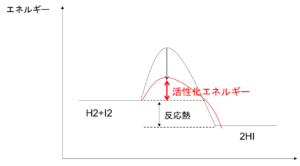
図4
★発展 ※〈アレニウスの式〉
“⑷反応速度を大きくする条件”で見たように、速度定数は活性化エネルギーが小さいほど大きくなり、温度が高くなるほど大きくなる。
これをより具体的に研究し、アレニウスは
\(k=Ae^-{\frac{E_{a}}{RT}}↔︎\log k = -\frac{E_{a}}{RT} + \log A \)
(Aは頻度因子とよばれる定数。Eaは活性化エネルギー、Rは気体定数、Tは絶対温度)
と、kが表されることを発見した。これをアレニウスの式という。
この式を利用すると、異なる温度T1とT2で反応速度定数k1、k2を求めることで、(これは⑵のEx3で計算した)以下のようなグラフを書くことができる。
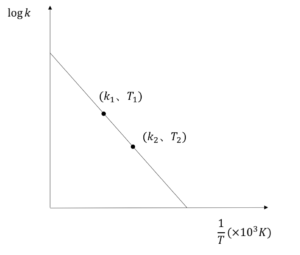
図5
\(\log k = -\frac{E_{a}}{R} ・ \frac{1}{T} + \log A \)
を、
\(y=-\frac{E_{a}}{R}・x + \log A\)
のように読みかえる。
すると、縦軸を\(\log k\)、横軸を\(\frac{1}{T}\)として複数のT、kを代入すると直線がひける。これをアレニウスプロットをいう。
この直線のy切片からAが、傾きからEaを求めることができる。
可逆反応と化学平衡
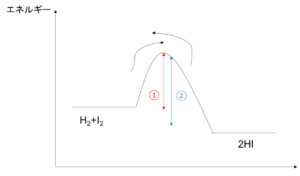
図6
再びH2 + I2 → 2HIの反応を考えてみる。
この反応は、H2分子とI2分子が衝突することによって、結合の組み換えが起こってHI分子が生成するのだった。
この反応の活性化エネルギーは左図の①である。
その一方で、生成したHI分子同士が衝突してH2分子とI2分子に戻ることも考えられる。
2HI → H2 + I2
この反応の活性化エネルギーは図6の②である。
つまり、H2分子とI2分子を混ぜて高温で放置しておくと、どちら向きの反応も起こる。
このような反応を可逆反応といい、H2 + I2 ⇄ 2HI のように表記する。
なお、→向きの反応を正反応、←向きの反応を逆反応という。
一方、→向きの正反応しか起こらない反応を不可逆反応という。
おもに開放状態で気体が発生する反応は逆向きはムリな不可逆反応である。
- Ex) C + O2 → CO2 は不可逆反応
ここで、気液平衡や溶解平衡の時と同じように、H2 + I2 ⇄ 2HIの反応を長時間放置しておいた時のことを考えてみる。
はじめは、H2とI2しかないので正反応の速度v正が大きいが、だんだんとHIが生成するにつれて逆反応の速度v逆が大きくなっていく一方で、正反応の速度は小さくなっていく。
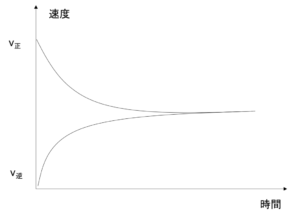
図7
そうすると、図7のようにv正= v逆となった時に見かけ上反応が止まったようにみえる。
このように、正反応でも逆反応も起きているにも関わらず共に反応速度が等しいために変化が無いようにみえる状態を平衡状態という。
これが可逆反応を最終状態である。
平衡定数
平衡定数とは
H2 + I2 ⇄ 2HIの反応が平衡状態にある時、温度が一定なら初期状態がどうであれ、
\(\frac{[HI]^{2}}{[H_{2}][I_{2}]} = (一定) = K\)
という関係が成り立つ。この定数を平衡定数とよぶ。
一般化すると、
\(aA+bB+…⇄mM+nN+…\)
という平衡において、
\(\frac{[M]^{m}[N]^{n}}{[A]^{a}[B]^{b}}=(一定)=K’\)
が成立する。左辺のモル濃度の積が分母で右辺のモル濃度の積が分子になる。反応速度式との大きな違いは、各物質の係数が指数と一致する点である。
直感的に分かりやすい導入を紹介しておく。
H2 + I2 ⇄ 2HI の
正反応の反応速度式は\(v_{正}=k_{正}[H_{2}][I_{2}]\)である。
逆反応の反応速度式は\(v_{逆}=k_{逆}[HI]^{2}\)である。
平衡状態では\(v_{正}=v_{逆}\)なので、
\(v_{正}[H_{2}][I_{2}]=k_{逆}[HI]^{2}\)→\(\frac{k_{正}}{k_{逆}} = \frac{[HI]^{2}}{[H_{2}][I_{2}]}\)
\(\frac{k_{正}}{k_{逆}}\)は、定数なので一定K
★超発展
なぜ\(v=k[A]^{a}[B]^{b}\)のa、bは係数とせず、実験から求めなければいけないのに平衡定数における指数は係数と一致するのか?
そもそも、反応速度定数を考える時に係数としていけないのは、その反応が実は多段階反応の可能性があるからであった。前と同じ例で
2H2O2 → 2H2O + O2 の反応を触媒MnO2下で行いことで考える。
この反応は、
①H2O2がMnO2とくっつく。
②①でくっついたものが分解する。
の2段階から起こる。
ここで、①は触媒の反応なので、触媒は量が関係ないため、\(v_{①}=k_{①}[H_{2}O_{2}]\)である。
②は分解なので、係数の2が直接関係し、
である。
いま、②よりはるかに①は時間がかかることから、実質反応の速さは①によって決まる(これを律速段階という)ので、
としていた。(①+②≒①)
しかし平衡においては、①の平衡定数と②の平衡定数の積が全体の平衡定数となるため、和が全体の速さになるのとは状況が違う。
今回、①はH2O2が触媒MnO2とくっついてH2O2’になるとすると、
より
\(平衡定数K_{①}=\frac{k_{①}}{k_{①}’}=\frac{[H_{2}O_{2}’]}{[H_{2}O_{2}]}\)であり、②は
\(k_{②}'[H_{2}O_{2}’]=k_{②}[H_{2}O]^{2}[O_{2}]\)より
\(平衡定数K_{②}=\frac{k_{②}’}{k_{②}}=\frac{[H_{2}O]^{2}[O_{2}]}{[H_{2}O_{2}]}\)である。
したがって中間体\(H_{2}O_{2}’\)を消去するために、
\(K_{①}^{2} \times K_{②} より K = \frac{[H_{2}O]^{2}[O_{2}]}{[H_{2}O_{2}]^{2}}\)よりとなる。
このように中間体を経ても、中間体を消去するように平衡定数の積を取ってあげることで、もとの反応式の係数と指数が一致する。
→すなわち、多段階反応において反応速度は各段階の和を取るが、平衡定数は各段階の積を取るという違いがある!
練習問題
高温の密閉容器にH2とI2を2mol入れて放置したところ、HIが1mol生成したところで平衡になった。
- この温度での平衡定数は?
- 同温の別の容器にHIのみを5mol入れて放置すると、H2が何mol生成して平衡状態になるか?
【解答】

式1
より、容器の体積をとすると平衡定数Kは、\(K = \frac{[HI]^{2} }{[H_{2} ][O_{2} ]} = \frac{(\frac{1}{V} )^{2} }{ \frac{1.5}{V} ・\frac{1.5}{V} } = \frac{4}{9} ≒ 0.44\)

式2
いま、⑴と同温なので平衡定数は一定の\(\frac{4}{9}\)であり、
\(\frac{4}{9} = \frac{(5- \frac{2x}{V} )^{2} }{\frac{x}{V} ・\frac{x}{V} } \)
∴ \(4x^{2} = 9(5- 2x^{2} )^{2}\)、
\(x> 0、5- 2x> 0\)
より
\(2x= 3(5-2x)\)
∴\(x ≒1.87mol\)
※C(固体) + H2O ⇄ CO + H2 のように固体がからむ平衡においては、固体の濃度は変わらないため、定数であり、平衡定数に組み込んで
\(K’=\frac{[CO][H_{2}]}{H_{2}O}\)
と表すことになっている。
圧平衡定数
気体に関する平衡反応を考える。
たとえば、N2 + 3H2 ⇄ 2NH3 という反応を考えてみる。いま、この反応の平衡定数は(気体:\(PV=nRT⇔\frac{P}{RT}=\frac{n}{V}\)←モル濃度[mol/L]を用いて)
\(=\frac{(\frac{P_{NH_{3}}}{RT})^{2}}{\frac{P_{N_{2}}}{RT}・(\frac{P_{H_{2}}}{RT})^{3}}\)
\(=\frac{P_{NH_{3}}^{2}}{P_{N_{2}}・P_{H_{2}}^{3}}・(RT)^{2}\)
\(K_{p}\) 定数
と変形できる。
この時、各物質の部夏に関して、平衡定数に対応する\(K_{p}\)も一定となる。
この\(あ\)を圧平衡定数といい、気体の平衡を考える際に用いることがある。
- Ex) N2O4(g)はN2O4(g) ⇄ 2NO2(g) の平衡が成立する。ある温度で容器に2molのN2O4を入れたところ、NO2が1mol発生したところで平衡状態になった。この時、容器内の圧力が1.0×104Paであったとすると、圧平衡定数はいくらか。
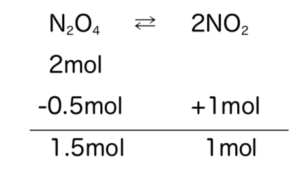
式3
いま、は一定なのでドルトンの分圧則より、(モル比)=(分圧比)となる。
よって、
\(P_{N_{2}O_{4}}=1.0\times10^{4}\times \frac{3}{5} =6.0\times10^{3}Pa \)
\(P_{NO_{2}}=1.0\times10^{4}\times\frac{2}{5}=4.0\times10^{3}Pa\)
である。
∴\(K_{p}=\frac{(P_{NO_{2}})^2}{P_{N_{2}O_{4}}}=\frac{(6.0\times10^{3})^{2}}{4.0\times10^{3}}=9.0\times10^{3}Pa\)
ルシャトリエの原理
ルシャトリエの原理とは
〈ルシャトリエの原理〉
化学反応が平衡状態にある時、濃度・圧力・温度などの反応条件を変化させると、その変化をやわらげる方向に反応がすすみ、新しい平衡状態になる。
たとえば、N2 + 3H2 ⇄ 2NH3 という平衡反応を例として考えてみる。
- 物質の濃度を増やす⇨その物質を減らす方向に平衡が移動
物質の濃度を減らす⇨その物質が増える方向に平衡が移動
・N2を加える
→N2を減らす方向に反応がすすみ、平衡は右へ移動する
・NH3を取り除く
→NH3を生成する方向に反応がすすみ、平衡は右へ移動する
実際平衡定数は一定なので
\(\frac{[NH_{3}]^{2}}{[N_{2}][H_{2}]^{3}}=(一定)\)
より\([N_{2}]\)を大きくしても値を同じにするには、\([NH_{3}]\)も大きくしていくしかない。 - 温度を上げる⇨温度が下がる吸熱方向に平衡が移動
温度を下げる⇨温度が上がる発熱方向に平衡が移動
・温度を上げる
→N2(g) + 3H2(g) = 2NH3(g) + 92kJという発熱反応なので、吸熱方向である左に平衡が移動する。
・温度を下げる
→発熱方向である右に平衡が移動する。 - 圧力を加える⇨分子数が少ない方向へ平衡が移動
圧力を減らす⇨分子数が多くなる方向へ平衡が移動
・圧力を加える
→圧力を減らす方向に反応がすすむ。いま、が一定でを減らすにはを小さくするしかないので、分子数を減らせば良い。
ここで、この反応は右方向にすすむと4分子→2分子と分子数が減るので分圧が減る。よって平衡が右に移動する。
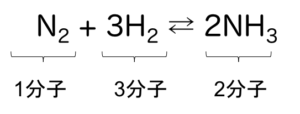
図8
・圧力を減らす
→分子数が2→4分子へと増える左に平衡が移動する。
※触媒を加えると平衡に達するまでの時間は短くなるが、反応結果自体に影響を及ぼさないので、平衡は移動しない。
また、固体がからむ平衡(C+H2O⇄CO+H2など)に関しては、固体の量を増減させても平衡は移動しない。
これは、固体は結晶の配列が決まっているため濃度が一定だからである。
練習問題
平衡はどう移動するか?
- N2 + O2 ⇄ 2NO [加圧する]
- C + H2O ⇄ CO + H2 [減圧する]
- N2O4 ⇄ 2NO2 -57kJ [温度を下げる]
- NH3 + H2O ⇄ NH4+ + OH– [NH4Clを加える]
- 2NH3 ⇄ N2 + 3H2 [触媒を加える]
- 2O3 ⇄ 2O2 [加圧する]
- NH3 + H2O ⇄ NH4+ + OH– [H2Oを加える]
- N2 + 3H2 ⇄ 2NH3 [体積一定でHeを加える]
- N2 + 3H2 ⇄ 2NH3 [圧力一定でHeを加える]
【解答】
- 2分子⇄2分子より平衡は移動しない。
- 固体は濃度一定なのでCは含めず1分子⇄2分子より、右に移動する。
- 発熱方向である左に移動。
- NH4ClはNH4+とCl–から出来ているので、NH4+を減らす左に移動。
- 平衡は移動しない。
- 2分子⇄3分子より左に移動。
- 右に移動する。
- Heの分圧は増えるが(は比例) N2・H2・NH3の分圧は変わらないので平衡は移動しない。
- 全圧は一定で、Heの分圧が生じることから、N2・H2・NH3の分圧はそれぞれ減る。よって減圧なので4分子⇄2分子から加圧方向の左へ移動する。
おすすめ記事
参考