6.気体の状態方程式〜理想気体の状態方程式を利用できるようになろう〜[大学受験化学-理論化学]| 中学受験ナビ

物質の三態(発展)

物質には主に気体、液体、固体の3つの状態にある。
この状態の違いは分子の熱運動の激しさの差によるものである。
分子の熱運動とは
…分子1つ1つがあちこち動き回ること。

この運動の激しさが実は温度の定義であるが、直感的には熱エネルギーを加えれば加えるほど運動エネルギーが大きくなり、激しく熱運動する、と考えてよい

図1

粒子が規則正しく配列　　　　　　粒子が一部動き回る　　　　　　粒子自由にあちこち動く

　粒子間の引力>熱運動　　　　　　粒子間の引力≒熱運動　　　　　粒子間の引力<熱運動

エントロピー小　　　　　　　　　　　　　　　　　　　　　　　　　　　エントロピー大

一般に熱を加えていくと気体になりやすいのは熱運動が激しくなることで粒子間の引力を振り切って粒子が運動をはじめるからである。
また、物質の乱雑さをエントロピーという。密に集合している状態ではエントロピーが小さく、あちこちに動き回っている状態は乱雑とみなし、エントロピーは大きい。
我々が放っておくと部屋が散らかるように、エントロピーも増大する方向が安定である。液体を放置すると蒸発するのはこのためである。(新しい学習指導要領ではエントロピーも高校範囲になるためこの説明を付しておいた。)

★★超発展
エントロピーは大きい方が安定なのにすべての固体が気体にならないのは、物質の安定さを考えるためにはエンタルピーという熱に関する概念も同時に考えなければならないからである。
エントロピーが増大することで安定になるエネルギー量と、そのために熱が必要であるというマイナスをてんびんにかけて考えなければならない。熱に関しては9章で詳しく扱う！

このように固体・液体・気体のそれぞれを6章~8章で1つずつ詳しく見ていく。

Contents

1 蒸気圧とは…?
2 ボイル・シャルルの法則
3 理想気体の状態方程式
4 ドルトンの分圧の法則
5 実在気体と圧縮因子
6 おすすめ記事
7 参考

蒸気圧とは…?

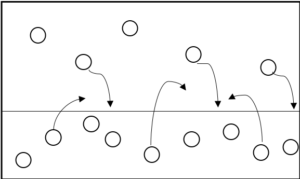
図2

密閉容器に液体を入れておくと、液体になっていた分子が蒸発し、気体になったり、逆に気体だった分子が凝縮して液化したりして、液体の量に変化が生じる。
これをしばらく放置しておくと、蒸発する分子の数と液化する分子の数が落ち着いて等しくなり、見かけ上液体に何の変化も起きていないような状態になる。これを気液平衡という。

この気液平衡時の蒸気の圧力のことを飽和蒸気圧という。
簡単にいうと液体分子が蒸発しようとする力(=蒸気が液化しようとする力)のことであり、いつ測定するかによって値が変わらないように、気液平衡時を基準として定義しているだけである。

温度が高くなればなるほど、分子の熱運動が激しくなるので、蒸発しようとする力も大きくなるため、当然飽和蒸気圧は大きくなる。
温度を高くし、どんどん蒸気圧が大きくなっていき、外圧と等しくなると、液体内部からも激しく蒸発が起こるようになる。これを沸騰といい、蒸発しようとする力が外から押さえつけてる力に勝るため激しく蒸発するということである。

図3

※水銀柱を用いた圧力表示

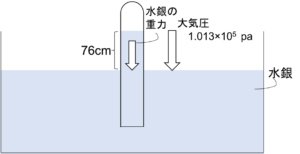
図4

圧力を測定する際に左図のような装置を使うことがある。水銀の入った容器中にガラス管を倒立されると、水銀がガラス管内に入りこみ、大気圧中では76cmの高さまで上ることが知られている。
これは容器の水銀の表面で大気圧による下向きの力と、ガラス管内の水銀の重力による下向きの力がつり合うためである。

水銀の密度を1.36×10⁵kg/m³とし、重力加速度を9.81m/s²とすると、76cmの水銀柱の圧力はガラス管の断面積S[m²]を用いて

\(S\times0.760\times10^{4}\times\frac{9.81}{S}=1.01\times10^{5}Pa \)

と算出され、確かに大気圧とつり合っている。そこで、外圧が未知な空間にこの装置を入れて、水銀柱が何cmまで上がるかを測定することで、同様の計算により圧力を算出することができる。この装置がよく知られていることから、1気圧を760mmHgと表すこともある。

ボイル・シャルルの法則

ボイルの法則

ボイルは実験により1662年、以下のボイルの法則を発見した。

〈ボイルの法則〉
温度が一定の時、気体の圧力pは気体の体積Vに反比例する。
すなわち、PV=（一定)

これは直観的にも分かりやすく、体積を2倍にすると、壁に衝突する気体分子の数は単位体積あたり半分になるので、圧力は1/2倍になりそうである。

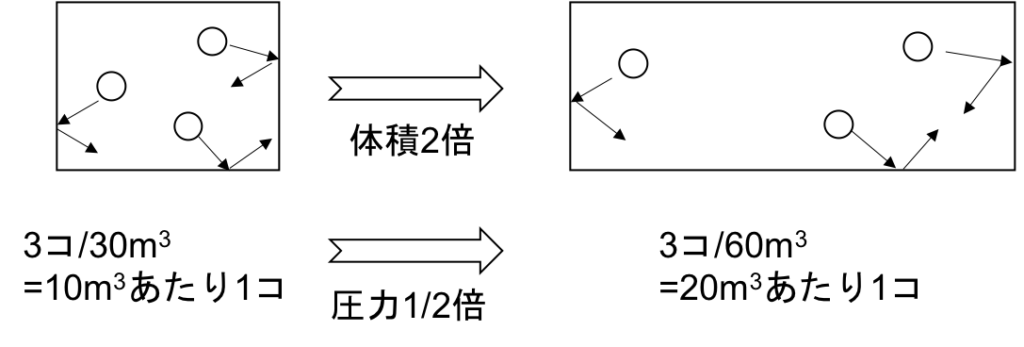
図5

Ex) 20℃、0×10³paで15Lを占める気体を、同温で体積を60Lにすると、
(PV=一定=)2.0×10³×15=□×60 ∴□=5.0×10²pa となる。

シャルルの法則

シャルルはその後1787年に以下のシャルルの法則を発見した。

〈シャルルの法則〉
圧力は一定の時、気体の体積Vは絶対温度Tに比例する。
すなわち、V = (定数) × T または　V/T = 一定

これは物理分野の気体分子運動論で確かめることができるが、直観的には温度を2倍にすると、熱運動の激しさが2倍になるので、気体が動き回る体積も2倍になりそうである。

ここで、絶対温度とは単位をK(ケルビン)とし、-273℃=0Kとする温度のことである。簡単にいうと、温度は粒子の熱運動の激しさをもとに定義したいので、全く粒子が運動をしない-273℃を基準の0とした温度系である。よってT[K]とt[℃]の間には　T[K] = t[℃] + 273℃ という関係式が成り立つ。

Ex) 27℃は300Kである。

ボイル・シャルルの法則

これら2つの法則をまとめて以下のようにボイル・シャルルの法則とされることが多い。

〈ボイル・シャルルの法則〉
気体の体積Vは圧力Pに反比例し、絶対温度Tに比例する。
すなわち、PV = (定数) × T または　PV/T = 一定

Ex) 0℃、01×10⁵paで22.4Lの気体は117℃、2.02×10⁵paで何Lになるか。

　　0℃は273K、117℃は390Kなので、ボイル・シャルルの法則より

\(\frac{1.01 \times 10^{5}\times 22.4}{273} = \frac{2.02\times10^{5}\times□}{390} \)

∴ □=16.0L

理想気体の状態方程式

ここで、気体のmol数を2倍、3倍…としていくと分子の数も2倍、3倍…と増えていくことから、気体の体積Vも2倍、3倍…と比例して増えていく。これをボイル・シャルルの法則と組み合わせ、　PV = (定数) × n × T (nはmol数)の形が導かれる。
いま、標準状態すなわち0℃(=273K)、1.013×10⁵paで1molの気体は22.4Lなので上式に代入することで比例定数を求めることができる。

\(1.013\times10^{5}\times22.4=□\times1\times273 \)

∴ □=8.31×10³ pa・L/mol・K

この比例定数を気体定数といい、Rで表す。これは一定なので

PV=nRT

という式を表すことができる。これを理想気体の状態方程式とよぶ。理想の意味は後ほど述べる。

※Rの値は単位により変わる。Vをリットルで表記するならR=8.31×10³pa・L/mol・Kだが、Vをm³で表記するとR=8.31J/K・molとなる。(∵ pa・m³ = J かつ1L = 10^-3m³)

Ex) 2.0molの気体を27℃で9Lにすると圧力は何paになるか
理想気体の状態方程式より
p×24.9 = 2.0×8.31×10³×300 ∴ p=2.0×10⁵pa
Ex2) 27℃、1.00×10⁵paで密度が1.2g/Lである気体の分子量は？
分子量をw g/molとすると、1Lあたり気体は1.2g= 1.2/w molなので
1.00×10⁵×1 = 1.2/w × 8.31×10³×300
∴ w≒30g/mol

ドルトンの分圧の法則

容器の中に複数種類の気体が入っている場合を考える。例えば、ある容器に気体Aがn_Amol、気体Bがn_Bmol入っているとする。このときAとBあわせた全体の気体としての圧力を全圧といい、気体Aが、その容器に入っていると考えた時のAの圧力を分圧という。(Bも同様)

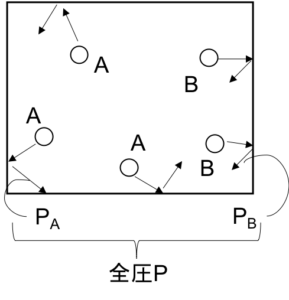
図6

この時、この混合気体の全圧Pは各気体の分圧P_A、P_Bの合計に等しい。

P = P_A + P_B

これをドルトンの分圧の法則という。
いま、気体Aにしても気体BにしてもV、R、Tは共通なので理想気体の状態方程式から

P_AV = n_ART …①
P_BV = n_BRT …②

の2式が成り立つ。
ここで、ドルトンの分圧の法則より①+②をすることで　PV=(n_A+n_B)RT…③が導かれる。いま、①と③を比べることにより、

\(P_{A}=P\times\frac{n_{A}}{n_{A}+n_{B}}\)、

同様に②と③から

\(P_{B}=P\times\frac{n_{B}}{n_{A}+n_{B}}\)

となる。
つまり、各分圧は全圧をmol比で比例配分してあげれば良い。(この\(\frac{n_{A}}{n_{A}+n_{B}}\)のようなmolでの割合をモル分率という。)

★同温同体積の混合気体では　分圧の比 = mol比
　同温同圧の　混合気体では　体積の比 = mol比　が成立する！

例題

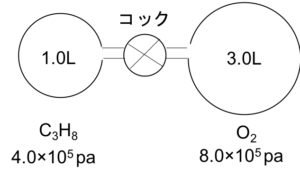
図a

図aのような耐圧容器にC₃H₈とO₂をそれぞれ示した圧力で入れた。
⑴コックを開くと、C₃H₈、O₂の分圧はそれぞれどうなるか？
⑵この混合気体に点火して完全燃焼させて温度を戻すと全圧はいくつ？
温度を一定に保ったまま、2.0×10⁵paのO₂3.0Lと1.0×10⁵paのN₂2.0Lをある容器に入れた。この混合気体の平均分子量を求めよ。(O:16、N:14)

【解答】

⑴C₃H₈は温度一定で体積が4倍になるのでPV=一定より圧力は1/4倍になる。　∴ C₃H₈の分圧：1.0×10⁵pa
O₂も同様に体積4/3倍より圧力は3/4倍になって　O₂の分圧：6.0×10⁵pa

⑵この混合気体に点火して完全燃焼させて温度を戻すと全圧はいくつ？
⑴より同温同体積なのでC₃H₈とO₂はmol比=分圧比なので、mol比は1:6である。(PV=nRTの内、VとTは一定なのでP∝nと考えてもよい。)
よって、表を以下のように立て、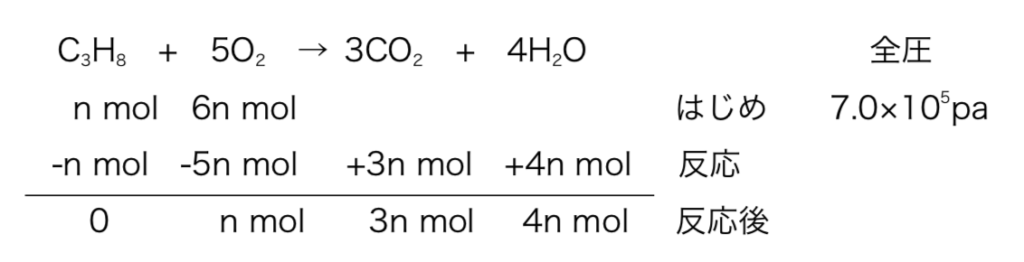
図7

反応前と反応後を比べ、VとTは一定で気体のmol数が4/7倍になっているため、(H₂Oは液体。)全圧も4/7倍になり、4.0×10⁵pa

※もちろん分圧に注目し、O₂のmol数が1/6倍よりO₂の分圧も1/6倍として求めてもよい。
状態方程式をO₂、N₂それぞれにつきたてると
2.0×10⁵×3.0 = n_O2×R×T
1.0×10⁵×2.0 = n_N2×R×T
となるため、O₂とN₂のmol比はN_O2:N_N2 = 3:1と求まる。
∴ 32 × 3/4 + 28 × 1/4 = 31

→mol比=分圧の比などではないが、気体の問題は　PV=nRTをたてるとだいたい解決するのでオススメ。mol比=分圧比も覚えなくとも導ける。

実在気体と圧縮因子

実は⑸までで議論していたPV=nRT他はすべて理想気体を呼ばれるとても特別な条件を仮定した気体しか成り立たず、現実の気体=実在気体では、より慎重な議論が必要となる。

　実はそもそも理想気体では、以下の2つの条件を仮定していた。

分子間力ははたらかず自由に分子が動けるものとする。
分子自身の大きさを考えず、容器内すべてを分子が動けるものとする。

分子間力の影響

分子と分子は分子間力(ファンデルワールス力など)によって引きつけ合っているので、実在気体での圧力はPは、理想気体での圧力より小さくなる。

分子自身の大きさの影響

分子を球として考えると、左図の長方形の容器の内、色付き部分を分子の重心が動くことは出来ない。
そのため実在気体が占める体積は理想気体で考えていた体積より大きくなる。

図8

発展

よって①、②を考慮してPやVに補正項を加えて

\((P+\frac{an^{2}}{V^{2}})(V+nb)=nRT\)(a、bは気体に依存する定数)

が実在気体において成立する。これをファンデルワールスの状態方程式という。

理想気体と実在気体を比較するために、\(\frac{PV}{nRT}\)の値(=圧縮因子という。Zで表す。)を考えてみる。
理想気体ではZは常に1なので、1からどれくらいずれているかが指標になる。

温度ごとの比較

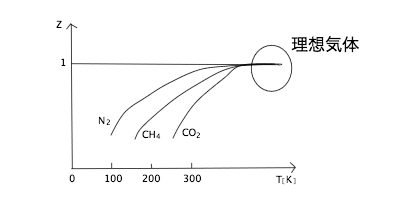
図9

温度は高温になればなるほど理想気体に近づいていく。
これは低温であればあるほど分子の熱運動が穏やかで、分子同士が分子間力でひかれ合う影響が大きくなるからである。その結果、 Pが小さくなりZ<1。

一方、高温にすると分子間力を振り切って激しく熱運動するので、分子間力の影響を無視しやすくなる。
圧力ごとの比較

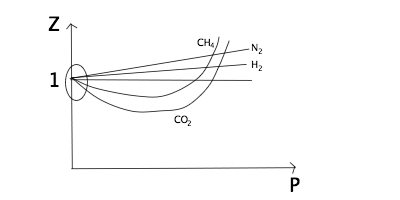
図10

圧力は基本的には低圧の方が理想気体に近い。
低圧条件では分子同士は抑えつけられておらず互いに程よく離れているので分子間力や分子の大きさを無視しやすいからである。
ただし、その中でもCO₂などの分子内にC^δ+– O^δ-のように極性をもつものは比較的大きな分子間力がはたらくことから、Zが1を大きく下回りやすい。

一方、高圧にしてくとどんどん分子同士が近づいていき、接触するほどになると今度は分子自身の大きさゆえにそれ以上近づけないという、分子自身の大きさによる影響が大きくなっていく。
それにより、Vが大きくなる作用でZが1を超えていく。