ここでは 束縛条件について述べる．「束縛条件」という言葉は，高校の教科書ではあらわに登場しないかもしれないが，大学受験の物理でも使う概念である．
そのため，ここでは敢えて束縛条件という言葉を用いる．そうすることで，その存在を認識でき，その理解に繋がると考えている．この記事では運動方程式を用いる．まだ運動方程式を用いてどのように運動を決定するかについてはまだ詳しく述べていないが，既に紹介した\(ma = F\) だけ知っていれば問題ない．運動の決定についてはまた別の記事で説明する．
この束縛条件というのは，その名の通り物体の運動を束縛するような条件である．参考書によっては「拘束条件」と書かれることもある．ここではいくつかの具体的な例を見ながら，束縛条件とはどのようなものか，そして問題を解くにあたってどのように用いるものなのかを説明する．
「公式のない力」の決定 束縛条件
以前の記事で，「公式のない力は，束縛条件から求める」ということを述べたが，その具体的な話には言及しなかった．ここでは束縛条件を用いて，実際に公式のない力の決定を行う．
まず束縛条件が数式上，どのような「条件」(あるいは制限と言っても良いだろう) を与えるかを簡潔に述べる．束縛条件は，物体の加速度に対する制限である．加速度の積分を繰り返すことで，速度や変位が求まることは既に述べた．加速度に制限が加わるということは，物体の運動を制限，すなわち束縛することに等しい．
これから具体的な例を見ながら，束縛条件が加速度に制限を与えることを理解しよう．そして加速度が制限を受けることで，「公式のない力」が求まることが分かるはずである．
例題1
以下の図1 のように，変形しない物体の上に，質量\(m\)の物体がある．この物体が床から受ける垂直抗力の大きさ\(N\)を求めよ．
解答と解説
このような簡単な問題であれば，すぐに答えられる人も多いだろう．重要なことは，問題が解けることではなく，束縛条件を用いていると認識することである．
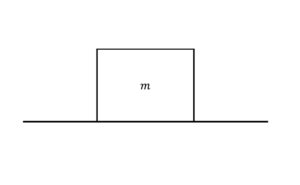図1: へこまない床の上の物体
ここでの束縛条件は，「床が変形しない」ということである．当たり前だと思う人も多いかもしれないが，この条件がなければ垂直抗力を決定できない．具体的には，床が変形しないことから，床に垂直は方向の加速度は0 である．つまり運動方程式は，
\(m\cdot 0 = N-mg\) (1)である．これにより，求める垂直抗力は
\(N = mg\) (2)である．
加速度が0 であるということを強調して書いた．もし床が変形しうるなら，物体は鉛直方向にも運動をするので，加速度を0 とすることはできない．このように「物体が鉛直方向に物体が動かない」ように束縛されているのである．
例題2
以下の図2 のように，伸び縮みしないひもに，質量\(m\)の物体が吊るされている．この物体がひもから受ける張力の大きさ\(T\)を求めよ．
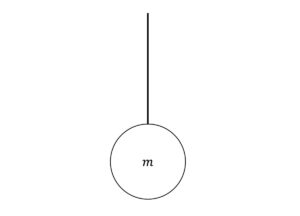図2: 伸び縮みしないひもに吊るされた物体
解答と解説
この問題についても，多くの人がすぐに解くことができるだろう．ただこれも先程と同様に，束縛条件を考える．今回の束縛条件は「ひもが伸び縮みしない」ことである．ひもが伸び縮みしないので，物体の鉛直方向の加速度は0 である．またもや加速度に制限が付いた．これにより運動方程式は，
\(m\cdot 0 = T-mg\) (3)となるから，求める張力\(T\)は，
\(T = mg\) (4)である．
例題3
以下の図3 のように，床から角度\(\theta\)だけ傾いた粗い斜面上に，質量\(m\)の物体が静止している．物体が斜面から受ける摩擦力の大きさ\(f\) を求めよ．尚，斜面は変形しないものとする．
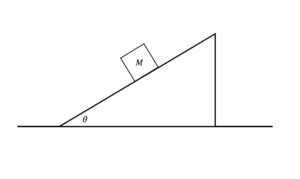図3: 斜面上で静止している物体
解答と解説
この問題を見て，「問題文中に摩擦係数がない」，あるいは「垂直抗力を求めよう」と思った人は待って欲しい．以前の力の記事で摩擦力について見たことを思い出そう．動摩擦力，最大摩擦力は公式のある力だが，静止摩擦力には公式がないのだった．
この問題で，問われている摩擦力が動摩擦力だと思う人はいないだろう．「問題文中に摩擦係数がない」，あるいは「垂直抗力を求めよう」と思った人は最大摩擦力と勘違いしているのである．
もちろん今，物体が受けている摩擦力が最大になっている可能性もあるが，それは静止摩擦力の特別な場合に過ぎない．またこの問題は静止摩擦係数がなくても解ける．
今回の束縛条件も，斜面が変形しないことから，物体の斜面方向の加速度が0 ということを用いる．もちろん，斜面に垂直な方向の加速度も0 で，それを用いると垂直抗力が求まる．今回問われているのが，摩擦力なので斜面方向にのみ着目する．運動方程式は，
\(m\cdot 0 = mg\sin \theta -f\) (5)ゆえ，求める摩擦力は，
\(f = mg\sin \theta\) (6)である．
最後に
登録6000人以上！
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中！
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント！
登録及び登録解除も簡単ですので、お気軽にご登録ください。
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。
